Mathematical Modeling of Vegetation Heterogeneity and Complex Topography Effects on Turbulent Exchange of GHG within the Atmospheric Surface Layer †
Abstract
1. Introduction
2. Materials and Methods
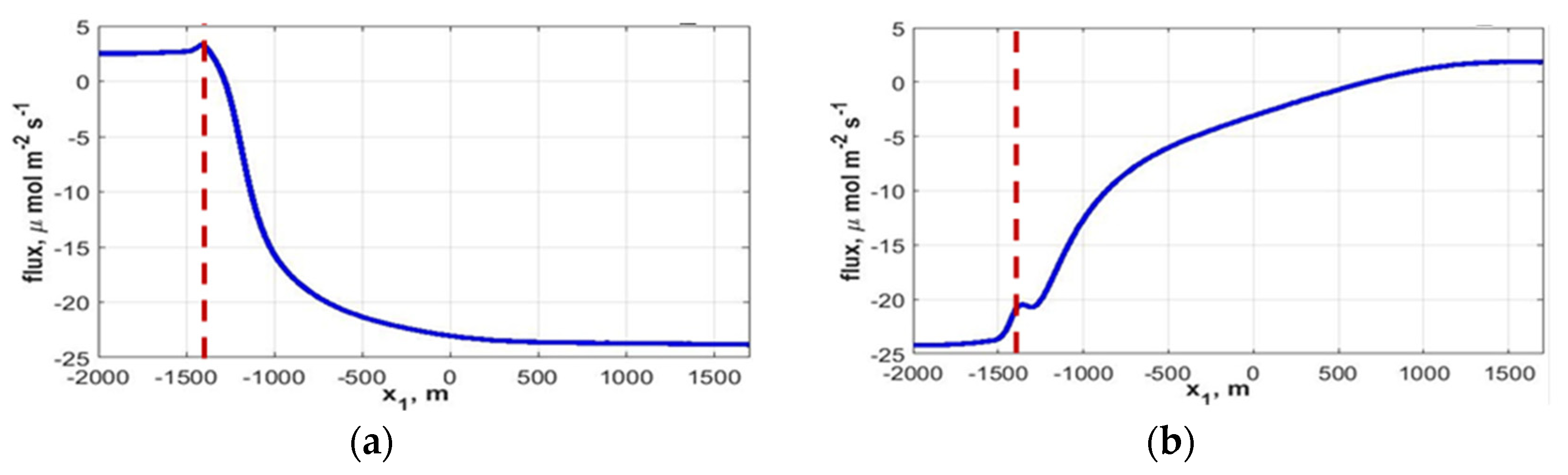
3. Results
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Oltchev, A.; Cermak, J.; Nadezhdina, N.; Tatarinov, F.; Tishenko, A.; Ibrom, A.; Gravenhorst, G. Transpiration of a mixed forest stand: Field measurements and simulation using SVAT models. Boreal Environ. Res. 2002, 7, 389–397. [Google Scholar]
- Zhang, G.; Thomas, C.; Leclerc, M.Y.; Karipot, A.; Gholz, H.L.; Binford, M.; Foken, T. On the effect of clearcuts on turbulence structure above a forest canopy. Theor. Appl. Climatol. 2007, 88, 133–137. [Google Scholar] [CrossRef]
- Burba, G. Eddy Covariance Method for Scientific, Industrial, Agricultural and Regulatory Applications: A Field Book on Measuring Ecosystem Gas Exchange and Areal Emission Rates; LI-COR Biosciences: Lincoln, NE, USA, 2013. [Google Scholar]
- Sogachev, A.; Panferov, O. Modification of two-equation models to account for plant drag. Bound. Lay. Meteorol. 2006, 121, 229–266. [Google Scholar] [CrossRef]
- Mukhartova, Y.V.; Levashova, N.T.; Olchev, A.V.; Shapkina, N.E. Application of a 2D model for describing the turbulent transfer of CO2 in a spatially heterogeneous vegetation cover. Moscow Univ. Phys. Bull. 2015, 70, 14–21. [Google Scholar] [CrossRef]
- Mamkin, V.; Kurbatova, J.; Avilov, V.; Mukhartova, Y.; Krupenko, A.; Ivanov, D.; Levashova, N.; Olchev, A. Changes in net ecosystem exchange of CO2, latent and sensible heat fluxes in a recently clear-cut spruce forest in western Russia: Results from an experimental and modeling analysis. Environ. Res. Lett. 2016, 11, 125012. [Google Scholar] [CrossRef]
- Mukhartova, Y.V.; Krupenko, A.S.; Mangura, P.A.; Levashova, N.T. A two-dimensional hydrodynamic model of turbulent transfer of CO2 and H2O over a heterogeneous land surface. IOP Conf. Ser. Earth Environ. Sci. 2017, 107, 012103. [Google Scholar] [CrossRef]
- Sogachev, A.; Kelly, M.; Leclerc, M.Y. Consistent two-equation closure modeling for atmospheric research: Buoyancy and vegetation implementations. Bound. Lay. Meteorol. 2012, 117, 307–327. [Google Scholar] [CrossRef]
- Mukhartova, Y.V.; Mangura, P.A.; Levashova, N.T.; Olchev, A.V. Selection of boundary conditions for modeling the turbulent exchange process within the atmospheric surface layer. Comput. Res. Model. 2018, 10, 27–46. [Google Scholar] [CrossRef][Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukhartova, I.; Krupenko, A.; Mangura, P.; Olchev, A. Mathematical Modeling of Vegetation Heterogeneity and Complex Topography Effects on Turbulent Exchange of GHG within the Atmospheric Surface Layer. Proceedings 2018, 2, 1310. https://doi.org/10.3390/proceedings2201310
Mukhartova I, Krupenko A, Mangura P, Olchev A. Mathematical Modeling of Vegetation Heterogeneity and Complex Topography Effects on Turbulent Exchange of GHG within the Atmospheric Surface Layer. Proceedings. 2018; 2(20):1310. https://doi.org/10.3390/proceedings2201310
Chicago/Turabian StyleMukhartova, Iuliia, Alexander Krupenko, Polina Mangura, and Alexander Olchev. 2018. "Mathematical Modeling of Vegetation Heterogeneity and Complex Topography Effects on Turbulent Exchange of GHG within the Atmospheric Surface Layer" Proceedings 2, no. 20: 1310. https://doi.org/10.3390/proceedings2201310
APA StyleMukhartova, I., Krupenko, A., Mangura, P., & Olchev, A. (2018). Mathematical Modeling of Vegetation Heterogeneity and Complex Topography Effects on Turbulent Exchange of GHG within the Atmospheric Surface Layer. Proceedings, 2(20), 1310. https://doi.org/10.3390/proceedings2201310




