Improved 3-Phase Current Transducer ^†

Abstract

We propose improved contactless DC/AC current transducer for 3-phase current lines based on 8 integrated fluxgate sensors. Using proper processing we ideally achieve a complete suppression of external homogeneous fields, and field gradients up to the 4th order. The sensitivity to external currents (crosstalk) is improved 15-times compared to [1]. The usage of micro fluxgate sensors instead of magnetoresistive sensors improves the temperature stability: the sensitivity temperature coefficient was reduced from 0.3%/K to 50 ppm/K and offset drift was reduced from 50 mA/K to 1 mA/K.

1. Introduction

Smart grids need precise information of electric current including its DC component. Lightweight transducers which can be mounted to the existing power lines are required. Magnetic cores and yokes are too heavy. While Rogowski coils cannot measure DC component and they have limited frequency range, yokeless magnetic sensors have good potential for this application [2]. Circular or rectangular multisensor arrays closely approximate the Ampere’s law and therefore they effectively suppress the external currents [3]. Their disadvantage that they need large number of sensors, at least 8 per phase.

2. Description of Measurement Methods

Three-phase overhead power lines consist of three bare conductors, each of which carries sinusoidal current shifted by 120°. In this paper we assume linear arrangement with pitch d = 30 cm. Current measurement by clamp-on magnetic sensor arrays is a suitable method for this application, as it provides galvanic isolation, low weight and power consumption low enough for wireless operation.

2.1. Sensors Placed Symmetrically around Conductors

The simplest configuration uses two sensors at each wire, placed symmetrically left and right at distance r = 20 mm (as in Figure 1a). Differential measurement eliminates the influence of homogeneous field (e.g., Earth’s field). Crosstalk from other two phases is not compensated, and its value is

(1)

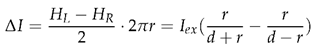
2.2. Gradiometric Arrangement

More elaborate approach was presented in [1], which uses pairs of closely spaced sensors (Figure 1b) to obtain the gradient of H, which is then used to reconstruct values of phase currents, while greatly increasing rejection of field from other phases and external sources. Our simulation however did not confirm any improvement over naïve case from Section 2.1. The problem of this method is that by calculating differences H₁ − H₂ we lose half of the information from the sensors.

2.3. Method with Polynomial Estimation

The same arrangement from Figure 1a is used. From the readings of six sensors we can calculate three unknown phase currents and position and amplitude of one external current. If the currents are DC, we have 6 independent equations, in AC case we have 6 equations for instantaneous values or 6 equations for amplitude and 6 for phase. However we cannot expect that the external current is only one and we should expect also external fields of other origin such as ferromagnetic objects which can also distort the field from external current. We therefore decided to find solution which nulls external field in y direction and its gradients up to second order. Fields in x direction do not affect the sensors at all. We therefore suppose that the field at each sensor consists of three contributions from phase currents, and from the external field with unknown distribution:

(2)

External field H_ext may have any spatial distribution, which we approximate with second or fourth degree polynomial (depending of sensor count). Six sensors produce six different equations [2]. A linear system is formed:

(3)

Solving this matrix equation provides all currents and 1-D estimation of external field at the same time. However simulations show that second order polynomial is difficult to fit onto 1/d distribution (which is the case in single external conductor). As a result the improvement over the gradiometric method is only mild. For this reason the number of sensors was increased to allow estimating up to 4th order. Two additional sensors are placed halfway between phase conductors (Figure 1a).

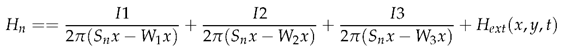
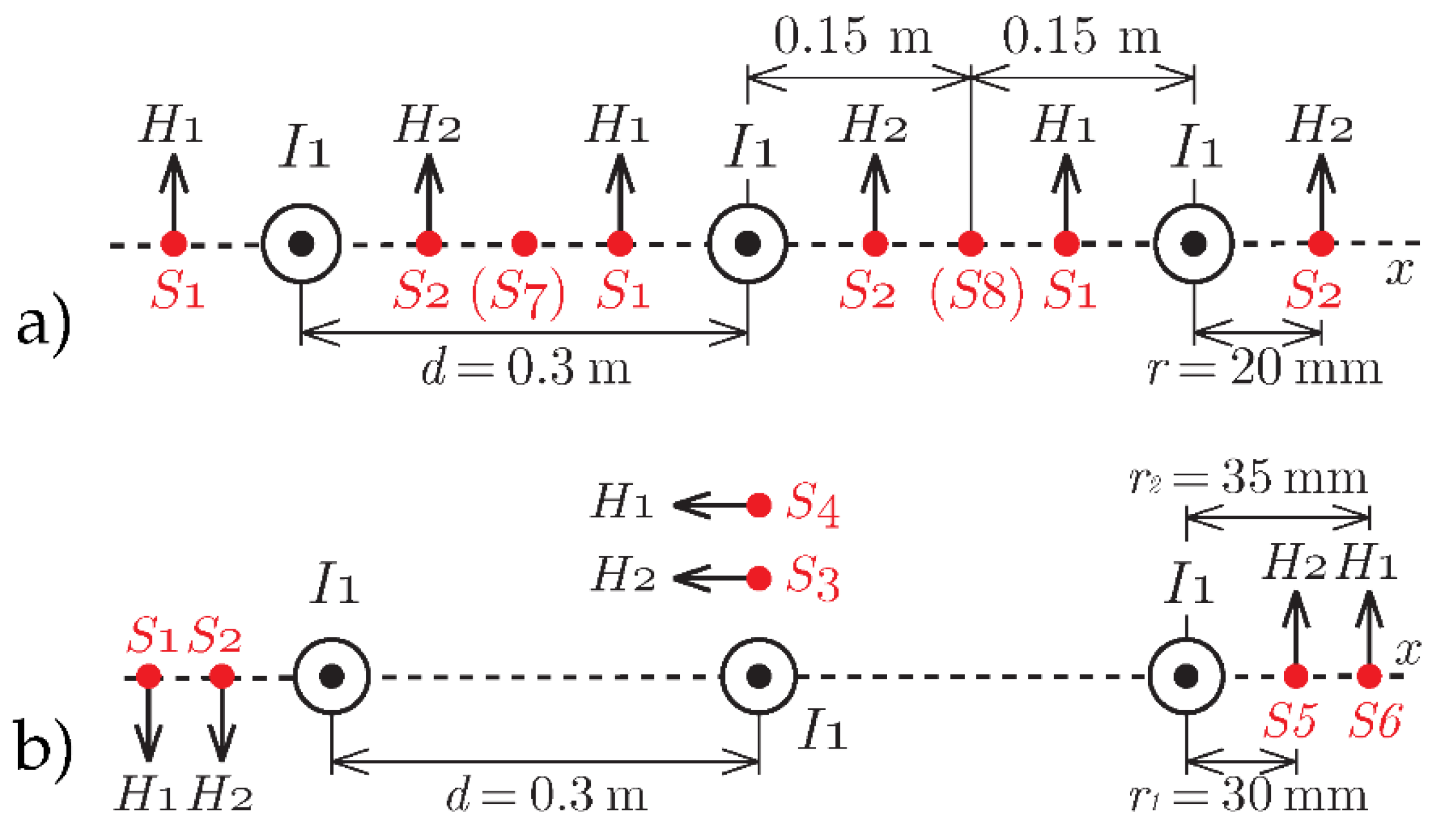
3. Measurement Setup

Measurement was done with a 50 Hz three-phase transformer feeding Y-connected resistors with 5 A RMS. Length of conductors’ straight section was 4.4 m. Wooden beam with sensors was placed on non-magnetic tripods across the wires near their center (Figure 2). Fluxgate sensor ICs TI DRV425 were used, mounted on a PCB to locate them precisely at 20 mm from measured conductor (Figure 3). External current was generated by another transformer and was also set to 5 A. Output from the magnetic sensors, together with current measured by shunt resistors, was captured by an NI USB interface card at 5000 SPS. Data processing was done offline on 10 periods of measured current.

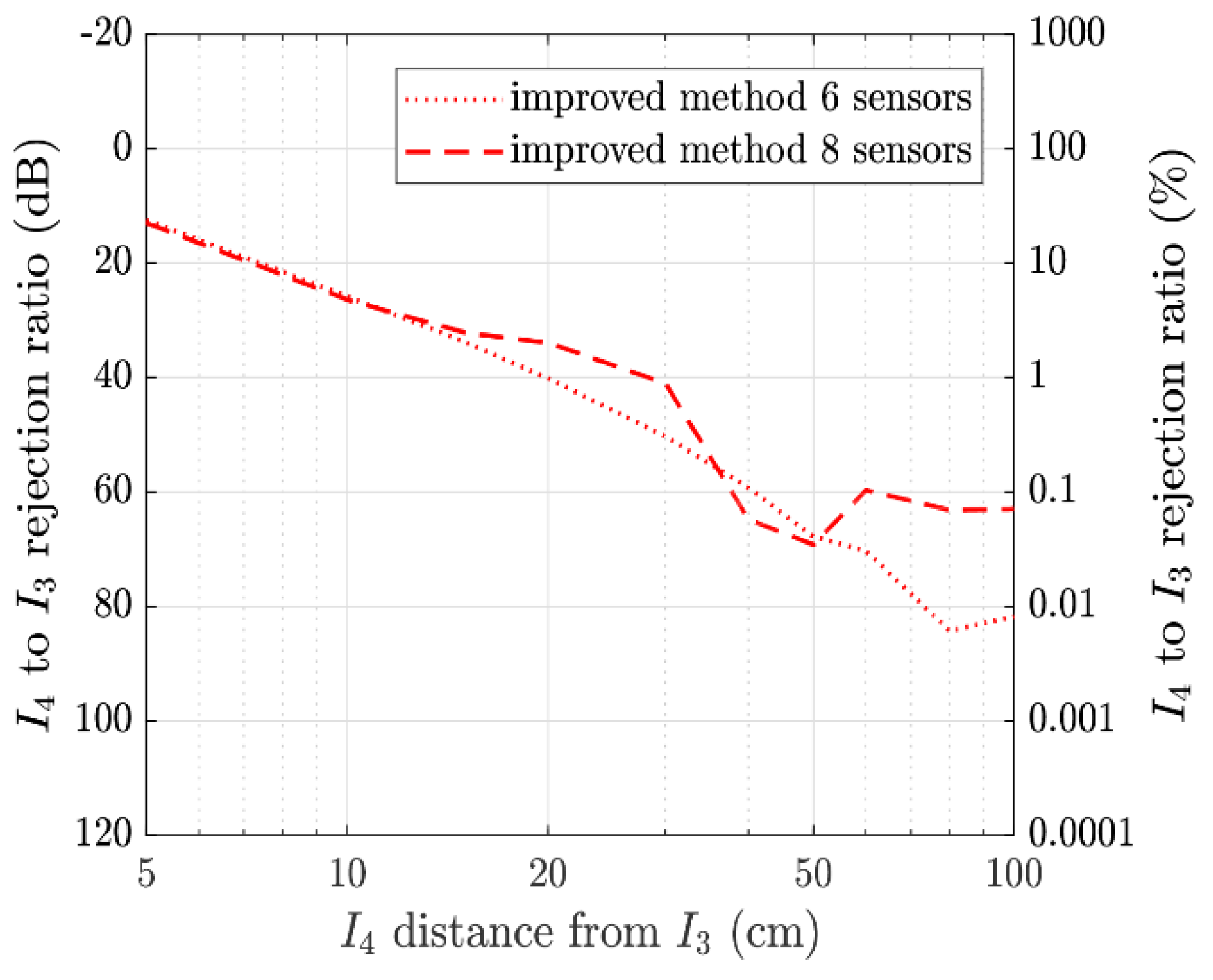
4. Results of Simulation and Measurement

Six-sensor arrangement with polynomial estimation in theory provides results better than gradient method, however our setup was limited to configuration from Figure 1b, and therefore we could not do direct comparison with [1]. When comparing results of simulation, our new method of polynomial estimation provides advantage over both simple (Section 2.1) and gradient (Section 2.2) method. Figure 4 summarizes the theoretical performance of each method. Measurement with setup described in Section 3 was conducted, yielding results in Figure 5. Non-ideal sensor placement and external disturbances cause the characteristics to deviate from theory, particularly for larger distances.

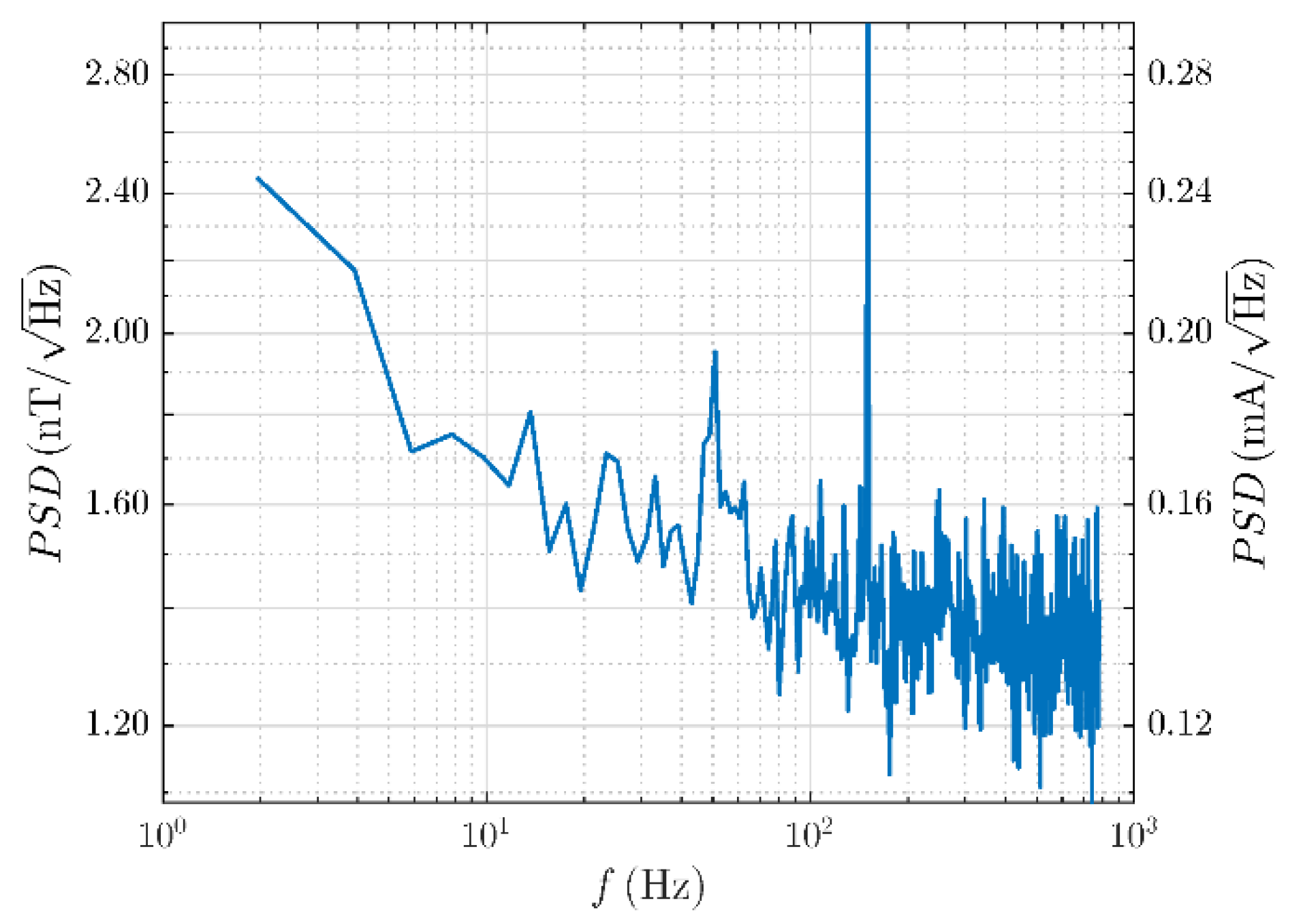
5. Effects of Sensor Noise and Temperature Stability

Sensor noise was measured with a SR770 network analyzer and three-layer permalloy shield at room temperature. Noise spectrum (Figure 6) is almost white, from zero to 1 kHz the total noise current is around 6 mA. This is similar value which can be achieved with the best AMR sensors. The main advantage of using fluxgate is its better temperature stability. By using fluxgate instead of AMR the sensitivity temperature coefficient was reduced from 0.3%/K to 50 ppm/K and offset drift was reduced from 50 mA/K to 1 mA/K.

6. Discussion

We propose improved contactless DC/AC current transducer for 3-phase current lines based on integrated fluxgate sensors. Using proper processing of 6 sensors we ideally achieve a complete suppression of external homogeneous fields, first and second order gradients and compensation of the crosstalk between the phases. However the sensitivity to the external currents (crosstalk error) is only mildly improved from the results in [1]. Dramatic improvement can be achieved by increasing the number of sensors to 8, which allows suppression of all gradients up to 4th order and reduces the crosstalk error 15-times. The usage of micro fluxgate sensors instead of magnetoresistive sensors additionally improves the temperature stability: the sensitivity temperature coefficient was reduced from 0.3%/K to 50 ppm/K and offset drift was reduced from 50 mA/K to 1 mA/K. The developed equations were verified by simulation and measurement.