Abstract
Classical linear regression has been used to measure the relationship between rainfall data and altitude in different meteorological stations, in order to evaluate a linear relation. The values of rainfall are supposed as dependent variables and the values of elevation of each station as independent variables. It has long been known that a classical statistical relationship exists between annual rainfall and the station elevation which in many cases is linear as the one examined in this article. However classical linear regression makes rigid assumptions about the statistical properties of the model, accepting the error terms as random variables, and the violation of this assumption could affect the validity of the classical linear regression. Fuzzy regression assumes ambiguous and imprecise parameters and data. For this reason it may be more effective than classical regression. In this paper we evaluate the relationship between annual rainfall data and the elevation of each station in Thessaly’s meteorological stations, using fuzzy linear regression with trapezoidal membership functions. In this possibilistic model the dependent measured elevations are crisp, and the independent observed rainfall values as well as the parameters of the model are fuzzy.
1. Introduction
The scope of constructing in engineering a model is always to attempt to maximize its usefulness. This aim is closely connected with the relationship among three key characteristics of every systems model: complexity, credibility, and uncertainty. Our purpose in systems modelling is to estimate an optimal level of uncertainty for each modelling problem. In 1965 Zadeh in [1], introduced the theory of fuzzy sets, in which the fuzziness of a system incorporated all the types of uncertainty, in contrast with probability theory, which was capable of representing only one of several distinct types of uncertainty.
In Hydrology, rainfall measurement models have been extensively used in the design process of water resource projects such as hydrological prediction, spillway design, climatic change studies, rainfall and runoff correlation etc. Rainfall measurements in a specific area are commonly displayed in the form of time series, where recorded values can be either continuous or discrete. In many instances, there is a correlation between rainfall data that belong to different stations and comprise measurements with differing range and stations elevations. Correlation analysis is used to depict the relation between the independent variable (usually the meteorological station elevations) and the dependent variables (meteorological stations rainfall data).
In classical linear regression, the difference between measurement values and estimated values, is a random variable with normal distribution and is considered to be caused by measurement errors. Upper and lower bounds of the estimated value are calculated and the probability that the estimated value will lie between them represents the estimation confidence. According to this, classical regression is considered to be probabilistic and has many uses, but can be rendered problematic if the data set is small, if it’s hard to prove that error distribution is normal, if there is fuzziness between dependent and independent variables or if linearity acceptance is not proper [2].
Nowadays, new regression models have been introduced, based on fuzzy logic [3,4,5,6,7,8,9,10,11,12,13]. In fuzzy regression the difference between measurement values and estimated values is attributed to the inherent fuzziness of the system as well as to the fuzziness of input and output data. In contrast with classical regression analysis, fuzzy regression analysis uses fuzzy functions for the regression factors and usually meets one of the three cases: (a) Crisp input values and crisp output values (CICO); (b) Crisp input values and fuzzy output values (CIFO); and (c) Fuzzy input values and fuzzy output values (FIFO). In all of these three cases, estimated values are fuzzy.
Most of the cited above writers have used tridiagonal fuzzy functions for the formulation of the problem. However the need to use trapezoidal functions, results of the following reasons [14]: (a) we need to optimize the fuzziness of the model and (b) we need to restrict experimental data inside the estimated value range. Using trapezoidal membership functions for estimated values [14,15,16,17,18] allows us to achieve inclusion for output data with triangular membership functions and estimated values with trapezoidal membership functions , for confidence level h = 1, for which the kernel is not minimized in a point: . In addition, for a level of confidence h = 0, we can achieve inclusion: . Due to the linearity of the membership function, inclusion for those levels of confidence, allows us to ensure that inclusion is possible for every level of confidence: . Consequently, trapezoidal fuzzy parameters have higher capability to model varieties of fuzziness than triangular fuzzy parameters.
Trapezoidal membership function models have been used by [14,15,19,20,21,22,23,24]. Charfeddine in [19] extended Tanaka’s method for the case of trapezoidal membership functions with crisp measured input and output values. She used a fuzzy level function , with four crisp level functions For, , she used Tanaka’s method [8], whereas for , she used classical linear regression, which led to function and standard deviation σ of the model. Based on this , become: with being an adjustment factor. Ganesan and Veeramani in [22], described a fuzzy linear programming with symmetric trapezoidal fuzzy parameters. They proved fuzzy analogues of some important theorems of linear programming and they gave a numerical example, leading to a solution of fuzzy linear programming problems. Fung et al. in [25], proposed a new model for asymmetric trapezoidal fuzzy parameters. Kumar and Kaur in [24] presented a new method, called Mehar’s method, suitable for solving fuzzy linear programming problems with trapezoidal fuzzy parameters. They proved that this method is easy to apply to fuzzy linear programming problems, with respect to existing methods. Kheirfam and Verdegay in [23] extended the dual simplex method to fuzzy linear programming, with symmetric trapezoidal fuzzy parameters. They studied the variation of values to a certain limit, so that the fuzzy optimal solution remains invariant.
In this article, a possibilistic model (Tzimopoulos et al. model) is described, where membership functions are trapezoidal, measured input values are crisp and measured output values are fuzzy triangular [13]. In this model, a rather simple two-phase method was used, with one crisp measured input value and one fuzzy measured output value. During step 1, measured input and output values were considered crisp, while parameters were considered fuzzy and supports were estimated using Tanaka’s method. In step 2, estimated supports were considered to be the known kernel of the trapezoidal membership functions and in the inclusion they were transferred to the known terms. Supports for the trapezoidal membership functions of the estimation were calculated. Triangular membership functions were used for measured output values.
Further, we present one application of the above model, concerning a hydrological problem in the region of Central Thessaly (Greece), where twenty rainfall measurement stations of the region with rainfall data and their elevation have been used.
2. Mathematical Model
2.1. Model of Tzimopoulos et al. (2006)
2.1.1. Generalities
Measured input values are considered crisp and measured output values are considered symmetrical triangular fuzzy numbers (Figure 1), while estimated values are considered trapezoidal fuzzy numbers (Figure 2). The above problem can be divided into the following two steps:
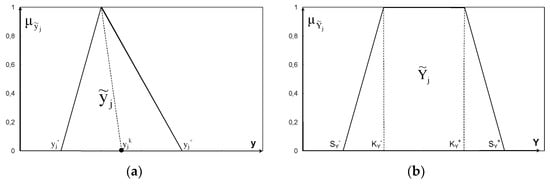
Figure 1.
(a) Triangular membership function, (b) Trapezoidal membership function.
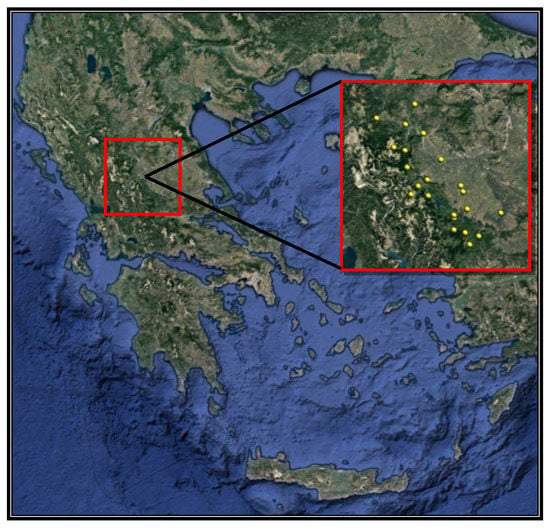
Figure 2.
Central Thessaly meteorological stations.
2.1.2. Step 1
According to the kernel inclusion constraint mentioned above, we have:
Namely, the kernel of experimental output values is within the kernel of estimated values. According to Shapiro et al. (2009), for the case of crisp output values (only the kernels of measured values), if we apply Tanaka’s method (Tanaka 1987), the range encircles the kernels of experimental values. In this stage, only triangular functions are applied for the method of Tanaka and the possibilistic model used is: . Thus, the problem of determining the estimated values in this step is:
Through the solution of this system we get the surroundings as follows:
As long as they meet the same constraints, these surroundings coincide with the kernel of trapezoidal functions, resulting in the relations below:
2.1.3. Step 2
We apply now support inclusion:
where space is given as follows:
Based on relations (3a, 3b, 3c) and (4a, 4b), we get:
where and are known since they have been calculated during step 1.
The problem turns now into the following:
s.t
3. Applications
3.1. Generalities
Given the following rainfall and elevation data of twenty meteorological stations of central Thessaly (Greece) (Table 1 and Table 2), with crisp input data and symmetric output fuzzy data, we want to assess the two step model of Tzimopoulos et al., using the fuzzy regression method, considering trapezoidal membership functions for the assessment.

Table 1.
Elevation and Rainfall data from meteorological stations of Central Thessaly.

Table 2.
Elevation and Rainfall data from meteorological stations of Central Thessaly.
3.2. Step 1
We apply Tanaka’s model, considering that output data are crisp. For, the model is written as follows:
s.t
Solving this problem we get kernel equations:
3.3. Step 2
In phase 2, the kernel is considered to be known and the model is written as follows:
s.t
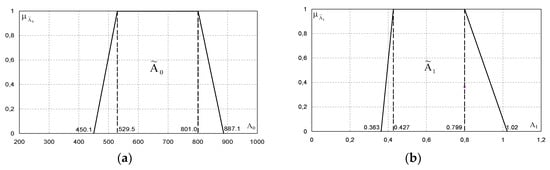
Figure 3.
(a) Predicted parameters , (b) Predicted parameters .
In the Figure 4a illustrates the estimated output data, Figure 4b illustrates the measured and predicted values at Megali_Kerasia_Ypex meteorological station, while Figure 3a, b illustrate the predicted parameters and respectively.
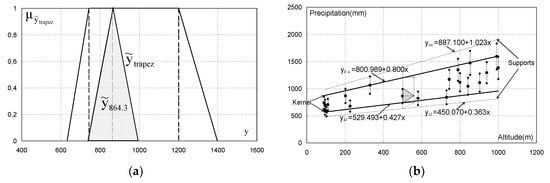
Figure 4.
(a) Estimated fuzzy output data, (b) Measured and predicted output at Meg._Ker._Ypex station.
4. Comments-Conclusions
The two-step model has the advantage of using only four unknown quantities during each phase, in contrast with Bisserier and Fung models, which use eight.
In all the above cases, the presented model can be applied for all confidence levels and have the following property: data kernels are included into estimated kernels and data supports are also included into estimated supports.
In the case of rainfall measurement observations, station association is achieved, even for small samples and we can extend the shorter time series, due to fuzzy correlation for more rainfall stations.
References
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Savic, D.A.; Pedrycz, W. Evaluation of fuzzy linear regression models. Fuzzy Sets Syst. 1991, 39, 51–63. [Google Scholar] [CrossRef]
- Papadopoulos, B.; Sirpi, M. Similarities in Fuzzy Regression Models. J. Optim. Theory Appl. 1999, 102, 373–383. [Google Scholar] [CrossRef]
- Papadopoulos, B.; Sirpi, M. Similarities and Distances in Fuzzy Regression Models. Soft Comput. 2004, 8, 556–561. [Google Scholar] [CrossRef]
- Redden, D.T.; Woodall, W.H. Further examination of fuzzy linear regression. Fuzzy Sets Syst. 1996, 79, 203–211. [Google Scholar] [CrossRef]
- Shapiro, A.F.; Berry-Stölzle, T.R.; Koissi, M.-C. The Fuzziness in Regression Models. ARC2009_Shapiro_06 PDF. 2009; p. 6.
- Tanaka, H.; Uejima, S.; Asai, K. Linear regression analysis with fuzzy models. IEEE Trans. Syst. Man Cybern. 1982, 12, 903–907. [Google Scholar]
- Tanaka, H. Fuzzy data analysis by possibilistic linear models. Fuzzy Sets Syst. 1987, 24, 363–375. [Google Scholar] [CrossRef]
- Tanaka, H.; Watada, J. Possibilistic linear systems and their application to the linear regression model. Fuzzy Sets Syst. 1988, 27, 275–289. [Google Scholar] [CrossRef]
- Tanaka, H.; Hayashi, I.; Watada, J. Possibilistic linear regression analysis for fuzzy data. EJOR 1989, 40, 389–396. [Google Scholar] [CrossRef]
- Tanaka, H.; Ishibuchi, H. Identification of possibilistic linear systems by quadratic membership functions of fuzzy parameters. Fuzzy Sets Syst. 1991, 41, 145–160. [Google Scholar] [CrossRef]
- Tzimopoulos, C.; Papadopoulos, Β. Fuzzy Logic with Application in Engineering; Ziti: Thessaloniki, Greece, 2013; 627p. (In Greek) [Google Scholar]
- Tzimopoulos, C.; Papadopoulos, K.; Papadopoulos, B. Fuzzy Regression with Applications in Hydrology. IJEIT 2016, 5, 69–75. [Google Scholar]
- Bisserier, A. Une approche Paramétrique de la Régression Linéaire Floue-Formalisation par Intervalles. Ph.D. Thesis, Université de Savoie, Chambéry, France, 2010. [Google Scholar]
- Bisserier, A.; Boukezzoula, R.; Galichet, S. Linear Fuzzy Regression Using Trapezoidal Fuzzy Intervals. In Proceedings of the IPMU’08, Torremolinos, Spain, 22–27 June 2008; pp. 181–188. [Google Scholar]
- Bisserier, A.; Boukezzoula, R.; Galichet, S. Linear Fuzzy Regression Using Trapezoidal Fuzzy Intervals. JUS 2010, 4, 59–72. [Google Scholar]
- Bisserier, A.; Boukezzoula, R.; Galichet, S. A revisited approach to linear fuzzy regression using trapezoidal fuzzy intervals. Inf. Sci. 2010, 180, 3653–3673. [Google Scholar] [CrossRef]
- Bisserier, A.; Boukezzoula, R.; Galichet, S. Linear Fuzzy Regression Using Trapezoidal Fuzzy Intervals. In Foundations of Reasoning under Uncertainty; Bouchon-Meunier, B., Magdalena, L., Ojeda-Aciego, M., Verdegay, J.L., Yager, R., Eds.; Springer: Berlin, Germany, 2010; Volume 249, pp. 2–22. [Google Scholar]
- Charfeddine, S. Optimisation de l’ offre d’ une Compagnie Aérienne en Environnement Incertain. Thèse de Docteur; Université de Toulouse: Toulouse, France, 2004. [Google Scholar]
- Charfeddine, S.; Mora-Camino, F.; De Coligny, M. Fuzzy linear regression: Application to the estimation of air transport demand. In Proceedings of the International Conference on Fuzzy Sets and Soft Computing in Ecomomics and Finance, Saint-Petersburg, Russia, 17–20 June 2004; pp. 350–359. [Google Scholar]
- Charfeddine, S.; Zbidi, K.; Mora-Camino, F. Fuzzy Regression Analysis using Trapezoidal Fuzzy Numbers. In Proceedings of the EUSFLAT—LFA 2005, Barcelona, Spain, 7–9 September 2005; pp. 1213–1218. [Google Scholar]
- Ganesan, K.; Veeramani, P. Fuzzy Linear Programs with Trapezoidal Fuzzy Numbers. Ann. Oper. Res. 2006, 143, 305–315. [Google Scholar] [CrossRef]
- Kheirfam, B.; Verdegay, J.L. The dual simplex method and sensitivity analysis for fuzzy linear programming with symmetric trapezoidal numbers. Fuzzy Optim. Decis. Mak. 2013, 12, 171–189. [Google Scholar] [CrossRef]
- Kumar, A.; Kaur, J. A New Method for Solving Fuzzy Linear Programs with Trapezoidal Fuzzy Numbers. J. Fuzzy Set Valued Anal. 2011, 3, 103–118. [Google Scholar] [CrossRef]
- Fung, R.Y.K.; Chen, Y.; Tang, J. Estimating the functional relationships for quality function deployment under uncertainties. Fuzzy Sets Syst. 2006, 157, 98–120. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).