The Use of Stochastic Models for Short-Term Prediction of Water Parameters of the Thesaurus Dam, River Nestos, Greece ^†

Abstract

The scope of this paper is to evaluate the short-term predictive capacity of the stochastic models ARIMA, Transfer Function (TF) and Artificial Neural Networks for water parameters, specifically for 1, 2 and 3 steps forward (m = 1, 2 and 3). The comparison of statistical parameters indicated that ARIMA models could be proposed as short-term prediction models. In some cases that TF models resulted in better predictions, the difference with ARIMA was minimal and since the latter are simpler in their construction, they are proposed for short-term prediction. Artificial Neural Networks didn’t show a good short-term predictive capacity in comparison with the aforementioned models.

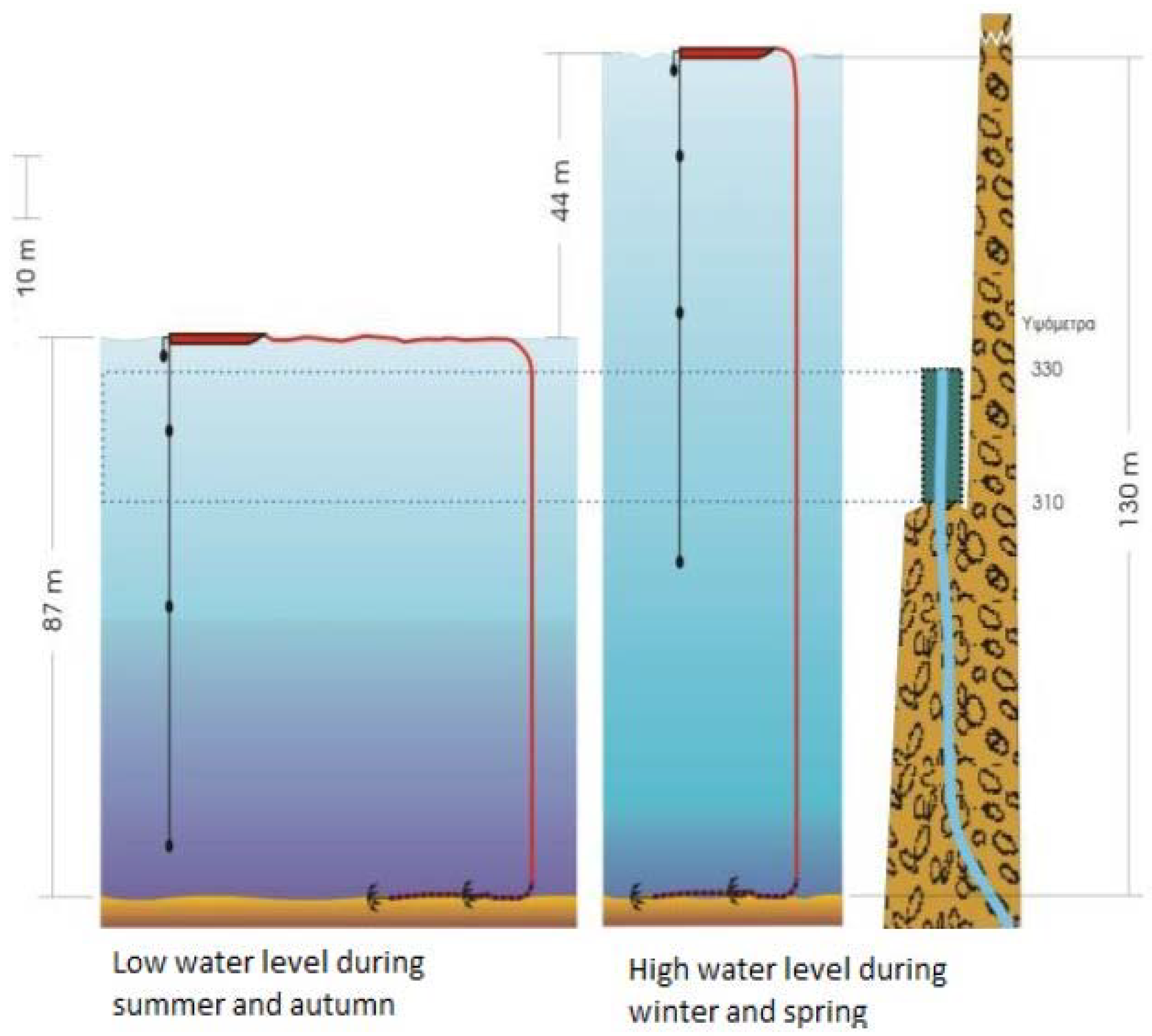
1. Introduction

The central part of River Nestos flow is one of the areas with the most intensive anthropogenic interference because of the construction and operation of Thesaurus and Platanovrissi dams. The purposes of the these dams are (a) hydroelectric power for the increased needs in the areas of Eastern Macedonia and Thrace; (b) anti-flooding protection of villages, cities, agricultural and touristic activities in Nestos downstream; (c) irrigation of the fertile deltaic plain and (d) ecological protection and preservation in Nestos Delta, which is one of the 11 Hellenic areas that is included in the Ramsar’s Convention [1,2].

In the deeper section of the reservoir basin, upstream of the Thesaurus dam, a floating telemetric station (Figure 1) was anchored to record changes in water temperature (Tw) and dissolved oxygen (DO) at four different depths (1, 20, 40 and 70 m). For these parameters, the daily records of the years 2004 to 2007 were analyzed and evaluated [3,4,5,6]. This research was completed by the end of the year 2007.

This study aims to evaluate the predictive capability of ARIMA, Transfer Function (TF) and Artificial Neural Networks (ANN) models for short-term prediction and more specifically for 1, 2 and 3 steps forward (m = 1, 2 and 3).

2. Methodology

An adequate number of continuous measurements (1440 on a daily basis) of the DO and Tw parameters, were used for the period from 19 January 2004 to 28 December 2007 and corresponded to four different depths (1, 20, 40 and 70 m). In order to evaluate the predictability of the models, the data set was split into two subsets: (a) the historical period with 1420 measurements and (b) the forecasting period with the last 20 measurements. The former was used to select the best adapted model in the data, while the latter was used in order to forecast the m step forward (${\widehat{y}}_t(m)$) [7,8,9].

If m = k then the prediction occurs for “k steps forward”; this means the prediction of the observation at time t + k, given the observations up to time t, which is called start time. Four statistical parameters, MSE, RMSE, MAPE and NSC, were used in order to assess the forecast. Finally, 95% confidence intervals were calculated for all the models selected [10].

The linear and nonlinear stochastic models which were tested are: (a) ARIMA, (b) Transfer Function and (c) Neural Network models. Their compilation, as well as the prediction results for m = 1, are discussed in detail in Sentas et al., 2016 [10].

The 20-day forecast was considered sufficient as the Thesaurus reservoir was first operated in 2000. Moreover, since the end of 1997, when its construction was completed, its water filling has begun. From the end of 1997 to the early 2000 some intense phenomena of water’s stationarity were observed, accompanied by anoxia, with reductive processes to dominate, by hydrogen sulfide production in the hypolimnion and by the development of sulfurbacteria [11].

By the time the reservoir started operating and the water being discharged for various uses (hydroelectric production, irrigation, flood protection, ecological), from the beginning of the year 2000 until nowadays, is still trying to restore the conditions of equilibrium between the natural environment and human interventions.

Thus, a period of four years (early 2004–late 2007) would be necessary for monitoring the hydro-system of Nestos-Thesaurus complex’s characteristics, throughout the water column and at various depths. This is because slight changes occur in those characteristics (e.g., the temperature in hypolimnion). In any other case of an existing reservoir, it would take a maximum of 2 years for complete monitoring and reliable results’ extraction. Nevertheless, in the case of the Thesaurus, it was considered that a database of 4 consecutive years is required.

Therefore, the forecasting was chosen to be performed at the end of the four-year period (December 2007), with no interim periods e.g., the spring of the same or the previous year, otherwise it would not exactly correspond to the interpretation of the physical problem.

3. Results

To test their predictive capacity, the following stochastic models were constructed and tested: (1) ARIMA, (2) Transfer Function and (3) Neural Network models. For each depth, an ARIMA model, a neural network model and a TF model were adapted to the dissolved oxygen time series. In total, four ARIMAs, four neural network models, and four TF models with a time-out of dissolved oxygen at each depth and input variable were adapted to the water depth of the corresponding depth. Using all of the above models, provision was made for m = 1 step forward [12,13,14,15].

ARIMA Models

For each depth, an ARIMA model, a neural network model and a TF model were adapted to the dissolved oxygen time series [12]. In total, four ARIMAs, four neural network models and four TF models with output variable the dissolved oxygen at each depth and input variable the temperature of the corresponding water depth, were adapted. By using all the aforementioned models, a short-term prediction was attempted for m = 1, 2 and 3 steps forward [16,17,18].

Details for the construction of the above models, as well as the prediction results for m = 1, are detailed in the paper Sentas et al., 2016 [10]. In the present paper, the results for 2 and 3 steps forward (m = 2 and 3) are reported. In parallel, the results for m = 1 are recorded in order to ensure better comprehension of short-term forecasting.

At 1m water depth the results are presented in

Table 1. Statistical parameters for comparison observed and predicted values using ARIMA, TF and ANN models and m = 1, 2 and 3 (depth 1 m).

Thesaurus Station—DO Parameter—Depth 1 m
${\widehat{\mathit{y}}}_{\mathit{t}}(\mathit{m})$	Μοdel	MSE	RMSE	MAPE	NSC
$m=1$	ARIMA	0.442	0.665	7.947	0.614
	TF	0.452	0.672	7.974	0.605
	ANN	0.523	0.723	8.934	0.544
$m=2$	ARIMA	0.852	0.923	11.158	0.256
	TF	0.816	0.903	10.589	0.196
	ANN	1.010	1.005	12.002	0.599
$m=3$	ARIMA	0.960	0.979	11.713	0.163
	TF	0.938	0.968	11.562	0.532
	ANN	1.182	1.087	12.182	0.545

. ${\widehat{y}}_t(m)$, represents the forecast at the time $t+m$ of a time series, in which observations are known up to time t. Similarly the results for depths 20, 40 and 70 meters are given in

Table 2. Statistical parameters for comparison of observed and predicted values using ARIMA, TF and ANN models and m = 1, 2 and 3 (20 m depth).

Thesaurus Station—DO Parameter—Depth 20 m
${\widehat{\mathit{y}}}_{\mathit{t}}(\mathit{m})$	Model	MSE	RMSE	MAPE	NSC
$m=1$	ARIMA	0.0077	0.0877	1.0552	0.7992
	TF	0.0079	0.0891	1.0752	0.7931
	ANN	0.0434	0.2084	2.6721	−0.1303
$m=2$	ARIMA	0.0154	0.1241	1.505	0.9913
	TF	0.0163	0.1278	1.6945	0.5751
	ANN	0.0570	0.2387	3.0021	0.0191
$m=3$	ARIMA	0.0215	0.1466	1.9787	0.9881
	TF	0.0228	0.1511	2.0194	0.4061
	ANN	0.0882	0.2969	3.2124	0.0072

,

Table 3. Statistical parameters for comparison of observed and predicted values using ARIMA, TF and ANN models and m = 1, 2 and 3 (40 m depth).

Thesaurus Station—DO Parameter—Depth 40 m
${\widehat{\mathit{y}}}_{\mathit{t}}(\mathit{m})$	Μοdel	MSE	RMSE	MAPE	NSC
$m=1$	ARIMA	0.0167	0.1293	1.5882	0.9167
	TF	0.0131	0.1144	1.4791	0.9341
	ANN	0.0170	0.1305	1.6781	0.9154
$m=2$	ARIMA	0.0545	0.2334	2.5415	0.9245
	TF	0.0301	0.1732	2.0954	0.7155
	ANN	0.0510	0.2258	2.7102	0.6112
$m=3$	ARIMA	0.0741	0.2722	3.6787	0.9611
	TF	0.0515	0.2269	3.0231	0.5930
	ANN	0.0893	0.2988	3.7487	0.4327

and

Table 4. Statistical parameters for comparison of observed and predicted values using ARIMA, TF and ANN models and m = 1, 2 and 3 (70 m depth).

Thesaurus Station—DO Parameter—Depth 70 m
${\widehat{\mathit{y}}}_{\mathit{t}}(\mathit{m})$	Μοdel	MSE	RMSE	MAPE	NSC
$m=1$	ARIMA	0.1376	0.3709	4.4140	−0.170
	TF	0.1413	0.3759	4.3697	−0.202
	ANN	0.1913	0.4375	5.860	−0.628
$m=2$	ARIMA	0.1470	0.3834	5.1874	−0.1809
	TF	0.1725	0.4153	5.4653	0.0325
	ANN	0.2130	0.4615	5.9012	−0.1109
$m=3$	ARIMA	0.1760	0.4195	6.2807	−0.1771
	TF	0.2010	0.4484	6.7227	0.0298
	ANN	0.2278	0.4772	7.0136	−0.0208

, respectively.

The values listed in Table 1 lead to the conclusion that for both $m=2$ and $m=3$, the TF model shows slightly better values for the statistical parameters than ARIMA and better than ANN, except in the case of the parameter NSC according to which the ANN model precedes.

At water depth of 20 m, according to Table 2, for m = 1, 2 and 3, the ARIMA model results in better predictions with slight differences from the TF models.

At 40 m water depth, according to Table 3, in all cases (m = 1, 2 and 3) the TF models show better statistics. Also, the difference in the statistical parameters for steps 1, 2 and 3 between ARIMA and TF models is small.

At 70 m water depth, according to Table 4, for prediction of 1, 2 and 3 steps forward (m = 1, 2 and 3) the ARIMA models seem to precede in comparison to the others.

3. Conclusions

This paper is focused on the comparative evaluation of the short-term predictive capacity of the stochastic models ARIMA, Transfer Function (TF) and Artificial Neural Networks. An adequate sample of four years daily monitoring program (19 January 2004–28 December 2007), of approximately 1440 records of Dissolved Oxygen (DO) and Water Temperature (Tw) parameters in Lake Thesaurus, were used in Monitoring Stations in four different depths (1, 20, 40 and 70 m).

In order to evaluate the predictability of the models, the data set was split into two subsets: (a) the historical period with 1420 measurements and (b) the forecasting period with the last 20 measurements. The former was used to select the best adapted model in the data, while the latter was used in order to forecast the m step forward (${\widehat{y}}_t(m)$) [7,8,9].

For the short-term prediction of m = 1, 2 and 3 steps forward, the performance of ARIMA models and—in some cases—TF models, is better with slight difference. This is due to the fact that as the distance between the starting point and the forecast increases (m increases), the contribution of the parameter observed values to the estimation of the forecast is diminished. ARIMA models could be proposed as short-term prediction models, although in some cases TF models resulted in better predictions, because (a) the difference with ARIMA models was not statistically significant and (b) the latter are simpler in their construction. On the other hand, Artificial Neural Networks didn’t show a good short-term predictive capacity in comparison with the aforementioned models.

In order to predict more precisely the ${\widehat{y}}_t(m)$ values, the estimated values of $y_t$are used and not the observed ones. Therefore, the contribution of the observed values of water temperature at the corresponding depths, becomes more significant to the estimation of the forecasting values and the TF models result in better predictions than ARIMA.

To summarize, short-term forecasts of up to four days could be performed by both ARIMA and TF models. Nevertheless, ARIMA models are proposed due to their simplicity both regarding their compilation and use [6,7,17,18].

Further research can take place in three aspects: (a) applying forecasting for long—term prediction (m = 10, 15,…); (b) comparing these models with other forecasting models and (c) applying these models in other deep water bodies and assess the comparison between them. The statistical analysis and stochastic modelling are very helpful tools to the assessment of water quality and quantity issues and could set the fountains for the Integrated Management of both aquatic ecosystems and water resources.