Wave-Current Interactions and Infragravity Wave Propagation at a Microtidal Inlet †
Abstract
:1. Introduction
2. Methods and Results
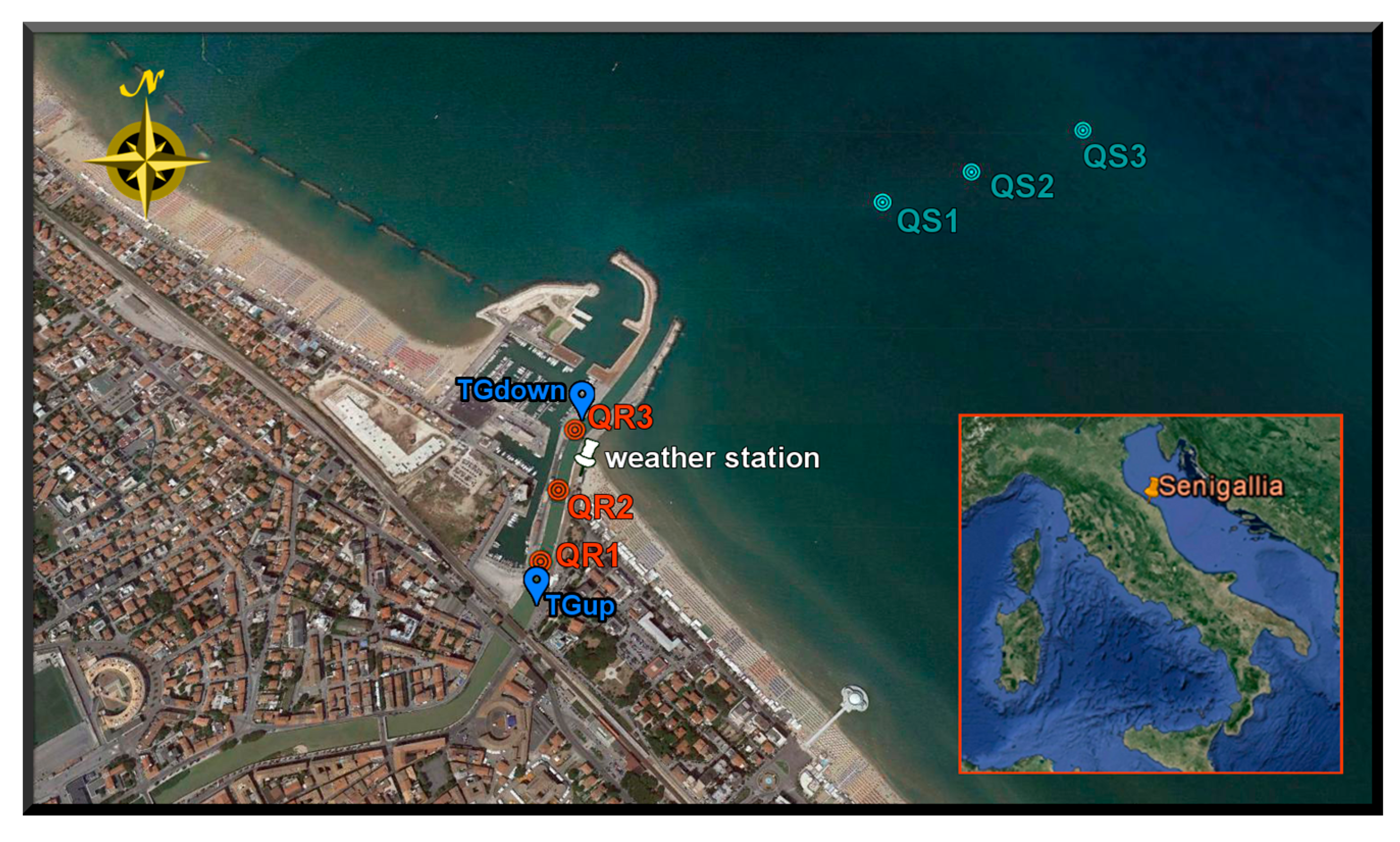
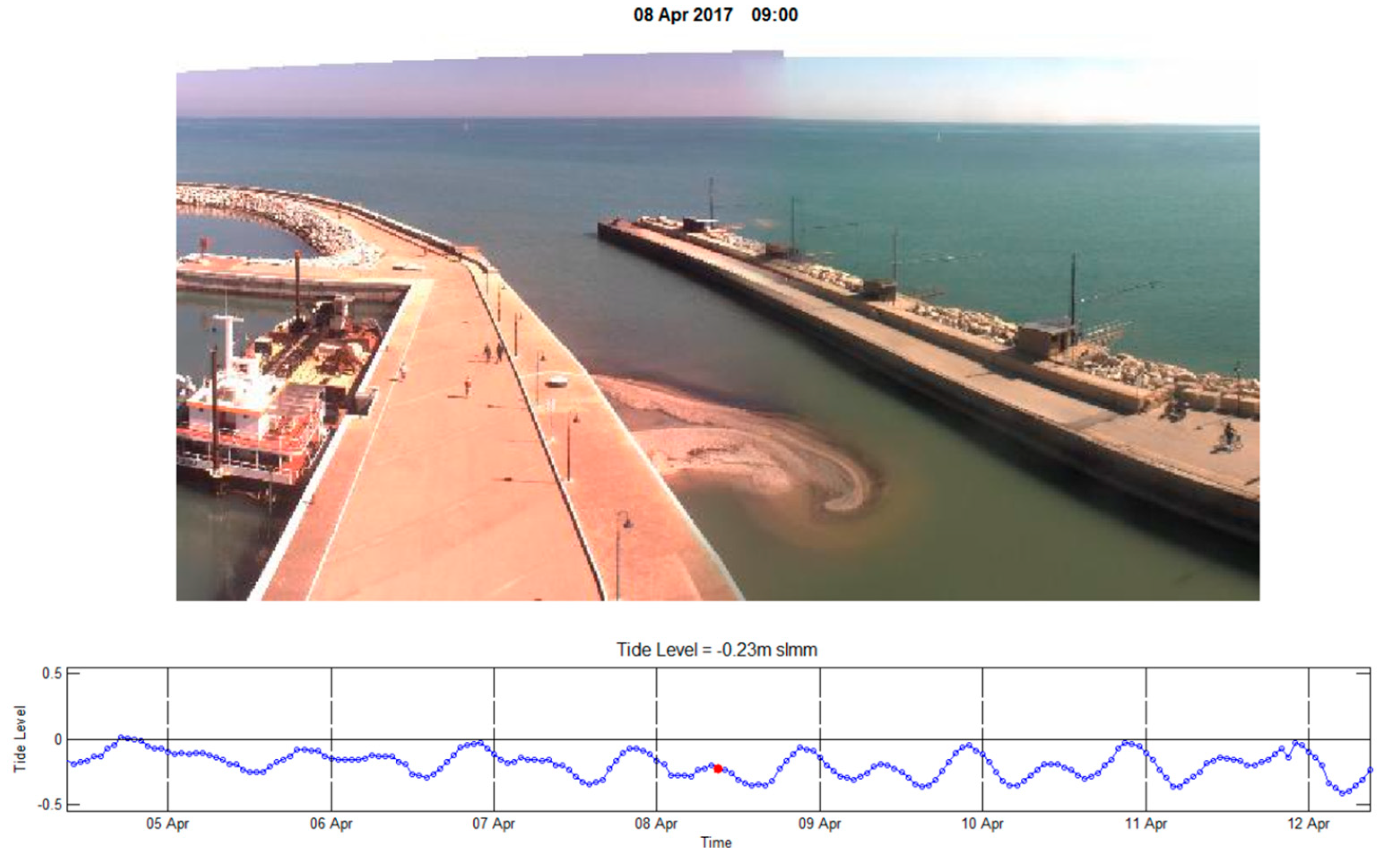
2.1. The EsCoSed Field Campaign
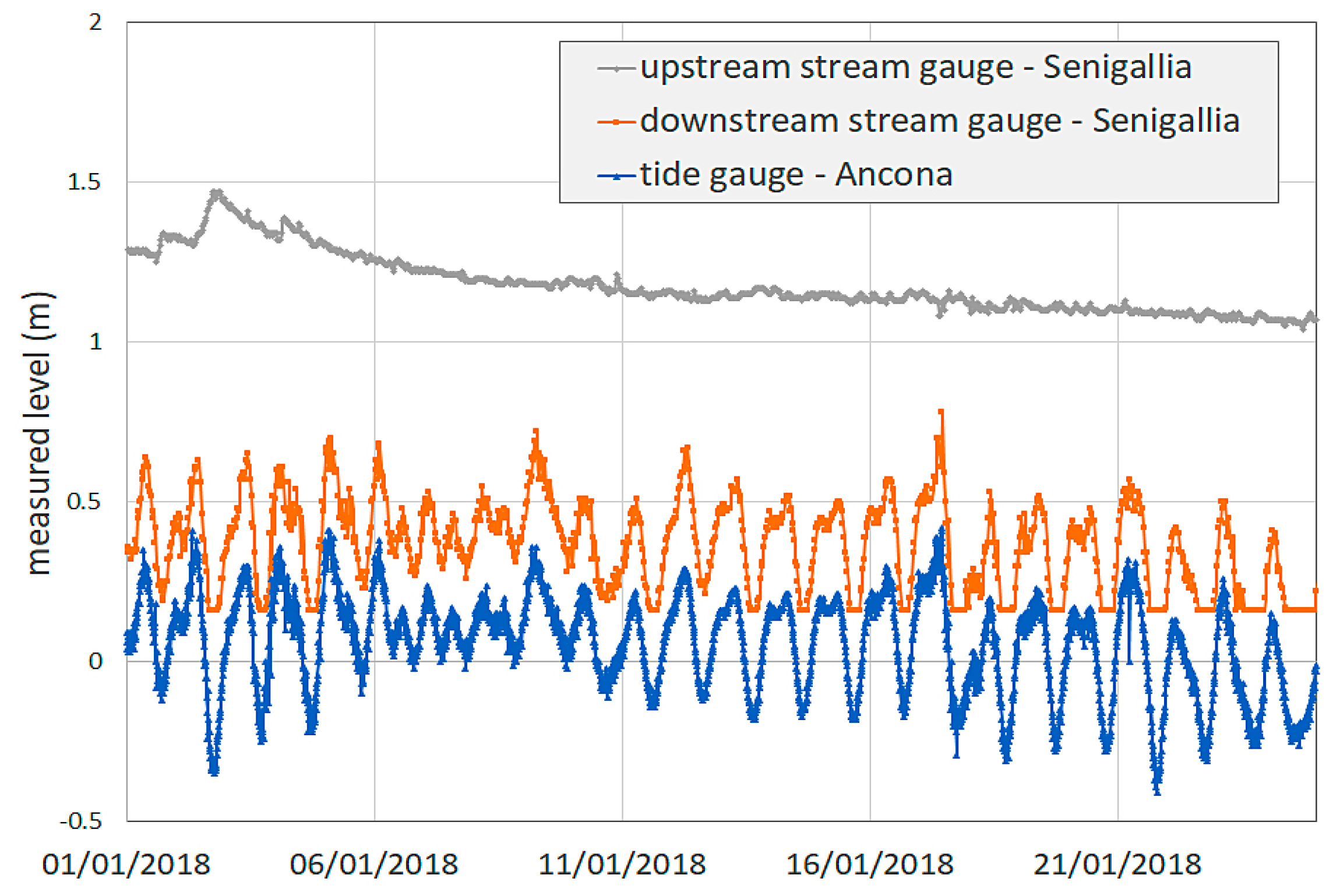
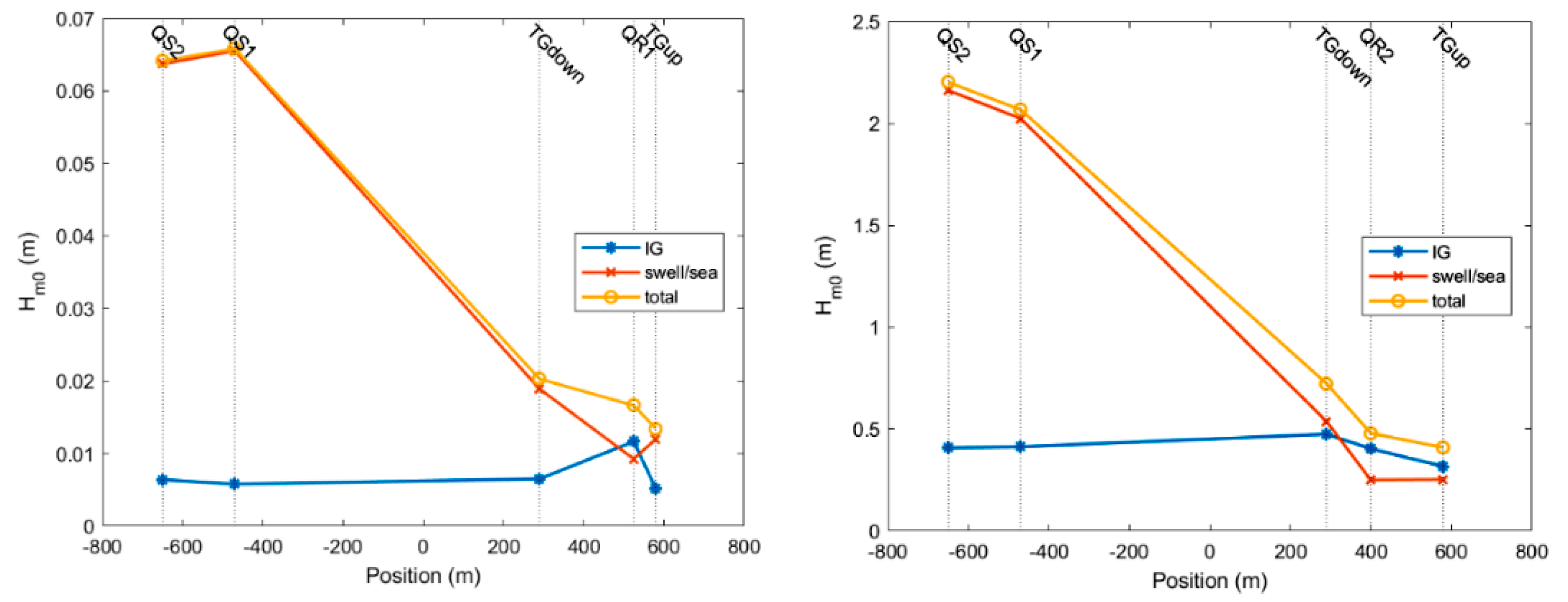
2.2. Experimental Evidence of IG Waves at the MR
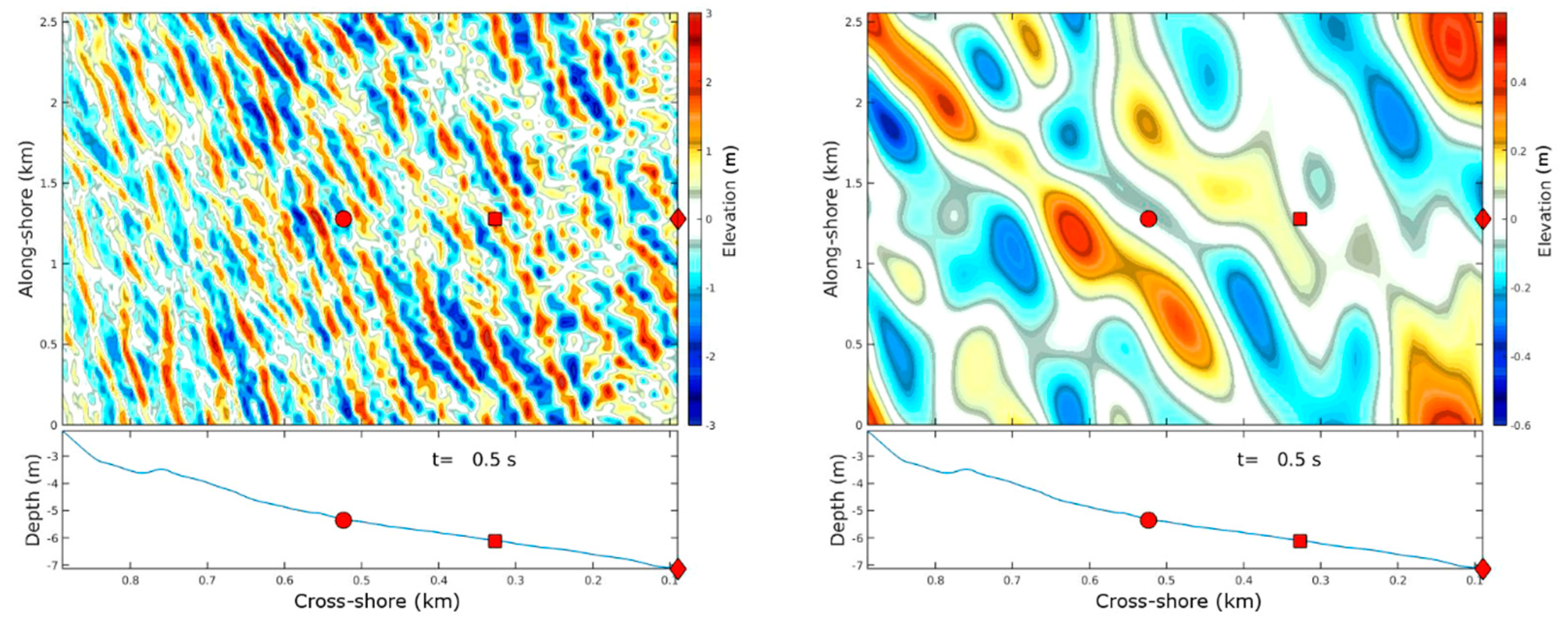
2.3. TRIADS Sample Computation of the Generation of IG from the Local Wave Field
3. Discussion and Conclusions
Acknowledgments
References
- Chawla, A.; Kirby, J.T. Monochromatic and random wave breaking at blocking points. J. Geophys. Res. Oceans 2002, 107, 4-1–4-19. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Edmonds, D.A.; Nardin, W.; Leonardi, N.; Canestrelli, A.; Falcini, F.; Jerolmack, D.J.; Mariotti, G.; Rowland, J.C.; Slingerland, R.L. Dynamics of river mouth deposits. Rev. Geophys. 2015, 53, 642–672. [Google Scholar] [CrossRef]
- Nardin, W.; Mariotti, G.; Edmonds, D.A.; Guercio, R.; Fagherazzi, S. Growth of river mouth bars in sheltered bays in the presence of frontal waves. J. Geophys. Res. Earth Surf. 2013, 118, 872–886. [Google Scholar] [CrossRef]
- Jerolmack, D.J.; Swenson, J.B. Scaling relationships and evolution of distributary networks on wave-influenced deltas. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Davidson-Arnott, R. An Introduction to Coastal Processes and Geomorphology; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Munk, W.H. Origin and generation of waves. In Proceedings of the First Conference on Coastal Engineering, Long Beach, CA, USA, October 1950. [Google Scholar]
- Aucan, J.; Ardhuin, F. Infragravity waves in the deep ocean: An upward revision. Geophys. Res. Lett. 2013, 40, 3435–3439. [Google Scholar] [CrossRef]
- Aagaard, T.; Hughes, M. Sediment transport. In Reference Module in Earth Systems and Environmental Sciences; Elsevier Science: New York, NY, USA, 2013; pp. 74–105. [Google Scholar]
- Uncles, R.J.; Stephens, J.A.; Harris, C. Infragravity currents in a small ría: Estuary-amplified coastal edge waves? Estuar. Coast. Shelf Sci. 2014, 150, 242–251. [Google Scholar] [CrossRef]
- Bertin, X.; Olabarrieta, M. Relevance of infragravity waves in a wave-dominated inlet. J. Geophys. Res. Oceans 2016, 121, 5418–5435. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stresses in water waves; a physical discussion, with applications. Deep Sea Res. Oceanogr. Abstr. 1964, 11, 529–562. [Google Scholar] [CrossRef]
- Symonds, G.; Huntley, D.A.; Bowen, A.J. Two-dimensional surf beat: Long wave generation by a time-varying breakpoint. J. Geophys. Res. Oceans 1982, 87, 492–498. [Google Scholar] [CrossRef]
- Brocchini, M.; Calantoni, J.; Postacchini, M.; Sheremet, A.; Staples, T.; Smith, J.; Reed, A.H.; Braithwaite, E.F., III; Lorenzoni, C.; Russo, A.; et al. Comparison between the wintertime and summertime dynamics of the Misa River estuary. Mar. Geol. 2017, 385, 27–40. [Google Scholar] [CrossRef]
- Brocchini, M.; Calantoni, J.; Reed, A.H.; Postacchini, M.; Lorenzoni, C.; Russo, A.; Mancinelli, A.; Corvaro, S.; Moriconi, G.; Soldini, L. Summertime conditions of a muddy estuarine environment: The EsCoSed project contribution. Water Sci. Technol. 2015, 71, 1451–1457. [Google Scholar] [CrossRef] [PubMed]
- Wright, L.D.; Short, A.D. Morphodynamic variability of surf zones and beaches: A synthesis. Mar. Geol. 1984, 56, 93–118. [Google Scholar] [CrossRef]
- Masselink, G.; Short, A.D. The effect of tide range on beach morphodynamics and morphology: A conceptual beach model. J. Coast. Res. 1993, 9, 785–800. [Google Scholar]
- Freilich, M.H.; Guza, R.T. Nonlinear effects of shoaling surface gravity waves. Philos. Trans. R. Soc. Lond. A 1983, 311, 1–41. [Google Scholar]
- Agnon, Y.; Sheremet, A.; Gonsalves, J.; Stiassnie, M. A unidirectional model for shoaling gravity waves. Coast. Eng. 1993, 20, 29–58. [Google Scholar] [CrossRef]
- Davis, J.R.; Sheremet, A.; Tian, M.; Saxena, S. A numerical implementation of a nonlinear mild slope model for shoaling directional waves. J. Mar. Sci. Eng. 2014, 2, 140–158. [Google Scholar] [CrossRef]
- Sheremet, A.; Davis, J.R.; Tian, M.; Hanson, J.L.; Hathaway, K.K. TRIADS: A phase resolving model for nonlinear shoaling of directional waves. Ocean Model. 2016, 99, 60–74. [Google Scholar] [CrossRef]
- Perugini, E.; Soldini, L.; Palmsten, M.L.; Calantoni, J.; Brocchini, M. A new video monitoring station along the Adriatic coast. In Proceedings of the Convegno Nazionale di Idraulica e Costruzioni Idrauliche, Ancona, Italy, 12–14 September 2018. [Google Scholar]

| Season | tanβ | Depth (m) | Hb (m) | T (s) | Ws (m/s) | MSTR (m) |
|---|---|---|---|---|---|---|
| Winter | 0.01 | 7 | 3 | 9.5 | 0.011–0.032 | 0.5 |
| Summer | 0.01 | 7 | 1 | 6 | 0.011–0.032 | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melito, L.; Postacchini, M.; Sheremet, A.; Calantoni, J.; Zitti, G.; Darvini, G.; Brocchini, M. Wave-Current Interactions and Infragravity Wave Propagation at a Microtidal Inlet. Proceedings 2018, 2, 628. https://doi.org/10.3390/proceedings2110628
Melito L, Postacchini M, Sheremet A, Calantoni J, Zitti G, Darvini G, Brocchini M. Wave-Current Interactions and Infragravity Wave Propagation at a Microtidal Inlet. Proceedings. 2018; 2(11):628. https://doi.org/10.3390/proceedings2110628
Chicago/Turabian StyleMelito, Lorenzo, Matteo Postacchini, Alex Sheremet, Joseph Calantoni, Gianluca Zitti, Giovanna Darvini, and Maurizio Brocchini. 2018. "Wave-Current Interactions and Infragravity Wave Propagation at a Microtidal Inlet" Proceedings 2, no. 11: 628. https://doi.org/10.3390/proceedings2110628
APA StyleMelito, L., Postacchini, M., Sheremet, A., Calantoni, J., Zitti, G., Darvini, G., & Brocchini, M. (2018). Wave-Current Interactions and Infragravity Wave Propagation at a Microtidal Inlet. Proceedings, 2(11), 628. https://doi.org/10.3390/proceedings2110628







