Parameter Optimization of a Bed Load Transport Formula for Nestos River, Greece ^†

Abstract

In the Second EWaS International Conference (June 2016, Chania, Crete, Greece), the bed load transport formula of Meyer-Peter and Müller (1948) was calibrated with respect to the bed roughness coefficient for Nestos River. The calibration was manual and incremental, taking five measured values of bed load transport rate at a time. In contrast, the present study carries out a nonlinear optimization of two suitable parameters, while utilizing the average value of the roughness coefficient k_st found by the manual calibration. Thus, a uniform calibration is attained, by taking at once the totality of the available 68 measurement points. The results did not show any marked fitting improvement in comparison to the previous study. However, considering moving averages of the measured bed load transport values yields a better adjustment of the model to the measured results.

1. Introduction

No systematic river bed load transport measurements have been conducted and published in Greece to date. An effort to carry out such measurements has been undertaken through diploma projects, by the Division of Hydraulic Engineering, Civil Engineering Department of the Democritus University of Thrace [1,2,3]. The measurements were taken at mountainous outlets of the river basins leading to Kosynthos River and Kimmeria Torrent. Those outlets are located in the area of the city of Xanthi, the seat of the Democritus University Engineering Faculty. Due to the well-known stream flow rate dependence of both bed load and suspended load transport rates, measurements of the first quantity preceded those of the other two.

In the framework of those studies, nonlinear regression equations were presented (a) between bed load transport rate and stream flow rate based on 24 measurements and (b) suspended load transport rate and stream flow rate based on 29 measurements, of both variables in each case [2].

In this paper, 68 pairs of stream flow rate and bed load transport rate measurements of Nestos River are presented. Beside those measurements, the bed load transport rate was calculated by the Meyer-Peter and Müller formula (1948), thus enabling comparisons between measured and computed results.

The above formula was applied in recent years to bed load computations in streams and rivers in various parts of the world, notably in France [4] and Spain [5,6]. This paper represents an attempt for an overall calibration of the Meyer-Peter and Müller formula that covers multiple sets of measurements, in contrast to partial calibrations referred to individual measurement sets.

2. Study Area

The study area is described in [7], and this description is repeated here for reasons of completeness.

The Nestos River basin considered in this study drains an area of 838 km² and lies downstream of Platanovrysi Dam. The river basin outlet is located at Toxotes. The river basin terrain is covered by forest (48%), bush (20%), cultivated land (24%), urban area (2%) and no significant vegetation (6%). The altitude ranges between 80 m and 1600 m, whereas the length of Nestos River is 55 km. The basin is divided into 20 natural sub-basins with areas between 13 km² and 80 km². The mean slope of the sub-basins ranges between 23% and 58%, the mean slope of the main streams of the sub-basins ranges between 2.5% and 20%, whereas the mean slope of Nestos River in the basin is 0.35%.

3. Stream Flow Rate and Bed Load Transport Rate Measurements

The stream flow rate and bed load transport rate measurements concerning Nestos River were conducted at a location between the outlet of Nestos River basin (Toxotes) and the river delta (e.g., [8,9,10,11,12]). The measurement procedures are described in [7]. The average width of the cross sections of all measurements is about 26.7 m. The dates of all measurements as well as the stream flow rates and bed load transport rates of Nestos River are presented in

Table A1. Stream flow rate and bed load transport rate measurements of Nestos River—Calculated bed load transport rate.

No of Measurement	Date	Stream Flow Rate (m3/s)	Bed Load Transport Rate	Bed Load Transport Rate	Bed Load Transport Rate
			(kg/(m·s))	(kg/(m·s))	(kg/(m·s))
			Site-Measured	Calculated (Manual Calibration)	Calculated (Parameters)
1	26 September 2005	14.170	0.0240	0.0193	0.0537
2	27 September 2005	17.440	0.0300	0.0232	0.0579
3	29 September 2005	16.650	0.0440	0.0323	0.0585
4	30 September 2005	18.490	0.0270	0.0313	0.0571
5	30 October 2008	2.729	0.0033	0.0031	0.0479
6	1 November 2008	2.694	0.0025	0.0017	0.0485
7	3 November 2008	3.086	0.0033	0.0044	0.0520
8	21 July 2010	3.954	0.0433	0.0501	0.0702
9	22 July 2010	4.223	0.0499	0.0408	0.0690
10	22 July 2010	4.129	0.0594	0.0339	0.0682
11	26 July 2010	6.198	0.0425	0.0671	0.0680
12	27 July 2010	4.798	0.0599	0.0629	0.0688
13	29 July 2010	3.763	0.0638	0.0391	0.0682
14	3 August 2010	3.161	0.0349	0.0276	0.0709
15	5 August 2010	9.951	0.0143	0.0275	0.0513
16	15 September 2010	4.217	0.0226	0.0210	0.0509
17	30 September 2010	4.802	0.0283	0.0253	0.0503
18	2 November 2010	2.055	0.0515	0.0393	0.0484
19	3 November 2010	1.882	0.0499	0.0465	0.0462
20	5 November 2010	1.489	0.0594	0.0422	0.0503
21	5 November 2010	1.747	0.0425	0.0404	0.0535
22	18 November 2010	1.661	0.0068	0.0083	0.0546
23	25 November 2010	1.546	0.0173	0.0179	0.0537
24	26 November 2010	1.651	0.0160	0.0096	0.0499
25	3 December 2010	2.029	0.0038	0.0047	0.0472
26	3 December 2010	0.800	0.0046	0.0062	0.0486
27	24 March 2011	3.269	0.0189	0.0185	0.0552
28	25 March 2011	2.234	0.0465	0.0454	0.0480
29	29 March 2011	2.831	0.0151	0.0253	0.0547
30	2 April 2011	3.399	0.0304	0.0274	0.0547
31	2 April 2011	3.285	0.0177	0.0349	0.0492
32	7 April 2011	1.772	0.0202	0.0307	0.0528
33	9 April 2011	1.055	0.0101	0.0180	0.0523
34	27 April 2011	3.676	0.0152	0.0301	0.0543
35	20 November 2011	1.813	0.0292	0.0316	0.0510
36	22 November 2011	0.586	0.0175	0.0088	0.0564
37	14 March 2012	1.061	0.0246	0.0291	0.0510
38	15 March 2012	1.428	0.0389	0.0750	0.0488
39	16 September 2012	0.507	0.0020	0.0035	0.0495
40	23 September 2012	0.882	0.0062	0.0066	0.0487
41	11 November 2012	1.360	0.0143	0.0107	0.0457
42	26 November 2012	0.796	0.0128	0.0199	0.0541
43	26 November 2012	0.837	0.0183	0.0224	0.0530
44	26 November 2012	0.927	0.0120	0.0099	0.0523
45	27 November 2012	1.593	0.0816	0.0421	0.0464
46	27 November 2012	0.875	0.0038	0.0023	0.0595
47	27 November 2012	2.048	0.0468	0.0399	0.0532
48	28 November 2012	1.059	0.0062	0.0087	0.0514
49	28 November 2012	0.851	0.0115	0.0058	0.0462
50	16 July 2013	0.493	0.0339	0.0535	0.0525
51	14 May 2014	5.450	0.0193	0.0174	0.0500
52	14 May 2014	6.605	0.0102	0.0134	0.0508
53	15 June 2014	9.750	0.0204	0.0342	0.0480
54	15 June 2014	12.980	0.0139	0.0185	0.0503
55	16 June 2014	9.833	0.0385	0.0313	0.0558
56	18 October 2014	6.538	0.2127	0.2020	0.0697
57	18 October 2014	4.317	0.2692	0.1808	0.0527
58	18 October 2014	6.110	0.2022	0.2105	0.0551
59	19 October 2014	9.660	0.5370	0.3523	0.0452
60	19 October 2014	2.256	0.1087	0.0656	0.0573
61	19 October 2014	2.225	0.0625	0.0718	0.0525
62	19 October 2014	5.743	0.1511	0.2086	0.0527
63	19 October 2014	2.379	0.0421	0.0805	0.0524
64	19 October 2014	6.153	0.2120	0.2000	0.0509
65	20 October 2014	2.930	0.0616	0.0851	0.0422
66	20 October 2014	6.930	0.2920	0.2222	0.0549
67	20 October 2014	9.760	0.6173	0.6173	0.0441
68	21 October 2014	13.410	0.6030	0.4366	0.0550

, which is given in the Appendix A.

4. Bed Load Transport Rate Calculations

The following well-known formula of Meyer-Peter and Müller (1948) [13] was employed:

$${\mathrm{m}}_{\mathrm{G}}=\frac{8}{\mathrm{g}}\frac{{\mathsf{\rho }}_{\mathrm{F}}}{{\mathsf{\rho }}_{\mathrm{F}}-{\mathsf{\rho }}_{\mathrm{W}}}\sqrt{\frac{1}{{\mathsf{\rho }}_{\mathrm{W}}}}{\left({\mathsf{\tau }}_{\mathsf{o}}-{\mathsf{\tau }}_{\mathsf{o},\mathrm{cr}}\right)}^{3/2}$$

(1)

where

$${\mathsf{\tau }}_{\mathsf{o}}={\mathsf{\rho }}_{\mathrm{W}}{\mathrm{gI}}_{\mathrm{r}}{\mathrm{R}}_{\mathrm{s}}$$

(2)

$${\mathsf{\tau }}_{\mathsf{o},\mathrm{cr}}=0.047{{\mathsf{\rho }}^{\prime }\mathsf{\rho }}_{\mathrm{W}}{\mathrm{gd}}_{\mathrm{m}}$$

(3)

$${\mathsf{\rho }}^{\prime }=\frac{{\mathsf{\rho }}_{\mathrm{F}-}{\mathsf{\rho }}_{\mathrm{W}}}{{\mathsf{\rho }}_{\mathrm{W}}}$$

(4)

$${\mathrm{I}}_{\mathrm{r}}={(\frac{{\mathrm{k}}_{\mathrm{st}}}{{\mathrm{k}}_{\mathrm{r}}})}^{3/2}\mathrm{I}$$

(5)

$${\mathrm{k}}_{\mathrm{r}}=\frac{26}{\sqrt[6]{{\mathrm{d}}_{90}}}$$

(6)

m_G: bed load transport rate per unit width (kg/(m·s))

g: gravity acceleration (m/s²)

ρ_F: sediment density (kg/m³)

ρ_W: water density (kg/m³)

τ_ο: actual shear stress (N/m²)

τ_ο,cr: critical shear stress (N/m²)

d_m: bed load particles mean diameter (m)

I_r: energy line slope due to individual particles

R_s: hydraulic radius of the specific part of the cross section under consideration which affects the bed load transport (m)

I: energy line slope due to individual particles and stream bed forms

k_r: coefficient, the value of which depends on the roughness due to individual particles (m^1/3/s)

k_st: Strickler coefficient, the value of which depends on the roughness due to individual particles as well as to stream bed forms (m^1/3/s)

d₉₀: characteristic grain size diameter (m) (in case of taking a sample of stream bed load, the 90% of the sample weight is comprised by grains with size less or equal to d₉₀).

From Equation (1) is evident that bed load transport rate is expressed as a function of the difference between the actual shear stress and the critical shear stress, which is associated with the initiation of movement of the stream bed particles.

As pointed out in [3], the mechanisms involved in the Meyer-Peter and Müller model [13] and the Einstein- Barbarossa method [14] lead to the formula of Equation (7) for the stream cross section A:

$$\mathrm{A}={\mathrm{A}}_{\mathrm{s}}+{\mathrm{A}}_{\mathrm{w}}={\mathrm{R}}_{\mathrm{s}}{\mathrm{U}}_{\mathrm{s}}+{\mathrm{R}}_{\mathrm{w}}{\mathrm{U}}_{\mathrm{w}}$$

(7)

where R is the hydraulic radius and U the wetted perimeter. The index s refers to the bed and the index w to the walls. The hydraulic radii Rw and Rs are given by Equations (8) and (9), as derived in [3]:

$${\mathrm{R}}_{\mathrm{w}}={(\frac{{\mathrm{u}}_{\mathrm{m}}}{{\mathrm{k}}_{\mathrm{w}}{\mathrm{I}}^{0.5}})}^{1.5}$$

(8)

$${\mathrm{R}}_{\mathrm{s}}=\frac{\mathrm{A}-{\left(\frac{{\mathrm{u}}_{\mathrm{m}}}{{\mathrm{k}}_{\mathrm{w}}{\mathrm{I}}^{0.5}}\right)}^{1.5}{\mathrm{U}}_{\mathrm{w}}}{{\mathrm{U}}_{\mathrm{s}}}$$

(9)

where u_m (m/s) is the mean flow velocity through the cross-sectional area A and k_w (m^1/3/s) a coefficient depending on the roughness of the walls. Also k_w = k_st, and I is set equal to the longitudinal stream bed slope on the basis of the assumption of uniform flow. As in [3], an equivalent rectangular cross section is considered, and the median particle diameter d₅₀ substitutes the mean particle diameter d_m, because grain size distribution curves are available for all the bed load transport rate measurements. The median particle diameter is considered as representative of the different particle diameters of the bed load material.

5. Manual Calibration of the Meyer-Peter and Müller Formula

In the framework of the elaborated diploma theses, the estimation of the Strickler coefficient k_st, which refers to the total roughness, due to individual particles as well as to stream bed forms, was performed employing a manual calibration procedure, namely assuming that the bed load transport rate m_G is well-known from the measurements. In concrete terms, the measurements conducted by the same students group, were used for the determination of the coefficient k_st. If, for example, five measurements, as usually, were conducted by a students group, then five values of k_st were determined, and finally, the mean value of the five k_st values was taken into account for the calculation of the five bed load transport rates. The mean value of k_st for Nestos River, according to the above described manual calibration, amounts to about 18.5 m^1/3/s.

The outcomes of the calculations of bed load transport rate for Nestos River are given in Table A1.

6. Calibration of the Bed Load Transport Model for Nestos River

According to the model employed (Equations (1)–(6)), the computed value of the bed load transport rate, denoted as m_Gci, is equal to:

$${\mathrm{m}}_{\mathrm{Gci}}=\frac{8}{\mathrm{g}}\frac{{\mathsf{\rho }}_F}{{\mathsf{\rho }}_{\mathrm{F}}-{\mathsf{\rho }}_{\mathrm{W}}}\sqrt{\frac{1}{{\mathsf{\rho }}_{\mathrm{W}}}}{\left({\mathsf{\tau }}_{\mathrm{oi}}-{\mathsf{\tau }}_{\mathrm{o},\mathrm{cri}}\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

(10)

where

$${\mathsf{\tau }}_{oi}={\mathsf{\rho }}_{\mathrm{W}}\mathrm{g}{\left(\frac{{\mathrm{k}}_{\mathrm{st}}}{{\mathrm{k}}_{\mathrm{ri}}}\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\mathrm{IR}}_{\mathrm{si}}$$

(11)

$${\mathrm{R}}_{\mathrm{si}}=\left[{\mathrm{A}}_{\mathrm{i}}-{\left(\frac{{\mathrm{u}}_{\mathrm{mi}}}{{\mathrm{k}}_{\mathrm{st}}{\mathrm{I}}^{0.5}}\right)}^{1.5}{\mathrm{U}}_{\mathrm{wi}}\right]\frac{1}{{\mathrm{U}}_{\mathrm{si}}}$$

(12)

and

$${\mathsf{\tau }}_{\mathrm{o},\mathrm{cr}i}=0.047{{\mathsf{\rho }}^{\prime }\mathsf{\rho }}_{\mathrm{W}}{\mathrm{gd}}_{\mathrm{mi}}$$

(13)

In the present work, k_st is treated as a parameter of adjustment to be determined through the minimization of the sum of squares of the differences between computed and measured values of sediment transport rate:

$$\mathrm{f}\left({\mathrm{k}}_{\mathrm{st}}\right)={\displaystyle \sum }_{\mathrm{i}}{\left({\mathrm{m}}_{{\mathrm{G}}_{\mathrm{ci}}}-{\mathrm{m}}_{{\mathrm{G}}_{\mathrm{mi}}}\right)}^2$$

(14)

An improved fit is achieved if the objective function of Equation (14) is equipped with two further parameters α and β, as follows:

$$\mathrm{f}\left({\mathrm{k}}_{\mathrm{st}};\mathsf{\alpha },\mathsf{\beta }\right)={\displaystyle \sum }_{\mathrm{i}}{\left({\mathsf{\alpha }\mathrm{m}}_{{\mathrm{G}}_{\mathrm{ci}}}\left(\mathsf{\beta }\right)-{\mathrm{m}}_{{\mathrm{G}}_{\mathrm{mi}}}\right)}^2$$

(15)

In Equation (15) above, α is a scaling parameter and β replaces the exponent (3/2) in Equations (10) and (11). Both parameters are strictly positive. Thus, Equation (15) expresses the objective function of the problem, which is posed as follows: Minimize f with respect to α and β for a range of values of the physical parameter k_st.

The consideration of both parameters α and β simultaneously is the point at which the present study differs from the one presented in [3].

The value of k_st, k_st = 18.447 m^1/3/s, was derived through manual calibration of the Meyer-Peter and Müller model [13] on the basis of the 68 measurements, as described in [7].

The corresponding optimal values of α and β are: α = 0.427401, β = 0.209616.

Figure 1 shows measured (m_Gmi) versus calibrated computed (m_Gci) values.

If instead of the measured bed load values themshelves, their 5-point moving average is considered, then these moving averages present a better agreement to the respective values computed on the basis of the same model. The value of k_st was again taken equal to k_st = 18.447 m^1/3/s, but the optimal values of the parameters α and β are in this case α = 0.000325756, β = 2.15642.

Figure 2 shows 5-point moving average measured (m_Gmi) versus calibrated computed (m_Gci) values.

The adjustment of the model to the moving averages, as shown in Figure 2, is obviously better in comparison to the one depicted in Figure 1.

7. Comparison between Calculated and Measured Bed Load Transport Rates

The comparison between calculated and site-measured values of stream bed load transport rate is made on the basis of the following statistical criteria [3,15]:

• Root Mean Square Error (RMSE)
• Relative Error (RE) (%)
• Efficiency Coefficient EC (Nash and Sutcliffe, 1970) [16]
• Linear correlation coefficient r
• Determination coefficient r²
• Discrepancy ratio

The above mentioned statistical criteria values concerning Nestos River, for the case of manual calibration, are listed in

Table 1. Statistical criteria values of Nestos River (manual calibration).

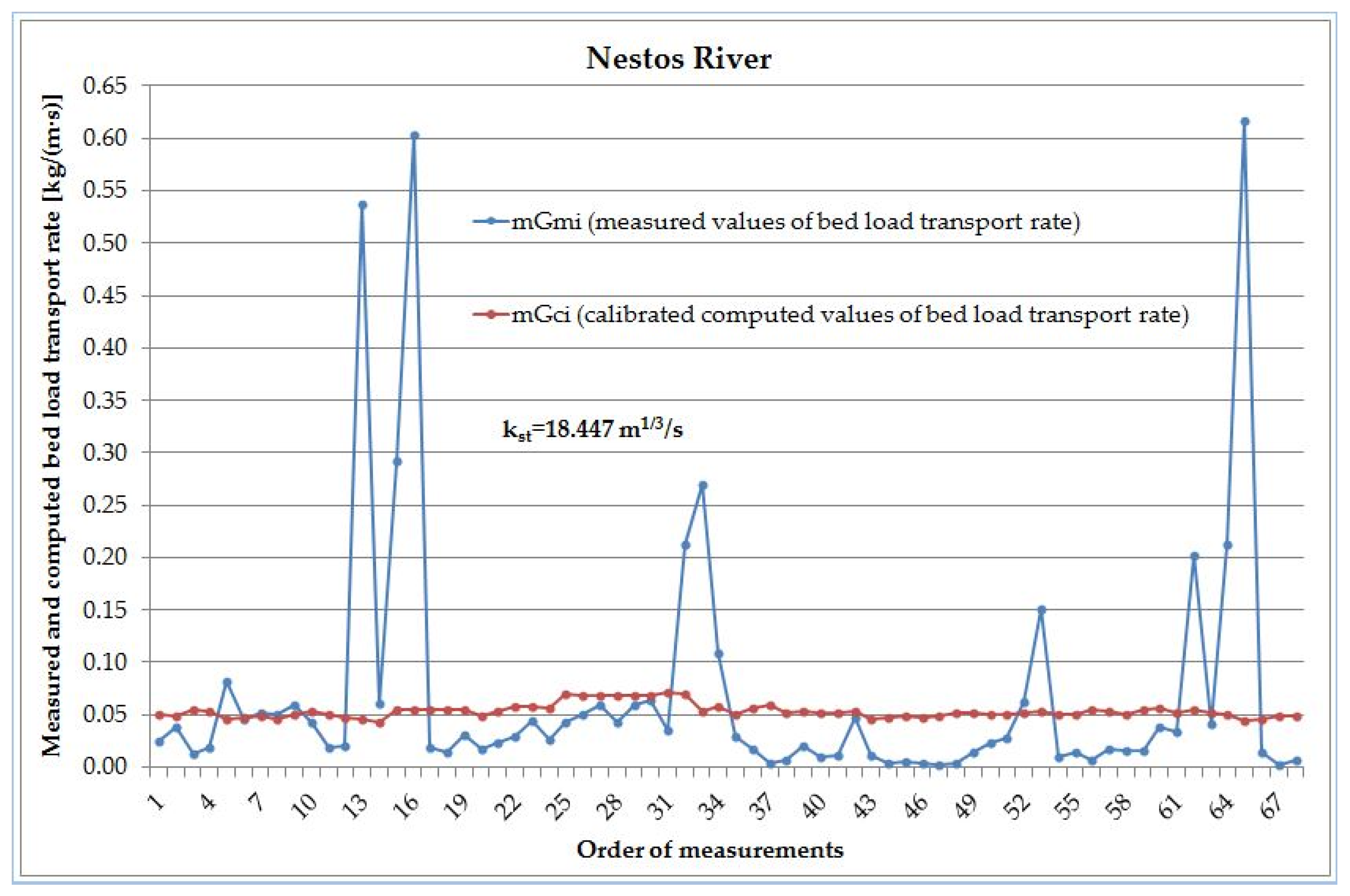
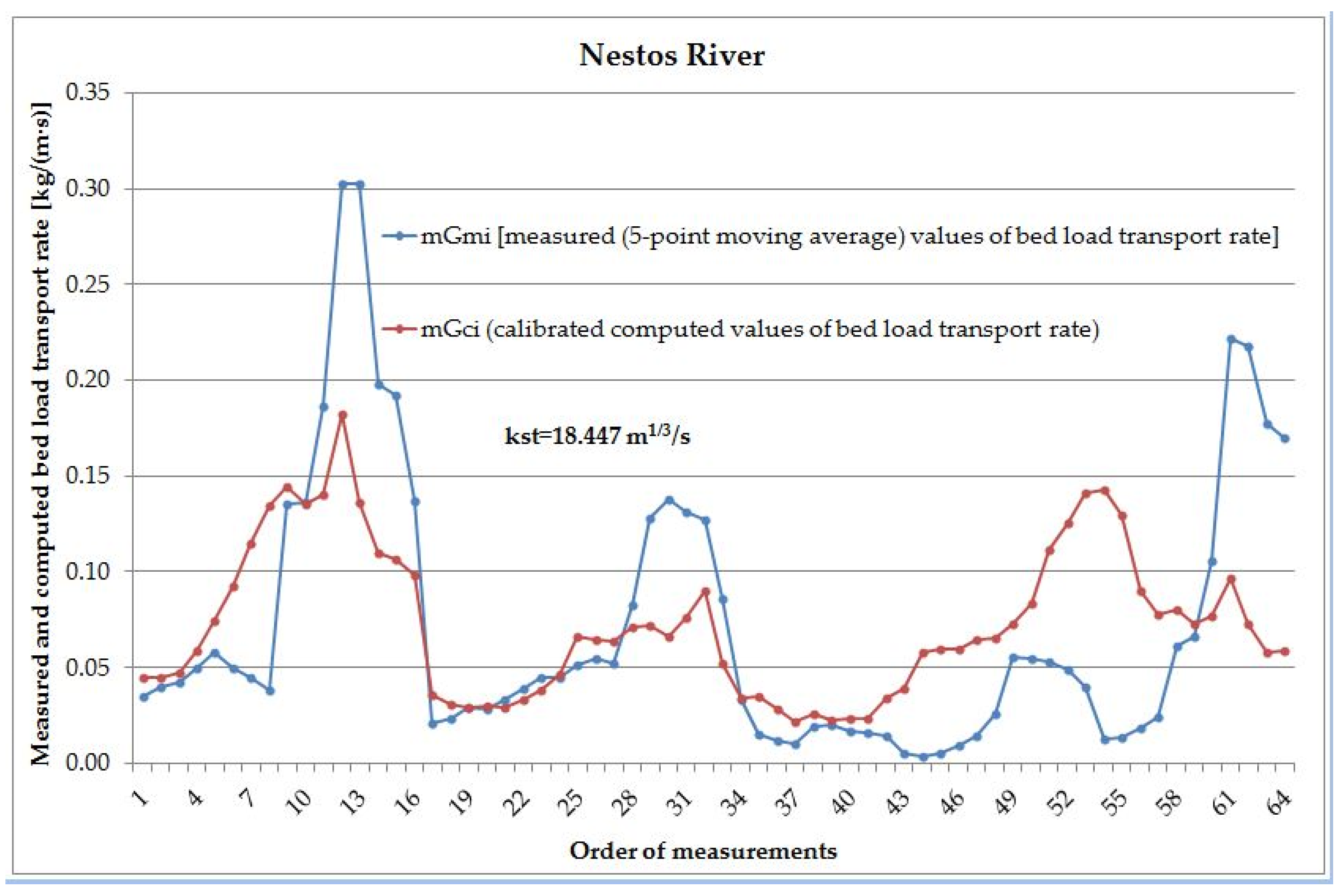
Number of Paired Values	RMSE	RE	EC	r	r2	Discrepancy Ratio
	(kg/(m·s))	(%)
68	0.0363	−8.6613	0.9171	0.9694	0.9397	1.0000

. It is noted that the relative error value depicted in Table 1, represents the average value of the relative errors calculated for each pair of calculated and site-measured bed load values.

In general, the obtained values of the statistical criteria RMSE, EC, r and r² for Nestos River can be considered fairly satisfactory. Additionally, the degree of linear dependence between calculated and measured bed load transport rate is very high.

In

Table 2. Statistical criteria values of Nestos River (optimization).

Number of Paired Values	RMSE	RE	EC	r	r2	Discrepancy Ratio
	(kg/(m·s))	(%)
68	0.1279	−2.6298	−0.0282	−0.0658	0.0043	0.3676

, the values of the statistical criteria used in the present study, for Nestos River and for the case of optimization, are shown.

The values of the statistical criteria for Nestos River, according to Table 2, are not satisfactory in comparison to the corresponding values of Table 1, except for the statistical criterion RE, which, in the case of optimization, obtains a more satisfactory value in comparison to the case of manual calibration.

In

Table 3. Statistical criteria values of Nestos River (5-point moving average measured values, optimization).

Number of Paired Values	RMSE	RE	EC	r	r2	Discrepancy Ratio
	(kg/(m·s))	(%)
64	0.0600	−1.2486	0.2957	0.5438	0.2957	0.6094

, the values of the statistical criteria used in the present study, for Nestos River and for the case of optimization, are given, where instead of the measured bed load values themselves, their 5-point moving averages are taken into account.

The values of the statistical criteria for Nestos River, according to Table 3, are not satisfactory in comparison to the corresponding values of Table 1, except for the statistical criterion RE, which, in the case of optimization, obtains a more satisfactory value in comparison to the case of manual calibration. However, the values of the statistical criteria, according to Table 3, are more satisfactory in comparison to the corresponding values of Table 2.

8. Discussion—Conclusions

An overall calibration of the Meyer-Peter and Müller formula [13] is presented on the basis of bed load measurements in a specific location of the Nestos River basin. In the present study, the optimization of the bed roughness coefficient is performed in a uniform manner for the whole range of the measured data after including at once all the available measured values of bed load transport rate. This calibration is contrasted to manual calibrations carried out on partial measurement sets. Similar attempts have been presented in relation to measurements in Kosynthos River and Kimmeria Torrent, two other streams of local importance [3]. The present approach is different in the sense of considering both parameters α and β defined above, simultaneously, while k_st was given a priori a constant realistic fixed value. This value is the average of the results of the above mentioned manual calibrations.

The differences between computed and measured bed load transport values followed the trend indicated in the literature [5], while consideration of moving averages instead of raw bed load measurements results in a much better adjustment of the Meyer-Peter and Müller model [13]. In this way, a different view of the simulating capacity of the model under study is given.