Distributed Strain Measurement Using Power-Based Brillouin Sensor with Three Folded Dynamic Range †
Abstract
:1. Introduction
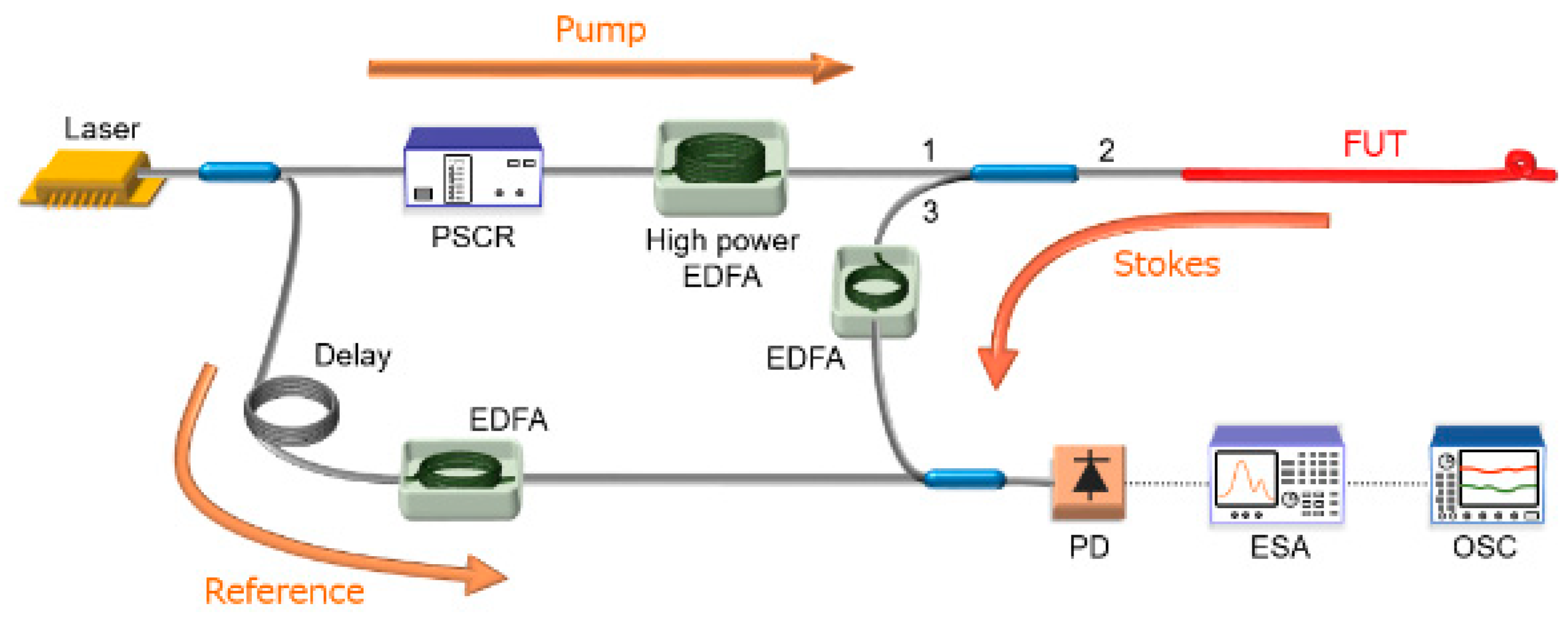
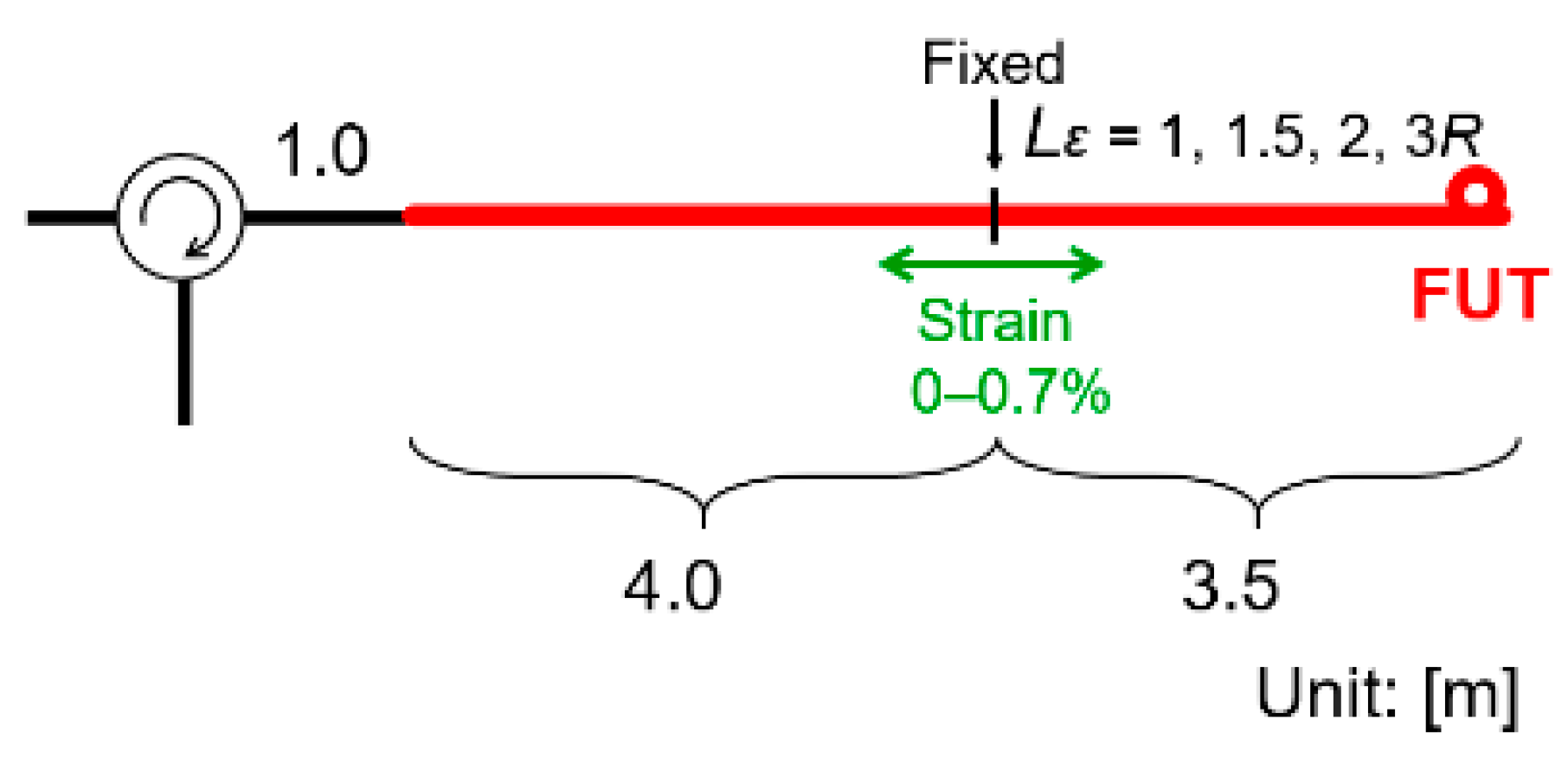
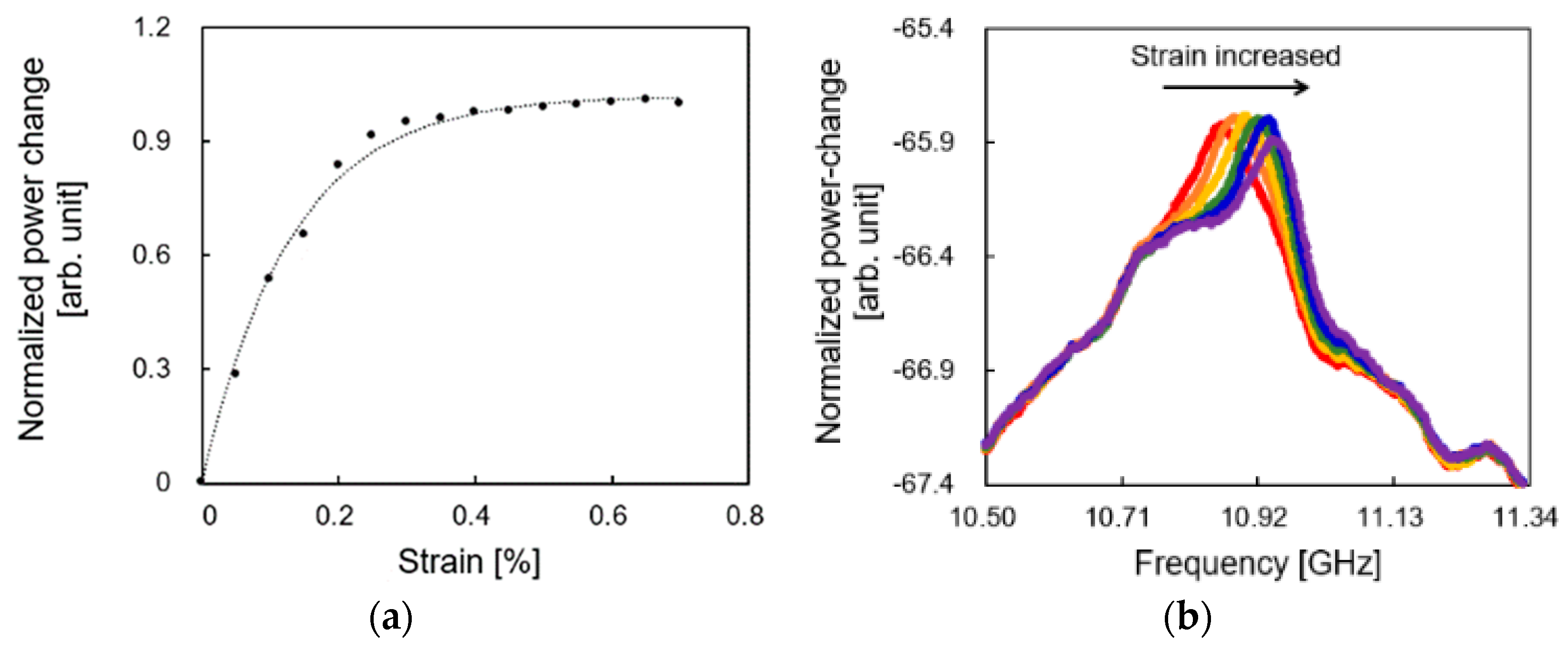
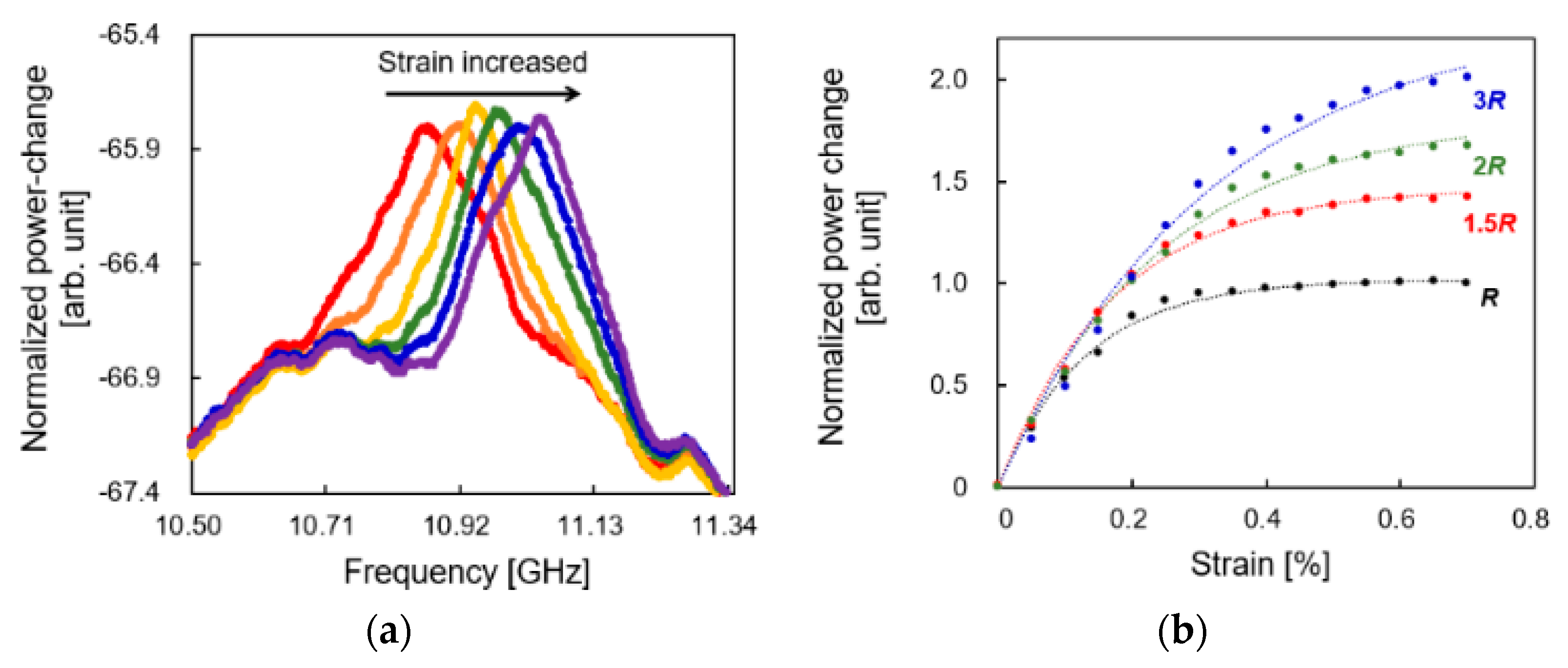
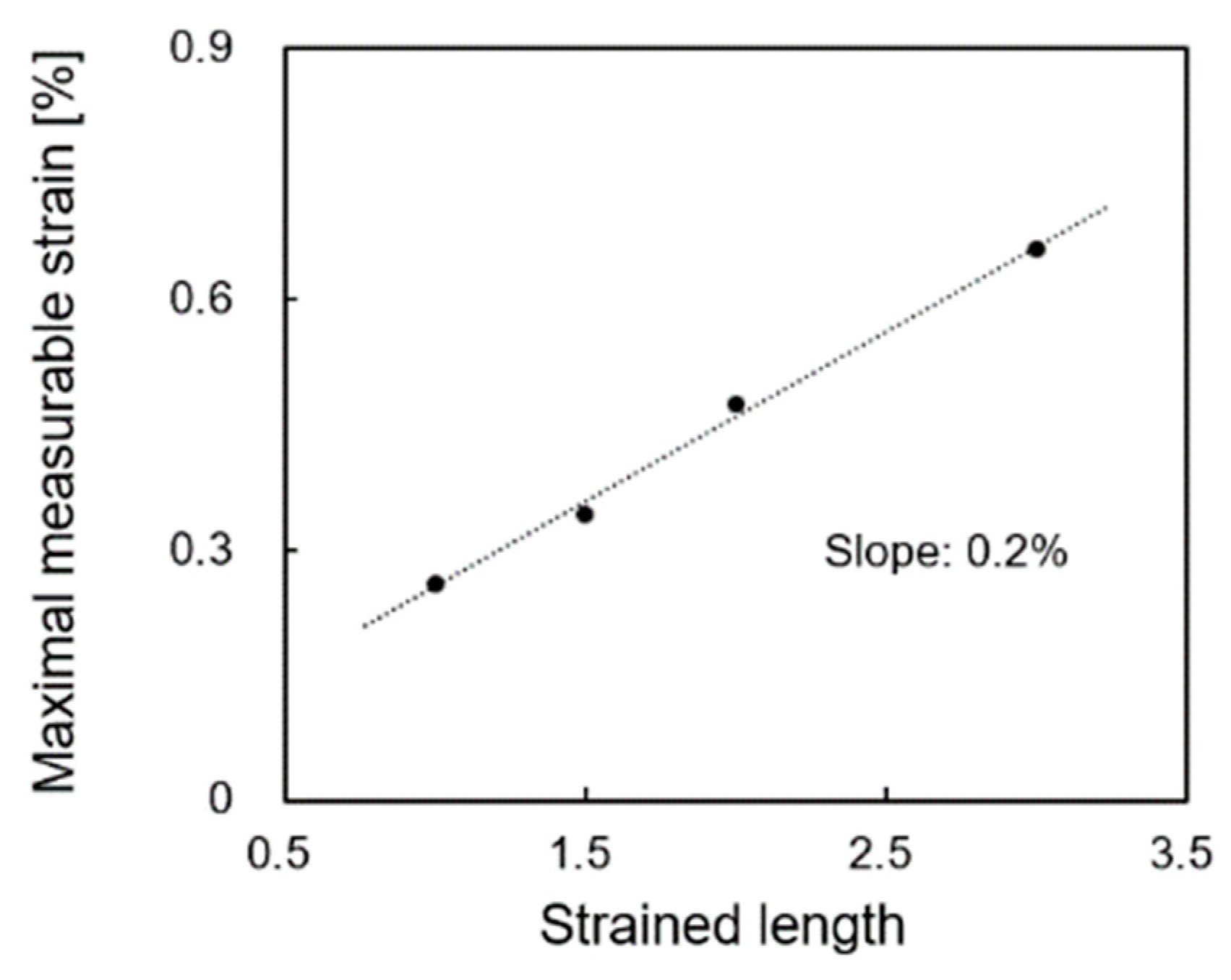
2. Experiments
3. Conclusions
Funding
Conflicts of Interest
References
- Lee, H.; Hayashi, N.; Mizuno, Y.; Nakamura, K. Slope-assisted Brillouin optical correlation-domain reflectometry: proof of concept. IEEE Photon. J. 2016, 8, 6802807. [Google Scholar] [CrossRef]
- Mizuno, Y.; Zou, W.; He, Z.; Hotate, K. Proposal of Brillouin optical correlation-domain reflectometry (BOCDR). Opt. Express 2008, 16, 12148–12153. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Hayashi, N.; Mizuno, Y.; Nakamura, K. Operation of slope-assisted Brillouin optical correlation-domain reflectometry: comparison of system output with actual frequency shift distribution. Opt. Express 2016, 24, 29190–29197. [Google Scholar] [CrossRef]
- Lee, H.; Mizuno, Y.; Nakamura, K. Measurement sensitivity dependencies on incident power and spatial resolution in slope-assisted Brillouin optical correlation-domain reflectometry. Sens. Actuator A: Phys. 2017, 268, 68–71. [Google Scholar] [CrossRef]
- Song, K.Y.; He, Z.; Hotate, K. Optimization of Brillouin optical correlation domain analysis system based on intensity modulation scheme. Opt. Express 2006, 14, 4256–4263. [Google Scholar] [CrossRef] [PubMed]
- Song, K.Y.; He, Z.; Hotate, K. Effects of intensity modulation of light source on Brillouin optical correlation domain analysis. J. Lightw. Technol. 2007, 25, 1238–1246. [Google Scholar] [CrossRef]
- Mizuno, Y.; Zou, W.; He, Z.; Hotate, K. Operation of Brillouin optical correlation-domain reflectometry: theoretical analysis and experimental validation. J. Lightw. Technol. 2010, 28, 3300–3306. [Google Scholar] [CrossRef]
- Hotate, K.; Hasegawa, T. Measurement of Brillouin gain spectrum distribution along an optical fiber using a correlation-based technique—proposal, experiment and simulation—. IEICE Trans. Electron. 2000, E83-C, 405–412. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Noda, K.; Mizuno, Y.; Nakamura, K. Distributed Strain Measurement Using Power-Based Brillouin Sensor with Three Folded Dynamic Range. Proceedings 2019, 15, 26. https://doi.org/10.3390/proceedings2019015026
Lee H, Noda K, Mizuno Y, Nakamura K. Distributed Strain Measurement Using Power-Based Brillouin Sensor with Three Folded Dynamic Range. Proceedings. 2019; 15(1):26. https://doi.org/10.3390/proceedings2019015026
Chicago/Turabian StyleLee, Heeyoung, Kohei Noda, Yosuke Mizuno, and Kentaro Nakamura. 2019. "Distributed Strain Measurement Using Power-Based Brillouin Sensor with Three Folded Dynamic Range" Proceedings 15, no. 1: 26. https://doi.org/10.3390/proceedings2019015026
APA StyleLee, H., Noda, K., Mizuno, Y., & Nakamura, K. (2019). Distributed Strain Measurement Using Power-Based Brillouin Sensor with Three Folded Dynamic Range. Proceedings, 15(1), 26. https://doi.org/10.3390/proceedings2019015026



