Dynamic Catadioptric Sensory Data Fusion for Visual Localization in Mobile Robotics †
Abstract
:1. Introduction
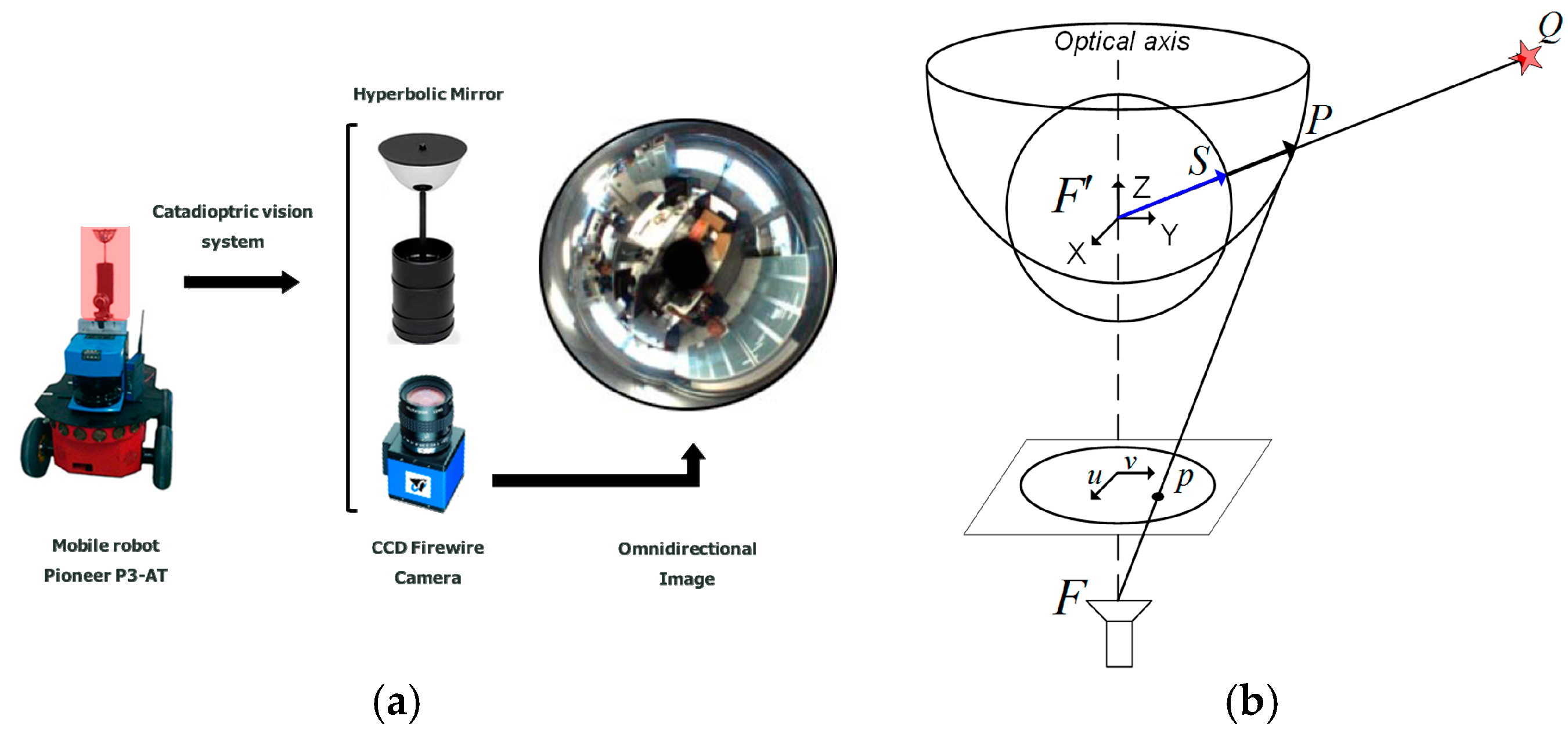
2. Catadioptric Sensor
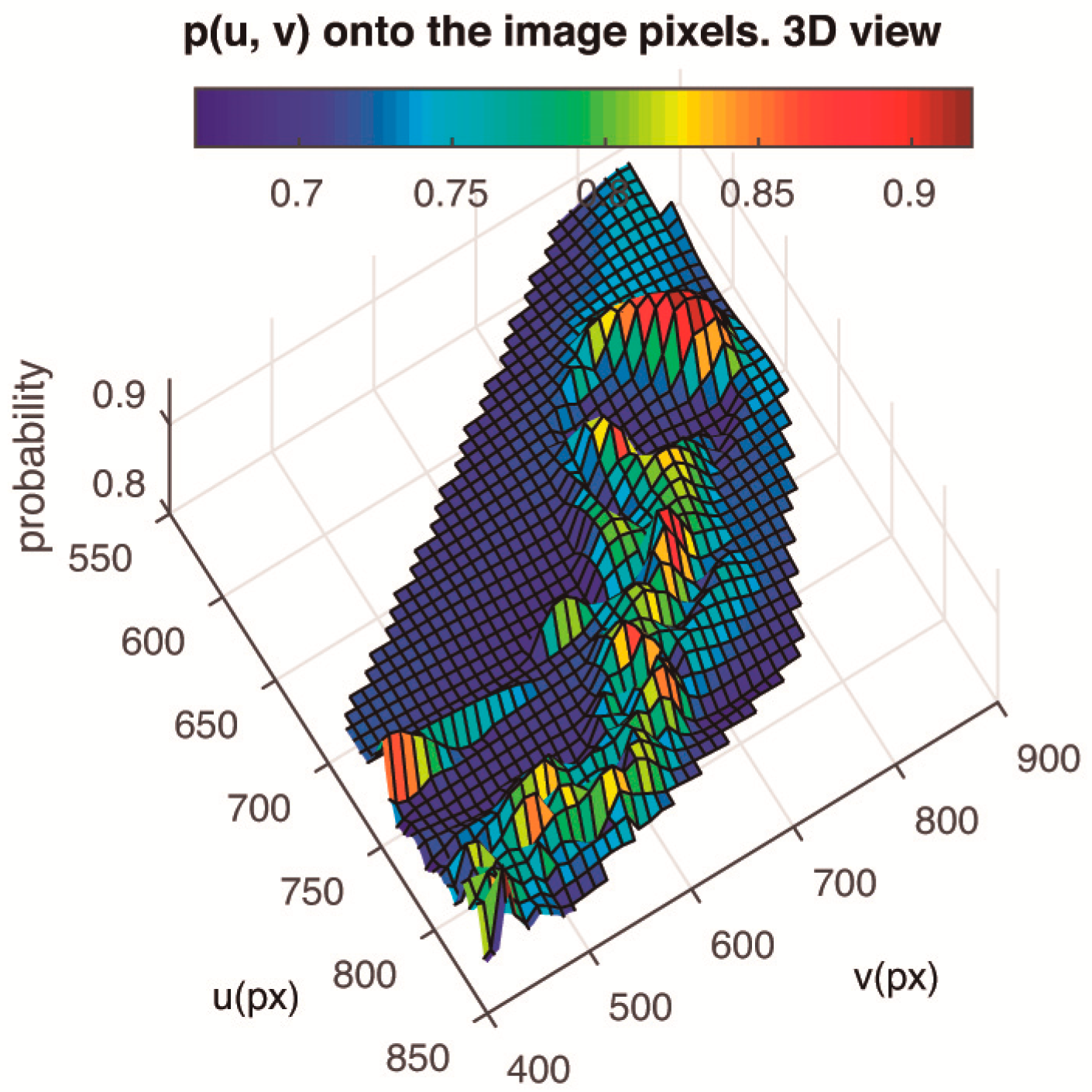
3. Dynamic Matching
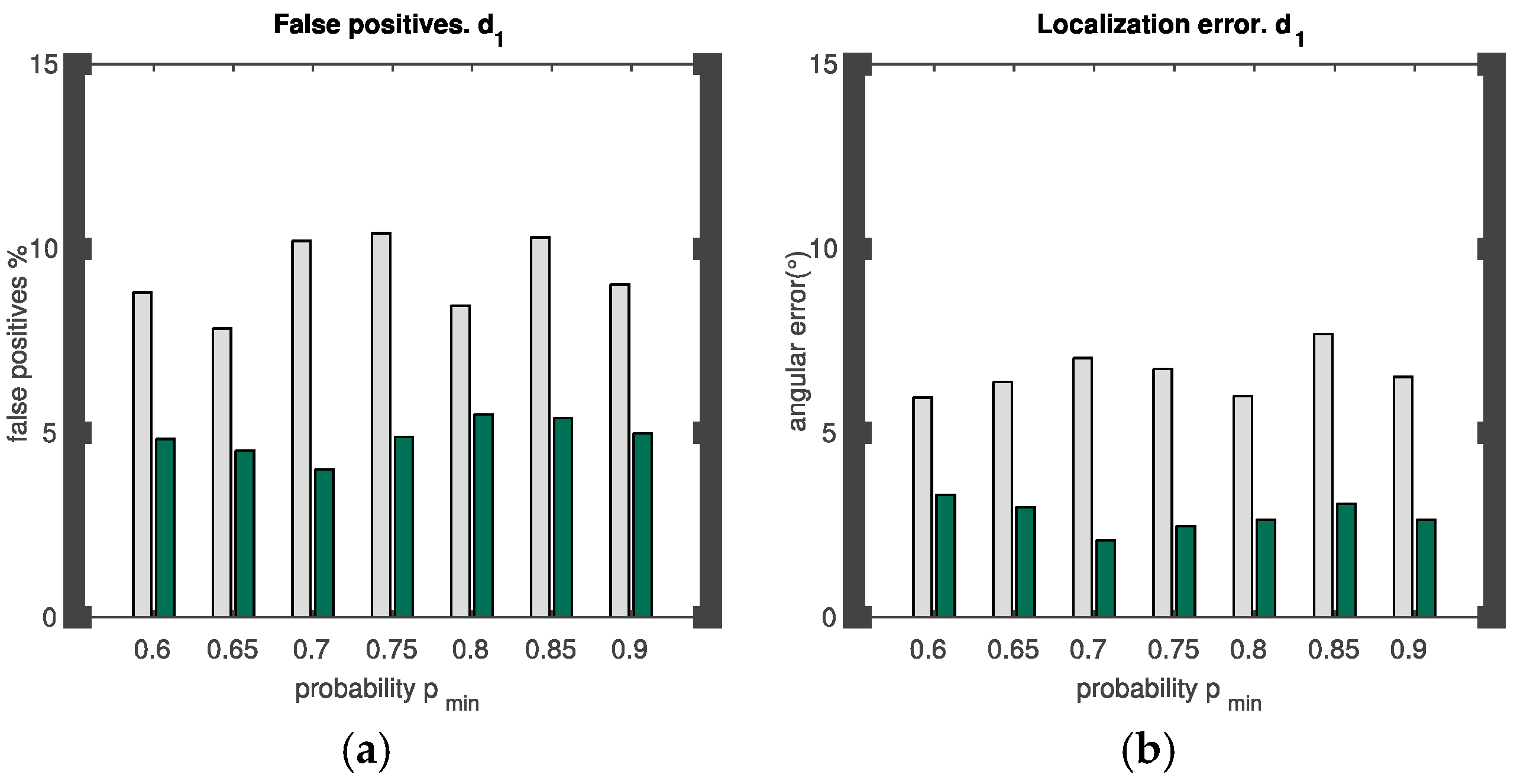
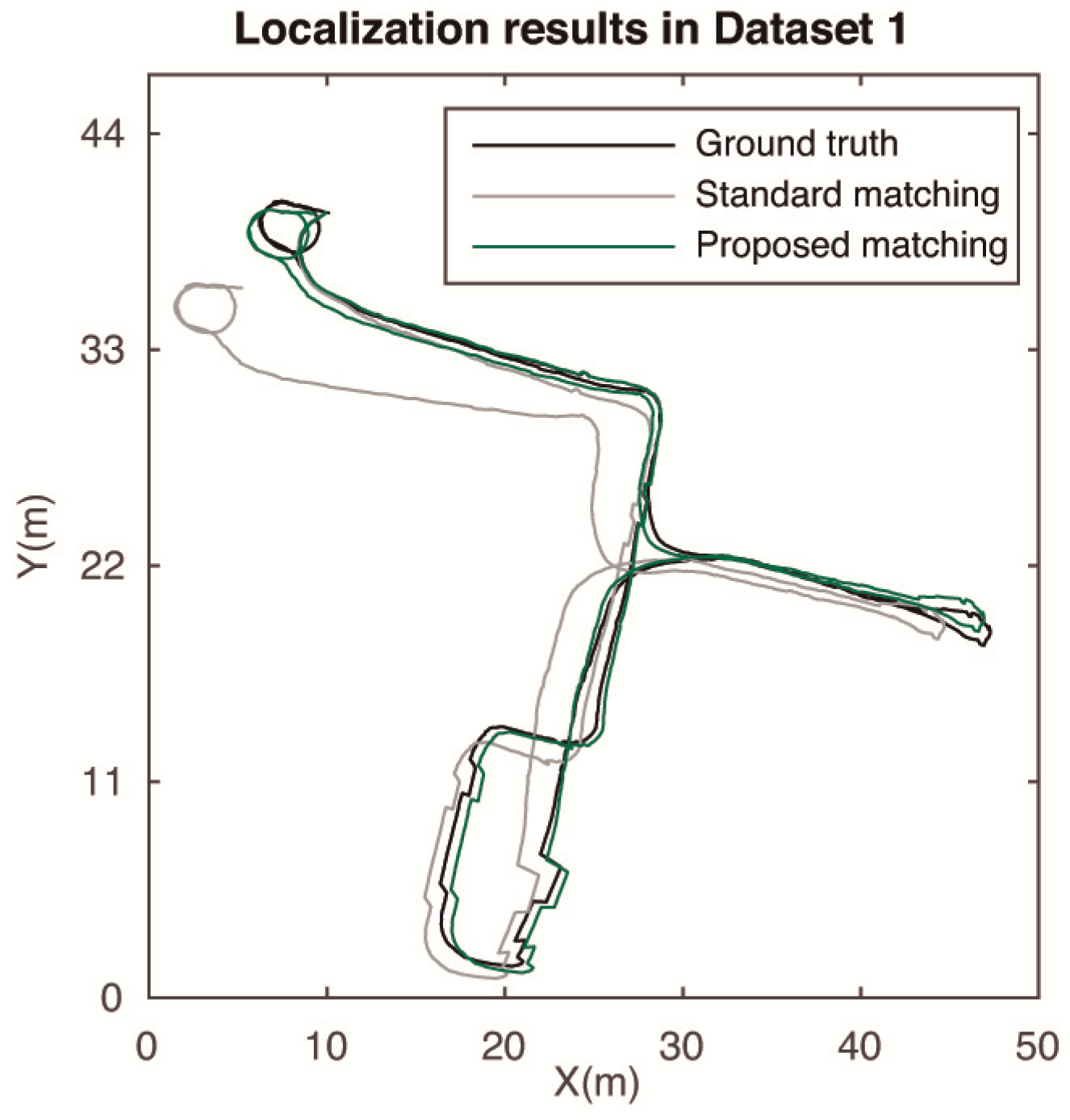
4. Experiments
Author Contributions
Funding
Conflicts of Interest
References
- Valiente, D.; Gil, A.; Payá, L.; Sebastián, J.M.; Reinoso, O. Robust visual localization with dynamic uncertainty management in omnidirectional SLAM. Appl. Sci. 2017, 7, 1294. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Speeded up robust features. Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Huang, S.; Dissanayake, G. Convergence and Consistency Analysis for Extended Kalman Filter Based SLAM. IEEE Trans. Rob. 2007, 23, 1036–1049. [Google Scholar] [CrossRef]
- Kulback, S.; Leiber, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Rasmussen, C.; Hager, G.D. Probabilistic data association methods for tracking complex visual objects. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 560–576. [Google Scholar] [CrossRef]
- Valiente, D.; Gil, A.; Fernández, L.; Reinoso, Ó. Visual SLAM Based on Single Omnidirectional Views. In Informatics in Control, Automation and Robotics: 9th International Conference, ICINCO 2012, Rome, Italy, 28–31 July 2012 Revised Selected Papers; Springer: Berlin/Heidelberg, Germany, 2014; pp. 131–146. [Google Scholar]
- ARVC: Automation, Robotics and Computer Vision Research Group. Miguel Hernandez University. Omnidiectional Image Dataset at Innova Building. Available online: http://arvc.umh.es/db/images/innova_trajectory/ (accessed on 11 January 2019).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valiente, D.; Payá, L.; Sebastián, J.M.; Jiménez, L.M.; Reinoso, O. Dynamic Catadioptric Sensory Data Fusion for Visual Localization in Mobile Robotics. Proceedings 2019, 15, 2. https://doi.org/10.3390/proceedings2019015002
Valiente D, Payá L, Sebastián JM, Jiménez LM, Reinoso O. Dynamic Catadioptric Sensory Data Fusion for Visual Localization in Mobile Robotics. Proceedings. 2019; 15(1):2. https://doi.org/10.3390/proceedings2019015002
Chicago/Turabian StyleValiente, David, Luis Payá, José M. Sebastián, Luis M. Jiménez, and Oscar Reinoso. 2019. "Dynamic Catadioptric Sensory Data Fusion for Visual Localization in Mobile Robotics" Proceedings 15, no. 1: 2. https://doi.org/10.3390/proceedings2019015002
APA StyleValiente, D., Payá, L., Sebastián, J. M., Jiménez, L. M., & Reinoso, O. (2019). Dynamic Catadioptric Sensory Data Fusion for Visual Localization in Mobile Robotics. Proceedings, 15(1), 2. https://doi.org/10.3390/proceedings2019015002







