Quark Number Susceptibilities and Equation of State in QCD at Finite μB †
Abstract
:1. Introduction
2. Calculational Details
3. Results
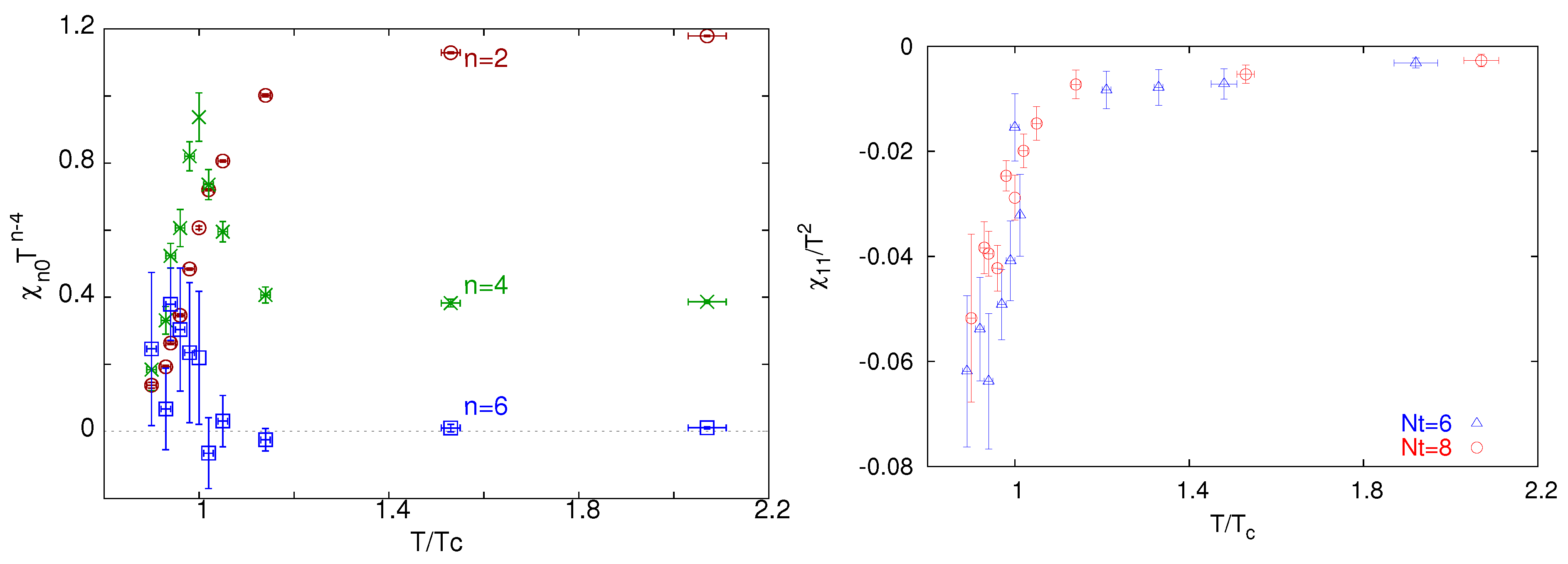
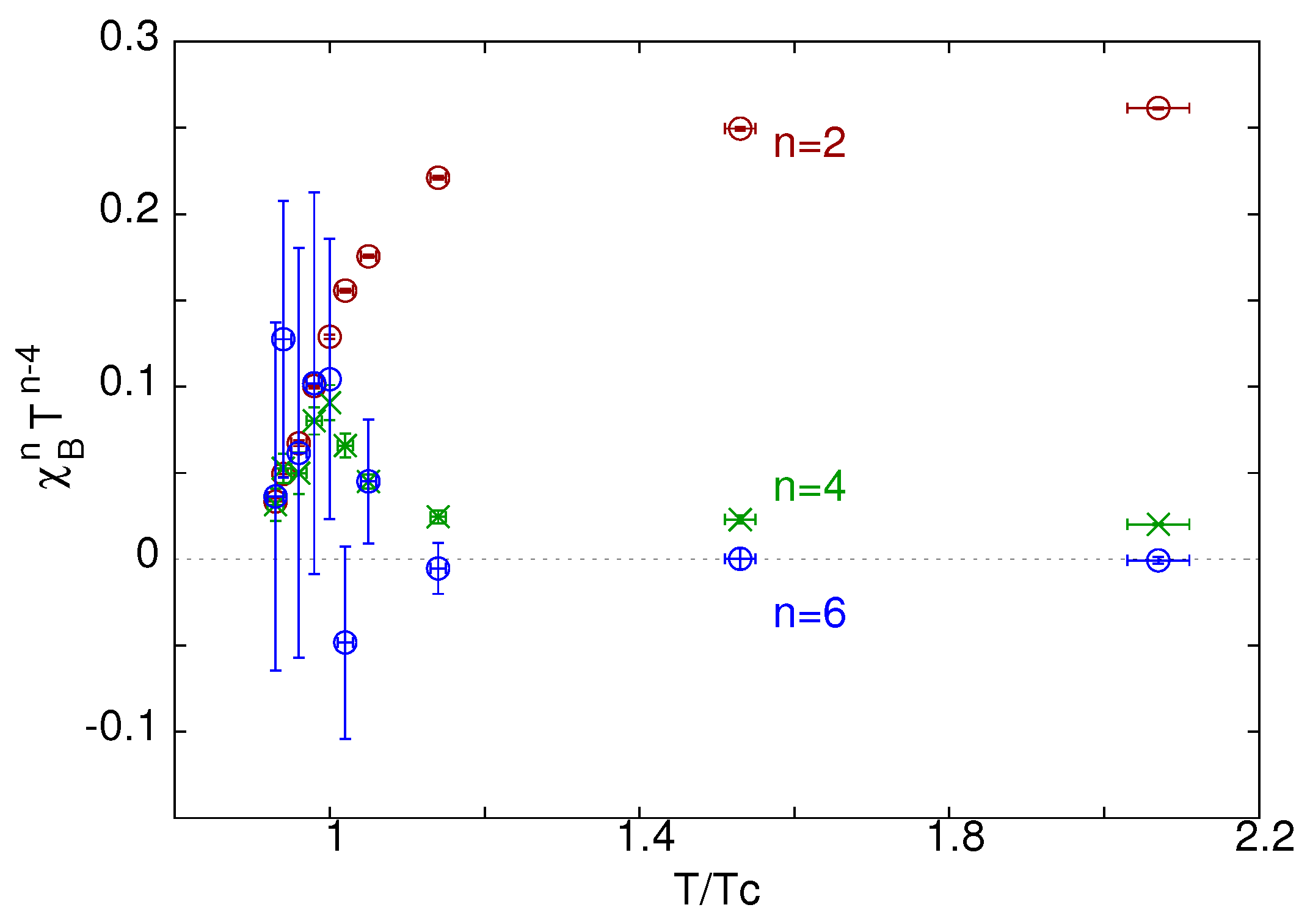
3.1. Quark Number Susceptibilities
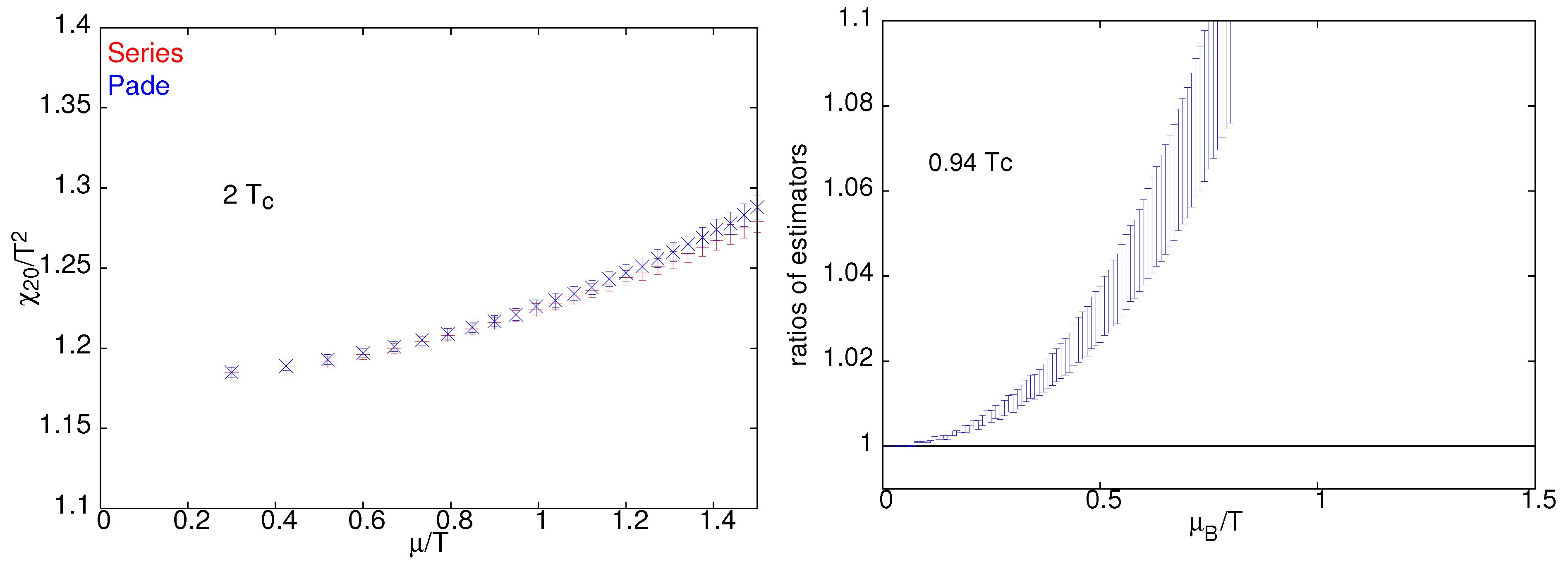
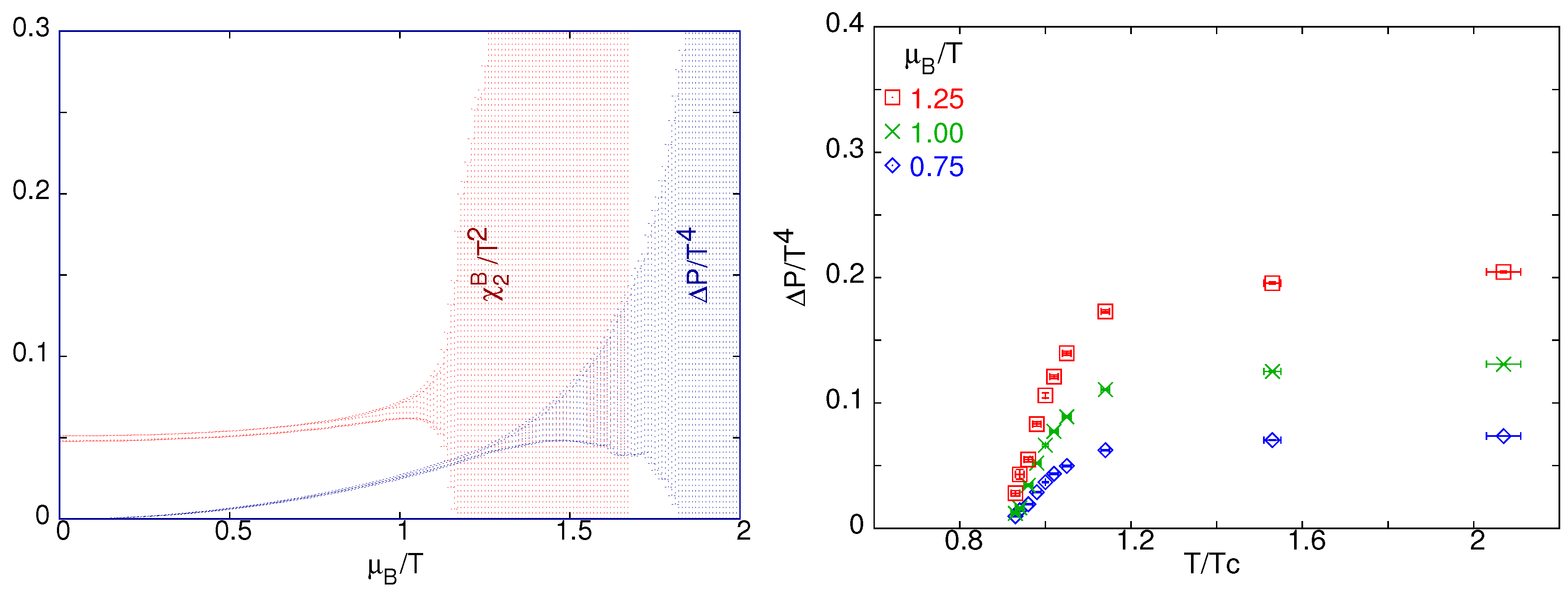
3.2. Equation of State at Finite
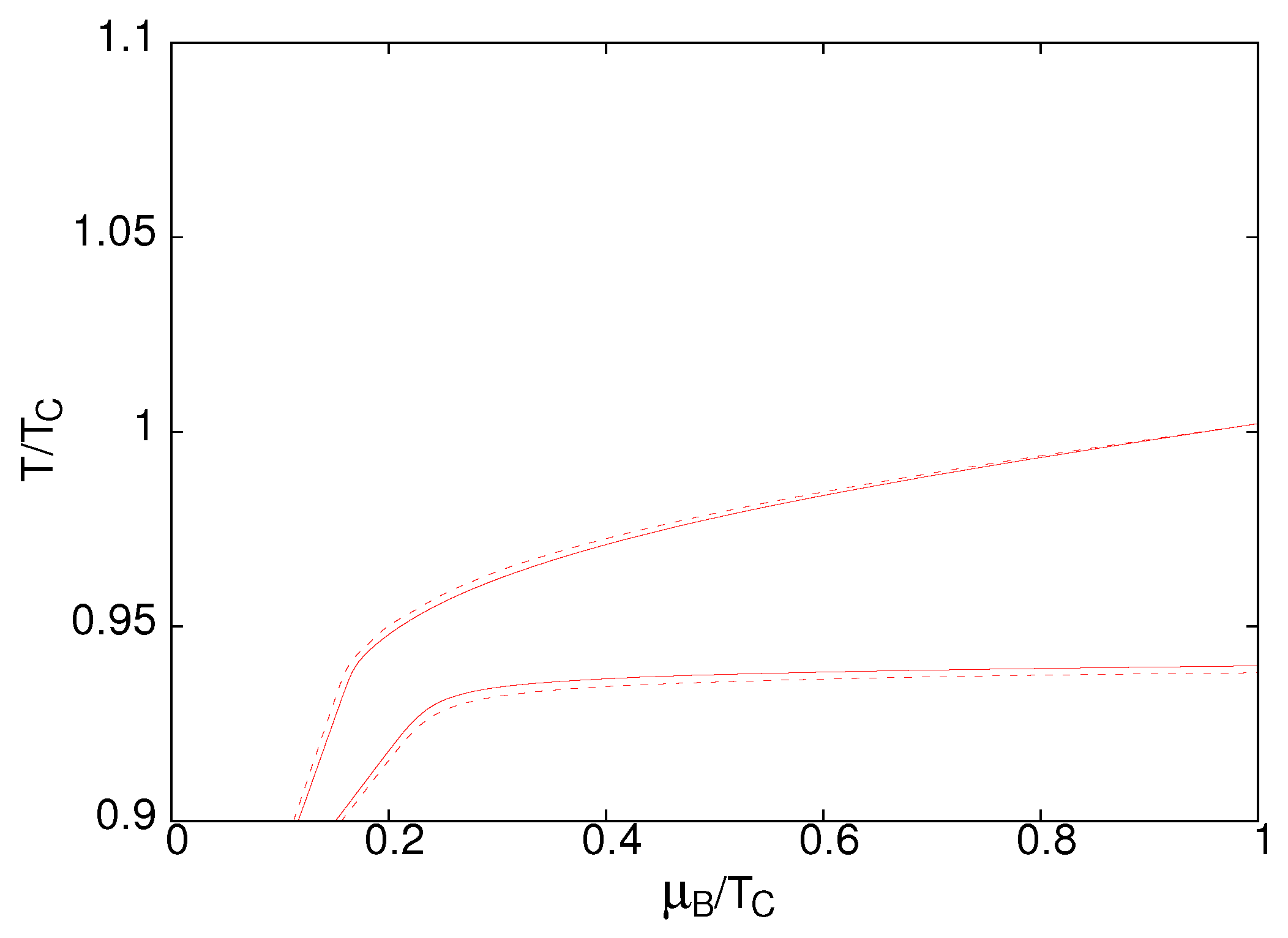
3.3. Fluctuations and Freezeout
4. Summary and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| QCD | quantum chromodynamics |
| QGP | Quark-gluon plasma |
| BNS | Baryon number susceptibilities |
| QNS | Quark number susceptibilities |
| FAIR | Facility for antiproton and Ion Research |
| RHIC | Relativistic Heavy Ion Collider |
| CBM | Cold Baryonic Matter |
| BES | Beam energy scan |
| LHC | Large Hadron Collider |
References
- Gavai, R.V.; Gupta, S.; Ray, R. Taylor expansions in chemical potential. Prog. Theor. Phys. Suppl. 2004, 153, 270. [Google Scholar] [CrossRef]
- Ejiri, S.; Allton, C.R.; Hands, S.J.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Schmidt, C. Study of QCD thermodynamics at finite density by Taylor expansion. Prog. Theor. Phys. Suppl. 2004, 153, 118. [Google Scholar] [CrossRef]
- Datta, S.; Gavai, R.V.; Gupta, S. Quark number susceptibilities and equation of state at finite chemical potential in staggered QCD with Nt = 8. Phys. Rev. D 2017, 95, 054512. [Google Scholar]
- Gavai, R.V.; Gupta, S. QCD at finite chemical potential with six time slices. Phys. Rev. D 2008, 78, 114503. [Google Scholar]
- Gottlieb, S.A.; Liu, W.; Toussaint, D.; Renken, R.L.; Sugar, R.L. Hybrid Molecular Dynamics Algorithms for the Numerical Simulation of Quantum Chromodynamics. Phys. Rev. D 1987, 35, 2531. [Google Scholar]
- Borsányi, S.; Durr, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Kurth, T.; Lellouch, L.; Lippert, T.; Mcneile, C.; et al. High-precision scale setting in lattice QCD. JHEP 2012, 1209, 010. [Google Scholar]
- Gavai, R.V.; Gupta, S. The Critical end point of QCD. Phys. Rev. D 2005, 71, 114014. [Google Scholar]
- Gottlieb, S.A.; Liu, W.; Toussaint, D.; Renken, R.L.; Sugar, R.L. The Quark Number Susceptibility of High Temperature QCD. Phys. Rev. Lett. 1987, 59, 2247. [Google Scholar]
- Gupta, S.; Karthik, N.; Majumdar, P. On criticality and the equation of state of QCD at finite chemical potential. Phys. Rev. D 2014, 90, 034001. [Google Scholar]
- Andersen, J.O.; Mogliacci, S.; Su, N.; Vuorinen, A. Quark number susceptibilities from resummed perturbation theory. Phys. Rev. D 2013, 87, 074003. [Google Scholar]
- Haque, N.; Mustafa, M.G.; Strickland, M. Quark Number Susceptibilities from Two-Loop Hard Thermal Loop Perturbation Theory. JHEP 2013, 1307, 184. [Google Scholar]
- Datta, S.; Gavai, R.V.; Gupta, S. QCD at finite chemical potential with Nt = 8. PoS Lattice 2014, 2013, 202. [Google Scholar]
- Gavai, R.V.; Gupta, S. Simple patterns for non-linear susceptibilities near Tc. Phys. Rev. D 2005, 72, 054006. [Google Scholar]
- Ejiri, S.; Karsch, F.; Redlich, K. Hadronic fluctuations at the QCD phase transition. Phys. Lett. B 2006, 633, 275. [Google Scholar]
- Koch, V.; Majumdar, A.; Randrup, J. Baryon-strangeness correlations: A Diagnostic of strongly interacting matter. Phys. Rev. Lett. 2005, 95, 182301. [Google Scholar]
- Gavai, R.; Gupta, S. Fluctuations, strangeness and quasi-quarks in heavy-ion collisions from lattice QCD. Phys. Rev. D 2006, 73, 014004. [Google Scholar]
- Bazavov, A.; Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Maezawa, Y.; Mukherjee, S.; Ohno, H.; Petreczky, P.; et al. The QCD equation of state to from Lattice QCD. Phys. Rev. D 2017, 95, 054504. [Google Scholar]
- DÉlia, M.; Gagliardi, G.; Sanfilippo, F. Higher order quark number fluctuations via imaginary chemical potentials in Nf = 2 + 1 QCD. Phys. Rev. D 2017, 95, 094503. [Google Scholar]
- Vovchenko, V.; Steinheimer, J.; Philipsen, O.; Stoecker, H. Cluster Expansion Model for QCD Baryon Number Fluctuations: No Phase Transition at μB/T < π. Phys. Rev. D 2018, 97, 114030. [Google Scholar]
- Fodor, Z.; Giordano, M.; Guenther, J.N.; Kapas, K.; Katz, S.D.; Pasztor, A.; Portillo, I.; Ratti, C.; Sexty, D.; Szabo, K.K. Searching for a CEP signal with lattice QCD simulations. arXiv 2018, arXiv:1807.09862. [Google Scholar]
- Gavai, R.; Gupta, S. Lattice QCD predictions for shapes of event distributions along the freezeout curve in heavy-ion collisions. Phys. Lett. B 2011, 696, 459. [Google Scholar]
- Gupta, S. Finding the critical end point of QCD: Lattice and experiment. PoS CPOD 2009, 2009, 025. [Google Scholar]
- Bazavov, A.; Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Mukherjee, S.; Petreczky, P.; Schmidt, C.; Smith, D.; et al. Freeze-out Conditions in Heavy Ion Collisions from QCD Thermodynamics. Phys. Rev. Lett. 2012, 109, 192302. [Google Scholar]
- Borsányi, S.; Fodor, Z.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. Freeze-out parameters: Lattice meets experiment. Phys. Rev. Lett. 2013, 111, 062005. [Google Scholar]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.D.; Aparin, A.; Arkhipkin, D.; et al. Energy Dependence of Moments of Net-proton Multiplicity Distributions at RHIC. Phys. Rev. Lett. 2014, 112, 032302. [Google Scholar]
- Petran, M.; Letessier, J.; Petráček, V.; Rafelski, J. Hadron production and quark-gluon plasma hadronization in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. C 2013, 88, 034907. [Google Scholar] [CrossRef]
- Becattini, F.; Steinheimer, J.; Stock, R.; Bleicher, M. Hadronization conditions in relativistic nuclear collisions and the QCD pseudo-critical line. Phys. Lett. B 2017, 764, 241. [Google Scholar]
- Petreczky, P. Lattice QCD at non-zero temperature. J. Phys. G 2012, 39, 093002. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Datta, S.; Gavai, R.V.; Gupta, S. Quark Number Susceptibilities and Equation of State in QCD at Finite μB. Proceedings 2019, 13, 5. https://doi.org/10.3390/proceedings2019013005
Datta S, Gavai RV, Gupta S. Quark Number Susceptibilities and Equation of State in QCD at Finite μB. Proceedings. 2019; 13(1):5. https://doi.org/10.3390/proceedings2019013005
Chicago/Turabian StyleDatta, Saumen, Rajiv V. Gavai, and Sourendu Gupta. 2019. "Quark Number Susceptibilities and Equation of State in QCD at Finite μB" Proceedings 13, no. 1: 5. https://doi.org/10.3390/proceedings2019013005
APA StyleDatta, S., Gavai, R. V., & Gupta, S. (2019). Quark Number Susceptibilities and Equation of State in QCD at Finite μB. Proceedings, 13(1), 5. https://doi.org/10.3390/proceedings2019013005



