Analysis of Spot Response Temperature Fields in Microfluidic Systems: Analogy with the “Heart of Voh” ^†

Abstract

The “Heart of Voh”, immortalized by Yann Arthus Bertrand in his book The Earth from the Air, depicts a sparse, heart-shaped clearing in the mangroves of New Caledonia. This highly poetic image is also the physical representation of thermal diffusion phenomena disrupted by fluid flow. This type of figure is a basic figure for analyzing source fields in a microfluidic channel surrounded by solid walls. Here, several analytical solutions will be presented and used for the estimation of crucial parameters related to the thermal diffusivity of the walls around the channel and the fluid flow inside the channel.

1. Introduction

The “Heart of Voh” (see Figure 1) is a highly poetic image immortalized by Yann Arthus Bertrand in his book The Earth from the Air [1]. It depicts a sparse, heart-shaped clearing in the mangroves of New Caledonia. This type of figure is a basic figure for analyzing source fields in a microfluidic channel surrounded by solid walls. In particular, a source point response in a micro-channel in steady or transient conditions is the Green function, which then allows the thermal response of any source field in or around a micro-channel to be calculated using a convolution product. We have studied this type of source in microchannels to determine source terms of chemical reactions (see [2]) but with methods consisting of Laplacians of temperature fields, which are sensitive to measurement noise and which do not allow for an in-depth analysis of transfers. Here, we propose revisiting the treatment of these temperature fields using more precise analytical solutions to the direct problem, by considering Fourier transforms of these temperature fields (see [3]). These methods also allow us to develop methods for estimating a certain number of parameters related to flow and diffusion in the walls.

We will describe here the solutions to the direct problem, the associated experiments, and then some estimation methods.

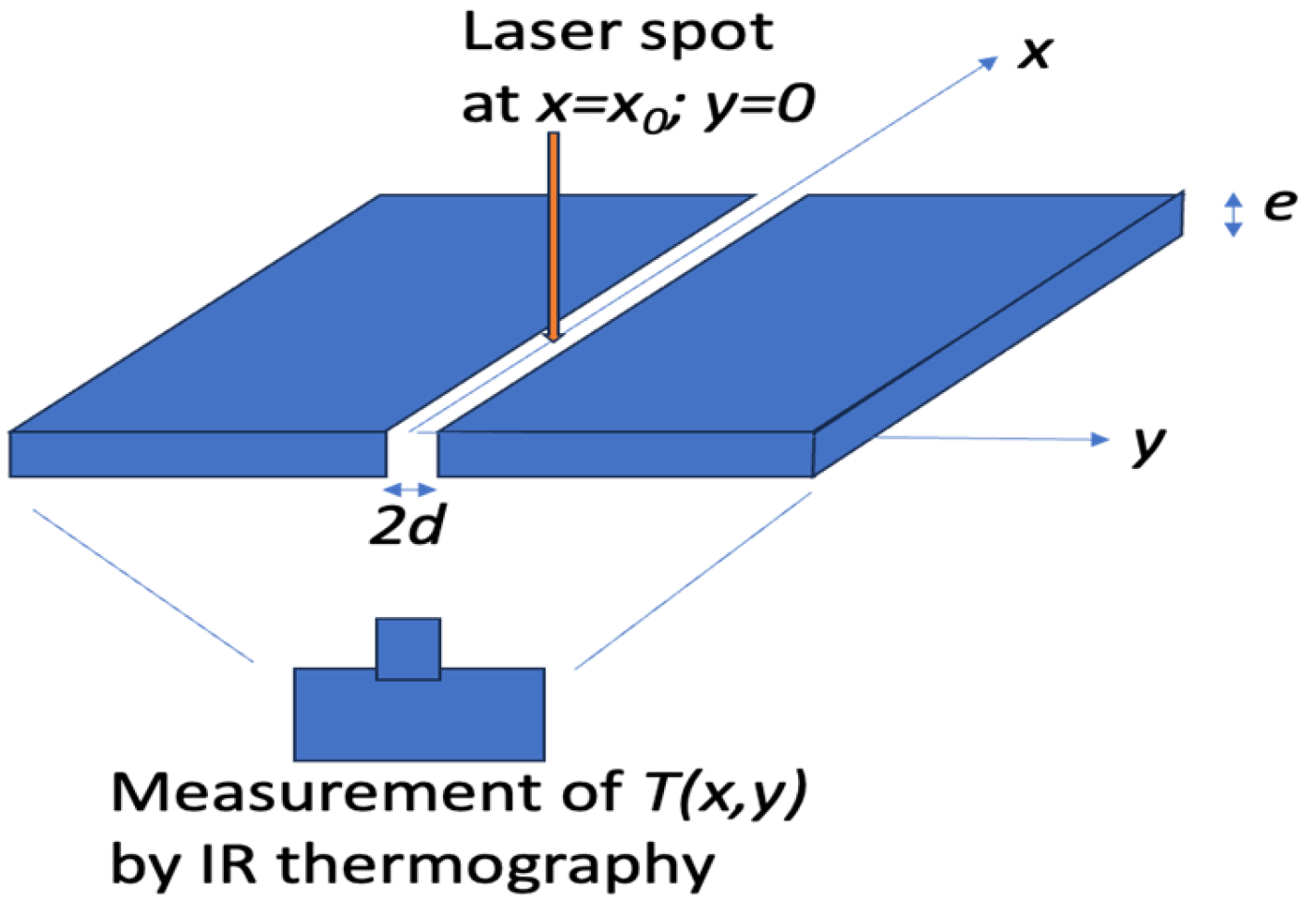
2. Analytical Solutions to the Forward Problem

A microfluidic chip consisting of a plate of thickness e crossed by a channel of width 2d (see Figure 2) is considered here. Thanks to the symmetry with respect to Ox, only the problem related to the half-plane Ox,y is considered. The flow in the channel with a flow velocity V is uniformly considered. In order to study the Green function, a stationary point heat source Q (in W) is placed in x = x₀. It is assumed that the temperature of the fluid $T_0$ only depends on x. For reasons of simplicity, it is assumed here that the thermal conductivity λ of the water in the channel is the same as that of the contacting walls. The lateral convective losses are represented by an exchange coefficient h. Finally, the loss term distributed along x is represented by a surface density of heat flux f(x) in relation to a boundary condition of the diffusion problem in the plate.

We can then write the balance of heat transfers in the channel in contact with the plate as Expression (1), and the 2D diffusion problem in the plate as Expression (2):

$${\displaystyle \frac{V}{a}}{\displaystyle \frac{d{T}_0}{dx}}={\displaystyle \frac{d^2{T}_0}{{dx}^2}}-{\displaystyle \frac{2h}{\lambda e}}{T}_0+{\displaystyle \frac{Q}{\lambda e}}\delta \left(x-x_0\right)-{\displaystyle \frac{f\left(x\right)}{\lambda e}}$$

(1)

$${\displaystyle \frac{{𝜕}^{2}T}{{𝜕x}^2}}+{\displaystyle \frac{{𝜕}^{2}T}{{𝜕y}^2}}-{\displaystyle \frac{2h}{\lambda e}}T=0$$

(2)

It is assumed that the length L along Ox of the plate is large compared to the characteristic dimension linked to convective losses, such as $L\gg \sqrt{{\displaystyle \frac{\lambda e}{2h}}}$.

The boundary conditions are as follows:

At x = 0 and x = L, T₀(0) = T(x = 0,y) = 0 and T₀(L) = T(x = L,y) = 0

At y = 0 ${\left.-\lambda \left[{\displaystyle \frac{𝜕T}{𝜕y}}\right.\right]}_{y=0,x}=f(x)$

At $y\to \mathrm{\infty }$ $T\left(x,\mathrm{\infty }\right)=0$

We can then consider a Fourier transformation along x, such that

$$\theta \left({\omega }_n,y\right)={\int }_0^{L}T\left(x,y\right)\exp \left(-j{\omega }_{n}x\right)dx$$

(3)

with ${\omega }_n=\mathrm{n}\mathsf{\pi }/\mathrm{L}$.

This then yields the following:

$${\theta }_0\left({\omega }_n\right)={\displaystyle \frac{Q \exp (-j{\omega }_n{x}_0)}{\lambda de\left(\frac{jV{\omega }_n}{a}+ {{\omega }_n}^2+\frac{2h}{\lambda e}+\frac{1}{e} \sqrt{{{\omega }_n}^2+\frac{2h}{\lambda e}}\right)}}$$

(4)

$$\theta \left({\omega }_n,y\right)={\theta }_0\left({\omega }_n\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-\sqrt{{{\omega }_n}^2+{\displaystyle \frac{2h}{\lambda e}}} y\right)$$

The temperature field depending on the x,y coordinates is then obtained with an inverse Fourier transform. This type of expression, and therefore this form of heart, depends only on three dimensionless parameters: a Nusselt number, Nu; a Peclet number, Pe; and a dimension ratio, L*, such as

$$Nu={\displaystyle \frac{2h}{\lambda e}}{L}^2; Pe={\displaystyle \frac{VL}{a}} \mathrm{and} L^{*}={\displaystyle \frac{L}{e}}$$

One example of a calculation result is given in Figure 3.

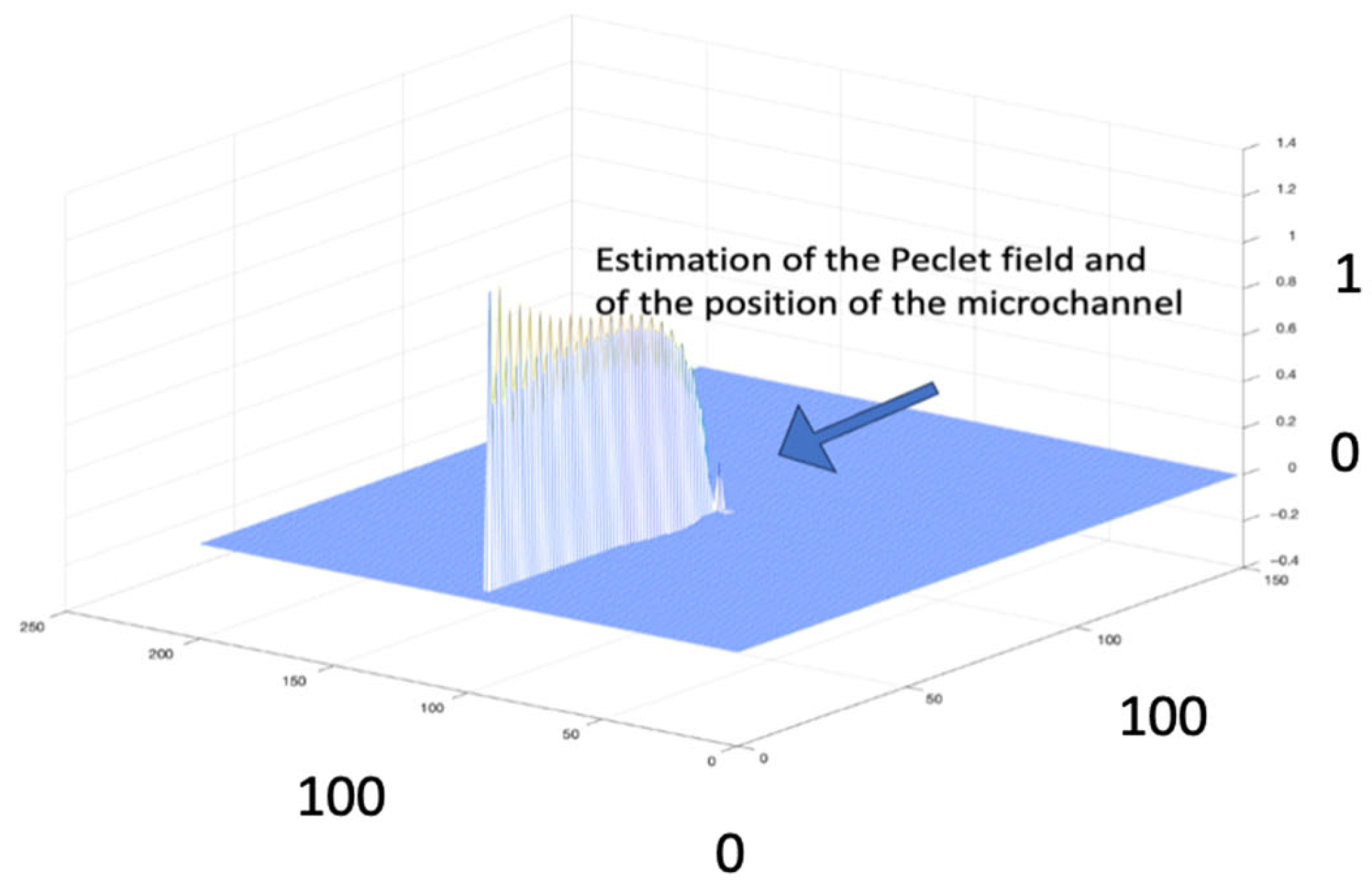
3. Considerations of Experimentation and Inversion

Implementing the direct problem has several advantages. First, the use of integral transformations (here, Fourier transformations) is convenient for revealing the main parameters of the problem and studying the inversion process. The small number of parameters can facilitate the implementation of an inverse method.

This type of approach provides an alternative to considering Laplacians or gradients of temperature fields, previously used in [2], which are highly sensitive to measurement noise.

For example, the comparison between the Fourier temperature field without flow ${\theta }_{01}\left({\omega }_n\right)$ and the Fourier temperature field with flow ${\theta }_{02}\left({\omega }_n\right)$ gives a suitable expression for the inversion, such as the following expression and results on Figure 4:

$$\mathit{P}\mathit{e}={\displaystyle \frac{\left({{\mathit{\omega }}_n^{*}}^2+Nu\right)({\mathit{\theta }}_{\mathbf{01}}\left({\mathit{\omega }}_n^{*}\right)-{\mathit{\theta }}_{\mathbf{02}}\left({\mathit{\omega }}_n^{*}\right))}{{\mathit{\omega }}_n^{*}{\mathit{ }\mathit{ }\mathit{ }\mathit{\theta }}_{\mathbf{02}}\left({\mathit{\omega }}_n^{*}\right)}}$$

(5)

with ${\mathit{\omega }}_n^{*}=n\pi$.