Natural-Born Intelligence as the Invocation of Emotion = Politics ^†

Abstract

This paper critiques the artificial intelligence (AI) framework as a self-referential system that relates parts to wholes without genuine creativity. Emotions—understood as forms of politics—emerge when top-down commands override local processes, a phenomenon absent in AI. Building on Bateson’s notion of the “play bite,” we propose Natural Born Intelligence (NBI): a system that simultaneously accepts and negates binary oppositions through positive and negative antinomies, thus opening itself to the “outside” beyond logical dualities. Found in brains, societies, and even chemical systems, NBI can be formalized through quantum logic and coherence across Hilbert spaces, offering a novel model of intelligence grounded in openness and emergence.

1. Introduction

Intelligence and life have usually been understood within the framework of artificial intelligence (AI). By this, I refer to a mode of thought in which understanding is achieved by relating two qualitatively different items. Russell and Norvig [1] define AI as “agents that receive percepts from the environment and perform actions.” This definition presupposes that perception transforms external objects into internal representations—an assumption that already relates inside and outside. Such presupposition defines the AI framework shared across major accounts [2,3].

A contemporary embodiment of this framework is the large language model (LLM) [4,5,6,7]. It continuously maps linguistic environments into high-dimensional vector spaces, treating language only insofar as it can be tokenized, embedded, and statistically correlated. For such systems, a poem, a scientific hypothesis, or a confession differ only in probability weighting among tokens. What cannot be encoded as a distribution of co-occurrence is effectively meaningless. This exemplifies how AI reduces thought to measurable regularities of language, closing itself to the creative emergence of meaning that arises beyond correlation [8,9,10].

In contrast, Natural Born Intelligence (NBI) is proposed as a framework of creative openness [11,12]. When two heterogeneous items confront each other, NBI does not resolve the contradiction but sustains it through two operations: positive antinomy (simultaneously accepting both) and negative antinomy (bleaching or nullifying both). By maintaining this fragile coexistence, NBI allows what is unforeseen—the “outside”—to enter the system. Emotions, in this sense, can emerge not from top-down design but as spontaneous formations of this openness.

In AI, emotions or feelings are often pre-programmed modules [13,14,15,16,17,18]; The essential question, then, is how such subsystems arise naturally. Bayesian inference and the free-energy principle [19,20] relate prior and posterior probabilities—still an act of relating. NBI begins when this very relation is both enacted and invalidated, making room for genuine creation.

2. Artificial Intelligence and Natural Born Intelligence

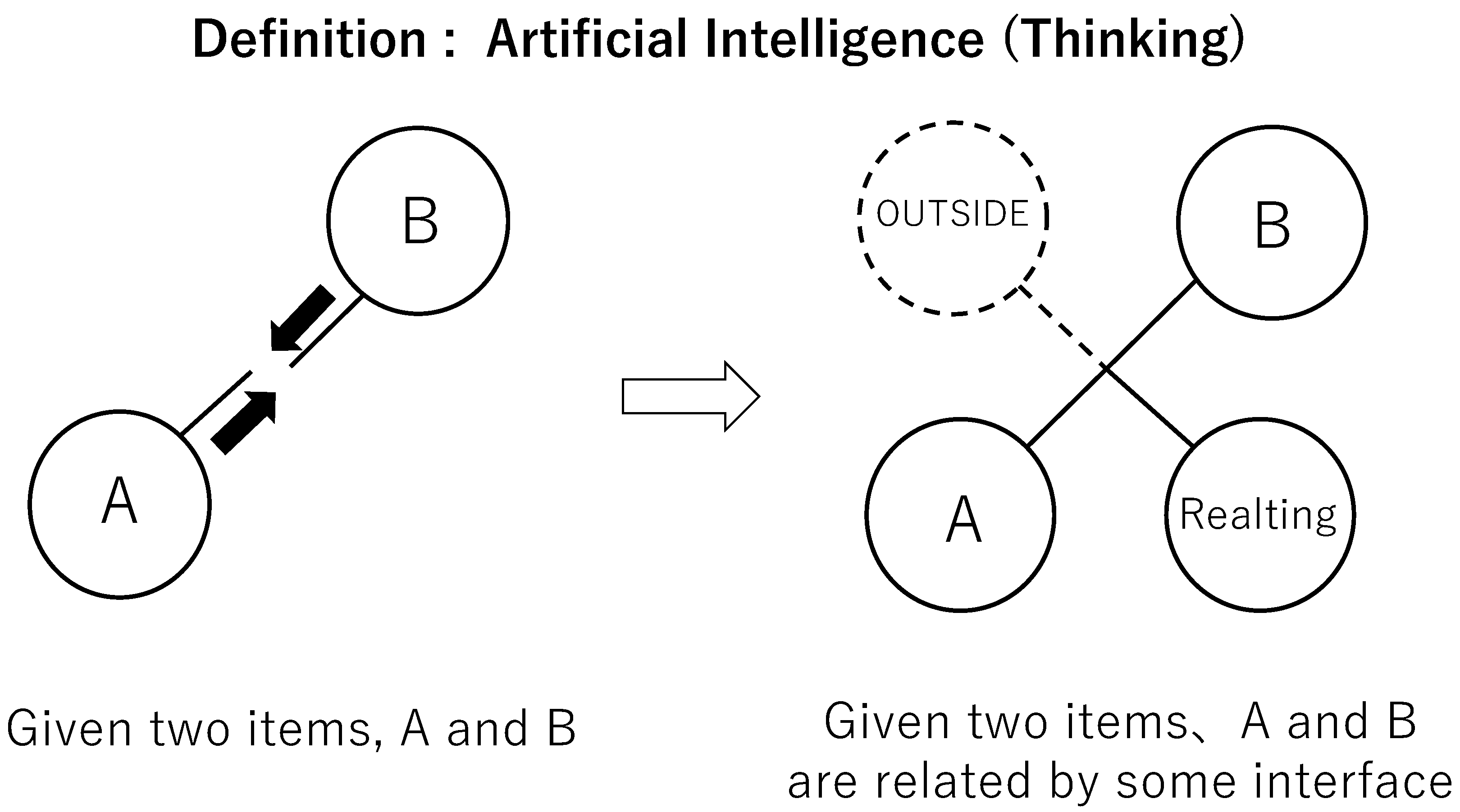
To clarify the concept of Natural Born Intelligence (NBI) [11], we must first examine the underlying mode of thought that constitutes artificial intelligence (AI)—what may be called AI thinking (Figure 1).

Let us assume that two qualitatively distinct items are given. When a system must make a decision, it ultimately confronts these two items, raising the question of how the final decision should be made. From this starting point, one typically chooses one side, reduces one to the other, or constructs a mediation that relates them. In other words, the very act of relating two heterogeneous items—A and B—is taken as equivalent to understanding. This is what I call AI thinking.

AI thinking represents a generalized extension of computation. In the early twentieth century, mathematicians such as Turing and von Neumann explored the nature of human thought and formalized it as computation through concepts such as the Turing machine, automata, and recursive functions [21]. These three forms of computation have since been proven equivalent. Recursive functions are constructed from the fundamental notions of the successor, projection, and composition functions, together with recursion and bounded operators. Each of these definitions is based on relating one thing to another, which exemplifies AI thinking.

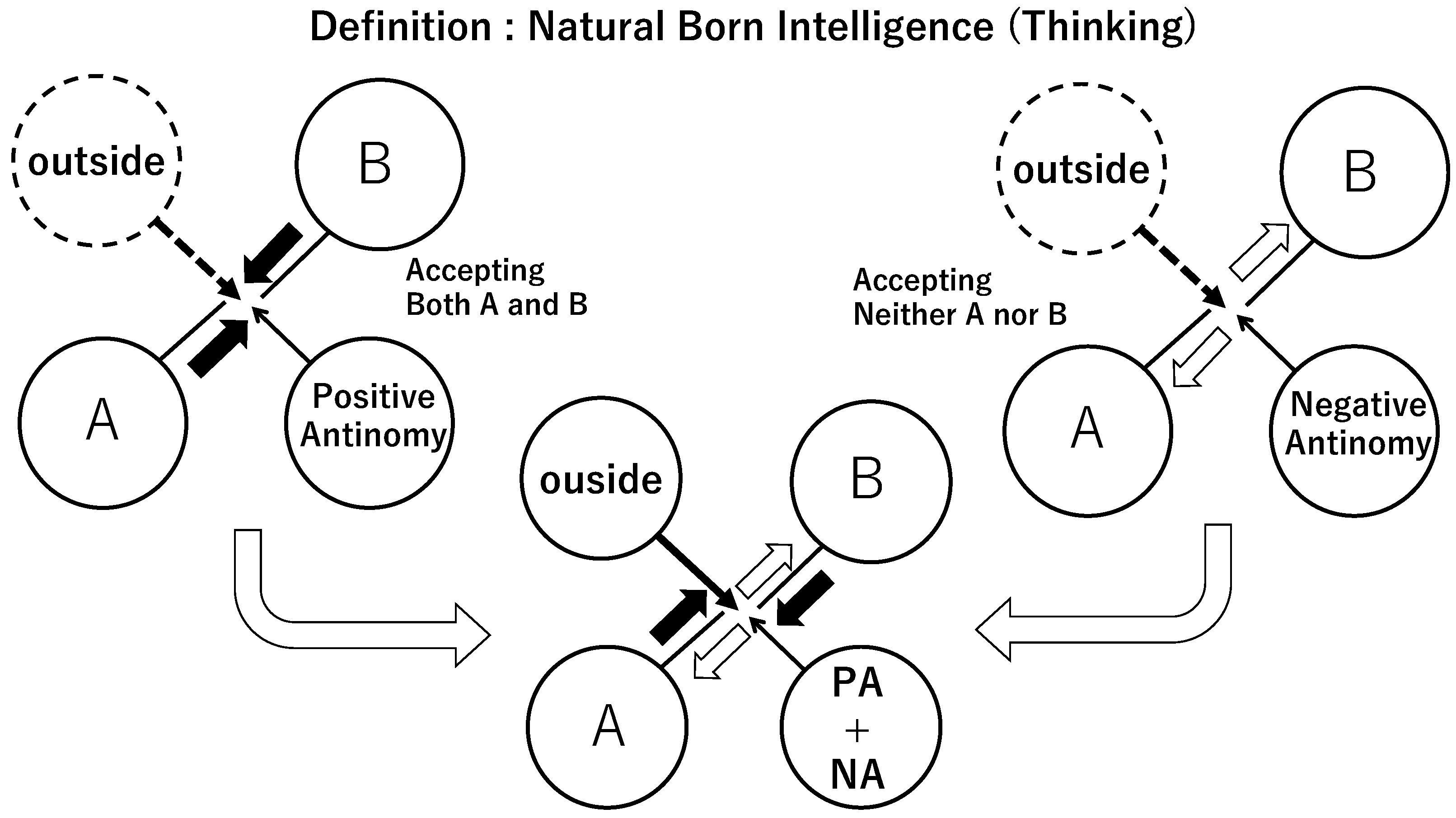
In contrast, Natural Born Intelligence does not regard the act of relating as understanding (Figure 2). Suppose that two distinct items, A and B, are given. As in AI, we may first attempt to relate them; this is what I call a positive antinomy. Despite its name, this is not a logical operation but an experiential one. In everyday cognition, we often hold two contradictory ideas simultaneously without resolving them. Next, we may invalidate the meanings of both A and B—regarding them as meaningless or “bleached.” This process I call a negative antinomy: rejecting both poles at once, destabilizing context, and dissolving meaning.

Natural Born Intelligence sustains both positive and negative antinomies. Each alone would approach contradiction and be difficult to maintain, but together they create a state of fragile stability. In this state, NBI does not act but waits—not as mere passivity, but as receptivity to something unforeseen that may come from the outside. NBI is therefore a thoroughly open system: one that amplifies, adjusts, and even employs fluctuations for its own stabilization.

A simple example may be found in childhood play. Many children have walked along a line drawn on the pavement, imagining it as the edge of a cliff. In the real world, the child is walking safely on flat ground, yet in imagination, they are on a precipice. Here, reality and imagination coexist and interact: a positive antinomy. At the same time, the child recognizes the absurdity of the game—bleaching both the reality of the pavement and the imagined cliff—thus forming a negative antinomy. These two antinomies coexist, producing the peculiar thrill of play and the feeling of “another world.” If reality and imagination were simply equated, the experience would be terrifying; if they were entirely separate, no play would occur. The child’s awareness of nonsense sustains both realities, making play—and creativity—possible.

Positive and negative antinomies are concepts defined at different levels. Their coexistence acquires meaning only when different levels are established. The first example of NBI can be found in unconventional computing [22] systems that employ biological or chemical substances—such as Physarum [23,24,25], proteinoid microspheres [26,27], or suspensions [28]—as computational media. These systems can perform logical computations in terms of bit sequences when dealing with input–output interactions with the user. At this computational level, the relationship between parts and wholes can be formally defined, enabling recursive representations and self-reference, thereby realizing a positive antinomy.

At the same time, the actual execution of computation corresponds to physical or chemical reaction processes, whose fine boundary conditions cannot be precisely controlled. The instability of these physical boundaries affects the computational operations themselves, potentially altering their behavior. In multilayered artificial neural networks, if they are implemented by unconventional computing, such fluctuations would influence the synaptic weights of each neuron. As long as the computation does not collapse and the underlying chemical or biological activity is maintained, these minute influences will remain unnoticed as “errors,” even though they silently transform the meaning of the computation. This instability of boundary conditions in material processes constitutes the negative antinomy.

Beyond computation as a physical process, NBI can also be instantiated in the coexistence of Bayesian and inverse Bayesian inference. Both in models of the brain and in artificial intelligence, learning constraints based on generalizing one’s own experience—such as the free-energy minimization principle—have dominated the field. This framework takes the form of minimizing the Kullback–Leibler divergence, and its goal is to realize Bayesian inference [20], which treats the conditional probability of a hypothesis given data, $P\left(h\right|d)$, as equivalent to the probability of the hypothesis itself, $P\left(h\right)$:

$$P\left(h\right)=P\left(h\right|d),$$

(1)

This equivalence implies a confusion between partial information, $P\left(h\right|d)$, and the overall probability, $P\left(h\right)$, representing a positive antinomy. In Bayesian inference, all hypotheses remain fixed; hence estimating their probabilities is meaningful and allows for rational decision-making. Inverse Bayesian inference [29], on the other hand, continuously monitors the frequency distribution of data from the external environment and reinterprets frequencies as probabilities. It then rewrites the likelihood of hypotheses by replacing it as follows for any data d:

$$P\left(d\right|h)=P(d)$$

(2)

In doing so, the hypothesis itself is altered, thereby invalidating the distinction between $P\left(h\right)$ and $P\left(h\right|d)$, and constructing a negative antinomy. Although other implementations of inverse Bayesian inference have been proposed, the coexistence of Bayesian and inverse Bayesian inference allows the coexistence of positive and negative antinomies within the NBI framework.

From a physical standpoint, what comes from “outside” the system may be described as noise. Natural Born Intelligence can thus be viewed as an open dynamical system that not only tolerates but actively employs noise, transforming fluctuations into coherence.

3. The Emergence of Emotion

Emotion functions as an efficient top-down command for decision-making. Neural networks, by contrast, operate bottom-up: stimuli propagate through successive neurons, each making local majority-rule decisions. Final judgments therefore require time to emerge at higher levels. Emotion, however, bypasses this slow accumulation, allowing an immediate leap from stimulus to action—for instance, from perception to fear and escape. How can such a top-down mechanism arise from bottom-up dynamics?

We approach this question through the framework of Natural Born Intelligence. Emotions and feelings can be understood as forms of politics: top-down commands that override lower-level processing. This “emotion = politics” formulation captures something absent in AI. In a neural network or an autonomous vehicle, responses are the result of hierarchical computation, not self-emergent authority.

Bateson’s notion of the “play bite” in wolves illustrates this. Neurons, like wolves, engage in local interactions that sometimes conflict. Yet the play bite introduces a meta-level rule that transcends individual behavior—a political command that suspends aggression and establishes cooperation. Bateson described this “gentle bite” as both a physical act and a metacommunicative sign [30,31]. AI can simulate the linkage between act and meaning, but it cannot generate new meaning from contradiction.

In natural systems, the play bite represents both a positive antinomy (“biting” and “not biting”) and a negative antinomy (the bleaching of aggression itself). This suspension of contradiction transforms hostility into communication—a model of emotional emergence. Bateson’s “double bind” captures the positive antinomy but misses the deeper negative one, where antagonism itself is negated, allowing a tacit contract—“not attacking = not being attacked”—to arise. This negative antinomy makes communicative play possible.

At the neuronal level, excitation corresponds to positive antinomy, while inhibition and refractory dynamics realize negative antinomy. When excitation alone dominates, activity reaches a deadlock; emotion breaks through as a political, top-down force that reorganizes the collective. Fear, for example, interrupts deliberative processing and enforces rapid unified action.

In neuroscience and AI, the free-energy principle embodies Bayesian inference, relating priors and posteriors as a positive antinomy [19,20]. Yet this relation alone generalizes experience without generating novelty. To move beyond experience, the system must enact and invalidate the relation simultaneously—a negative antinomy. Inverse Bayesian inference [29,32] formalizes this, allowing for the spontaneous emergence of phenomena such as play and emotion-as-politics.

Natural Born Intelligence is not confined to biological brains. Even chemical systems exhibit similar dynamics, harnessing fluctuations beyond the scope of quantum logic. A positive antinomy between distinct Hilbert spaces corresponds to entanglement, while admitting cross-space fluctuations represents a negative antinomy. The coexistence of both leads to coherence beyond quantum logic, grounding the emergence of creative phenomena.

4. Quantum Logic and Open Quantum

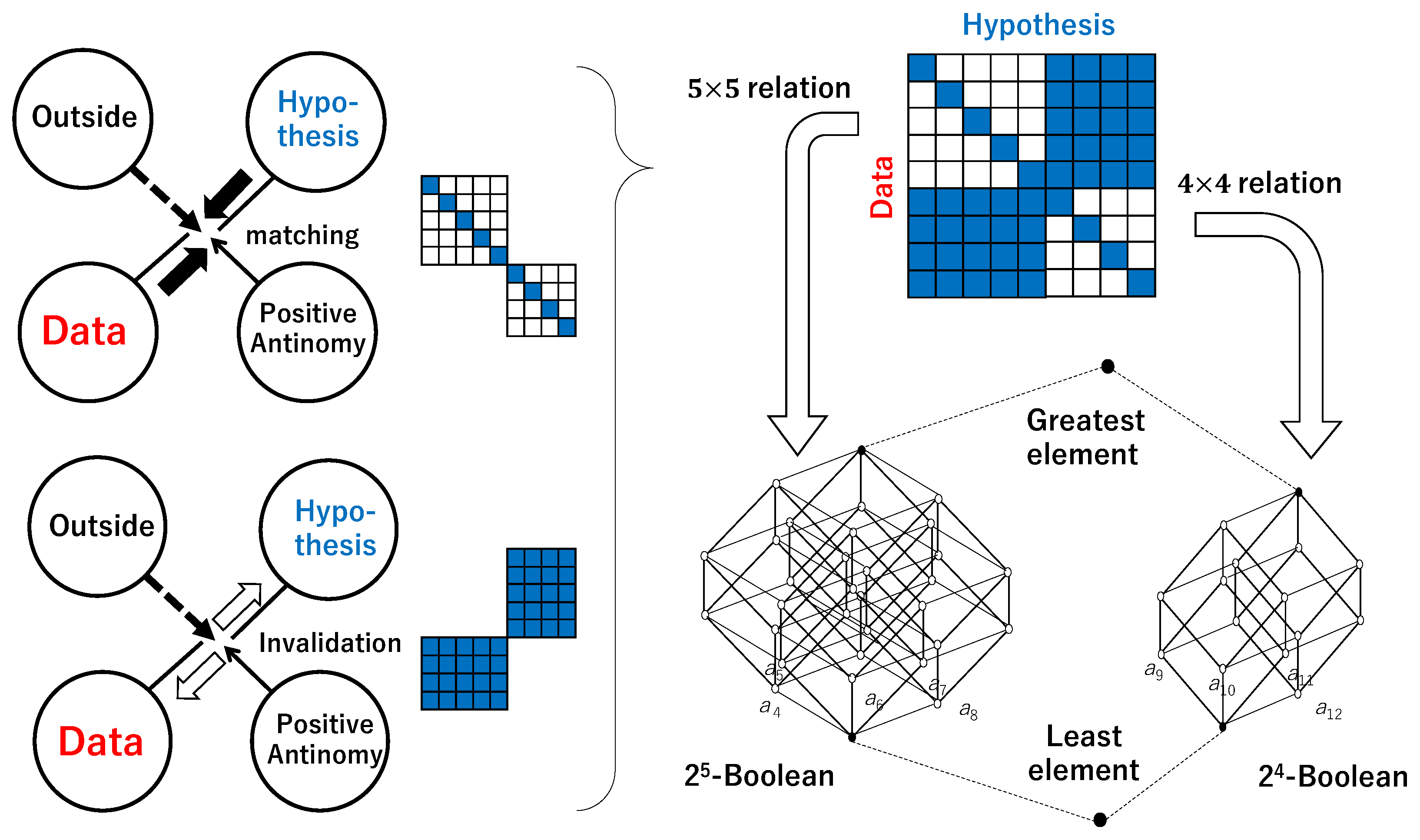
Natural Born Intelligence—whether concerning reality and virtuality or priors and posteriors—can be formalized through rough set approximations [33] to quantum logic, represented by a non-distributive orthomodular lattice [12,34]. Figure 3 illustrates how such quantum logic emerges.

In Bayesian inference, priors and posteriors are connected through the joint probability of data and hypothesis, which can be represented as a binary relation between data set and hypothesis set—a subset of their Cartesian product. Below a threshold probability, we regard no relation as existing; above it, a relation is defined.

Within this binary relation, the positive antinomy between data and hypothesis appears as a matching—a one-to-one correspondence established independently across multiple contexts. In Figure 3, this is shown as diagonal sub-relations across contexts. The negative antinomy, conversely, manifests as noise: nonzero probabilities off the diagonal, producing a dense spread of off-diagonal relations. Superimposing both yields the configuration at the right of Figure 3: two diagonal sub-relations overlaid with pervasive noise.

From this structure, we define upper and lower approximations of rough sets [32,35]. For any $X\subseteq D$ and any $Y\subseteq H$,

$$K^{\ast }\left(X\right)=\{h\in H|\exists d\in X((h,d)\in R)\}$$

(3)

$$S_{\ast }\left(Y\right)=\{d\in D|\forall h\in H((h,d)\in R)\Rightarrow h\in Y\}$$

(4)

Collecting the fixed points of the composition of these approximations—known as the quasi-closure operation—produces a structure that has been proven to form a lattice, that is, a partially ordered set closed under join and meet [35,36], that is,

$$L=\{X\subseteq D|S_{\ast }\left(K^{\ast }\left(X\right)\right)=X\}.$$

(5)

When the relation is purely diagonal, the resulting lattice is Boolean—fully compatible with set theory and classical logic. However, when multiple diagonal sub-relations coexist and all off-diagonal regions are filled, the resulting structure comprises overlapping Boolean algebras sharing both maximal and minimal elements. This overlapping generates quantum logic [37]: a non-distributive orthomodular lattice [34,38,39].

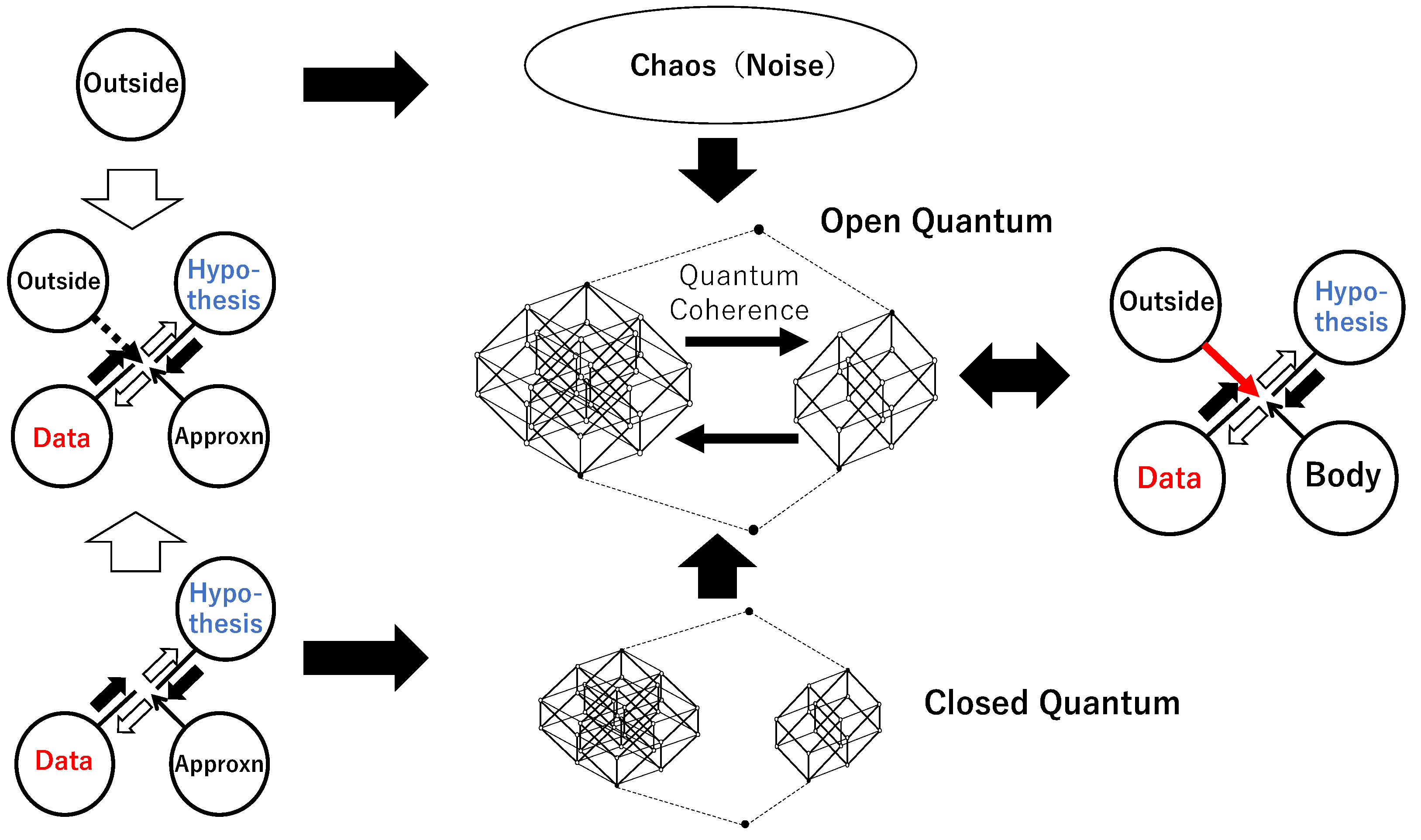
Boolean sub-algebras correspond to Hilbert spaces; their shared elements represent quantum entanglement. Natural born intelligence is therefore not limited to neural or social systems [12]—it appears in chemical reaction networks and other physical systems [37,40] where fluctuations operate through and beyond quantum logic. The positive antinomy between distinct Hilbert spaces corresponds to entanglement, and the negative one to fluctuations traversing those spaces. When both coexist, quantum logic breaks down, yet coherence of a higher order emerges—resonances across distinct Hilbert spaces. This cross-space coherence represents the outside that NBI invites: a meta-logical openness where emotion and creativity can arise.

When the coexistence of positive and negative antinomies in cognition or chemical reactions is represented as a binary relation, the two are differentiated within the table of that relation. The positive antinomy corresponds to a sub-relation that includes only the diagonal elements—relations that hold solely along the diagonal—whereas the negative antinomy corresponds to a block-like sub-relation composed entirely of relations. When the stability of such binary relations is analyzed in terms of lattices of rough sets, it becomes evident that both cognitive processes and chemical reactions exhibit an informationally quantum composite system that is independent of any physical substrate. This informationally quantum composite system amplifies fluctuations and induces intense information flow among subsystems corresponding to different Hilbert spaces, thereby endowing the system with a dynamic and nonlocal order structure. This constitutes what may be called informational quantum coherence (Figure 4).

5. Discussion

Although the present study focuses on the theoretical articulation of Natural Born Intelligence (NBI), its principles have been partially examined in empirical contexts, such as proteinoid microsphere spiking [37] and cognitive phenomena [12]. These systems demonstrate how coherence can emerge through structural transformation under environmental perturbations, consistent with the NBI view that intelligence originates from openness and contradiction rather than optimization. Future work will formalize these processes via simulation-based or quantitative modeling of such open dynamics.

Our proposed NBI (Natural Born Intelligence) is based on the principle that it is self-referential (positive antinomy) and simultaneously decolorizes the meaning of what constitutes self-reference (negative antinomy). We argue that NBI is a mode of existence as an open quantum system in the sense of regulating fluctuations.

Does this claim contradict to Khrennikov and Schumanns’ claim [41] that quantum phenomena are self-referential and performative? They emphasize self-referential form and leave performativity to the observer’s choice. However, it is precisely on the extension of the ambiguity of both self-reference and performativity that the coexistence of our claimed positive antinomy and negative antinomy exists, and the claim is not contradictory at all, but rather highly consistent.

How can we use self-reference positively, not as a contradiction or something negative? This is where the meaning of performativity lies. The statement “This statement is false” is self-referential and contradictory, which can be determined by mechanical operation. Logically, it is a contradiction, but using it positively while ignoring the contradiction is possible through performativity. For example, it is possible to find literary interest in “This statement is false” and use it as a monologue of the protagonist, or to use “This statement is false” as a secret code among friends in everyday life. That is an example of using this sentence regardless of the contradiction. It can be said that this is a “meaning-making process” brought from outside the logic that determines “This statement is false” as a contradiction. “Meaning-making process” is something that gives meaning to words and expressions, but it cannot be predetermined and appears as a result. In other words, performativity can be rephrased as “meaning-making process”. Because semantic function is located outside of what is mathematically and logically defined, Khrennikov and Schumann position it as the observer’s choice [41]. However, in this case, the quantum phenomenon and the observer are completely separated. This would be the same as separating semantic function from “This statement is false” within logic. It would be the same as the argument that no matter how advanced artificial intelligence becomes, ultimately it is humans who find value in it. No, it is not the same. Performativity is emphasized to the extent that structural self-reference and performativity are juxtaposed [41].

We are not completely separating the quantum phenomenon and the observer, or logic and “meaning-making process”, but rather weakening that separation and proposing NBI as something that summoning “meaning-making process”. Self-reference constitutes a positive antinomy in the sense that it accepts both heterogeneous items, the part and the whole. The negative antinomy that decolorizes it attempts to summon the use of self-reference independently of the logically defined “contradiction”. If it is ultimately successful, it will be called “performative”. Natural born intelligence is necessarily performative, and it does not claim that any semantic function can be predetermined. If so, “ meaning-making process” would also be implemented as a mechanical, logical operation. It is a gamble on success, but it is a mechanism outside of the mechanical, logical, and mathematical system that is better than trial and error. In that sense, the positive/negative antinomy of NBI can be considered an extension of self-reference and performative quantum phenomena or concepts.

Unlike contemporary computational theories such as predictive processing [20,42], hierarchical reinforcement learning [43,44], meta-control [45] and expected value of control theory [46] which assume a hierarchical and goal-oriented structure of cognition, the Natural Born Intelligence (NBI) framework emphasizes an open system that transforms itself in response to contradictions and perturbations. Rather than minimizing prediction error or maximizing reward, NBI integrates environmental noise as a source of structural renewal, thereby redefining the boundary between agent and environment.

6. Conclusions

This study contrasted the framework of artificial intelligence (AI) with that of Natural Born Intelligence (NBI). AI presupposes the relation of heterogeneous items and thus remains confined within experience—exemplified by Bayesian inference and the free-energy principle. NBI, by contrast, sustains both positive antinomy (accepting contradictions) and negative antinomy (bleaching meanings), producing a delicate openness to the unforeseen. Through this openness, new subsystems—such as emotions—can emerge. The wolf’s play bite exemplifies how antagonism can be both affirmed and negated, transforming aggression into communication: emotion = politics. At the neuronal level, excitation and inhibition generate deadlocks that emotion overcomes through top-down integration. Formalized via rough set approximations to quantum logic, NBI mobilizes fluctuations that transcend logical closure. It thus reveals intelligence not as computation or self-reference, but as receptivity to the outside: a principle of creation shared by neural, social, and even chemical systems.

This study redefines intelligence as an open process in contrast to the closed framework of AI. By formalizing the coexistence of positive and negative antinomies as the basis of Natural Born Intelligence (NBI), we show that creativity and emotion emerge through receptivity to the unforeseen rather than internal optimization. Future work should connect NBI with contemporary AI models, including large language systems, to explore how openness may enable genuine meaning formation. Experimental studies using unconventional computing media—such as chemical or biological systems—may further reveal how fluctuation and noise function as sources of intelligence and creation.