Nonlinear Evolution Equations of the Soliton Type: Old and New Results †
Abstract
1. Introduction
2. Preliminary Notions and Bäcklund Transformations
- If admits a Recursion Operator , then we can write
- the Recursion Operator is such that
- 1.
- Φ maps symmetries into symmetries (A map is said to be an infinitesimal symmetry generator (for short symmetry) if it leaves the evolution equation invariant under the infinitesimal transformation .
- 2.
- Thus, if u and σ are solutions, in turn, of and , then is also a solution of the latter. That is
- 3.
- Φ is hereditary, i.e., satisfies the condition
- Then, is a recursion operator for the hierarchy .
- The property to admit a Recursion operator is preserved under Bäcklund Transformations.
3. Extension to Hierachies
4. Operator Bäcklund Charts
4.1. Heat–Burgers Operator Bäcklund Charts
4.2. KdV–mKdV Operator Bäcklund Charts
5. Third-Order Bäcklund Chart: An Extension
6. Fifth-Order Bäcklund Chart: An Extension
7. Remarks, Perspectives, and Open Problems
7.1. Remarks and Further Obtained Results
- New Solutions
- -
- Abelian case: One very important consequence of the constructed Bäcklund Charts is that new solutions of nonlinear evolution equations can be constructed from known solutions of other equations in the same Chart. This was the case in [79], where solutions admitted by the Harry Dym equation were obtained from solutions of the KdV equation.
- -
- Non-Abelian case: Even more interesting is the case of Bäcklund Chart operators, in which new solutions can be obtained from known ones. Solutions of non-commutative equations are of great interest [69,80], such as in the case of a solution formula for the non-Abelian mKdV equation: we constructed solutions of the non-Abelian mKdV equation from solutions admitted by the non-Abelian KdV equation, obtained by Goncharenko [81]. In particular, matrix solutions admitted by the non-Abelian mKdV equation were obtained in [82] and references therein; a different approach to the matrix mKdV solution was given in [83]. Other approaches to non-Abelian cases are also interesting [21,63,84].
- New Invariances and Auto Bäcklund Transformations(Abelian and non-Abelian cases)
- -
- In both cases, via the constructed Bäcklund Charts, new invariance exhibited by the involved equations can be obtained, or well-known ones can be recovered. Results in this line are in [56,57] in cases of 5th-order nonlinear evolution equations, while in [74,85,86], invariances exhibited by 3rd-order nonlinear evolution equations connected with the KdV equation, via the Bäcklund Chart in Figure 1, were obtained. Furthermore, auto Bäcklund transformations admitted by the Harry Dym equation were obtained [74,85]. Remarkably, also in the non-Abelian case, interesting properties of the nonlinear evolution equations which appear in the Bäcklund Chart [68,69,87,88], follow from the chart itself; such as, e.g., to admit a recursion operator. A comparison between the Abelian and non-Abelian Bäcklund Charts concerning 3rd-order nonlinear evolution equations is given in [89]. Indeed, as pointed out therein, a richer structure [88], based also on results in [90], was revealed in the non-commutative case. In addition, further equations appear to be connected in the Bäcklund Chart previously obtained.
7.2. Perspectives and Open Problems
- Extensions from Abelian to non-Abelian in the case of 5th-order nonlinear evolution equations, which appear in the Bäcklund Chart in [75], are under investigation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kasman, A. Glimpses of Soliton Theory: The Algebra and Geometry of Nonlinear PDEs, 2nd ed.; College of Charleston: Charleston, SC, USA; American Mathematical Society: Providence, RI, USA, 2023; p. xvi+347. ISBN 9781470472627/9781470473105. [Google Scholar]
- Drazin, P.G.; Johnson, R.S. Solitons: An Introduction; Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 1989; p. xii+226. ISBN 0-521-33389-X. [Google Scholar]
- Singh, P.; Senthilnathan, K. Evolution of a solitary wave: Optical soliton, soliton molecule and soliton crystal. Discov. Appl. Sci. 2024, 6, 464. [Google Scholar] [CrossRef]
- Alonzo, M.; Moscatelli, D.; Bastiani, L.; Belardini, A.; Soci, C.; Fazio, E. All-Optical Reinforcement Learning in Solitonic X-Junctions. Sci. Rep. 2018, 8, 5716. [Google Scholar] [CrossRef]
- Fazio, E.; Alonzo, M.; Belardini, A. Addressable Refraction and Curved Soliton Waveguides Using Electric Interfaces. Appl. Sci. 2019, 9, 347. [Google Scholar] [CrossRef]
- Kivshar, Y.S. Dark-soliton dynamics and shock waves induced by the stimulated Raman effect in optical fibers. Phys. Rev. A 1990, 42, 1757. [Google Scholar] [CrossRef]
- Platschorre, A. A mass for the dual axion. J. High Energy Phys. 2024, 2024, 253. [Google Scholar] [CrossRef]
- Nakamura, Y.; Tsukabayashi, I. Observation of modified Korteweg-de Vries solitons in a multicomponent plasma with negative ions. Phys. Rev. Lett. 1984, 52, 2356. [Google Scholar] [CrossRef]
- Lautrup, B.; Appali, R.; Jackson, A.D.; Heimburg, T. The stability of solitons in biomembranes and nerves. Eur. Phys. J. E 2011, 34, 57. [Google Scholar] [CrossRef]
- Veenstra, J.; Gamayun, O.; Guo, X.; Sarvi, A.; Meinersen, C.V.; Coulais, C. Non-reciprocal topological solitons in active metamaterials. Nature 2024, 627, 528–533. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; He, J.S.; Pelloni, B. Preface: Integrable systems and their applications, celebrating the 70th birthday of Athanassios S. Fokas. Stud. Appl. Math. 2024, 153, e12707. [Google Scholar] [CrossRef]
- Olver, P.J. Evolution equations possessing infinitely many symmetries. J. Math. Phys. 1977, 18, 1212–1215. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Groups to Differential Equations; GTM vol. 107; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Ovsjannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA; London, UK, 1982. [Google Scholar]
- Olver, P.J.; Wang, J.P. Classification of Integrable One-Component Systems on Associative Algebras. Proc. Lond. Math. Soc. 2000, 81, 566–586. [Google Scholar] [CrossRef]
- Hirota, R. Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 1971, 17, 1192–1194. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Matveev, V.B.; Salle, M.A. Darboux Transformation and Solitons; Springer: Berlin, Germany, 1991. [Google Scholar]
- Sakhnovich, A.L.; Sakhnovich, L.A.; Roitberg, I.Y. Inverse Problems and Nonlinear Evolution Equations. Solutions, Darboux Matrices and Weyl-Titchmarsh Functions. In Studies in Mathematics; De Gruyter: Berlin, Germany, 2013; Volume 47. [Google Scholar]
- Calogero, F.; Degasperis, A. A modified modified Korteweg-de Vries equation. Inverse Probl. 1985, 1, 57–66. [Google Scholar] [CrossRef]
- Olver, P.J.; Sokolov, V.V. Integrable evolution equations on nonassociative algebras. Comm. Math. Phys. 1998, 193, 245–268. [Google Scholar] [CrossRef]
- Wang, J.P. A List of 1 + 1 Dimensional Integrable Equations and Their Properties. J. Nonlinear Math. Phys. 2002, 9, 213–233. [Google Scholar] [CrossRef]
- Mikhailov, A.V.; Shabat, A.B.; Yamilov, R.I. The symmetry approach to the classification of non-linear equations. Complete lists of integrable systems. Russ. Math. Surv. 1987, 42, 1. [Google Scholar] [CrossRef]
- Mikhailov, A.V.; Novikov, V.S.; Wang, J.P. On Classification of Integrable Nonevolutionary Equations. Stud. Appl. Math. 2007, 118, 419–457. [Google Scholar] [CrossRef]
- Basarab-Horwath, P.; Güngör, F. Linearizability for third order evolution equations. J. Math. Phys. 2017, 58, 081507. [Google Scholar] [CrossRef]
- Ziegler, M.; Fuchssteiner, B. Nonlinear reformulation of Heisenberg’s dynamics. Int. J. Theor. Phys. 2005, 44, 693–717. [Google Scholar] [CrossRef]
- Fokas, A.S. A Symmetry Approach to Exactly Solvable Evolution Equations. J. Math. Phys. 1980, 21, 1318–1325. [Google Scholar] [CrossRef]
- Fokas, A.S. Symmetries and Integrability. Stud. Appl. Math. 1987, 77, 253–299. [Google Scholar] [CrossRef]
- Levi, D. Toward a unification of the various techniques used to integrate nonlinear partial differential equations: Bäcklund and Darboux transformations vs. dressing method. Rep. Math. Phys. 1986, 23, 41–56. [Google Scholar] [CrossRef]
- Grimshaw, R.H.J.; Liu, Z. Nonlinear periodic and solitary water waves on currents in shallow water. Stud. Appl. Math. 2017, 139, 60–77. [Google Scholar] [CrossRef]
- Kruskal, M.D. Nonlinear Wave Equations. In Dynamical Systems, Theory and Applications; Moser, J., Ed.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1975; Volume 38, pp. 310–348. [Google Scholar]
- Zakharov, V.E.; Shabat, A. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62–69. [Google Scholar]
- Bäcklund, A.V. Über Flächentransformationen. Math. Ann. 1876, 9, 279–320. [Google Scholar]
- Bäcklund, A.V. Zur Theorie der Flächentransformationen. Math. Ann. 1881, 19, 387–420. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Calogero, F.; Degasperis, A. Spectral Transform and Solitons I; North Holland: Amsterdam, The Netherlands, 1980; Volume 13. [Google Scholar]
- Eckhaus, W.; Harten, A.V. The Inverse Scattering Transformation and The Theory of Solitons. North Holland Math Studies; North Holland: Amsterdam, The Netherlands, 1981; Volume 50. [Google Scholar]
- Rogers, C.; Shadwick, W.F. Bäcklund Transformations and Their Applications; Mathematics in Science and Engineering; Academic Press: New York, NY, USA; London, UK, 1982; Volume 161. [Google Scholar]
- Rogers, C.; Ames, W.F. Nonlinear Boundary Value Problems in Science and Engineering; Academic Press: Boston, MA, USA, 1989. [Google Scholar]
- Rogers, C.; Schief, W.K. Bäcklund and Darboux Transformations: Geometry and Modern Applications in Soliton Theory; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Gu, C.; Hu, H.; Zhou, Z. Darboux Transformations in Integrable Systems; Springer: Dordrecht, The Netherlands, 2005; ISBN 1-4020-3087-8. [Google Scholar]
- Levi, D. Bäcklund Transformations. In Encyclopedia of Mathematical Physics; Françoise, J.-P., Naber, G.L., Tsun, T.S., Eds.; Academic Press: Cambridge, MA, USA, 2006; pp. 241–247. ISBN 9780125126663. [Google Scholar]
- Fuchssteiner, B. Application of hereditary symmetries to nonlinear evolution equations. Nonlin. Anal. Theory Meth. Appl. 1979, 3, 849–862. [Google Scholar] [CrossRef]
- Gelfand, I.M.; Dorfman, I.Y. Hamiltonian operators and algebraic structures related to them. Func. Anal. Appl. 1979, 13, 13–30. [Google Scholar]
- Magri, F. A Simple Model of the Integrable Hamiltonian Equation. J. Math. Phys. 1978, 19, 1156–1162. [Google Scholar] [CrossRef]
- Fokas, A.S.; Fuchssteiner, B. On the Structure of Symplectic Operators and Hereditary Symmetries. Lett. Nuovo Cimento 1980, 28, 299–307. [Google Scholar] [CrossRef]
- Fokas, A.S.; Fuchssteiner, B. Bäcklund transformation for hereditary symmetries. Nonlin. Anal. Theory Methods Appl. 1981, 5, 423–432. [Google Scholar] [CrossRef]
- Fuchssteiner, B. The Lie algebra structure of Degenerate Hamiltonian and Bi-Hamiltonian systems. Prog. Theor. Phys. 1982, 68, 1082–1104. [Google Scholar] [CrossRef]
- Gürses, M.; Karasu, A.; Sokolov, V.V. On construction of recursion operators from Lax representation. J. Math. Phys. 1999, 40, 6473–6490. [Google Scholar] [CrossRef]
- Hereman, W.; Colagrosso, M. Symbolic computation of recursion operators for nonlinear partial differential equations. Math. Comput. Simul. 1997, 43, 13–27. [Google Scholar] [CrossRef]
- Fuchssteiner, B.; Oevel, W.; Wiwianka, W. Computer-algebra methods for investigating hereditary operators of higher order soliton equations. Comput. Phys. Commun. 1987, 44, 47–55. [Google Scholar] [CrossRef]
- Cole, J.D. On a quasilinear parabolic equation occurring in aerodynamics. Quart. Appl. Math. 1951, 92, 25–236. [Google Scholar]
- Hopf, E. The partial differential equation ut + uux = μuxx. Comm. Pure Appl. Math. 1950, 3, 201–230. [Google Scholar] [CrossRef]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteweg-de Vries equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. The Inverse Scattering Transform-Fourier Analysis for Nonlinear Problems. Stud. Appl. Math. 1974, 53, 249–315. [Google Scholar] [CrossRef]
- Carillo, S.; Fuchssteiner, B. The abundant symmetry structure of non linear equations obtained by reciprocal links. J. Math. Phys. 1989, 30, 1606–1613. [Google Scholar] [CrossRef]
- Rogers, C.; Carillo, S. On reciprocal properties of the Caudrey-Dodd-Gibbon and Kaup-Kupershmidt hierarchies. Phys. Scr. 1987, 36, 865–869. [Google Scholar] [CrossRef]
- Carillo, S.; Schiebold, C. On the recursion operator for the non-commutative Burgers hierarchy. J. Nonlin. Math. Phys. 2012, 19, 1250003. [Google Scholar]
- Carillo, S.; Lo Schiavo, M.; Schiebold, C. Recursion Operators admitted by non-Abelian Burgers equations: Some Remarks. Math. Comput. Simul. 2018, 147, 40–51. [Google Scholar] [CrossRef]
- Levi, D.; Ragnisco, O.; Bruschi, M. Continuous and discrete matrix Burgers’ hierarchies. Il Nuovo C. B 1983, 74, 33–51. [Google Scholar] [CrossRef]
- Gürses, M.; Karasu, A.; Turhan, R. On non-commutative integrable Burgers equations. J. Nonlinear Math. Phys. 2010, 17, 1–6. [Google Scholar] [CrossRef]
- Kupershmidt, B.A. On a group of automorphisms of the noncommutative Burgers hierarchy. J. Nonlinear Math. Phys. 2005, 12, 539–549. [Google Scholar] [CrossRef]
- Hamanaka, M.; Toda, K. Noncommutative Burgers equation. J. Phys. A Math. Gen. 2003, 36, 11981. [Google Scholar] [CrossRef]
- Aden, H.; Carl, B. On realizations of solutions of the KdV equation by determinants on operator ideals. J. Math. Phys. 1996, 37, 1833–1857. [Google Scholar] [CrossRef]
- Wang, N.; Wadati, M. A new approach to noncommutative soliton equations. J. Phys. Soc. Jpn. 2003, 72, 3055. [Google Scholar] [CrossRef]
- Treves, F. Noncommutative KdV hierarchy. Rev. Math. Phys. 2007, 19, 677. [Google Scholar] [CrossRef]
- Nimmo, J.J. On a nonAbelian Hirota-Miwa equation. J. Phys. A 2006, 39, 5053. [Google Scholar] [CrossRef]
- Carillo, S.; Schiebold, C. Noncommutative Korteweg-de Vries and modified Korteweg-de Vries hierarchies via recursion methods. J. Math. Phys. 2009, 50, 073510. [Google Scholar] [CrossRef]
- Carillo, S.; Schiebold, C. Matrix Korteweg-de Vries and modified Korteweg-de Vries hierarchies: Noncommutative soliton solutions. J. Math. Phys. 2011, 52, 053507. [Google Scholar] [CrossRef]
- Bhatia, R.; Rosenthal, P. How and why to solve the operator equation AX − XB = Y. Bull. Lond. Math. Soc. 1997, 29, 1–21. [Google Scholar] [CrossRef]
- Calogero, F.; Degasperis, A. Reduction Technique for Matrix Nonlinear Evolution Equations solvable by the Spectral Transform. J. Math. Phys. 1981, 22, 23–31. [Google Scholar] [CrossRef]
- Carillo, S. KdV-type equations linked via Bäcklund transformations: Remarks and perspectives. Appl. Numer. Math. 2019, 141, 81–90. [Google Scholar] [CrossRef]
- Konopelchenko, B.G. Soliton eigenfunction equations: The IST integrability and some properties. Rev. Math. Phys. 1990, 2, 399–440. [Google Scholar] [CrossRef]
- Fuchssteiner, B.; Carillo, S. Soliton structure versus singularity analysis: Third order completely integrable nonlinear equations in 1+1 dimensions. Physica 1989, 154, 467–510. [Google Scholar] [CrossRef]
- Carillo, S.; Schiebold, C.; Zullo, F. A Fifth Order Nonlinear Evolution Equation: Connection to Caudrey-Dodd-Gibbon-Sawata-Kotera Equation; Dipartimento di “Scienze di Base e Applicate per lIngegneria”, Sapienza University of Rome: Rome, Italy, 2025; preprint. [Google Scholar]
- Caudrey, P.J.; Dodd, R.K.; Gibbon, J.D. A new hierarchy of Korteweg-de Vries equations. Proc. R. Soc. Lond. Ser. A 1976, 351, 407. [Google Scholar]
- Kawamoto, S. An exact Transformation from the Harry Dym Equation to the modified KdV Equation. J. Phys. Soc. Japan 1985, 54, 2055–2056. [Google Scholar] [CrossRef]
- Sawada, A.K.; Kotera, A.T. A method for finding N-soliton solutions of the KdV and KdV-like equations. J. Prog. Theor. Phys. 1974, 51, 1355–1367. [Google Scholar] [CrossRef]
- Fuchssteiner, B.; Schulze, T.; Carillo, S. Explicit solutions for the Harry Dym equation. J. Phys. A 1992, 25, 223–230. [Google Scholar] [CrossRef]
- Carl, B.; Schiebold, C. Nonlinear equations in soliton physics and operator ideals. Nonlinearity 1999, 12, 333–364. [Google Scholar] [CrossRef]
- Goncharenko, V.M. Multisoliton solutions of the matrix KdV equation. Theor. Math. Phys. 2001, 126, 81–91. [Google Scholar] [CrossRef]
- Carillo, S.; Lo Schiavo, M.; Schiebold, C. N-soliton matrix mKdV solutions: Some Special Solutions Revisited. Stud. Appl. Math. 2025, 154, e70061. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.; Liang, J.; Wang, R. The N-soliton solutions for the matrix modified Korteweg-de Vries equation via the Riemann-Hilbert approach. Eur. Phys. J. Plus 2020, 135, 574–582. [Google Scholar] [CrossRef]
- Hamanaka, M. Noncommutative solitons and quasideterminants. Phys. Scr. 2014, 89, 038006. [Google Scholar] [CrossRef]
- Rogers, C.; Nucci, M.C. On reciprocal Bäcklund transformations and the Korteweg-de Vries hierarchy. Phys. Scr. 1986, 33, 289–292. [Google Scholar] [CrossRef]
- Guo, B.-Y.; Rogers, C. On the Harry Dym equation and its solution. Sci. China Ser. A Math. Phys. Astron. Technol. Sci. 1989, 32, 283. [Google Scholar]
- Carillo, S.; Lo Schiavo, M.; Schiebold, C. Bäcklund Transformations and Non Abelian Nonlinear Evolution Equations: A novel Bäcklund chart. SIGMA 2016, 12, 087. [Google Scholar] [CrossRef]
- Carillo, S.; Lo Schiavo, M.; Porten, E.; Schiebold, C. A novel noncommutative KdV-type equation, its recursion operator, and solitons. J. Math. Phys. 2018, 59, 3053–3060. [Google Scholar] [CrossRef]
- Carillo, S.; Lo Schiavo, M.; Schiebold, C. Abelian versus non-Abelian Bäcklund charts: Some remarks. Evol. Equ. Control Theory 2019, 8, 43–55. [Google Scholar] [CrossRef]
- Athorne, C.; Fordy, A. Generalised KdV and MKdV equations associated with sym- metric spaces. J. Phys. A Math. Gen. 1987, 20, 1377–1386. [Google Scholar] [CrossRef]
- Fordy, P.A.; Gibbons, J. Some remarkable nonlinear Transformations. Phys. Lett. A 1980, 75, 325. [Google Scholar] [CrossRef]
- Fuchssteiner, B.; Carillo, S. The Action-Angle Transformation for Soliton Equations. Phys. A 1990, 166, 651–676. [Google Scholar] [CrossRef]
- Fuchssteiner, B. The Lie algebra structure of Nonlinear Evolution Equations admitting Infinite Dimensional Abelian Symmetry Groups. Prog. Theor. Phys. 1981, 65, 861–876. [Google Scholar] [CrossRef]
- Fuchssteiner, B. Linear aspects in the theory of solitons and nonlinear integrable equations. J. Phys. Soc. Japan 1991, 60, 1473–1496. [Google Scholar] [CrossRef]
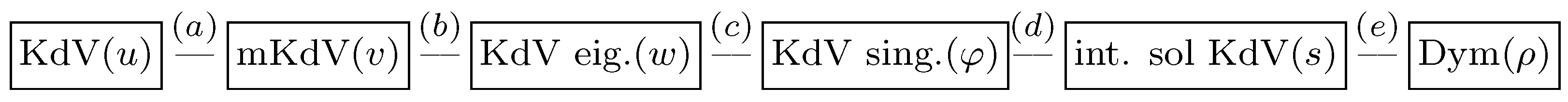
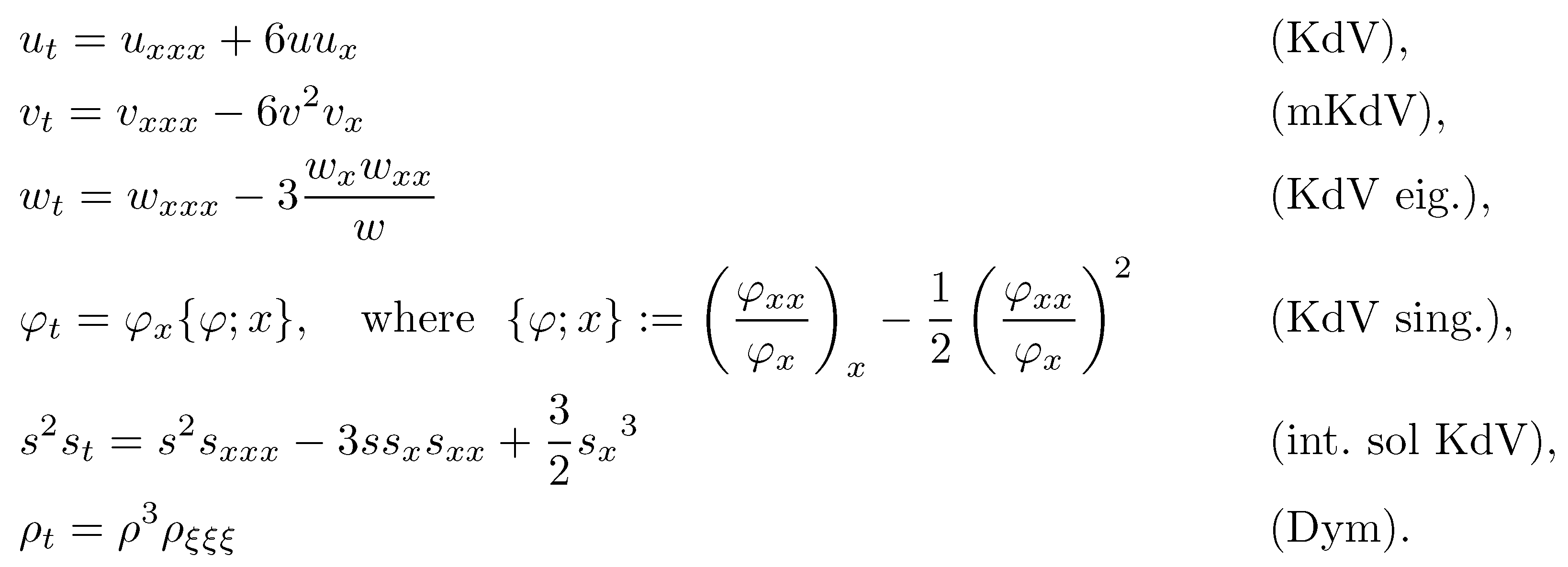
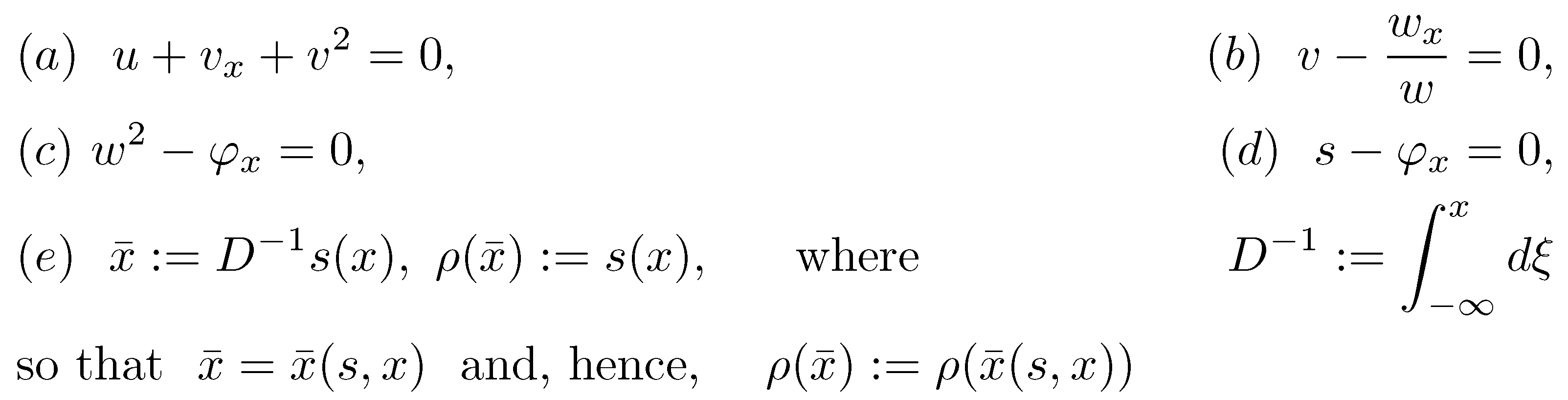
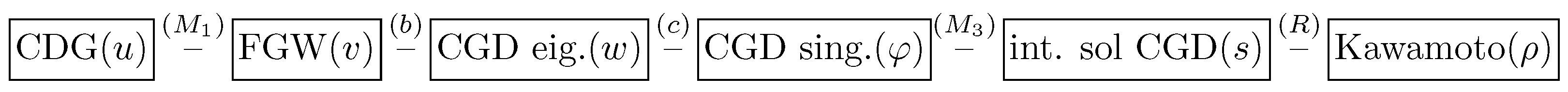
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carillo, S.; Schiebold, C.; Zullo, F. Nonlinear Evolution Equations of the Soliton Type: Old and New Results. Proceedings 2025, 123, 9. https://doi.org/10.3390/proceedings2025123009
Carillo S, Schiebold C, Zullo F. Nonlinear Evolution Equations of the Soliton Type: Old and New Results. Proceedings. 2025; 123(1):9. https://doi.org/10.3390/proceedings2025123009
Chicago/Turabian StyleCarillo, Sandra, Cornelia Schiebold, and Federico Zullo. 2025. "Nonlinear Evolution Equations of the Soliton Type: Old and New Results" Proceedings 123, no. 1: 9. https://doi.org/10.3390/proceedings2025123009
APA StyleCarillo, S., Schiebold, C., & Zullo, F. (2025). Nonlinear Evolution Equations of the Soliton Type: Old and New Results. Proceedings, 123(1), 9. https://doi.org/10.3390/proceedings2025123009







