Abstract
We ask whether there exist non-isomorphic trace monoids over a fixed alphabet that have the same average parallelism. This question is related to the bivariate generating series which counts traces by their height and length; trace monoids with the same also possess the same average parallelism. The series is known to be rational and has been calculated efficiently via the symmetries of the dependence graph, when the latter is connected. We investigate the existence of non-isomorphic dependence graphs (over a common fixed alphabet) with the same series . Using fractional graph isomorphisms and certain equitable partitions of the Cartier-Foata clique automaton, we prove two classification results. First, we show that all-regular independence graphs of the same order share the same generating series if and only if they have the same number of triangular connected components. Secondly, for any , all triangle-free -regular independence graphs of the same order—except for the complete bipartite graph —share this property. The smallest instance of this result for is the pair consisting of the cube graph and the Wagner graph , both on eight vertices.
1. Introduction
Trace monoids [1] model the occurrence of events in concurrent systems. Given a finite alphabet whose letters correspond to actions/events, certain letters commute when the corresponding actions can occur simultaneously, and certain others do not, when the actions can only run sequentially. Mathematically this is described with two binary relations on : a reflexive and symmetric relation called dependence relation, and its complement in called independence relation. Both these can be visualized by their corresponding graphs and The former may be viewed as an undirected graph with loops, called Dependence Graph (DG), and the latter as an undirected loopless graph, called Independence Graph (IG). A loop or self-loop in a graph is a reflexive edge, i.e., an edge that connects a vertex to itself.
The trace monoid is then defined as the quotient of the free monoid by the least congruence that contains the independence relation The elements of are called traces. Two strings in are representatives of the same trace if one can be obtained from the other by repeatedly commuting independent adjacent letters.
Two basic performance measures of a trace are its sequential execution time or length and its parallel execution time or height . The former is simply the length of as a string in whereas the latter is defined as follows. A clique is simply a trace whose letters are mutually independent. Cliques are clearly in one-to-one correspondence to complete subgraphs (also called cliques in graph theory) of the IG Let denote the set of cliques in . An ordered pair is called Cartier-Foata (CF-) admissible [2] if for every letter of there exists a letter of such that We will extensively use the negation of this condition: a pair is not CF-admissible if there exists a letter of such that for every letter of we have The Cartier-Foata (CF) decomposition of a trace is the uniquely defined sequence of cliques such that and each pair is CF-admissible, for all The height of is then just the positive integer in this decomposition.
Example 1.
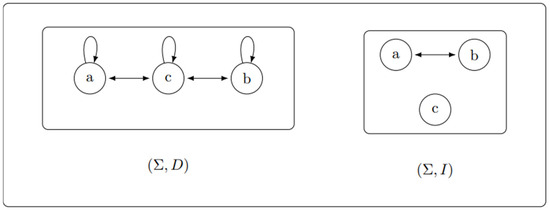
Let We define the dependence relation on the independence relation is . The corresponding dependence graph is the path graph (if we ignore the loops). Both the dependence graph and the corresponding independence graph are shown in Figure 1. In the trace monoid the strings and are both representatives of the same trace

Figure 1.
The dependence graph (on the left column) and the corresponding independence graph (on the right column) of the trace monoid defined in Example 1.
For a trace monoid the bivariate generating series of height and length is defined as
on two commuting variables and It codifies the enumeration of all traces in of given height and length. Suitable specializations of the series are the length and the height generating series, denoted by and , respectively. These are defined as
It is known [2] (Chapter II) that is a rational series. In particular it is equal to the inverse of the Möbius polynomial a signed version of the clique polynomial of the IG
In this paper, we focus on the following question:
Problem 1. Can we find two non-isomorphic connected dependence graphs and over a fixed alphabet which have the same generating series of height and length, i.e., =
Remark 1.
The main motivation to study this problem is the fact that equality of the generating series yields an affirmative answer to the question of finding different concurrent systems over a given set of actions/events that share the same amount of parallelism. This is clearly equivalent to finding non-isomorphic dependence graphs over the same alphabet whose corresponding trace monoids have the same amount of parallelism. Such a measure is a certain real number in the interval which can be viewed as a percentage, by multiplying it with
In the free commutative case (when the IG is the complete graph) this number is equal to
In general, the more such measure is closer to 1, the more parallel the corresponding concurrent system is.
It is easy to see that trace monoids over a fixed alphabet which share the same bivariate generating series of height and length also share the same average parallelism. Indeed, two of the several measures of average parallelism in a trace monoid are the (asymptotic) average height for the uniform probability distribution over the set of all traces of length and the (asymptotic) average length for the uniform probability distribution over the set of all traces of height Let be the coefficient of in , i.e., the number of all traces of height and length and be the set of non-negative integers. Then and are defined respectively as the limits , and It turns out that for every trace monoid both limits always exist, and are in fact algebraic numbers [3] (Section 5.2). Now, for two DGs and over a common alphabet it is obvious that if = , then and as both limits depend entirely upon the coefficients which are identical for both trace monoids.
To our knowledge, an explicit pair of non-isomorphic DGs over a common alphabet that share the same generating series of height and length has not yet been found, and moreover, so far, there is no relevant theory that can lead to some general results in this direction. This paper tackles for the first time this topic, which is of interest both for the algebraic graph theory and the concurrency theory community. Of particular interest to us in this work are the common graph theoretical features of all dependence (independence) graphs whose trace monoids share the same generating series of height and length.
Problem 1 can be also posed for the height generating function On the other hand, its version for the length generating series is immediately solved as = if and only if the IGs and possess the same clique polynomial. This necessary condition allows us to rephrase the above problem with respect to IGs in the following way:
Problem 2. Can we find two non-isomorphic independence graphs and over a fixed alphabet with the same clique polynomial and connected complementary dependence graphs and , such that
As the cliques of the complement of a graph are also known as independence sets and the corresponding clique polynomial of the complementary graph is known as independence polynomial, Problem 2 can alternatively be stated in the form:
Problem 3. Can we find two non-isomorphic connected dependence graphs and over a fixed alphabet with the same independence polynomial, such that
In the sequel we will further study these and justify why we impose the connectedness condition on DGs, in the statement of the problems posed.
2. The Digraph of Cliques and Its Symmetries
The digraph of cliques (DGC) is the directed graph with the set of cliques as nodes and the set of all CF-admissible pairs as its arcs. It contains the DG as a subgraph, and every node in it has a loop. is in general complicated and looks like a maze. In certain cases it might be more convenient to apply the negation of the CF-admissibility condition and construct the complement of the digraph of cliques (CDGC), a loopless digraph which now contains the IG It has been proved in [3] that if the DG is connected, then the DGC is strongly connected. In practice this means that for any given cliques and there exists at least one trace in whose first factor in its CF-decomposition is and the last is In this way, the enumeration of all traces of given height and given length is equivalent to the enumeration of all paths in of length and total weight
Example 2.
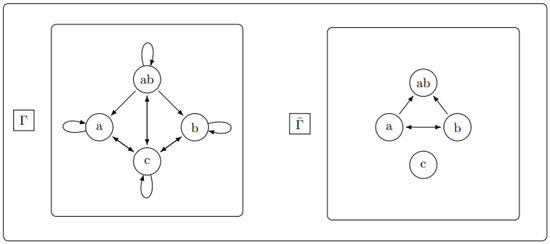
Consider the trace monoid defined in Example 1. The set of cliques is
The CF-decomposition of is and therefore its height and length are respectively and The corresponding digraph of cliques and its complement are shown in Figure 2.

Figure 2.
The digraph of cliques (on the left column) and its complement (on the right column) of the trace monoid defined in Example 1. Observe that and are subgraphs of and respectively. Furthermore, is clearly less complicated than In fact, one can start from the negation of CF-admissibility conditions, obtain and then consider its complement .
Following a reduction technique for multi-digraphs [4] (Chapter 4), we partition the nodes of the digraph of cliques based on their direct successors. An Equitable Partition (EP) of is a partition of in parts (cells) with the property that for all , the number of direct successors that a node in has to is independent of the choice of the original node in . The notion of an EP of a multi-digraph is a generalization of the usual notion of an EP for a simple undirected graph [5] (Section 9.3). To distinguish between those, what is defined here as EP is also known as out-equitable partition for digraphs in recent literature, e.g., see [6].
For technical reasons, for each we set and define the vector as Additionally, we impose the condition that all cliques in the cell have the same length The corresponding matrix is called Coloration Matrix (CM) of . In the special case of an EP of an undirected graph, the CM is also known as quotient matrix.
Remark 2.
In many cases, to show that a partition of the DGC
is equitable, it is easier to use the negation of CF-admissibility condition and show that for any
the number
of its direct successors in
the CDGC
to
, is independent of the original choice of
This immediately implies that the corresponding number
of direct successors in
that a node in
has to
is also independent of the choice of
as clearly
for any
If we set
=, this implies that
or in pure matrix form
where
is the all-ones column vector.
A natural family of EPs of the DGC that preserves the length of cliques in their cells, is the one induced by non-trivial subgroups of its full automorphism group. Due to the complex structure of , finding its automorphisms is extremely difficult. But since any automorphism of the dependence graph of the dependence graph induces the automorphism of the digraph of cliques , where for a clique , we may restrict to the symmetries of the DG
One of the main results in [3] is the following theorem that effectively computes the generating series in terms of the aforementioned CM. Let us first define the associated monomial CM = , and the column monomial vector .
Theorem 1.
[3] (p. 137). Let
be an equitable partition of the DGC
of the trace monoid
on a connected DG
where all cliques in each cell
have the same length
Then the generating function of height and length
is rational and is given by the formula
Example 3.
We keep studying the model of Examples 1 and 2. Consider the partition
of defined by and . It is easily checked to be equitable; in fact, it is an orbit partition induced from the automorphism of order two of the independence graph that exchanges with and keeps fixed. Observe that in this example we have
;
and
The corresponding coloration matrix is
and the associated monomial CM is .
Theorem 1 then yields the decomposition
.
Calculating the inverse matrix, we finally obtain the bivariate generating series
The Taylor expansion of the series
around the point
as can be confirmed by a Python 3.13 script, is
For instance, there are traces of height and length (one can easily check that these are in fact the traces and traces of height and length
In view of Theorem 1, it is clear that if the digraphs of cliques and of two dependence graphs and have EPs and of the same type, i.e., and , with equal CMs , then the generating series of their corresponding trace monoids are equal, i.e., . Note that the converse might not hold. Ιt is therefore natural to ask the following question.
Problem 4. Can we find two non-isomorphic connected dependence graphs and over a fixed alphabet with the property that their corresponding digraph of cliques and have equitable partitions of the same type, and in particular with the same coloration matrix?
Remark 3.
At this point we should mention that there is one extra measure of asymptotic average parallelism, that both trace monoids in Problem 3, share, namely the asymptotic average height
on the uniform probability on CF-decompositions. The way this probability distribution is defined is the following: given a trace of height we get a trace of height by picking at random and uniformly a CF-admissible clique and by setting The quantity is then defined as the limit where is the average length of traces of height obtained from the uniform probability on CF-decompositions [3] (Section 5.3). Νormalizing the CM we obtain the Markovian matrix , where = Since is connected, Lemma 1 implies that is an irreducible matrix, so that Perron-Frobenius theorem yields a unique probability vector such that = . It turns out that always exists, is a rational number, and using the ergodic theorem on Markov chains [7] (Theorem 4.7), it is given by the formula
Now clearly, when two connected DGs share the same CM for EPs of the same type, (5) yields their common asymptotic average height
3. Results
The statement of Problem 3 and the requirement for equitable partitions (EPs) of the same type and equal Coloration Matrices (CMs) on the corresponding Digraphs of Cliques (DGCs), is reminiscent of the notion of common EP that is a necessary and sufficient criterion for fractionally isomorphic simple graphs.
Two simple undirected graphs and with adjacency matrices and are called fractionally isomorphic, denoted by if there exists a doubly stochastic matrix (a square matrix with non-negative entries whose rows and columns all sum to such that [8] (Section 6.1). This definition is a relaxation of the one for isomorphic graphs, as in that special case, the required doubly stochastic matrix is simply a permutation matrix (a -matrix with a unique in each row and column). Two fractionally isomorphic graphs share several common graph theoretical properties: e.g., they have the same order, size, and degree sequence. They also have the same index (the maximum eigenvalue of the adjacency matrix), although they might not be co-spectral (share the entire set of their adjacency eigenvalues).
There is a beautiful connection between fractional isomorphic graphs and EPs of their vertices [8] (Section 6.3). The discrete partition with cells all the singletons containing each vertex is always an EP. On the other hand, the partition with only one cell containing all the vertices is an EP if and only if the graph is regular. The coarsest equitable partition is an EP with the fewest possible number of cells. It is proven to be unique and can be computed with the Weisfeiler-Leman (WL-)algorithm [9], which iteratively refines a given coloring of the vertices of an input graph, until a stable coloring is reached. For a more contemporary discussion on the WL-algorithm, its generalizations, and its usage in machine learning with graphs see [10].
We say that two simple graphs and have a common equitable partition if there exist two EPs and in and , respectively, that have the same number of cells; same number of vertices in each cell; and the same quotient matrix.
Theorem 2.
[8] (p. 140). if and only if they have a common equitable partition or equivalently if and only if they have a common coarsest equitable partition.
Since a DG is always a subgraph of its DGC, a lighter version of Problem 4 may be posed in the following way.
Problem 5. Can we find two connected non-isomorphic, fractionally isomorphic dependence graphs over a fixed alphabet that share the same independence polynomial (i.e., their complementary independence graphs have the same clique polynomial)?
If we restrict ourselves to regular graphs of the same order and valency—which have the property that both themselves and their complements are trivially fractionally isomorphic—this question leads to the following easier one.
Problem 6. Can we find two non-isomorphic -regular independence graphs that share the same clique polynomial and their complementary dependence graphs are connected?
We start with a few remarks on the range of the values of the parameter All -regular graphs are isomorphic to the null graph, and all -regular graphs are isomorphic to a graph that consists of disjoint copies of the complete graph . Therefore, Problem 6 is in fact posed for Making the extra assumption that such a graph is triangle-free, we only need to check when its complement is a connected graph.
Our starting point is a well-known statement, although it cannot be found independently in the literature. It is usually derived from other results, e.g., it is related to [11] (Theorem 3).
Lemma 1.
A -regular and triangle-free graph has a disconnected complement if and only if it is the complete bipartite graph
Proof.
For the graph is indeed -regular and triangle-free since it is bipartite. Its complement is clearly disconnected, as it consists of two disjoint copies of the complete graph Conversely, let be any -regular and triangle-free graph on vertices, with a disconnected complement Then for some First observe that we must have as otherwise for any vertices and in and respectively, the edges and necessarily belong to the edge set of contradicting the fact that is triangle-free. Now, since both components must be complete graphs. Indeed, suppose that one of these, without loss of generality is not a complete graph. Then there exist two vertices in , such that the edge lies in . and for any vertex in a triangle formed by and is a subgraph of giving once more a contradiction. Therefore , with Since is also regular of degree we must have Then we obtain which yields and and therefore we finally obtain □
We are now ready to state our first result, which surprisingly yields a whole special family of regular graphs as solutions to Problem 4.
Theorem 3.
All -regular triangle-free (independence graphs over a common given alphabet
—except for the complete bipartite graph
—always have the same
coloration matrix, with respect to the equitable partition of the corresponding digraphs of cliques
with cells the vertices and edges of the independence graph.
Proof.
By Lemma 1, the complement of any -regular triangle-free IG which is not isomorphic to is a connected graph. Consider the partition of the cliques of , whose cells are the vertex set and the edge set in If then , since is -regular. We will show that is an EP and its CM for the DGC of the corresponding DG will depend only on the order and the degree of .
We use the negation of CF-admissibility and construct the CDGC of the DGC . Consider an arbitrary vertex of . It is clear that it will have neighbors in , and hence other vertices as its direct successors in ; let us denote them by Let us now count all edges that are direct successors of in We claim that in total there exist exactly such connections. These in fact correspond to the incident edges to the vertex and to all other edges that are incident to vertices i.e., the edges of the form
All edges in (6) are distinct to each other, since would yield and and this would imply that is an edge, a contradiction since we would then have the triangle with vertices in Therefore, in total, we have direct successors from an arbitrary given vertex to the set of edges (2-cliques) in On the other hand, there is clearly no direct successor in from an edge to either a vertex or any edge. This analysis yields the matrix therefore by Formula (3) the CM of the DGC is equal to
The entries of this coloration matrix clearly depend only on the parameters and , as required. □
The smallest pair of -regular (cubic) IGs that have the same CM, and therefore the same generating series of height and length , consists of the cube , and the Wagner graph , and is depicted in Figure 3. Note that the former is a vertex and edge-transitive graph, whereas the latter is only vertex transitive. Nevertheless, the EP described in the theorem yields the same CM, although it is an orbit EP (is produced from a certain automorphism of the graph) for the former, and a non-orbit EP for the latter. These two graphs are in fact the only triangle-free cubic graphs of order 8. For this particular pair of cubic graphs let us now calculate the commonly shared generating series Substituting and in (7) we obtain the coloration matrix The associated monomial coloration matrix is Now since and Theorem 1 yields
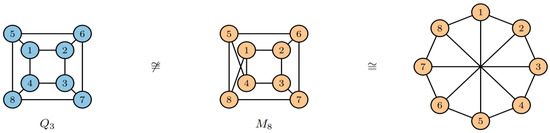
Figure 3.
The smallest pair of cubic triangle-free IGs with the same CM: the cube graph is depicted at the left with blue color, and the Wagner graph is depicted in two different drawings with light orange color. Note that the light orange drawing in the middle is almost identical to the blue one of the cube graph: edges and of the blue drawing are switched to edges and in the middle one.
Calculating the inverse we finally obtain the bivariate generating series
The Taylor expansion of the series around the point as can be confirmed by a Python 3.13 script, is
We can also calculate the commonly shared asymptotic average height on uniform probability on CF-decompositions, for the trace monoids with IGs the graphs and The associated Markovian matrix is
and the corresponding unique probability vector is calculated as 31, 15/31), so that (5) yields
There exist three other connected cubic graphs of order that are not triangle-free, which have distinct clique polynomials, since the number of triangles differs in each one of them [12] (Figure 12). Consequently, the height and length series of their corresponding trace monoids will be distinct.
Our next result deals with the general case of a -regular IG . Such a graph is isomorphic to a disjoint union of cycle graphs for It is therefore clear that two such graphs of the same order share the same clique polynomial if and only if they have the same number of triangular connected components. The complement of such a graph is always connected except form the case where is just a copy of a -cycle, which is isomorphic to the complete bipartite graph this case has been already excluded in view of Lemma 1.
Theorem 4.
Amongst 2-regular independence graphs of the same order those with the same number
of triangular connected components share the same CM, for a suitable EP of the DGC of their DGs.
Proof.
Let be the given IG. Label the triangular components of by and write the vertices of each as We partition the set of cliques into the following five cells:
- all vertices that belong to some triangle
- vertices that lie on non-triangular cycles;
- all edges inside the triangles
- edges of non-triangular cycles; and
- the triangles themselves .
Set We clearly have We use again the negation of CF-admissibility on the CDGC of the DGC . Consider an arbitrary vertex in Let this be, without loss of generality, the vertex It is linked only to its two adjacent vertices , in and to no other vertex of some for or of any larger cycle. It is also linked to the three edges in and to no other edge of some for or of any larger cycle. Finally, it is linked to the unique triangle in . This analysis yields the vector as the 1st row of the matrix
Now consider a vertex , which belongs to an arbitrary circular non-triangular component. As in the previous case, it is linked to its two adjacent vertices and to no other vertices of that cycle, or any other cycle or triangle. It will also be linked to four of its edges, namely to its two incident edges , and to two more incident edges , to its neighbors . This shows that the 2nd row of is the vector
Consider an arbitrary edge in and without loss of generality let this be the edge in There is only one vertex in such that this edge is linked, namely the vertex It is also linked only to the edges and in and only to the triangle in . This shows that the 3rd row of is the vector
Finally, any edge in or any triangle in has no links to any element of the given partition, so the 4th and 5th row of will be both equal to the zero vector. Concluding, we obtain the matrix so by (3) or (4), the CM that corresponds to the EP of the DGC is equal to
As this matrix depends only on the parameters and , which are common for all such IGs, the result follows. □
In Figure 4 below we give the smallest example, with respect to the order of graphs, of two such 2-regular independence graphs, as mentioned in Theorem 4.
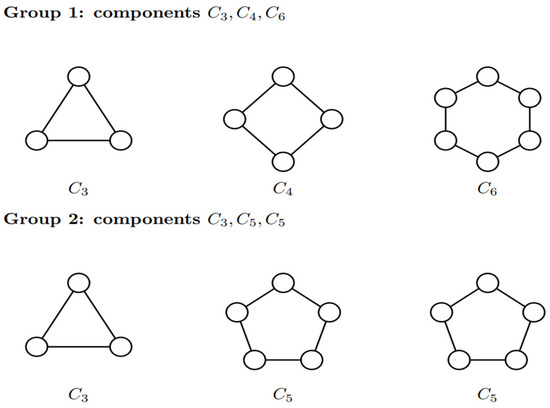
Figure 4.
The smallest pair (of order ) of 2-regular non-isomorphic IGs with only one triangular component; according to Theorem 4 both graphs have the same CM. The one in the first row has also one copy of the cycle and the cycle whereas the one in the second row has two extra copies of the cycle .
4. Conclusions and Further Research
In this paper we have studied the problem of finding non-isomorphic connected Dependence Graphs (DGs) over the same alphabet with the property that their corresponding trace monoids have the same generating series of height and length. A necessary condition for this is that their corresponding Independence Graphs (IGs) must share the same clique polynomial. The main practical significance of this study is the construction of parallel systems that have the same amount of average parallelism; we have seen this for three distinct such measures. The calculation of had been efficiently done in terms of the Digraph of Cliques (DGC), which depicts the Cartier-Foata (CF-)admissibility condition (or of the complement of the digraph of cliques (CDGC) that depicts the negation of CF-admissibility), exploiting its symmetries. In this way, two DGs with DGCs that have Equitable Partitions (EPs) of the same type and same Coloration Matrix (CM) have the same series This is reminiscent of the notion of common EP, which is a well-known necessary and sufficient condition for two simple graphs to be fractionally isomorphic.
Exploiting this idea in the special case of -regular IGs we have fully studied the case , proving that two -regular non-isomorphic IGs have the same coloration matrix if and only if they have the same number of triangular connected components. Restricting to the special case of triangle-free graphs, we have shown that for any , two -regular triangle-free IGs—which are different from the complete bipartite graph - have always the same CM for their trace monoids.
Further research work underway might include the following:
Suppose that we have two fractionally isomorphic and connected dependence graphs over the same alphabet that share the same independence polynomial and consider their digraph of cliques. Does there exist an algorithm which decides about the existence or not of equitable partitions of the digraph of cliques, that are of the same type with the same coloration matrix? What could be inferred about the complexity of such an algorithm? It seems that Paige and Tarjan’s algorithm [13], a well-known partition refinement procedure, or some variation of it, would be the basis of such an algorithm. In [14] these notions are extended to arbitrary relational structures, which include directed graphs as a specific case. Furthermore, the WL-algorithm’s iterative refinement process can be applied to such structures to test for a broader aspect of fractional isomorphism. It seems that the suitable concept that extends the notion of fractional isomorphism from undirected to directed graphs and their out-equitable partitions, is the notion of row/left fractional isomorphism.
If we restrict ourselves to regular graphs, can we say more than what was presented here? For cubic graphs, in particular, this seems quite promising, as there is a very rich theory [12] which could be combined with our findings so far and possibly extend them to promising new results.
In this paper we have treated partially the case of regular graphs. We are not yet sure how our methods might extend to non-regular graphs. Quite recently, we have managed to find pairs of non-regular graphs that are solutions to Problem 5, i.e., fractionally isomorphic connected non-regular graphs with the same independence polynomial. Determining whether the digraphs of cliques of these pairs admit equitable partitions of the same type with the same CM, or whether the corresponding trace monoids share the same generating series, is work in progress.
Author Contributions
Conceptualization, resources, writing-review and editing, supervision, methodology, project administration I.M.; methodology, software, validation, formal analysis, C.K.; investigation, resources, data curation, writing—original draft preparation, I.M.; writing—review and editing, visualization, C.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DG | Dependence Graph |
| IG | Independence Graph |
| DGC | Digraph of Cliques |
| CDGC | Complement of Digraph of Cliques |
| EP | Equitable Partition |
| CM | Coloration Matrix |
References
- Diekert, V.; Rozenberg, G. (Eds.) The Book of Traces; World Scientific: Singapore, 1995. [Google Scholar]
- Cartier, P.; Foata, D. Problèmes combinatoires de commutation et rearrangements. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1969; Volume 85. [Google Scholar]
- Krob, D.; Mairesse, J.; Michos, I. Computing the average parallelism in trace monoids. Discret. Math. 2003, 273, 131–162. [Google Scholar] [CrossRef]
- Cvetkovic, D.; Doob, M.; Sachs, H. Spectra of Graphs. In Theory and Applications, Pure and Applied Mathematics; Wiley: Paris, France, 1980; Volume 87. [Google Scholar]
- Godsil, C.; Royle, G.F. Algebraic Graph Theory, Graduate Text in Mathematics; Springer Science and Business Media: New York, NK, USA, 2001; Volume 207. [Google Scholar]
- Deng, A.; Sato, I.; Wu, Y. Homomorphisms, representations and characteristic polynomials of digraphs. Linear Algebra Its Appl. 2007, 423, 386–407. [Google Scholar] [CrossRef]
- Seneta, E. Non-Negative Matrices and Markov Chains, 2nd ed.; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Scheinerman, E.R.; Ullman, D.H. Fractional Graph Theory, A Rational Approach to the Theory of Graphs; Dover Publications, Inc.: Mineola, NY, USA, 1997. [Google Scholar]
- Weisfeiler, B.; Leman, A.A. A reduction of a Graph to a Canonical Form and an Algebra Arising during This Reduction. Nauchno-Tech. Informatsia. 1968, 2, 12–16. [Google Scholar]
- Morris, C.; Lipman, Y.; Maron, H.; Rieck, B.; Kriege, N.M.; Grohe, M.; Fey, M.; Borgwardt, K. Weisfeiler and Leman go Machine Learning: The Story so far. J. Mach. Learn. Res. 2023, 23, 15865–15923. [Google Scholar]
- Chung, M.-D.; West, D.B. Large P4-free graphs with bounded degree. J. Graph. Theory 1993, 17, 109–116. [Google Scholar] [CrossRef]
- Greenlaw, R.; Petreschi, R. Cubic graphs. ACM Comput. Surv. (CSUR) 1995, 27, 471–495. [Google Scholar] [CrossRef]
- Paige, R.; Tarjan, R.E. Three Partition Refinement Algorithms. Siam J. Comput. 1987, 16, 973–989. [Google Scholar] [CrossRef]
- Butti, S.; Dalmau, V. Fractional homomorphism, Weisfeiler-Leman invariance, and the Sherali-Adams hierarchy for the Constraint Satisfaction Problem. In Leibniz International Proceedings in Informatics (LIPIcs), Proceedings of the 46th International Symposium on Mathematical Foundations of Computer Science (MFCS 2021), Tallinn, Estonia, 23–27 August 2021; Schloss Dagsthul—Leibniz-Zentrum für Informatik: Wadern, Germany, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).