Chemical Equitable Partitions: A New Perspective on Molecular Symmetries and Its Implications for the Study of Structure–Property Relationships ^†

Abstract

In this work, the concept of equitable partition is applied to molecular graphs to define quantitative descriptors of the symmetry and complexity of molecules, with the ultimate goal of shedding new light on the structure–property relationships of chemical compounds and materials. The ways in which symmetry is reflected in these descriptors and their correlations with molecular properties are demonstrated using simple examples, and their potential for the prediction of properties of complex molecules is underscored.

1. Introduction

Structure–property relationships are of great interest in chemistry and materials science. Symmetries of molecules, as well as those of crystal lattices, play a pivotal role in this context. Group theory applied to molecular and crystal symmetries is an established field that has been very successful in the description of the symmetry elements of molecules and crystal lattices. However, it would be advantageous to have quantitative measures of symmetry that could be directly correlated with values of physical properties.

To derive quantitative descriptors of symmetry, we begin with the observation that the representations of symmetrical species, such as the various chemical formulas, can be reduced to more condensed forms with minimal information content. The mathematical branch of Algebraic Graph Theory offers a systematic approach to map molecular representations to compressed forms, while respecting the special roles of atoms, or groups of atoms in the molecular topology. This topic and its implications are explored in the present article.

A graph G(V, E) is a collection of nodes or vertices, V, and a set of edges, E, that represent connections or relationships between the vertices. The connectivity in a graph is summarized by its adjacency matrix A, a square symmetric matrix that has non-zero or zero elements A_ij, depending on whether the corresponding vertices i and j are connected (adjacent) or disconnected (non-adjacent), respectively [1,2].

Using graph-like schemes to depict organic molecules is a familiar concept: bonds can be seen as edges, whereas bonded atoms are the graph’s adjacent vertices [3]. Apart from this neat correspondence between syntactic formulas and graphs, chemical graph theory has also emerged from the observation that the energy levels of the semiempirical Hamiltonian of polyaromatic compounds can be mapped to the eigenvalues of the molecular adjacency matrix, defined by the heavy atoms taken as graph vertices [2] (pp. 228–251). The corresponding mathematical derivation implies that the entries of the adjacency matrix should be assigned only the values of 1 and 0. However, it is also possible to introduce bond orders as edge weights, which are also the values of the corresponding adjacency matrix elements, in the quest for more flexible graph-theoretic schemes.

Notably, the graphs defined as above are undirected (weighted or unweighted) meaning that the edges merely connect the vertices; there is no sense of direction from one vertex to another. Chemical valence is in direct correspondence to vertex degree, the number of edges connecting a given vertex v to other vertices, or the sum of weights over those edges, if the graph is weighted. Finally, it is possible to define graphs for the unit cells or appropriate supercells of crystal lattices; in that case, vertex degrees correspond to the ions’ coordination numbers [4,5].

2. Materials and Methods

Symmetry in molecules is a topic that has been studied thoroughly, leading to accurate description of the molecules’ spatial arrangements with the aid of symmetry elements (inversion, rotation, etc.). Molecular symmetries are partly reflected in the topology or connectivity of the corresponding graphs. Thus, graph nodes can be grouped together when sharing a common connectivity profile. This leads to the concept of Equitable Partition, which is key in the application of graph theory to molecular symmetries, due to the fact that it can describe generalized graph symmetries (i.e., not exclusively related to graph automorphisms) [2,6].

Given a graph G(V, E), we can partition its nodes into s non-overlapping subsets V_i, i = 1, 2, …, s, such that their union restores the original set without omitting any nodes: ${\cup }_{i=1}^s{V}_i=V$. The collection of these subsets is a partition P(V) of V. Then, a given partition of V is an Equitable Partition (EP) when nodes in a subset V_i (also called a cell of the partition) have the same fixed number, b_ij, of adjacent neighbours in a cell V_j for all possible pairs of i and j (including the case i = j). The collection of all b_ij, j = 1, 2, …, s, of any vertex in any cell V_i is the connectivity profile of that vertex with respect to the given EP. Therefore, EP classifies graph vertices in such a manner that vertices in the same cell have the same connectivity profile. As a corollary, they also have the same vertex degree equal to the sum of b_ij over all j.

An EP of a graph can be depicted with a new graph, where cells play the role of nodes. This is the Quotient Graph of G with respect to the given EP, denoted by QG(G, EP). Generally, b_ij may differ from b_ji, so the resultant adjacency matrix, known as quotient matrix, is non-symmetric, and a sense of directionality is introduced: instead of an edge between cells i and j, we have a pair of arcs directed from i to j and vice versa, weighted by the corresponding connectivity numbers b_ij and b_ji. In other words, a QG with respect to an EP is a weighted directed graph. Graphs with rich symmetry have smaller and simpler QGs; the quantification of QG’s size and complexity with respect to the original graph is a pillar of the present research.

A graph can have more than one EPs, forming a hierarchy with coarser partitions refined by splitting one or more cells to give finer EPs. An EP of a graph G that is not a refinement of any other EP can be shown to be unique [7] and is called the coarsest EP (cEP) of G. The cEP itself comes about as a refinement of the partition of vertices, based on their degrees. However, it is perfectly acceptable to choose another partition P as a starting point and find the (provably unique [7]) coarsest EP that refines P, cEP(G, P).

In the present work, we consider the Chemical Partition (CP) of a given molecular graph, G, obtained by partitioning the graph nodes according to their chemical identity and valence. Then, we define the Chemical Equitable Partition (CEP) of G as the coarsest EP that refines CP. We can express this concept schematically as shown below:

CEP = cEP(G, CP).

(1)

The resultant partition is the most ‘economical’ partition of a molecular graph that manages to retain information about chemical composition and symmetry, as well as topology in general. Figure 1 illustrates the concept with the aid of the simple case of an ethane molecule.

The QG in the example in Figure 1 contains a loop as allowed by the general definition of EP, which includes the possibility i = j, for any cells i and j. Notably, the weight of the loop equals 1, in agreement with the definition of EP and the fact that each carbon atom is connected to exactly one other carbon atom. More generally, the weights of the arcs and loops arising in the QG of an EP are such that the node degree (which is also the chemical valence) of atoms in the molecular graph, is preserved, taken as the sum of the weights of outgoing arcs plus the weights of the loops. In this context, loops can be considered as outgoing arcs that just happen to end in the same cell; thus, they are measured once, unlike some existing definitions where loops are considered as pairs of directed arcs with opposite directions.

To express the change in size and complexity when passing from the molecular graph G to the quotient graph, we can take the number of nodes n_QG in QG as a fraction of the number of nodes n_G in G; however, this definition misses the complexity added by the presence of pairs of arcs, instead of edges, and loops in the quotient graph. Thus, we introduce the ratio of the number of arcs (including loops with each loop counted once), a, over the number of edges, m, as a correction leading to the following definition of the Compression Ratio (CR) [4,5]:

$$\%\mathrm{C}\mathrm{R}=100\times {\displaystyle \frac{n_{QG}}{n_G}}{\displaystyle \frac{a}{m}}.$$

(2)

For example, in the case of ethane (Figure 1), we have n_G = 8, m = 7, n_QG = 2 and a = 3, resulting in CR = 10.71%. Generally, small values of CR indicate species with rich symmetry resulting in smaller and simpler quotient graphs relative to the original molecular graphs; conversely, large values of CR indicate more irregular, asymmetrical graphs.

In fact, it would be perfectly legitimate to use the inverse of the ratios entering expression (2) to align with common definitions of information compression measures used in data science. In this work, we stick with the definition chosen in our previous works [4,5], which came about as an extension of the ‘abstraction ratio’ concept, introduced by Hajiabolhassan et al. [8], as discussed in more detail in [4]. Our definition has the additional merits that it can be understood as a proxy measure of the information-content reduction associated with CEP, thus being comparable to the information content discussed in the next paragraphs; and it results in simpler plots as the ones shown later in this work—a crucial aspect with regard to future machine learning applications, where CR and other graph-theoretic indices could be used as features.

It is worth noting that CEP can be combined with the partitioning of atoms into local groups such as ‘united atoms’ (e.g., methyl and methylene groups taken as single sites) or even coarser groups. In this work, we consider both fully atomistic and united-atom molecular graphs.

An algorithm to determine the cEP of an undirected graph G is a task much akin to color refinement procedure [9], that had been established as an intermediate step in solutions for the wider problem of graph isomorphism [7,10,11,12,13]. This is also applicable in the case of the CEP of a molecular graph. The relevant steps have been described in detail in [4] and they are summarized below:

• Initialization: The CP of the molecule is defined according to the chemical identity and degree of the graph’s vertices.
• Classification: Vertices are categorized according to their connectivity profiles of the most recent partition, P, resulting in a new partition, P’.
• Check for equality: P and P’ are compared.

  ο

  If not identical: Replace P by P’ and go back to the classification step.

  ο

  If identical: Terminate.

The compression ratio characterizes a graph as a whole. It would be beneficial to add a perspective that takes local or partial contributions into account. This is possible by combining CEP with the concept of Information Content, I_G, of a graph, as discussed in [14]. Simply put, this is the sum of Shannon entropy contributions from all the CEP cells, resulting in the following expression:

$$I_G=-\sum _{i=0}^s{p}_i{\mathit{log}}_2{p}_i,$$

(3)

where i runs over all s cells of the graph’s CEP; p_i denotes the probability of occurrence of a vertex belonging to cell i, calculated as the corresponding relative frequency (number of vertices in said cell over n_G); and base-2 logarithm is used in the calculation to yield a result expressed in bits per vertex.

Returning to the example of ethane (Figure 1), we have n_G = 8, n_QG = 2, nodes in first cell = 2 and nodes in second cell = 6; therefore, p₁ = 2/8 = 0.25, p₂ = 6/8 = 0.75, yielding I_G = 0.8113.

3. Results

In this section, results are presented for the broader family of saturated hydrocarbons, which combine a simple chemical composition with a rich topology (linear chains, rings, branched species, and combinations), allowing a clear look at the effect of graph symmetries. First, the foundational concepts are demonstrated for the cases of fully atomistic linear, cyclic, and symmetric branched alkanes; then, the effect of symmetry on properties is demonstrated by looking at fully atomistic and united-atom graphs of linear alkanes; and finally, the extension of the same logic to the family of alkylcycloalkanes as well as various branched alkanes is discussed.

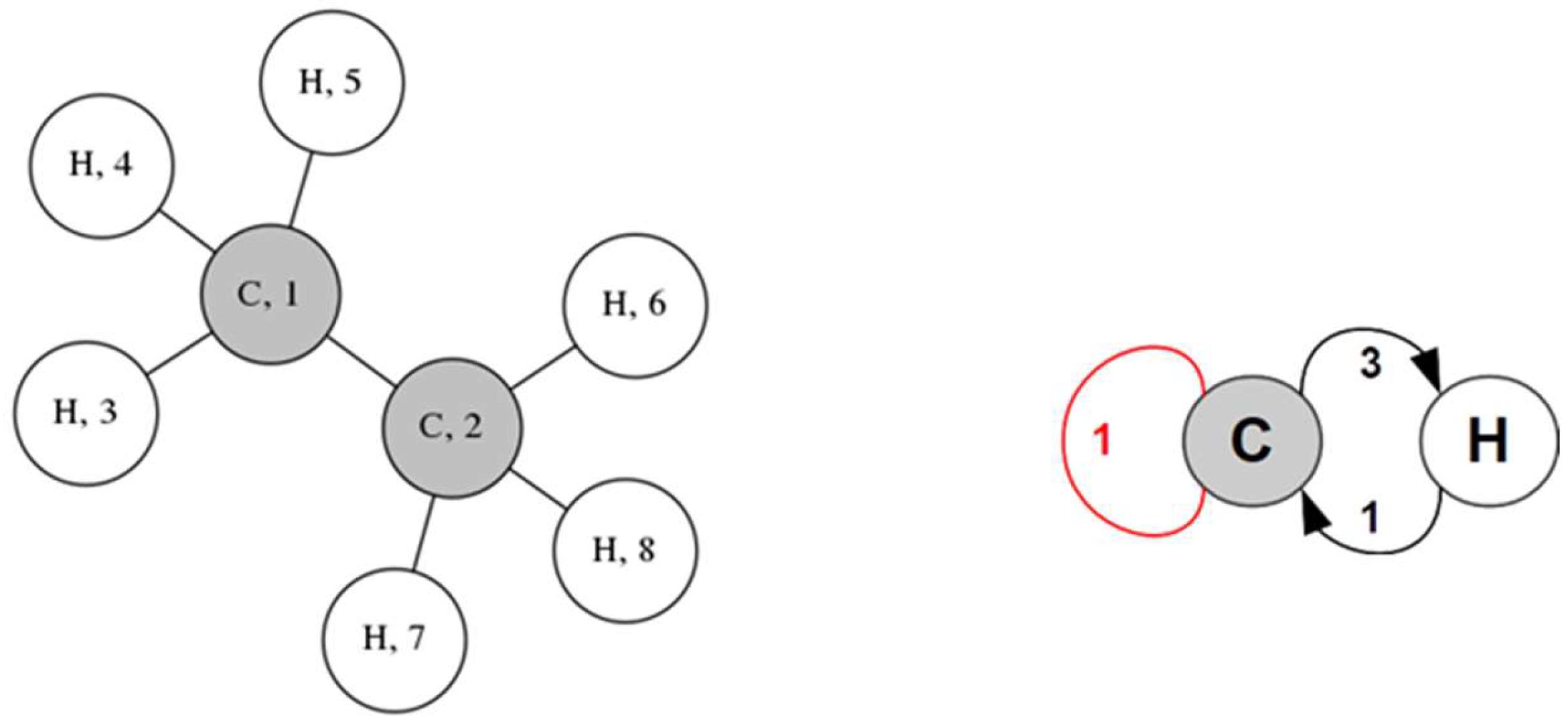
3.1. Demonstration of Foundational Concepts

Figure 2 shows examples of linear, cyclic, and symmetric branched alkanes in their fully atomistic representation, together with their CEP-quotient graphs and the calculated compression ratios.

The following remarks can be made:

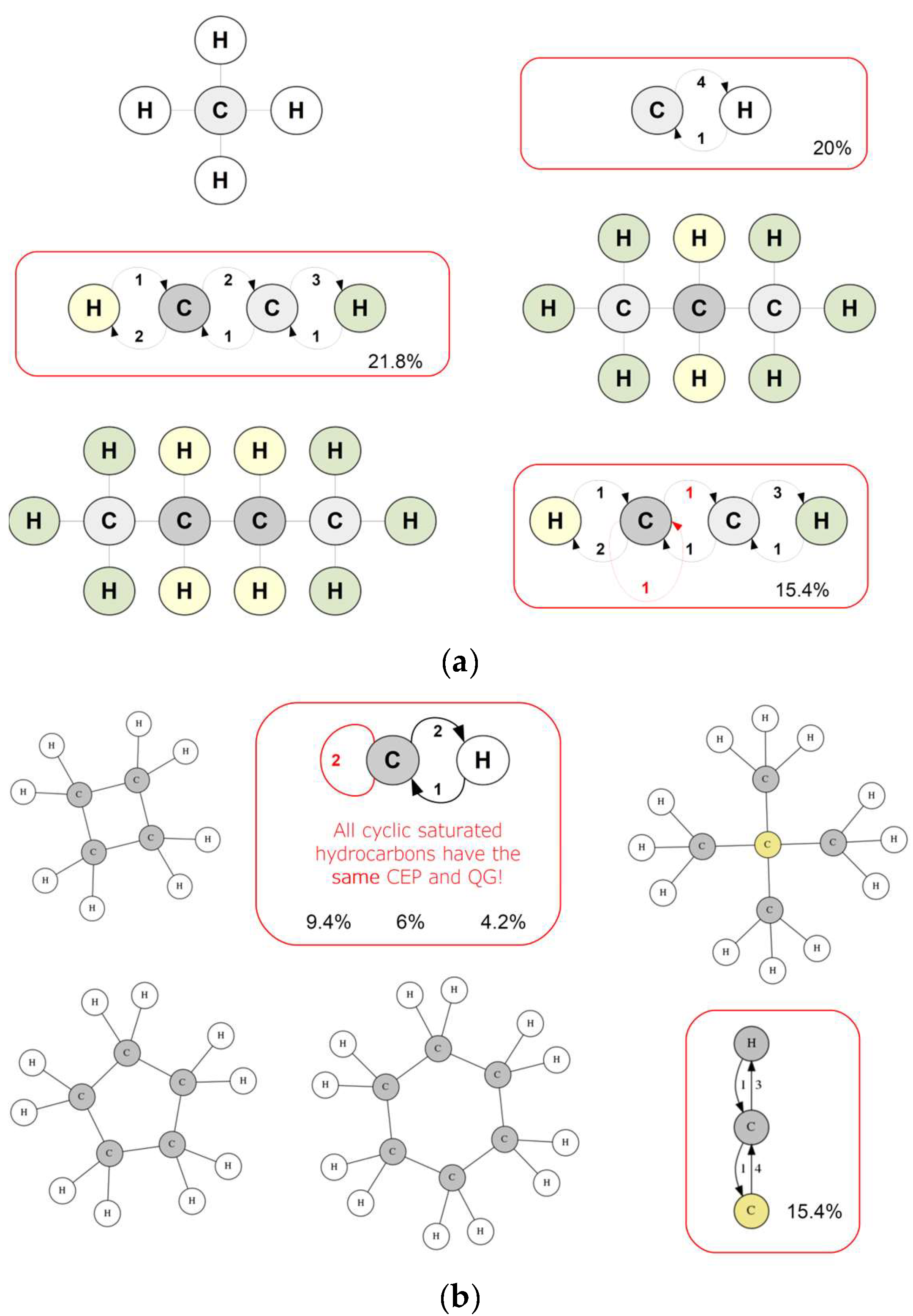
• Linear alkanes present the most complex QGs as atoms are differentiated relative to their distance from the chain ends; notably, there is at most one loop in the QG, depending on whether there is an even or an odd number of carbons.
• Ring alkanes share the same very simple QG, which leads to a decreasing CR with molecular size, reflecting a correspondingly higher symmetry.
• The example of neopentane showcases the effect of symmetry in the form of a small and simple QG relative to a large molecule.

3.2. Molecular Graph Symmetry and Physical Properties

Figure 3 illustrates the interdependence among molecular size, compression ratio, and mass density [15,16] of linear alkanes when looked at in their fully atomistic and united-atom representations.

The following observations can be made:

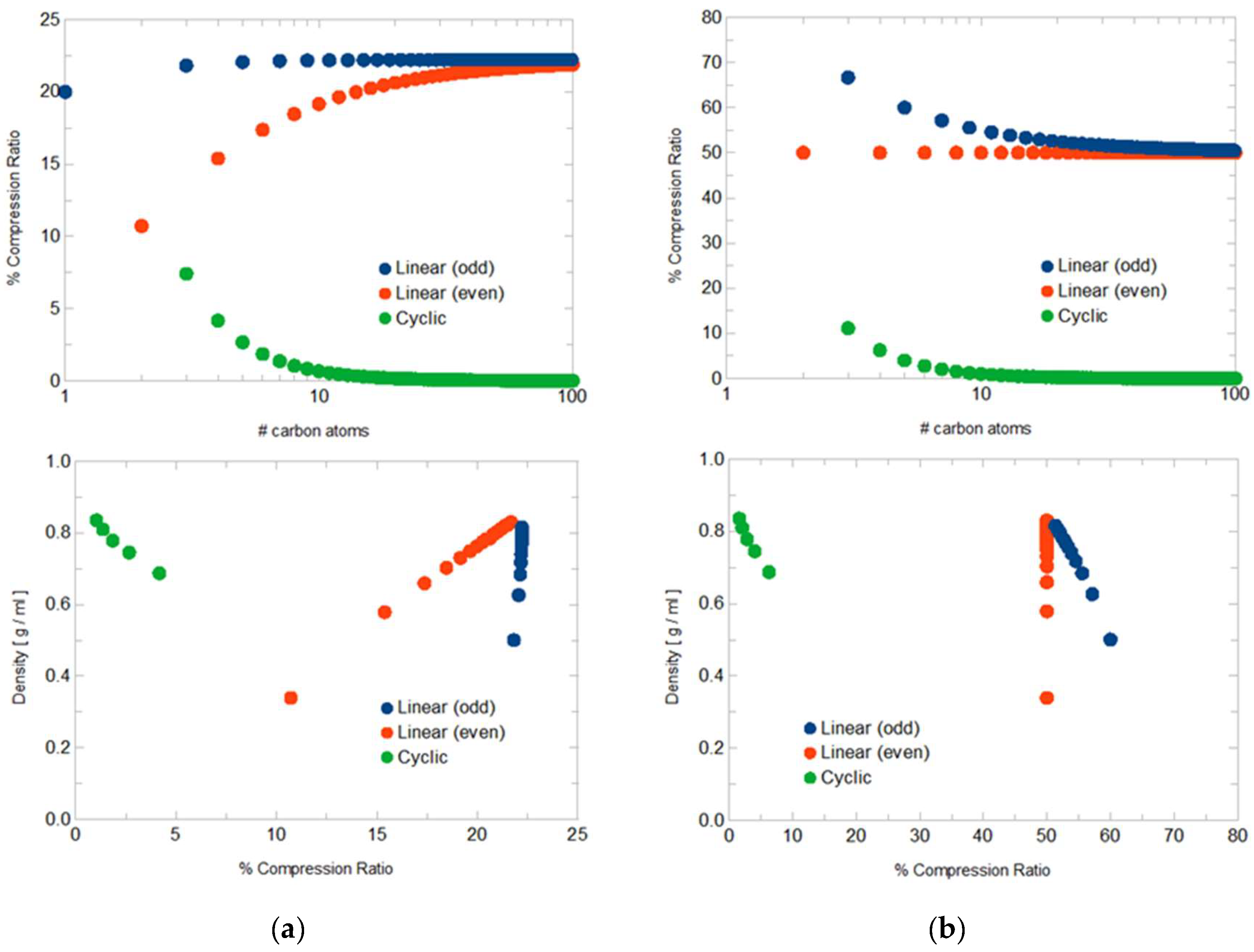
• Cyclic alkanes exhibit a compression ratio tending towards zero in molecular size, as expected, and a relatively clear correlation between CR and mass density.
• United-atom graphs result in higher CR values. The explicit presence of hydrogen atoms implies more information content to compress; omission of hydrogen atoms means that the graphs are already ‘half-compressed’.
• The homologous series of linear alkanes is split into two categories with different correlation between CR and molecular size, or CR and mass density, depending on the even or odd number of carbon atoms. This is due to the presence or not of a loop in the quotient graph, as mentioned in Section 3.1.

3.3. Extension to Complex Topologies

To investigate the effect of symmetry in broader contexts, we generated CR and I_G data for a number of alkylcycloalkanes with rings and alkyl tails of up to 20 carbon atoms each, creating a two-dimensional map. The rationale was that many physical properties can often be approximated by additive schemes bearing some resemblance with the definition of I_G as, for instance, in the case of group-contribution methods [17]. Furthermore I_G, when computed over the cells of CEP, reflects the combined information of chemical composition and topology encoded in the CEP. Then, we assume that I_G can serve as a generic proxy for properties that can be reasonably approximated by additive contributions.

Figure 4 shows the above-mentioned map calculated for alkylcycloalkanes (small-size black dots) in their united-atom representations. On top of it, additional large-sized points with different colours (red, black, orange, and green) are placed, representing various branched alkanes of complex topology. Linear alkanes (medium-sized black dots) and cycloalkanes (large blue points) are also included as limiting cases.

We use the shorthand notation AlkXXCycYY to denote molecules consisting of an alkyl group of XX united atoms (ranging from 00 for zero, to 20) and a cyclic group of YY united atoms (ranging from 00 for zero, to 20). Thus, the family of all molecules containing an XX-long alkyl group is denoted by AlkXX, the part that remains constant for all members of the family. Ring molecules in particular (e.g., cyclopropane, cyclobutene, etc.) are collectively denoted by Alk00 since they have no alkyl group. In a similar vein, the family of all molecules containing a YY-long cyclic group is denoted by CycYY; linear alkanes, in particular, are denoted by Cyc00.

The following observations can be made:

• Cyclic alkanes in their united-atom form have zero information content.
• The addition of an alkyl tail to a ring molecule breaks its symmetry; this is clearly quantified for each molecule by increasing values of CR.
• CycYY families form smooth curves (shown with green colour in the figure) directed roughly from bottom left to top right (except Cyc00), indicating positive correlation of their CR and I_G (increasing information content with increasing asymmetry).
• Cyc00 and AlkYY families form zig-zag lines (shown with dark grey colour); the envelope curves of these lines (denoted by alternating red and blue colour) generally exhibit an anticorrelation between CR and I_G, which becomes more prominent for values of I_G around 2 to 4; and CR around 100 to 150%.
• Linear alkanes and all other alkylcycloalkanes feature an even/odd distinction regarding the number of their carbon atoms, with red and blue envelop lines corresponding to even and odd numbers, respectively. This observation generalises the finding of even-odd distinction in the case of linear alkanes, as discussed in Section 3.2.
• ‘Iso-alkyl’ and ‘iso-ring’ curves are clearly formed by the envelope curves corresponding to different fixed sizes of alkyl tails, and the curves of fixed-size cycloalkyl rings, respectively. These curves, which define a set of ‘chemical coordinates’, are smooth enough to be parameterized as transformations of the (CR, I_G) plane.
• Several branched alkanes tend to cluster parallel to the iso-ring curves. Therefore, it should be possible to model complex molecules using real-valued ‘chemical coordinates’, with the physical significance of fractional contributions of building blocks, e.g., alkyl and cycloalkyl groups, of simpler molecules with known properties.

4. Discussion

Graph theory offers a variety of alternative means and ways to study the structure of molecular and crystal-lattice systems. It provides an arsenal of methods that describe connectivity and topology with quantitative measures. Importantly, it allows measures of symmetry and chemical information through the application of equitable partitioning. Thus, a route opens for structure–property relationships to be elucidated using currently unexplored means that quantify microscopic structure, topology, and symmetry.

Current research work underway includes the following:

• Investigating correlations of more physical properties with graph-theoretic measures, as discussed in Section 3, for larger families of organic compounds.
• Enhancing machine learning schemes for the prediction of physical properties of compounds, by the addition of the above-defined graph theoretic measures and variants.
• Adjusting the above-mentioned methods to inorganic and hybrid organic–inorganic lattices.

Stereoisomers are different embeddings in space of the same abstract graph. By definition, equitable partitions are agnostic to embeddings. Our future goals include the quest for means to overcome limitations in capturing such important aspects of spatial arrangements. Finally, we deem worth considering edge weights that vary continuously according to interatomic separation—this will be particularly useful in the study of lattices as well as intermolecular interactions of dense systems. We trust that the slightest steps in the above directions will greatly enhance our understanding of structure–property relations.