Hybrid Modelling Framework for Reactor Model Discovery Using Artificial Neural Networks Classifiers †
Abstract
1. Introduction
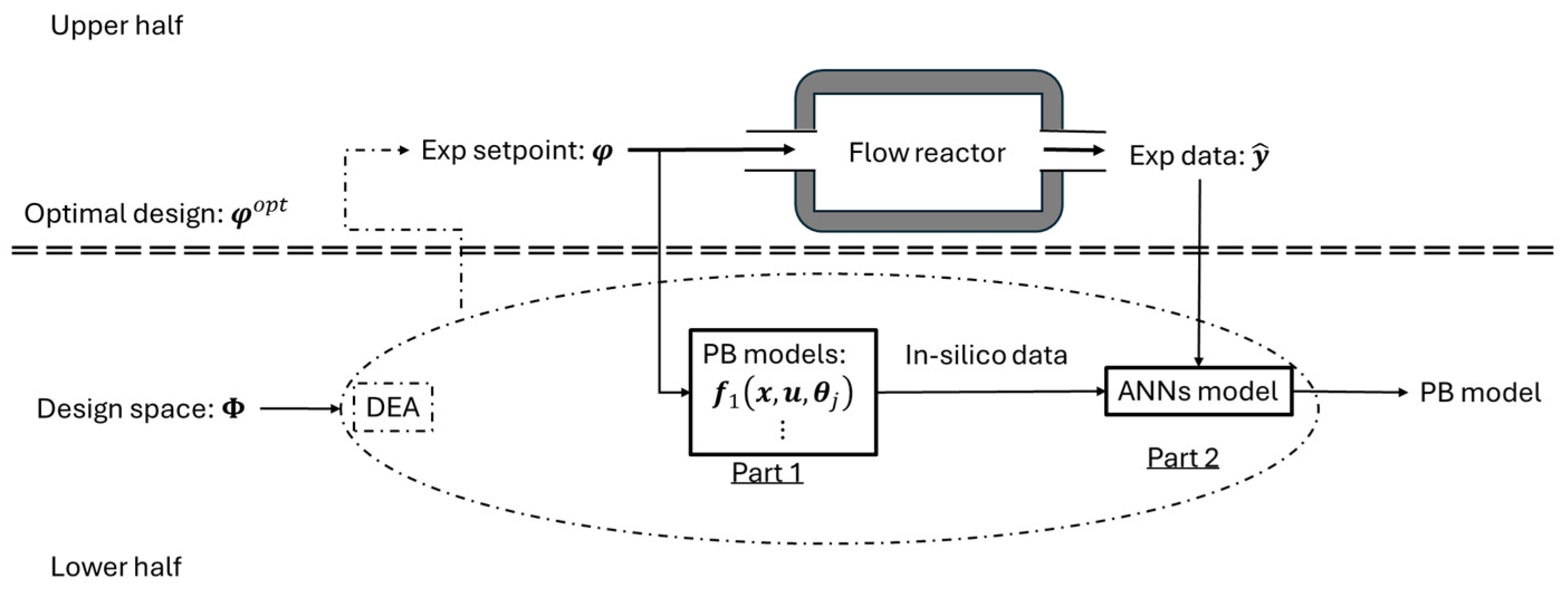
2. Hybrid Modelling Framework
3. Reaction System Case Study
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Machado Cavalcanti, F.; Emilia Kozonoe, C.; André Pacheco, K.; Maria de Brito Alves, R. Application of Artificial Neural Networks to Chemical and Process Engineering. In Deep Learning Applications; Mazzeo, P.L., Spagnolo, P., Eds.; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Quaglio, M.; Roberts, L.R.; Jaapar, M.S.; Fraga, E.S.; Dua, V.; Galvanin, F. An artificial neural network approach to recognise kinetic models from experimental data. Comput. Chem. Eng. 2020, 135, 106759. [Google Scholar] [CrossRef]
- Sangoi, E.; Quaglio, M.; Bezzo, F.; Galvanin, F. An optimal experimental design framework for fast kinetic model identification based on artificial neural networks. Comput. Chem. Eng. 2024, 187, 108752. [Google Scholar] [CrossRef]
- Ranade, V.V. Computational Flow Modeling for Chemical Reactor Engineering; Academic Press: London, UK, 2001. [Google Scholar]
- Waldron, C.; Pankajakshan, A.; Quaglio, M.; Cao, E.; Galvanin, F.; Gavriilidis, A. Closed-Loop Model-Based Design of Experiments for Kinetic Model Discrimination and Parameter Estimation: Benzoic Acid Esterification on a Heterogeneous Catalyst. Ind. Eng. Chem. Res. 2019, 58, 22165–22177. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering; Prentice-Hall: Hoboken, NJ, USA, 2004. [Google Scholar]

| Limits | |||
|---|---|---|---|
| Upper | |||
| Lower |
| Imprecise | |||
| Precise |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agunloye, E.; Gavriilidis, A.; Galvanin, F. Hybrid Modelling Framework for Reactor Model Discovery Using Artificial Neural Networks Classifiers. Proceedings 2025, 121, 11. https://doi.org/10.3390/proceedings2025121011
Agunloye E, Gavriilidis A, Galvanin F. Hybrid Modelling Framework for Reactor Model Discovery Using Artificial Neural Networks Classifiers. Proceedings. 2025; 121(1):11. https://doi.org/10.3390/proceedings2025121011
Chicago/Turabian StyleAgunloye, Emmanuel, Asterios Gavriilidis, and Federico Galvanin. 2025. "Hybrid Modelling Framework for Reactor Model Discovery Using Artificial Neural Networks Classifiers" Proceedings 121, no. 1: 11. https://doi.org/10.3390/proceedings2025121011
APA StyleAgunloye, E., Gavriilidis, A., & Galvanin, F. (2025). Hybrid Modelling Framework for Reactor Model Discovery Using Artificial Neural Networks Classifiers. Proceedings, 121(1), 11. https://doi.org/10.3390/proceedings2025121011







