Charger-Mediated Quantum Batteries ^†

Abstract

We study energy-transfer processes from a given quantum system, termed charger, to another one, i.e., the proper battery both in a closed and in an open quantum setting. We quantify the fraction ${\mathcal{E}}_{\mathrm{B}}\left(\tau \right)$ of energy stored in the battery that can be extracted in order to perform thermodynamic work. We show that there can be a substantial gap between the average energy and the extractable work due to correlations created by charger–battery interactions.

1. Introduction

Quantum phenomena, such as phase coherence and entanglement, constitute remarkable resources that may enable superior performances of future technological devices. Given this context, a number of researchers has been working on quantum batteries [1,2,3], i.e., quantum mechanical systems for storing energy. Here, using the concept of ergotropy [4] we quantify the fraction ${\mathcal{E}}_{\mathrm{B}}\left(\tau \right)$ of energy stored in the B battery that can be extracted in order to perform thermodynamic work.

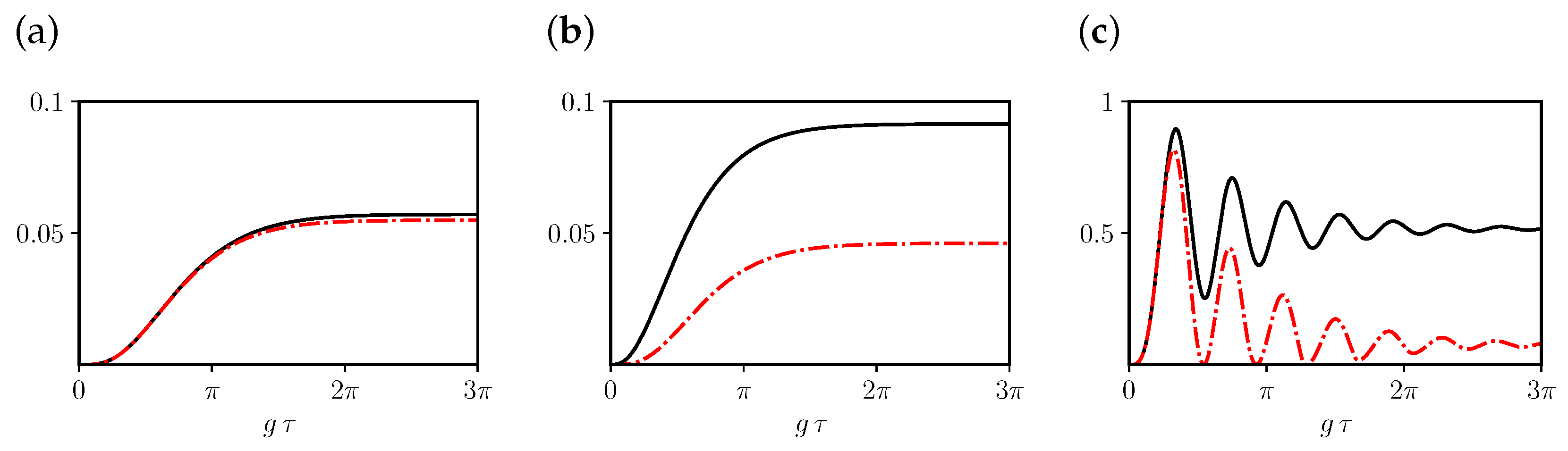
2. Results

A general framework to describe the charging process of a QB has been introduced in Refs. [5,6,7]. Here a first quantum system $\mathrm{A}$ acts as the energy “charger” that either directly injects, or facilitates the injection of energy into a second quantum system $\mathrm{B}$ that instead represents the proper battery of the model. In the simplest version of the scheme [5,6], A and B are assumed to be isolated from the outside world and characterized by local Hamiltonians ${\mathcal{H}}_{\mathrm{A}}$ and ${\mathcal{H}}_{\mathrm{B}}$ that for the sake of convenience are selected to have both zero ground-state energy. At time $t=0$ the global system starts in a pure factorized state ${|\psi \rangle }_{\mathrm{A}}\otimes {|0\rangle }_{\mathrm{B}}$, with ${|0\rangle }_{\mathrm{B}}$ being the ground state of ${\mathcal{H}}_{\mathrm{B}}$, and ${|\psi \rangle }_{\mathrm{A}}$ having mean local energy $E_{\mathrm{A}}\left(0\right):={}_{\mathrm{A}}\langle \psi |{\mathcal{H}}_{\mathrm{A}}{|\psi \rangle }_{\mathrm{A}}>0$. By switching on a coupling Hamiltonian ${\mathcal{H}}_{\mathrm{AB}}^{\left(1\right)}$ between the two systems, our aim is to transfer as much energy as possible from $\mathrm{A}$ to $\mathrm{B}$, in some finite amount of time $\tau$, the charging time of the protocol. For this purpose we write the global Hamiltonian of the model as $\mathcal{H}\left(t\right):={\mathcal{H}}_{\mathrm{A}}+{\mathcal{H}}_{\mathrm{B}}+\lambda \left(t\right){\mathcal{H}}_{\mathrm{AB}}^{\left(1\right)}$ where $\lambda \left(t\right)$ is a classical parameter that represents the external control we exert on the system, and which we assume to be given by a step function equal to 1 for $t\in [0,\tau ]$ and zero elsewhere. Accordingly, indicating with ${|\psi \left(t\right)\rangle }_{\mathrm{AB}}$ the evolved state of the system at time t, its total energy $E\left(t\right):={}_{\mathrm{AB}}\langle {\psi \left(t\right)\left|\mathcal{H}\left(t\right)\right|\psi \left(t\right)\rangle }_{\mathrm{AB}}$ is constant at all times with the exception of the switching points, $t=0$ and $t=\tau$. For the sake of simplicity we assume ${\mathcal{H}}_{\mathrm{AB}}^{\left(1\right)}$ to commute with the local terms ${\mathcal{H}}_{\mathrm{A}}+{\mathcal{H}}_{\mathrm{B}}$. Under this condition, the energy that moves from $\mathrm{A}$ to $\mathrm{B}$ can be expressed in terms of the mean local energy of the battery at the end of the protocol, i.e., the quantity [4]

$$\begin{array}{ccc}\hfill E_{\mathrm{B}}\left(\tau \right)& :=& \mathrm{tr}\left[{\mathcal{H}}_{\mathrm{B}}{\rho }_{\mathrm{B}}\left(\tau \right)\right],\hfill \end{array}$$

(1)

${\rho }_{\mathrm{B}}\left(\tau \right)$ being the reduced density matrix of the battery at time $\tau$. Even in this simplified scenario, an important question to ask is whether or not the quantity $E_{\mathrm{B}}\left(\tau \right)$ represents the full amount of energy that one could recover from the loaded battery B, without having direct access to charger A (a reasonable scenario in any relevant practical applications where charger A is not available to the end user). As explicitly discussed in Ref. [6], this is not always the case as part of $E_{\mathrm{B}}\left(\tau \right)$ can be intrinsically locked by the correlations $\mathrm{AB}$ have established during the charging process. The part of the energy of B which is free for future use is instead given by by the ergotropy [4] of the state ${\rho }_{\mathrm{B}}\left(\tau \right)$:

$${\mathcal{E}}_{\mathrm{B}}\left(\tau \right):=\mathrm{tr}\left[{\mathcal{H}}_{\mathrm{B}}{\rho }_{\mathrm{B}}\left(\tau \right)\right]-{\min }_U\mathrm{tr}\left[{\mathcal{H}}_{\mathrm{B}}U{\rho }_{\mathrm{B}}\left(\tau \right)U^{†}\right],$$

(2)

which by construction is always smaller than or equal to $E_{\mathrm{B}}\left(\tau \right)$ (the minimization being performed over the set local unitary transformations acting on B).

The situation becomes even more complicated when the charger–battery system is no longer isolated from its environment, as now, besides losses which may directly remove energy from B, the gap between ${\mathcal{E}}_{\mathrm{B}}\left({\rho }_{\mathrm{B}}\right)$ and $E_{\mathrm{B}}\left({\rho }_{\mathrm{B}}\right)$ can increase due to extra correlations the battery may have established with the AB surroundings. This scenario has been considered in Ref. [7] where the charger A is assumed to play the role of a passive transducer that simply helps the loading of energy into B from external sources described as classical coherent fields via a local Master Equation approach [8].

In the following, by considering some specific examples, we analyze the relations between ${\mathcal{E}}_{\mathrm{B}}\left({\rho }_{\mathrm{B}}\right)$ and $E_{\mathrm{B}}\left({\rho }_{\mathrm{B}}\right)$ both for the closed and for the open AB model.

3. Discussion

3.1. Closed AB Scenario

To describe the charger–battery model in the closed scenario we consider here the case where B is a two-level quantum system (qubit) while the charger A is a harmonic oscillator with frequency ${\omega }_0$ that matches the energy gap of the battery (hereafter we take $\hslash =1$). As in Ref. [5] we assume their interaction to be governed by the Jaynes–Cummings Hamiltonian [9], a paradigmatic model to describe light–matter coupling. Accordingly, we write

$$\begin{array}{c}\hfill {\mathcal{H}}_{\mathrm{A}}:={\omega }_0{a}^{†}a,{\mathcal{H}}_{\mathrm{B}}:=\frac{{\omega }_0}{2}({\sigma }_z^{\left(B\right)}+1),{\mathcal{H}}_{\mathrm{AB}}^{\left(1\right)}:=g(a^{†}{\sigma }_{-}^{\left(B\right)}+a{\sigma }_{+}^{\left(B\right)}),\end{array}$$

(3)

where $a^{†}$ (a) is the creation (destruction) bosonic operator acting on A, ${\sigma }_{-}^{\left(B\right)}$, ${\sigma }_{+}^{\left(B\right)}$, and ${\sigma }_z^{\left(B\right)}$ are, respectively, the lowering, raising and Pauli-z operators of B, and where finally g is the coupling strength parameter of the model.

Consider then first the case where initially A is described by a Fock state ${|n\rangle }_{\mathrm{A}}$ with $n=K$ photons (B being instead in its ground eigenstate of ${\mathcal{H}}_{\mathrm{B}}$). By direct integration of the equations of motion we obtain

$$\begin{array}{c}\hfill E_{\mathrm{B}}\left(\tau \right)={\omega }_0{sin}^2\left(g\sqrt{K}\tau \right),{\mathcal{E}}_{\mathrm{B}}\left(\tau \right)=\frac{{\omega }_0}{2}\left[|cos\left(2g\sqrt{K}\tau \right)|-cos\left(2g\sqrt{K}\tau \right)\right].\end{array}$$

(4)

As evident from panel (a) of Figure 1 in this case the gap between the ergotropy of B and its mean energy closes only when the charging time is an integer multiple of $\pi /\left(2g\sqrt{K}\right)$, with full loading of the battery occurring only for the odd integers. On the contrary, the system exhibits large intervals of $\tau$ where ${\mathcal{E}}_{\mathrm{B}}\left(\tau \right)$ is exactly null.

A rather different behavior is observed instead when assuming A to be initialized into a coherent state ${|\alpha \rangle }_{\mathrm{A}}=exp\left(\alpha a^{†}-{\alpha }^{*}a\right)|0\rangle$, $|0\rangle$ being the ground state of the harmonic oscillator. In this case Equations (1) and (2) yield

$$\begin{array}{c}\hfill E_{\mathrm{B}}\left(\tau \right)={\omega }_0\sum _{m=0}^{\infty }{p}_m^{\left(K\right)}{sin}^2\left(g\sqrt{m}\tau \right),{\mathcal{E}}_{\mathrm{B}}\left(\tau \right)=\frac{{\omega }_0}{2}\left(\sqrt{r_z^2\left(\tau \right)+r_y^2\left(\tau \right)}+r_z\left(\tau \right)\right),\end{array}$$

(5)

where for m integer $p_m^{\left(K\right)}:=K{e}^{-K}/m!$, $r_z\left(\tau \right):=-{\sum }_m{p}_m^{\left(K\right)}{cos}^2\left(2g\sqrt{m}\tau \right)$, $r_y\left(\tau \right):={\sum }_m{K}^{\frac{2m+1}{2}}{e}^{-K}/\sqrt{m!(m+1)!}2cos\left(g\sqrt{m}\tau \right)sin\left(g\sqrt{m+1}\tau \right)$, and where $K={\left|\alpha \right|}^2$ gauges once more the input mean energy of A via the identity $E_A\left(0\right)={\omega }_{0}K$. As shown in the panels (b,c) of Figure 1, in this case ${\mathcal{E}}_{\mathrm{B}}\left(\tau \right)$ becomes zero only for isolated values of $\tau$, a property which ultimately can be related to the fact that coherent states are optimal in minimizing the amount of correlations produced during the dynamics [6]. Furthermore, as expected from semiclassical considerations, in the high mean input energy limit (i.e., $K\to \infty$), the ergotropy ${\mathcal{E}}_{\mathrm{B}}\left(\tau \right)$ approaches asymptomatically $E_{\mathrm{B}}\left(\tau \right)$, (see also panel (c)). In this regime it also occurs that the maximum value of $E_{\mathrm{B}}\left(\tau \right)$ can reach the full charging threshold ${\omega }_0$ for $\tau =\pi /\left(2g\sqrt{K}\right)$.

3.2. Open AB Scenario

As anticipated in the introduction in the open AB scenario [7], the charger acts merely as a mediator between B and the external world whose contribution is represented via a local Master Equation [8]. Specifically, in this case we describe the evolution of the joint density matrix ${\rho }_{\mathrm{AB}}\left(t\right)$ of AB in terms of the following differential equation

$${\dot{\rho }}_{\mathrm{AB}}\left(t\right)=-i\left[{\mathcal{H}}_{\mathrm{A}}+{\mathcal{H}}_{\mathrm{B}},{\rho }_{\mathrm{AB}}\left(t\right)\right]+\lambda \left(t\right){\mathcal{L}}_{\mathrm{AB}}\left(t\right)\left[{\rho }_{\mathrm{AB}}\left(t\right)\right],$$

(6)

where, as in the previous section ${\mathcal{H}}_{\mathrm{A}}$ and ${\mathcal{H}}_{\mathrm{B}}$ represent the local Hamiltonians of A and B and $\lambda \left(t\right)$ is the step-like control function. The term ${\mathcal{L}}_{\mathrm{AB}}\left(t\right)$ on the contrary is a (possibly time dependent) Gorini–Kossakolski–Sudarshan–Lindblad (GKSL) super-operator [10,11]

$${\mathcal{L}}_{\mathrm{AB}}\left(t\right)[\cdots ]:=-i\left[\Delta {\mathcal{H}}_{\mathrm{A}}\left(t\right)+{\mathcal{H}}_{\mathrm{AB}}^{\left(1\right)},\cdots \right]+{\mathcal{D}}_{\mathrm{A}}^{\left(\mathrm{T}\right)}[\cdots ],$$

(7)

which includes a temperature dependent dissipative contribution ${\mathcal{D}}_{\mathrm{A}}^{\left(\mathrm{T}\right)}$ and a Hamiltonian term which accounts both for the AB interactions ${\mathcal{H}}_{\mathrm{AB}}^{\left(1\right)}$ and for the classical driving $\Delta {\mathcal{H}}_{\mathrm{A}}\left(t\right)$ of the charger. Assuming then the AB system to be initialized into the ground state configuration ${\rho }_{AB}\left(0\right)=|0\rangle \langle 0|\otimes |0\rangle {\langle 0|}_{\mathrm{AB}}$ of their respective Hamiltonians, one can study the charging of B through the mediation of A by focusing once more on the quantities (1) and (2). In Figure 2 we report the behaviors of these quantities obtained for the case where as in Section 3.1, B is a two level system and A is a harmonic oscillator of frequency ${\omega }_0$ resonant with the energy gap of the battery (different configurations are considered in Ref. [7]): accordingly, we now take $\Delta {\mathcal{H}}_{\mathrm{A}}\left(t\right):=F(e^{-i{\omega }_{0}t}{a}^{†}+h.c.)$, as a driving term for A, and

$${\mathcal{D}}_{\mathrm{A}}^{\left(\mathrm{T}\right)}[\cdots ]:=\gamma \left(N_b\left(T\right)+1\right){\mathcal{D}}_a[\cdots ]+\gamma N_b\left(T\right){\mathcal{D}}_{a^{†}}[\cdots ],$$

(8)

with $N_b\left(T\right)$ being the Bose occupation number $N_b\left(T\right):=\frac{1}{e^{{\omega }_0/\left(K_{b}T\right)}-1}$ of the thermal bath coupled to A, $\gamma$ being a constant characterizing the dissipation rate, and ${\mathcal{D}}_{\theta }[\cdots ]:=\theta [\cdots ]{\theta }^{†}-\frac{1}{2}\{{\theta }^{†}\theta ,\cdots \}.$ As evident from a comparison between panels (a) and (b) of the figure, increasing the bath temperature, while increasing the mean energy on B, typically tends to deteriorate the ergotropy level in the system (exceptions to this however have been reported in Ref. [7]). Panel (c) of Figure 2 instead shows that for large F and low T, the behavior of $E_{\mathrm{B}}\left(\tau \right)$ and ${\mathcal{E}}_{\mathrm{B}}\left(\tau \right)$ keep some resemblance with the functional dependence observed in the semiclassical limit of the closed case scenario, i.e., panel (c) of Figure 1.