Entanglement Assisted Transport of Two Walkers in Noisy Quantum Networks ^†

Abstract

Understanding the transport mechanisms and properties of complex networks is fundamental for the comprehension of a vast class of phenomena, from state transfer on a spin network to light-harvesting in photosynthetic complexes. It has been theoretically and experimentally demonstrated that noise can enhance transport when the system parameters are properly tuned, an effect known as noise-assisted transport (NAT). In this work we investigate the role of initial entanglement in the transfer efficiency of two walkers in a noisy network. By using the formalism of quantum walks, we define a range of small dephasing noise where initial site-entanglement provides transport enhancement and outperforms the NAT effect. Furthermore, we show two specific scenarios where entanglement-assisted transport can open faster channels for slow walkers and avoid a broken link in a communication line. These findings may be of potential interest for quantum technologies.

1. Introduction

Understanding transport mechanisms across a noisy quantum network is crucial to the development of quantum information and communication technologies [1]. Quantum walk dynamics on networks represents an extensively used tool to model quantum channels of any topology and to investigate optimal signal propagation in a controllable environment [2]. As recently demonstrated by quantum network theory applied to biological photosynthetic complexes [3], a proper tuning of environmental noise in a partially incoherent dynamics can lead to energy transport enhancement and explain surprisingly high light-harvesting efficiencies. This phenomenon of noise-assisted transport (NAT) has been experimentally proved in several photonic platforms where a coherent state of light is used to simulate a single quantum walker in a noisy network [4,5]. However, in this scenario quantum interference can be indeed classically simulated and a coherent source experiment reproduces the same statistics of a single-photon experiment repeated several times [6].

Here, since the occurrence of quantum coherence itself is not sufficient to prove the non-classicality of a phenomenon [7], we want to analyze a truly quantum behaviour entailing the presence of more than one walker, thus making the complexity of multi-particle quantum walks emerge [8]. In this framework we are interested in the role of entanglement [9] as the quantum feature with an essentially non-classical statistics. We will use continuous-time quantum walks of two walkers in noisy networks to discuss if site-entanglement of the initial state can assist energy transport. We will compare the dynamics for different externally tunable parameters, such as initial two walkers state and their level of entanglement. Our analysis will include also the effect of dephasing noise. We will show numerical solutions for three different network designs that can be considered representative of common physical situations. These results prove evidence of entanglement-assisted transport (EAT) and we believe this exploratory work might stimulate further investigations and experimental implementations.

2. Results

2.1. Theoretical Model

Each site of the considered networks is represented by a two-state system (qubit) as in ref. [3]. The effective N-qubits Hamiltonian (where N is the total number of sites) describes the coherent dynamics and is

$$\widehat{\mathcal{H}}=\sum _i\hslash {\omega }_i{\widehat{a}}_i^{†}{\widehat{a}}_i+\sum _{i,j}\hslash g_{ij}({\widehat{a}}_i^{†}{\widehat{a}}_j+{\widehat{a}}_j^{†}{\widehat{a}}_i),$$

(1)

with ${\widehat{a}}_i$ and ${\widehat{a}}_i^{†}$ being the usual bosonic field operators, annihilating and creating a photon in site i, $\hslash {\omega }_i$ the site resonance and $g_{ij}$ the coupling rates between connected sites. Lindblad operators ${\mathcal{L}}_{deph}$ and ${\mathcal{L}}_{sink}$ model respectively pure dephasing noise and the irreversible dissipation throughout a sink-site s for the measurement of transfer efficiency, namely

$${\mathcal{L}}_{deph}\left(\widehat{\rho }\right)=\sum _i{\gamma }_i\left[-\left\{{\widehat{a}}_i^{†}{\widehat{a}}_i,\widehat{\rho }\right\}+2{\widehat{a}}_i^{†}{\widehat{a}}_i\widehat{\rho }{\widehat{a}}_i^{†}{\widehat{a}}_i\right];$$

(2)

$${\mathcal{L}}_{sink}\left(\widehat{\rho }\right)={\Gamma }_{sink}\left[2{\widehat{a}}_s\widehat{\rho }{\widehat{a}}_s^{†}-\left\{{\widehat{a}}_s^{†}{\widehat{a}}_s,\widehat{\rho }\right\}\right],$$

(3)

with $\widehat{\rho }$ being the density matrix operator describing the walkers state, ${\gamma }_i$ the dephasing rates at site i, and ${\Gamma }_{sink}$ the dissipative rate throughout the sink, respectively. The transport dynamics can be described by the time evolution of the state via the following differential Lindblad master equation

$$(d/dt)\widehat{\rho }\left(t\right)=-(i/\hslash )[\widehat{\mathcal{H}},\widehat{\rho }\left(t\right)]+{\mathcal{L}}_{deph}\left(\widehat{\rho }\left(t\right)\right)+{\mathcal{L}}_{sink}\left(\widehat{\rho }\left(t\right)\right).$$

(4)

The initial condition for the density matrix $\widehat{\rho }\left(t_0\right)$ is set by the initial preparation of the two-walker state in the N-sites network, which will generally be

$$|\psi \rangle =(\alpha |1_j{1}_k{0}_{l\ne j,k}\rangle +\beta |1_m{1}_n{0}_{l\ne m,n}\rangle )/\sqrt{2};j,k,m,n,l\in [1,\dots ,N]$$

(5)

where $1_i$ ($0_i$) in the ket-notation represents the excited (ground) state in site i. In Equation (5), $\alpha$ and $\beta$ satisfy the state vector normalization condition and define the level of entanglement between the excited sites j and k, with the control sites m and n. In this work, we will label the initial configuration of excited and control sites as $(j,k,m,n)$. We will consider $\alpha =\beta =1$ for an initial bipartite maximally entangled state, $\alpha =2$, $\beta =0$ for a pure state of independent walkers in sites i and j, and an intermediate case $\alpha =\sqrt{3/2}$, $\beta =1/\sqrt{2}$. Correspondingly, bipartite entanglement holds $E\left(t_0\right)=1$, $E\left(t_0\right)=0$, $E\left(t_0\right)=0.9$, where we quantify entanglement across a bipartition $A|B$ by using the logarithmic negativity

$$E\left(A\right|B)=lo{g}_2\parallel {\rho }^{{\Gamma }_A}\parallel ,$$

(6)

with ${\Gamma }_A$ being the partial transpose operation with respect to the subsystem A and $\parallel ·\parallel$ the trace norm.

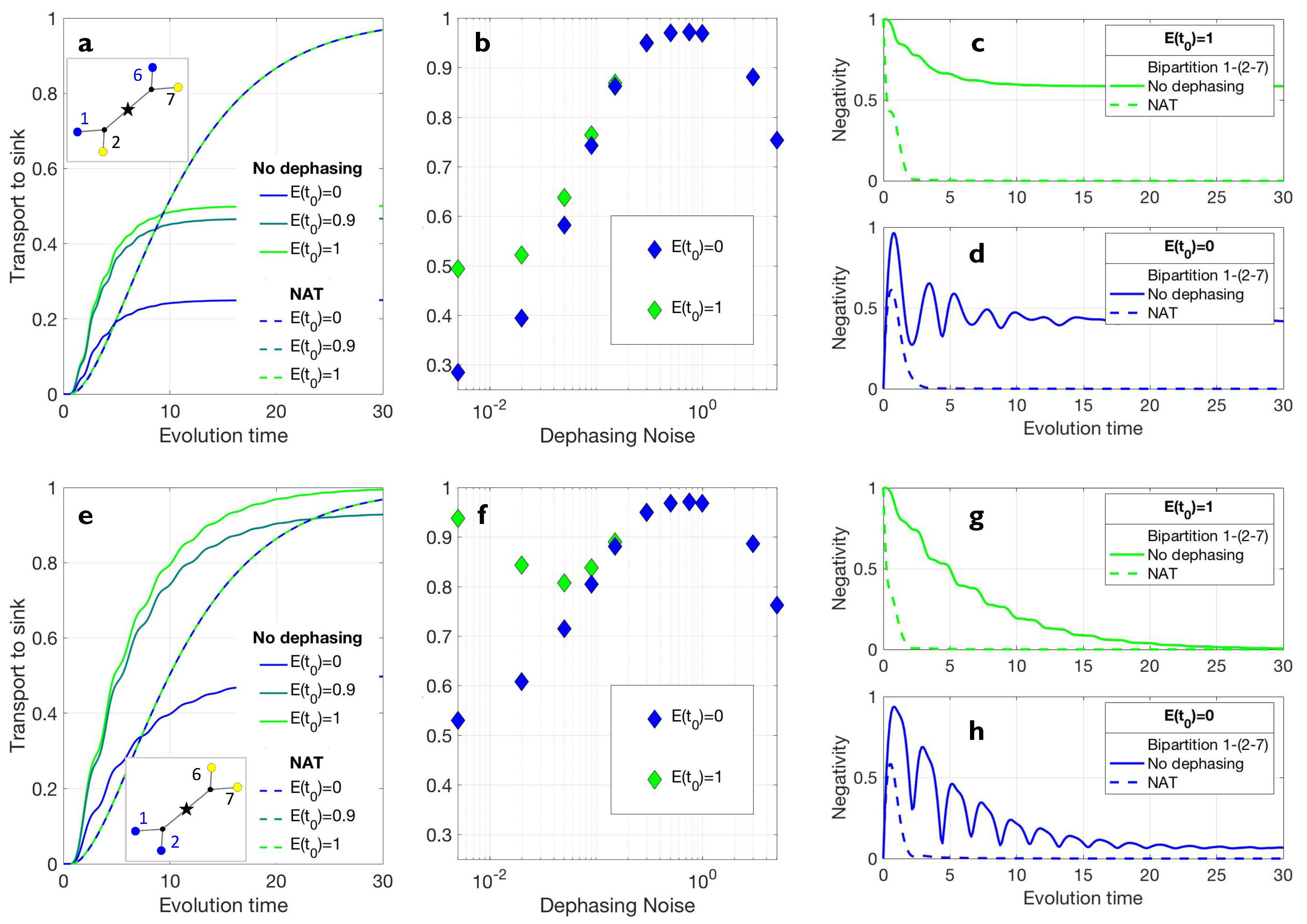
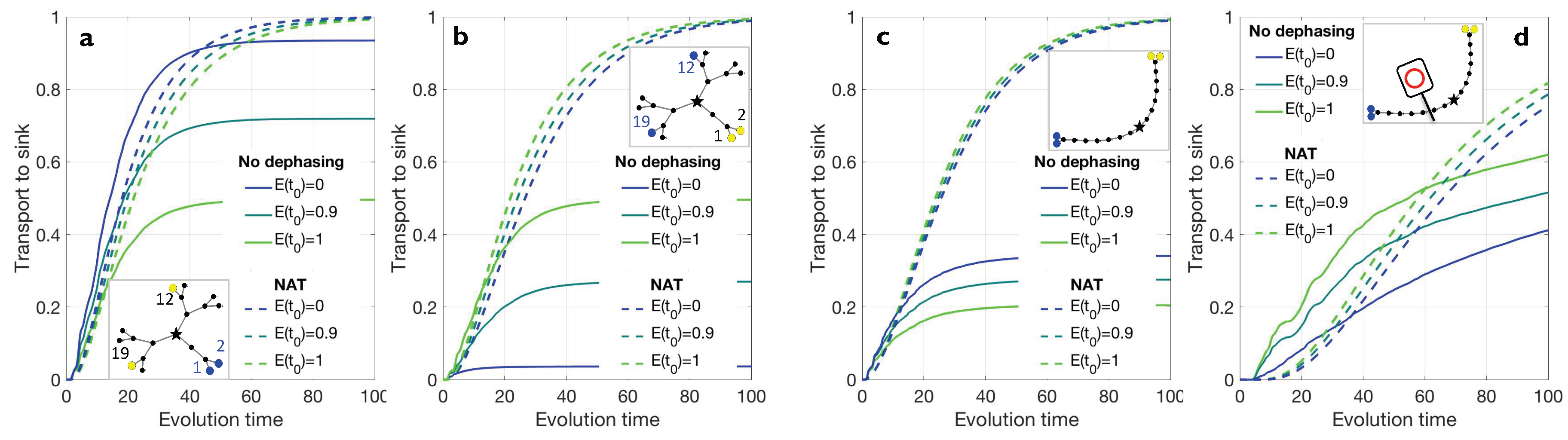
2.2. Numerical Simulations

For each considered network we use fixed ${\Gamma }_{sink}$, $\hslash =1$, ${\omega }_i=1$, ${\gamma }_i=1$, and in general $g_{ij}=1$$\forall i,j$. We show in the top and bottom row of Figure 1 the solutions for two different initial two-walker states in the simplest network design, with the excitation sites j, k (blue), and the control sites m, n (yellow) not directly connected to the sink (as in the respective insets on the left), i. e. in the initial configurations $(j,k,m,n)=(1,6,2,7)$ and $(j,k,m,n)=(1,2,6,7)$.

In Figure 1a,e we compare a pure coherent dynamics without dephasing (solid line) with the optimal NAT dynamics (dashed line). While the NAT dynamics is not affected by the initial presence of entanglement (colours overlap), at zero dephasing having $E\left(t_0\right)=1$ is twice more efficient than $E\left(t_0\right)=0$ at stationary condition, for both configurations. As first interesting result, we can define the range of dephasing rates for which entanglement-assisted transport is robust in Figure 1b,f, where we report on the transport efficiency at stationary conditions. For high dephasing rates the decoherence rapidly suppresses initial entanglement and noise-assisted transport prevails. In Figure 1c,d,g,h we show the evolution of entanglement during the dynamics. Of course, entanglement is independently generated also when $E\left(t_0\right)=0$. For all cases, dashed lines show the fast suppression in presence of noise. By considering the coherent behaviour at stationary conditions, we note, as second interesting result, that bipartite entanglement for the initial configuration $(j,k,m,n)=(1,6,2,7)$ (top figures) sets at a non-zero value beside the presence of a dissipative sink. This behaviour is the evidence of the action of dark subspaces[3,10] of the Hamiltonian that block transportation. Setting the initial state to a different configuration $(j,k,m,n)=(1,2,6,7)$ (bottom figures) allows to properly avoid this subspace and thus to have optimal transport efficiency in the coherent dynamics, outperforming also the optimal NAT efficiency (Figure 1e).

In this second part we display two scenarios where entanglement can be properly exploited to help lost walkers in a multi-choice network, or to bypass a damaged channel in a linear network.

We summarize the third interesting result with the transport efficiency plots in Figure 2. For the first case we use a dendrimer network where sites $1,2$ are directly connected to the sink while $12,19$ are separated from it by a double choice path. Figure 2a,b refer to the two preparation states $(j,k,m,n)=(1,2,12,19)$ and $(j,k,m,n)=(12,19,1,2)$ (as in the insets). Considering the coherent dynamics, it is evident how quantum correlations are disadvantageous in the first solution while they benefit transport efficiency in the latter: initial entanglement with control sites that are directly connected to the sink can open convenient short-cut channels for lost walkers. The same behaviour, though attenuated, is preserved in the optimal NAT dynamics. Regarding the second investigation, we use as shown in Figure 2c, a continuum communication line with four input ports at the ends, and in Figure 2d, we damage an internal channel between the excitation sites and the sink, leaving the communication between sink and control sites undamaged. We can observe in the coherent dynamics in the case of the continuum network that entanglement is counter-productive, but as soon as the symmetry is broken and the coupling to one channel is lowered ($g=0.25$ in Equation (1)) initial entanglement with the control sites is a valid tool to bypass the obstacle.

3. Conclusions

In this manuscript we have studied the role of initial entanglement in the transport efficiency of two walkers in a quantum network. We have used the simplest topology of four preparation sites not directly connected to the sink to show evidence of entanglement-assisted transport and to identify the range where it is robust against dephasing noise. For higher dephasing rates the effect vanishes and noise-assisted transport prevails. Due to the small network dimension, we have shown that the site-configuration of the initial state is crucial to avoid dark states in the Hamiltonian and that EAT outperforms NAT in a coherent dynamics. Finally, we have displayed two physical scenarios where initial entanglement can be exploited to enhance transport in slower channels in a dendrimer network and to reduce the effect of a damaged link in a communication line, providing new insights for future application in quantum communication technologies and energy transport.