Graphene Josephson Junction Quantum Circuits for Noise Detection †
Abstract
:1. Introduction
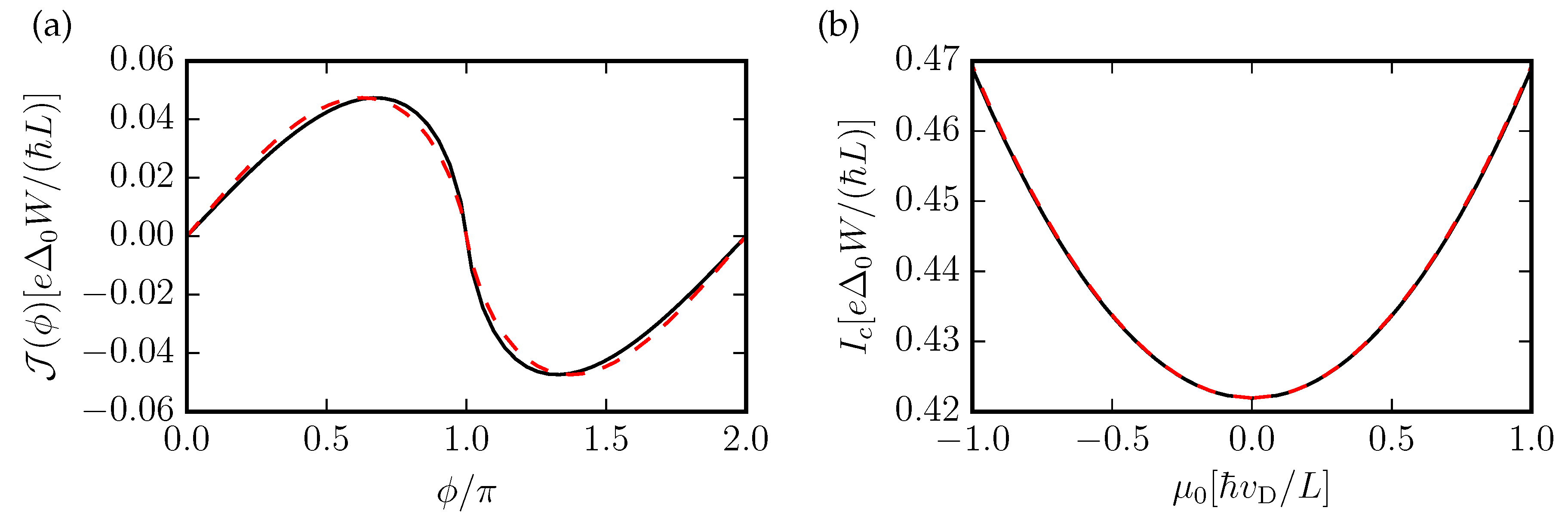
2. Current-Phase Relation for Finite Doping at
3. GJJ Phase Qubit for Noise Sensing
4. Conclusions
References
- Wang, L.; Meric, I.; Huang, P.Y.; Gao, Q.; Gao, Y.; Tran, H.; Taniguchi, T.; Watanabe, K.; Campos, L.M.; Muller, D.A.; Guo, J.; Kim, P.; Hone, J.; Shepard, K.L.; Dean, C.R. One-Dimensional Electrical Contact to a Two-Dimensional Material. Science 2013, 342, 614. [Google Scholar] [CrossRef]
- Dean, C.R.; Young, A.F.; Meric, I.; Lee, C.; Wang, L.; Sorgenfrei, S.; Watanabe, K.; Taniguchi, T.; Kim, P.; Shepard, K.L.; Hone, J. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotech. 2010, 5, 722–726. [Google Scholar] [CrossRef]
- Mayorov, A.S.; Gorbachev, R.V.; Morozov, S.V.; Britnell, L.; Jalil, R.; Ponomarenko, L.A.; Blake, P.; Novoselov, K.S.; Watanabe, K.; Taniguchi, T.; Geim, A.K. Micrometer-Scale Ballistic Transport in Encapsulated Graphene at Room Temperature. Nano Lett. 2011, 11, 2396–2399. [Google Scholar] [CrossRef] [PubMed]
- Shalom, M.B.; Zhu, M.J.; Fal’ko, V.I.; Mishchenko, A.; Kretinin, A.V.; Novoselov, K.S.; Woods, C.R.; Watanabe, K.; Taniguchi, T.; Geim, A.K.; Prance, J.R. Quantum oscillations of the critical current and high-field superconducting proximity in ballistic graphene. Nature Phys. 2015, 12, 318–322. [Google Scholar] [CrossRef]
- Calado, V.E.; Goswami, S.; Nanda, G.; Diez, M.; Akhmerov, A.R.; Watanabe, K.; Taniguchi, T.; Klapwijk, T.M.; Vandersypen, L.M.K. Ballistic Josephson junctions in edge-contacted graphene. Nat. Nano 2015, 10, 761. [Google Scholar] [CrossRef]
- English, C.D.; Hamilton, D.R.; Chialvo, C.; Moraru, I.C.; Mason, N.; van Harlingen, D.J. Observation of nonsinusoidal current-phase relation in graphene Josephson junctions. Phys. Rev. B 2016, 94, 115435. [Google Scholar] [CrossRef]
- Borzenets, I.V.; Amet, F.; Ke, C.T.; Draelos, A.W.; Wei, M.T.; Seredinski, A.; Watanabe, K.; Taniguchi, T.; Bomze, Y.; Yamamoto, M.; et al. Ballistic Graphene Josephson Junctions from the Short to the Long Junction Regimes. Phys. Rev. Lett. 2016, 117, 237002. [Google Scholar] [CrossRef]
- Nanda, G.; Aguilera-Servin, J.L.; Rakyta, P.; Kormanyos, A.; Kleiner, R.; Koelle, D.; Watanabe, K.; Taniguchi, T.; Vandersypen, L.M.K.; Goswami, S. Current-Phase Relation of Ballistic Graphene Josephson Junctions. Nano Lett. 2017, 17, 3396–3401. [Google Scholar] [CrossRef]
- Park, J.; Lee, J.H.; Lee, G.-H.; Takane, Y.; Imura, K.-I.; Taniguchi, T.; Watanabe, K.; Lee, H.-J. Short Ballistic Josephson Coupling in Planar Graphene Junctions with Inhomogeneous Carrier Doping. Phys. Rev. Lett. 2018, 120, 077701. [Google Scholar] [CrossRef]
- Titov, M.; Beenakker, C.W.J. Josephson effect in ballistic graphene. Phys. Rev. B 2006, 74, 041401. [Google Scholar] [CrossRef]
- Schmidt, F.E.; Jenkins, M.D.; Watanabe, K.; Taniguchi, T.; Steele, G.A. A ballistic graphene superconducting microwave circuit. Nat. Commu. 2018, 9, 4069. [Google Scholar] [CrossRef]
- Kroll, J.G.; Schmidt, F.E.; Jenkins, M.D.; Watanabe, K.; Taniguchi, T.; Steele, G.A. Magnetic field compatible circuit quantum electrodynamics with graphene Josephson junctions. Nat. Commu. 2018, 9, 4615. [Google Scholar] [CrossRef]
- Zwick, A.; Alvarez, G.A.; Kurizki, G. Maximizing Information on the Environment by Dynamically Controlled Qubit Probes. Phys. Rev. Appl. 2016, 5, 014007. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Paladino, E.; Galperin, Y.M.; Falci, G.; Altshuler, B.L. 1/f noise: Implications for solid-state quantum information. Rev. Mod. Phys. 2014, 86, 361. [Google Scholar] [CrossRef]
- Martinis, J.M.; Nam, S.; Aumentado, J.; Urbina, C. Rabi Oscillations in a Large Josephson-Junction Qubit. Phys. Rev. Lett. 2002, 89, 117901. [Google Scholar] [CrossRef]
- Martinis, J.M.; Nam, S.; Aumentado, J.; Lang, K.M.; Urbina, C. Decoherence of a superconducting qubit due to bias noise. Phys. Rev.B 2003, 67, 094510. [Google Scholar] [CrossRef]
- Devoret, M.H.; Martinis, J.M.; Clarke, J. Measurements of Macroscopic Quantum Tunneling out of the Zero-Voltage State of a Current-Biased Josephson Junction. Phys. Rev. Lett. 1985, 55, 1908. [Google Scholar] [CrossRef]
- Paladino, E.; D’arrigo, A.; Mastellone, A.; Falci, G. Decoherence times of universal two-qubit gates in the presence of broad-band noise. New J. Phys. 2011, 13, 09037. [Google Scholar] [CrossRef]
- Faoro, L.; Viola, L. Dynamical suppression of 1/f noise processes in qubit systems. Phys. Rev. Lett. 2004, 92, 117905. [Google Scholar] [CrossRef]
- Falci, G.; D’Arrigo, A.; Mastellone, A.; Paladino, E. Dynamical suppression of telegraph and 1/f noise due to quantum bistable fluctuators. Phys. Rev. A 2004, 70, 040101. [Google Scholar] [CrossRef]
- Cywinski, L.; Lutchyn, R.M.; Nave, C.P.; Sarma, S.D. How to enhance dephasing time in superconducting qubits. Phys. Rev. B 2008, 77, 174509. [Google Scholar] [CrossRef]
- D’Arrigo, A.; Falci, G.; Paladino, E. Quantum Zeno and anti-Zeno effect on a two-qubit gate by dynamical decoupling. EPJ-ST 2019, 227, 2189. [Google Scholar] [CrossRef]
- D’Arrigo, A.; Falci, G.; Paladino, E. High-fidelity two-qubit gates via dynamical decoupling of local 1/f noise at the optimal point. Phys. Rev. A 2016, 94, 022303. [Google Scholar] [CrossRef]
- Biercuk, M.J.; Doherty, A.C.; Uys, H. Dynamical decoupling sequence construction as a filter-design problem. J. Phys. B: At. Mol. Opt. Phys. 2011, 44, 154002. [Google Scholar] [CrossRef]
- Bylander, J.; Gustavsson, S.; Yan, F.; Yoshihara, F.; Harrabi, K.; Fitch, G.; Cory, D.G.; Nakamura, Y.; Tsai, J.-S.; Oliver, W.D. Noise spectroscopy through dynamical decoupling with a superconducting flux qubit. Nat. Phys. 2011, 7, 565. [Google Scholar] [CrossRef]
- Yuge, T.; Sasaki, S.; Hirayama, Y. Measurement of the noise spectrum using a multiple-pulse sequence. Phys. Rev. Lett. 2011, 107, 170504. [Google Scholar] [CrossRef] [PubMed]
- Yan, F.; Bylander, F.; Gustavsson, S.; Yoshihara, F.; Harrabi, K.; Cory, D.G.; Orlando, T.P.; Nakamura, Y.; Tsai, J.-S.; Oliver, W.D. Spectroscopy of low-frequency noise and its temperature dependence in a superconducting qubit. Phys. Rev. B 2012, 85, 174521. [Google Scholar] [CrossRef]
- Palma, G.; Suominen, K.; Ekert, A. Quantum computers and dissipation. Proc. R. Soc. A 1996, 452, 567. [Google Scholar] [CrossRef]
- Kofman, A.G.; Kurizki, G. Universal Dynamical Control of Quantum Mechanical Decay: Modulation of the Coupling to the Continuum. Phys. Rev. Lett. 2001, 87, 270405. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pellegrino, F.M.D.; Falci, G.; Paladino, E. Graphene Josephson Junction Quantum Circuits for Noise Detection. Proceedings 2019, 12, 33. https://doi.org/10.3390/proceedings2019012033
Pellegrino FMD, Falci G, Paladino E. Graphene Josephson Junction Quantum Circuits for Noise Detection. Proceedings. 2019; 12(1):33. https://doi.org/10.3390/proceedings2019012033
Chicago/Turabian StylePellegrino, Francesco Maria Dimitri, Giuseppe Falci, and Elisabetta Paladino. 2019. "Graphene Josephson Junction Quantum Circuits for Noise Detection" Proceedings 12, no. 1: 33. https://doi.org/10.3390/proceedings2019012033
APA StylePellegrino, F. M. D., Falci, G., & Paladino, E. (2019). Graphene Josephson Junction Quantum Circuits for Noise Detection. Proceedings, 12(1), 33. https://doi.org/10.3390/proceedings2019012033





