Experimental Connection between the Instrumental and Bell Inequalities †
Abstract
:1. Introduction
2. Results
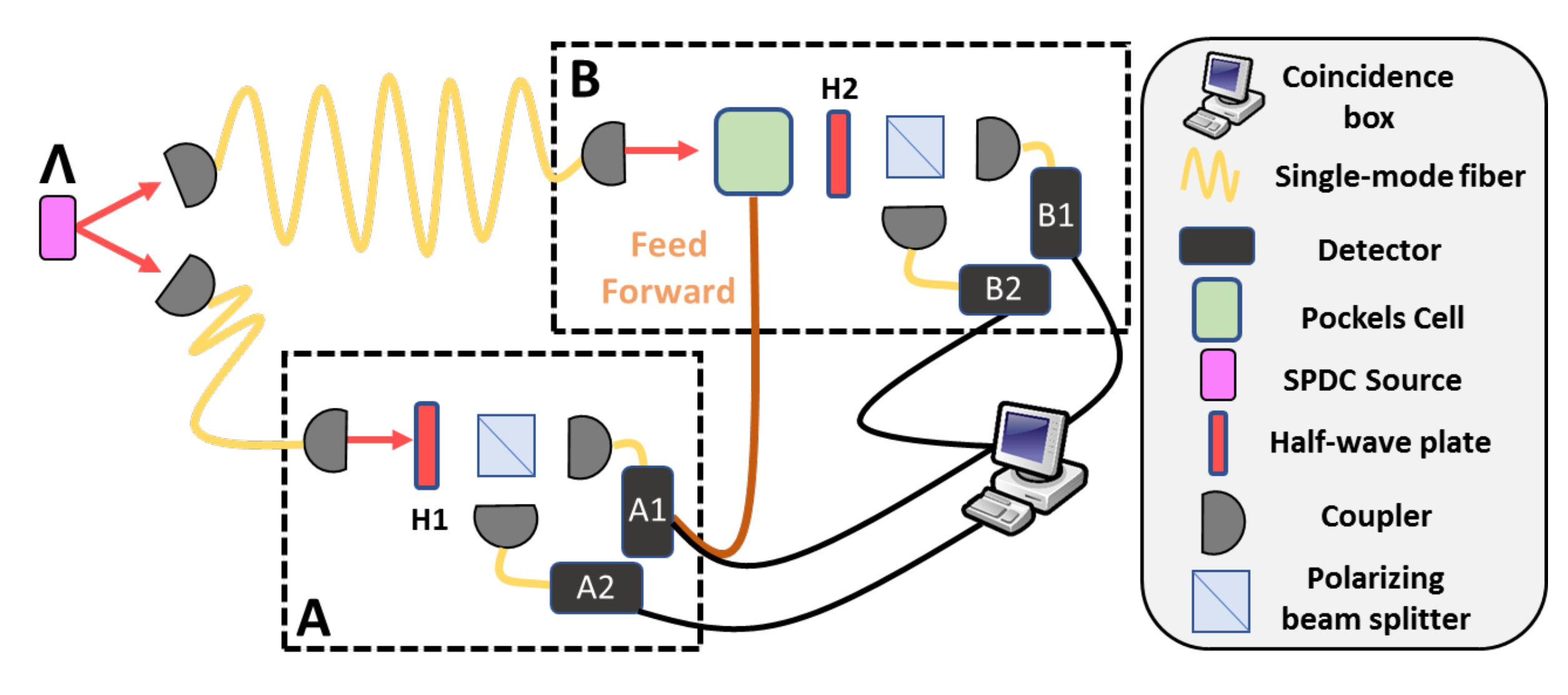
2.1. Active Feed-Forward of Information
2.2. Post-Selection Scenario
2.2.1. Relation between Bonet and CHSH Inequality Violation
2.2.2. CHSH Violation within an Instrumental Process
3. Discussion
4. Materials and Methods
Acknowledgments
Conflicts of Interest
Abbreviations
| CHSH | Clauser-Horne-Shimony-Holt inequality |
| DAG | Directed Acyclic Graph |
| HWP | Half-wave plate |
| PBS | Polarizing Beam Splitter |
| BBO | Beta-Barium Borate |
| SPDC | Spontaneous Parametric Down-Conversion |
References
- Pearl, J. On the testability of causal models with latent and instrumental variables. In Proceedings of the 11th conference on Uncertainty in artificial intelligence (UAI ’95), Montreal, QC, Canada, 18–20 August 1995; pp. 435–443. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning and Inference, 2nd ed.; Cambridge University Press: New York, NY, USA, 2009; ISBN 978-0521895606. [Google Scholar]
- Bonet, B. Instrumentality Tests Revisited. Proceedings 17th Conference Uncertainty in Artificial Intelligence, Seattle, WA, USA, 2–5 August 2001; pp. 48–55. [Google Scholar]
- Popescu, S.; Rohrlich, D. Quantum Nonlocality as an axiom. Found. Phys. 1994, 24, 379–385. [Google Scholar] [CrossRef]
- Leifer, M.S.; Spekkens, R.W. Towards a formu- lation of quantum theory as a causally neutral theory of bayesian inference. Phys. Rev. A 2013, 88, 052130. [Google Scholar] [CrossRef]
- Fritz, T. Beyond bell’s theorem ii: Scenarios with arbitrary causal structure. Commun. Math. Phys. 2016, 341, 391–434. [Google Scholar] [CrossRef]
- Procopio, L.M.; Moqanaki, A.; Araújo, M.; Costa, F.; Calafell, I.A.; Dowd, E.G.; Hamel, D.R.; Rozema, L.A.; Brukner, C.; Walther, P. Experimental superposition of orders of quantum gates. Nat. Comm. 2015, 6, 7913. [Google Scholar] [CrossRef] [PubMed]
- Rubino, G.; Rozema, L.A.; Feix, A.; Araújo, M.; Uner, J.M.Z.; Procopio, L.M.; Brukner, C.; Walther, P. Experimental verification of an indefinite causal order. Sci. Adv. 2017, 3, e1602589. [Google Scholar] [CrossRef]
- Henson, J.; Lal, R.; Pusey, M.F. Theory-independent limits on correlations from generalized bayesian net- works. New J. Phys. 2014, 16, 113043. [Google Scholar] [CrossRef]
- Chaves, R.; Majenz, C.; Gross, D. Information-theoretic implications of quantum causal structures. Nat. Commun. 2015, 6, 5766. [Google Scholar] [CrossRef]
- Costa, F.; Shrapnel, S. Quantum causal modelling. New J. Phys. 2016, 18, 063032. [Google Scholar] [CrossRef]
- Allen, J.-M.A.; Barrett, J.; Horsman, D.C.; Lee, C.M.; Spekkens, R.W. Quantum common causes and quantum causal models. Phys. Rev. X 2016, 7, 031021. [Google Scholar] [CrossRef]
- Pienaar, J.; Brukner, C. A graph-separation theorem for quantum causal models. New J. Physics 2015, 17, 073020. [Google Scholar] [CrossRef]
- Bell, J. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fizika 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef]
- Cirel’son, B.S. Quantum generalizations of Bell’s inequality. Lett. Math. Phys. 1980, 4, 83. [Google Scholar] [CrossRef]
- Carvacho, G.; Andreoli, F.; Santodonato, L.; Bentivegna, M.; Chaves, R.; Sciarrino, F. Experimental violation of local causality in a quantum network. Nat. Comm. 2017, 8, 14775. [Google Scholar] [CrossRef]
- Andreoli, F.; Carvacho, G.; Santodonato, L.; Bentivegna, M.; Chaves, R.; Sciarrino, F. Experimental bilocality violation without shared reference frames. Phys. Rev. A 2015, 95, 062315. [Google Scholar] [CrossRef]
- Saunders, D.J.; Bennet, A.J.; Branciard, C.; Pryde, G.J. Experimental demonstration of nonbilocal quantum correlations. Sci. Adv. 2017, 3, e1602743. [Google Scholar] [CrossRef]
- Ringbauer, M.; Chaves, R. Probing the non- classicality of temporal correlation. Quantum 2017, 1, 35. [Google Scholar] [CrossRef]
- Ringbauer, M.; Giarmatzi, C.; Chaves, R.; Costa, F.; White, A.G.; Fedrizzi, A. Experimental test of nonlocal causality. Sci. Adv. 2016, 2, e1600162. [Google Scholar] [CrossRef]
- Chaves, R. Polynomial bell inequalities. Phys. Rev. Lett. 2016, 116, 010402. [Google Scholar] [CrossRef]
- Lee, C.M.; Horan, M.J. Towards Device-Independent Information Processing on General Quantum Networks. Phys. Rev. Lett. 2018, 120, 020504. [Google Scholar] [CrossRef]
- Chaves, R.; Carvacho, G.; Agresti, I.; di Giulio, V.; Aolita, L.; Giacomini, S.; Sciarrino, F. Quantum violation of an instrumental test. Nat. Phys. 2018, 14, 291–296. [Google Scholar] [CrossRef]
- Van Himbeeck, T.; Brask, J.B.; Pironio, S.; Ramanathan, R.; Sainz, A.B.; Wolfe, E. Quantum violations in the instrumental scenario and their relations to the Bell scenario. arXiv 2018, arXiv:1804.04119. [Google Scholar] [CrossRef]
- Sciarrino, F.; Ricci, M.; de Martini, F.; Filip, R.; Mista, L. Realization of a minimal disturbance quantum measurement. Phys. Rev. Lett. 2006, 96, 020408. [Google Scholar] [CrossRef] [PubMed]
- Giacomini, S.; Sciarrino, F.; Lombardi, E.; de Martini, F. Active teleportation of a quantum bit. Phys. Rev. A 2002, 66, 030302. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agresti, I.; Carvacho, G.; Poderini, D.; Aolita, L.; Chaves, R.; Sciarrino, F. Experimental Connection between the Instrumental and Bell Inequalities. Proceedings 2019, 12, 27. https://doi.org/10.3390/proceedings2019012027
Agresti I, Carvacho G, Poderini D, Aolita L, Chaves R, Sciarrino F. Experimental Connection between the Instrumental and Bell Inequalities. Proceedings. 2019; 12(1):27. https://doi.org/10.3390/proceedings2019012027
Chicago/Turabian StyleAgresti, Iris, Gonzalo Carvacho, Davide Poderini, Leandro Aolita, Rafael Chaves, and Fabio Sciarrino. 2019. "Experimental Connection between the Instrumental and Bell Inequalities" Proceedings 12, no. 1: 27. https://doi.org/10.3390/proceedings2019012027
APA StyleAgresti, I., Carvacho, G., Poderini, D., Aolita, L., Chaves, R., & Sciarrino, F. (2019). Experimental Connection between the Instrumental and Bell Inequalities. Proceedings, 12(1), 27. https://doi.org/10.3390/proceedings2019012027





