Abstract
The observation of genuine quantum features of nano-mechanical motion is a key goal for both fundamental and applied quantum science. To this end, a promising approach is the stabilization of nonclassical features in the presence of dissipation, by means of the tunable coupling with a photonic environment. Here we present a scheme that combines dissipative squeezing with a mechanical nonlinearity to stabilize arbitrary approximations of (displaced) mechanical Fock state of any number. We consider an optomechanical system driven by three control lasers—at the cavity resonance and at the two mechanical sidebands—that couple the amplitude of the cavity field to the resonator’s position and position squared. When the amplitude of the resonant drive is tuned to some specific values, the mechanical steady state is found in a (displaced) superposition of a finite number of Fock states, which for large enough squeezing achieves near-unit fidelity with a (displaced) Fock state of any desired number.
1. Introduction
The motional state of atomic or mechanical degrees of freedom can be manipulated via the interaction with the electromagnetic field confined in a cavity. Such a possibility is best illustrated by cavity cooling, which has been successfully applied to single atoms [1], ions [2], and micro- and nano-mechanical resonators [3,4,5]. Recent breakthroughs in the dissipative preparation of mechanical squeezed states [6,7,8,9], where a cavity-assisted scheme is designed to cool the target system directly into a squeezed state of motion, can be thought of as a powerful development of this paradigm [10,11,12,13,14]. However, for many applications, ranging from fundamental tests of quantum mechanics to quantum information precessing, the stabilization of highly pure states with non-Gaussian features is needed instead. In cavity optomechanics, the quadratic optomechanical coupling has been exploited for the dissipative preparation of Schrödinger cat states [15,16], but the existence of multiple steady states requires the unpractical initialization of the system in a state of definite parity. Recently we have shown that a tunable optomechanical coupling which has both a linear and quadratic component enables the stabilization of pure non-Gaussian states without requiring any initialization [17,18]. For specific values of the amplitude of the laser drives new families of nonclassical states can be stabilized, which correspond to (squeezed and displaced) superpositions of a finite number of Fock states. Here we focus on a specific instance, namely on one such (displaced) finite superposition that approximates—in principle with arbitrary fidelity—any number state in the harmonic ladder (modulo a displacement).
2. Results
We consider an optomechanical system where the frequency of a cavity mode parametrically couples to the displacement and squared displacement of a mechanical resonator. The Hamiltonian is given by (we set throughout)
where () is the annihilation operator of the cavity (mechanical) mode of frequency () and , respectively quantifies the linear and quadratic single-photon coupling. Such linear-and-quadratic coupling can be realized in membrane-in-the-middle setups [19,20,21], cold atoms [22], microdisk resonators [23] and photonic crystal cavities [24,25]. The cavity has a decay rate and is driven with three tones
applied on the cavity resonance (), and on the lower and upper mechanical sideband . After standard linearization (we dub the fluctuation operator of the cavity field), moving into a frame rotating with the free cavity and mechanical Hamiltonian, and focusing on the good cavity limit () we get
where we set , , and are the steady values of the cavity amplitude at each frequency component; we will assume these couplings to be real and positive without loss of generality. After a transient time the cavity field is found in the vacuum while the mechanical resonator in a pure state that satisfies the condition
Note that when the nonlinear term in absent, namely , we recover dissipative squeezing with a squeezing degree [11].
In order to characterize the steady state , let us first assume that the amplitudes at the two mechanical sidebands are equal, i.e., . In this case it is enough to notice that for the following values of the resonant coupling
the condition expressed in Equation (4) becomes
where is the displacement operator and a non-negative integer (to stress this dependence we set from now on). This is in turn equivalent to
and proves that the steady state is indeed a displaced Fock state. In particular, by tuning the amplitude of the resonant drive in Equation (5) any state in the Fock state ladder can be stabilized.
The class of steady states obtained in Equation (7) turns out to be unstable [18]. However, it can be seen as the limit of the more general case with
which is guaranteed to be stable as long as . In order to find the new steady state, we can project Equation (4) onto the position eigenstate and obtain a differential equation for the associated wave function . The solution of such equation reads
where we set . Note that the integer order of the Hermite polynomial is determined by the resonant coupling in Equation (8). By completing the square in the exponent we get
where . Note that for we correctly recover the wave function of a displaced quantum harmonic oscillator. We now exploit the following property of the Hermite polynomials, which leads us to
with . From the last line we can finally read the explicit expression of the state
where the normalization factor is given by . The steady state is now given by the action of a n-dependent displacement on a superposition of a finite number () of elements. It is easily checked that in the limit the superposition collapses to the single element of Equation (7). On the other hand, for any non-zero value of the squeezing parameter the state displays negativity in the Wigner distribution and the larger the amount squeezing the closer the resemblance with a Fock state. This feature is clear from Figure 1, where we show the Wigner distribution for a given n () and different values of the squeezing parameter . We clearly see that the distribution, which for lower values of is skewed toward one side, progressively straightens to approach that of a Fock state. We can thus think of as a state that approximates any given displace Fock state, to an extent that improves with the amount of squeezing available. Mechanical dissipation—not considered here—sets a limit on the precision of such approximation. Yet, one can show that it is still possible to approximate with near-unit fidelity any Fock state [18].
Coming back to Equation (4), we notice that is the state uniquely annihilated by the nonlinear operator
where is a Bogoliubov mode and . The nonlinear contribution added to the Bogoliubov transformation makes the nature of non bosonic.
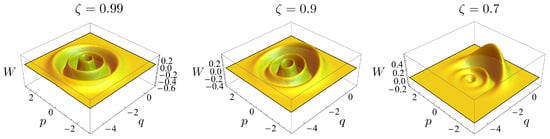
Figure 1.
Wigner function of the state for different values (left), (centre), (right).
3. Discussion
We presented an exactly solvable model to augment dissipative squeezing by means of a quadratic nonlinearity. The model can be implemented in optomechanical cavity and the states stabilized by our protocol approximate displaced multi-phonon Fock state of any desired number.
Acknowledgments
M.B. is supported by the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 732894 (FET Proactive HOT). O. H. acknowledges support from the SFI-DfE Investigator programme (grant 15/IA/2864), the EU Horizon2020 Collaborative Project TEQ (grant agreement No. 766900) and from the EPSRC project EP/P00282X/1.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsor had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Maunz, P.; Puppe, T.; Schuster, I.; Syassen, N.; Pinkse, P.W.H.; Rempe, G. Cavity cooling of a single atom. Nature (Lond.) 2004, 428, 50–52. [Google Scholar] [CrossRef] [PubMed]
- Leibrandt, D.R.; Labaziewicz, J.; Vuletić, V.; Chuang, I.L. Cavity Sideband Cooling of a Single Trapped Ion. Phys. Rev. Lett. 2009, 103, 103001. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.; Alegre, T.P.M.; Safavi-Naeini, A.H.; Hill, J.T.; Krause, A.; Gröblacher, S.; Aspelmeyer, M.; Painter, O. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 2011, 478, 89–92. [Google Scholar] [CrossRef] [PubMed]
- Teufel, J.D.; Donner, T.; Li, D.; Harlow, J.W.; Allman, M.S.; Cicak, K.; Sirois, A.J.; Whittaker, J.D.; Lehnert, K.W.; Simmonds, R.W. Sideband cooling of micromechanical motion to the quantum ground state. Nature 2011, 475, 359–363. [Google Scholar] [CrossRef]
- Verhagen, E.; Delèglise, S.; Weis, S.; Schliesser, A.; Kippenberg, T.J. Quantum-coherent coupling of a mechanical oscillator to an optical cavity mode. Nature 2012, 482, 63–67. [Google Scholar] [CrossRef]
- Wollman, E.E.; Lei, C.U.; Weinstein, A.J.; Suh, J.; Kronwald, A.; Marquardt, F.; Clerk, A.A.; Schwab, K.C. Quantum squeezing of motion in a mechanical resonator. Science 2015, 349, 952–955. [Google Scholar] [CrossRef]
- Pirkkalainen, J.-M.; Damskägg, E.; Brandt, M.; Massel, F.; Sillanpää, M.A. Squeezing of quantum noise of motion in a micromechanical resonator. Phys. Rev. Lett. 2015, 115, 243601. [Google Scholar] [CrossRef]
- Lecocq, F.; Clark, J.B.; Simmonds, R.W.; Aumentado, J.; Teufel, J.D. Quantum nondemolition measurement of a nonclassical state of a massive object. Phys. Rev. X 2015, 5, 041037. [Google Scholar] [CrossRef]
- Kienzler, D.; Lo, H.-Y.; Keitch, B.; de Clercq, L.; Leupold, F.; Lindenfelser, F.; Marinelli, M.; Negnevitsky, V.; Home, J.P. Quantum harmonic oscillator state synthesis by reservoir engineering. Science 2015, 347, 6217. [Google Scholar] [CrossRef]
- Poyatos, J.F.; Cirac, J.I.; Zoller, P. Quantum reservoir engineering with laser cooled trapped ions. Phys. Rev. Lett. 1996, 77, 4728. [Google Scholar] [CrossRef]
- Kronwald, A.; Marquardt, F.; Clerk, A.A. Arbitrarily large steady-state bosonic squeezing via dissipation. Phys. Rev. A 2013, 88, 063833. [Google Scholar] [CrossRef]
- Wang, Y.-D.; Clerk, A.A. Reservoir-engineered entanglement in optomechanical systems. Phys. Rev. Lett. 2013, 110, 253601. [Google Scholar] [CrossRef] [PubMed]
- Woolley, M.J.; Clerk, A.A. Two-mode squeezed states in cavity optomechanics via engineering of a single reservoir. Phys. Rev. A 2014, 89, 063805. [Google Scholar] [CrossRef]
- Li, J.; Haghighi, I.M.; Malossi, N.; Zippilli, S.; Vitali, D. Generation and detection of large and robust entanglement between two different mechanical resonators in cavity optomechanics. New J. Phys. 2015, 17, 103037. [Google Scholar] [CrossRef]
- Tan, H.; Bariani, F.; Li, G.; Meystre, P. Generation of macroscopic quantum superpositions of optomechanical oscillators by dissipation. Phys. Rev. A 2013, 88, 023827. [Google Scholar] [CrossRef]
- Asjad, M.; Vitali, D. Reservoir engineering of a mechanical resonator: Generating a macroscopic superposition state and monitoring its decoherence. J. Phys. B 2014, 47, 045502. [Google Scholar] [CrossRef]
- Brunelli, M.; Houhou, O.; Moore, D.W.; Nunnenkamp, A.; Paternostro, M.; Ferraro, A. Unconditional preparation of nonclassical states via linear-and-quadratic optomechanics. Phys. Rev. A 2018, 98, 063801. [Google Scholar] [CrossRef]
- Brunelli, M.; Houhou, O. Linear and quadratic reservoir engineering of non-Gaussian states. Phys. Rev. A 2019, 100, 013831. [Google Scholar] [CrossRef]
- Thompson, J.D.; Zwickl, B.M.; Jayich, A.M.; Marquardt, F.; Girvin, S.M.; Harris, J.G.E. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature 2008, 452, 72. [Google Scholar] [CrossRef]
- Sankey, J.C.; Yang, C.; Zwickl, B.M.; Jayich, A.M.; Harris, J.G.E. Strong and tunable nonlinear optomechanical coupling in a low-loss system. Nat. Phys. 2010, 6, 707–712. [Google Scholar] [CrossRef]
- Purdy, T.P.; Brooks, D.W.C.; Botter, T.; Brahms, N.; Ma, Z.-Y.; Stamper-Kurn, D.M. Tunable cavity optomechanics with ultracold atoms. Phys. Rev. Lett. 2010, 105, 133602. [Google Scholar] [CrossRef] [PubMed]
- Karuza, M.; Galassi, M.; Biancofiore, C.; Molinelli, C.; Natali, R.; Tombesi, P.; di Giuseppe, G.; Vitali, D. Tunable linear and quadratic optomechanical coupling for a tilted membrane within an optical cavity: Theory and experiment. J. Opt. 2012, 15, 025704. [Google Scholar] [CrossRef]
- Doolin, C.; Hauer, B.D.; Kim, P.H.; MacDonald, A.J.R.; Ramp, H.; Davis, J.P. Nonlinear optomechanics in the stationary regime. Phys. Rev A 2014, 89, 053838. [Google Scholar] [CrossRef]
- Paraïso, T.K.; Kalaee, M.; Zang, L.; Pfeifer, H.; Marquardt, F.; Painter, O. Position-squared coupling in a tunable photonic crystal optomechanical cavity. Phys. Rev. X 2015, 5, 041024. [Google Scholar] [CrossRef]
- Kalaee, M.; Paraïso, T.K.; Pfeifer, H.; Painter, O. Design of a quasi-2D photonic crystal optomechanical cavity with tunable, large x2-coupling. Opt. Express 2016, 24, 21308. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).