2. The Model and Its Entanglement Properties
We study an isolated system , with and , where are qubits, i.e., quantum systems whose Hilbert spaces are two-dimensional, while are such that dim, with integer numbers much larger than unity. Overall it is dim, dim, and dim. In what follows the qubits will be described by the Pauli operators such that , with , and . As for A and B, they will be represented in terms of spin operators such that , with , and . The total system is assumed isolated, and hence in a pure state at all time. The device is prepared in a state featuring some internal entanglement, meaning that and are entangled. On the other hand, we take and independent from each other, and separately coupled with D, i.e., with and , via an interaction upon which we do not make assumptions.
In this setting, the state
at whatever time after the interaction starts can be written as
where
,
and
are orthonormal bases for the Hilbert spaces of
D,
A, and
B, respectively. The complex coefficients
and
satisfy
, due to the normalization of
. The form (
1) ensures that the state of
M is separable [
1], meaning that there is no entanglement between
and
. For the sake of a lighter notation and without loss of generality, we set
.
Aim of the following analysis is to understand how the internal entanglement depends on the spin-values
S, particularly when the condition of large-
S is enforced on both
A and
B. To this respect, we remind that a spin-
S system exhibits a classical-like behaviour when
[
2], which implies the vanishing of any sort of quantum correlations, including entanglement, with other systems; we hence expect
M to disentangle from
D when
S increases. In order to check whether this process can effectively protect the internal entanglement we proceed as follows.
We first conjecture that the coefficients entering the state (
1) have the following form in the large-
S limit
where
and
are decreasing functions of
S,
, such that
while
is the normalization factor that goes to 1 in the large-
S limit. Moreover, in order to make our analytical results more readable, we restrict ourselves to the case when the qubit pair is confined to the two-dimensional Hilbert subspace generated by two of the four states
, namely
and
(we choose the indexes 3 and 4 to avoid confusion with the qubit labels, 1 and 2).
We can now determine the explicit expression for the concurrence
relative to the state
, which is a proper measure [
3] of the internal entanglement, i.e., the one between
and
. Notice that the concurrence can be here used to study the internal entanglement because
D is made of a qubit-pair, i.e., the only system for which the concurrence relative to a mixed state is defined.
Referring to the state (
1), using the form (
2) with
only, and understanding the
S dependence, we finally find
Another useful entanglement measure that we take into consideration is the one-tangle
, which quantifies the entanglement between a qubit and whatever else determines its state
, according to
[
4]. In our setting, we use it to evaluate how much entanglement one of the two qubits of
D shares with the system made of
M and the other qubit. Its explicit form reads
where the last equation follows from the symmetry of the setting w.r.t. to the swap
. It is important to notice that while the concurrence
quantifies just the useful internal entanglement that allows the device
D to function efficiently, the one tangle
incorporates some useless external entanglement, and comparing the twos can help quantifying the detrimental effect of
M upon the qubit-pair entanglement, as further commented upon in the concluding section.
In order to evaluate
and
from Equations (
4) and (
5) one has to choose the coefficients
, and
. In order to keep our analysis as general as possible, for each value of
S, we have repeated the calculation of both quantities for 200 times, each time using a different set of coefficients,
randomly generated according to
and
,
,
. The average of the 200 values thus obtained for
, and
, is then taken as the, respective, proposed result. In fact, reminding the
S-dependence that we have understood in the above coefficients, we have further enforced the condition (
3) by taking
, with
, and the same for
. As for
and
we have put them both equal to
.
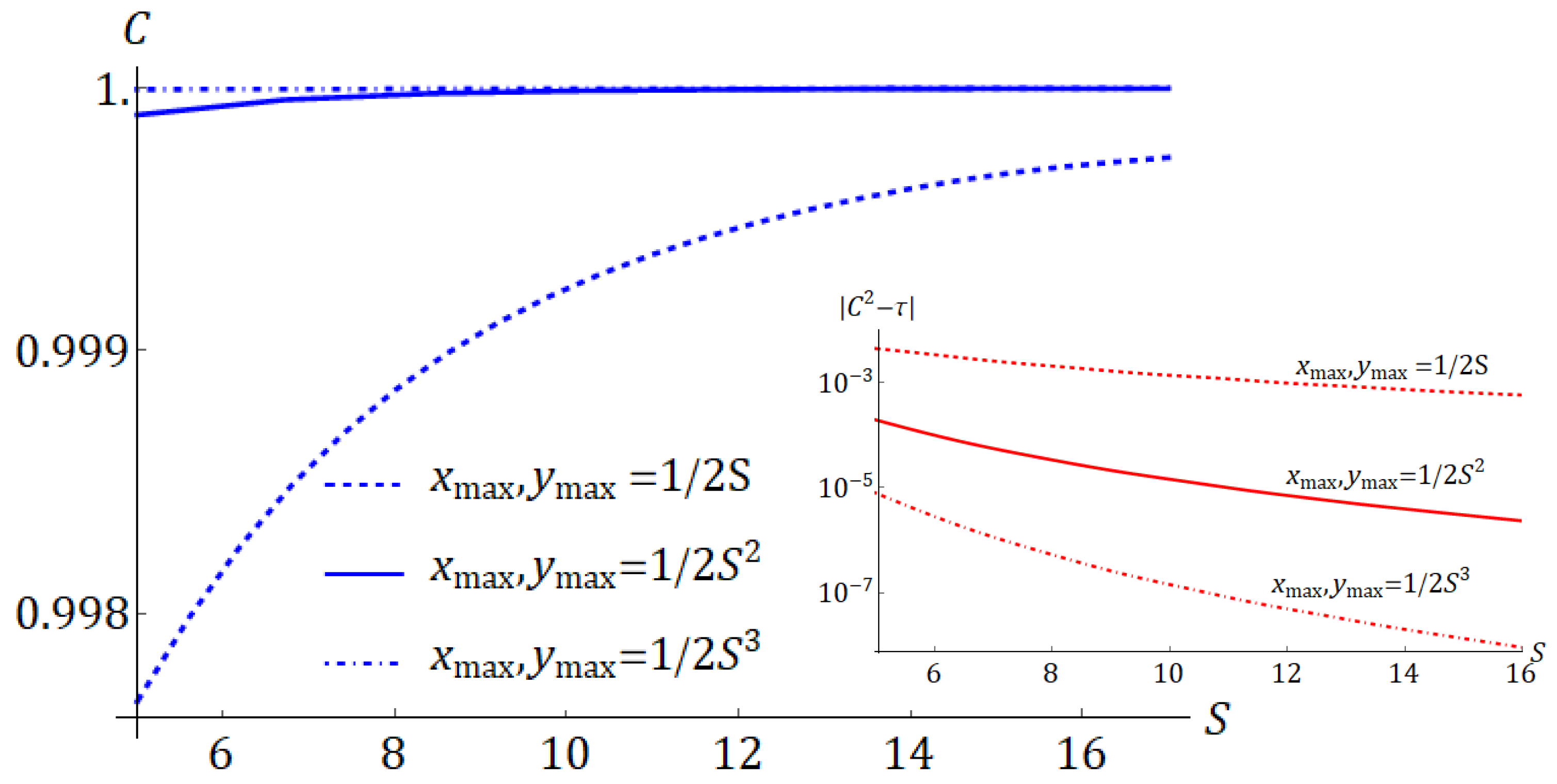
In
Figure 1 we show
as a function of
S, and
. We see that, even in the worse case,
, the internal entanglement increases with
S. In order to check whether a larger internal entanglement can be actually due to a reduction of the external one, in the inset of
Figure 1 we show the difference
, that provides an estimate of the internal-entanglement squandering due to the onset of quantum correlations between
D and
M. It is clearly seen, both for
and 2, that a large value of
S prevents the above onset, resulting in an effective protection of internal entanglement.
3. Discussion
In the above section we have introduced the idea that taking a large value of
S might help protecting the internal entanglement, as it induces a classical-like behaviour for
M, and hence a net reduction of its quantum correlations with
D. However, this argument only works if one assumes that some constraint upon the entanglement between, say,
, and other quantum systems holds. In fact, one such constraint exists and usually goes under the name of “monogamy of entanglement”, analytically expressed by inequalities taking different forms depending on the specific case considered. In the case of
N qubits in a pure state, it is expressed by
where
is the one-tangle between
and the other
qubits. Although the above expression does not fit our situation, as we are not dealing with
N qubit, we can use it as follows (we still take
for the sake of simplicity).
In order for the physical objects that model
M to be described as spin-
S systems they must be made of a set of qubits
, with
and
, coupled amongst themselves in a way such that the total spin of the set keeps the constant value
S. In our setting, this translates Equation (
6) into
Although we cannot limit the sums entering the above equation by using Equation (
6) again, as this exclusively hold for qubits in a pure state while
is in a mixed one, yet we can understand that one possibility for Equation (
7) to stay meaningful as
, i.e.,
, is that both sums it contains do vanish. In fact, this can be analytically demonstrated by enforcing the condition (
3) into Equations (
4) and (
5) via neglecting all powers of order 2 and higher in the coefficients
and
. This leads to
which implies that
is entangled almost exclusively with
if
as
M becomes macroscopic, consistently with the idea that large-
S systems do not share quantum correlations [
5].
This work confirms that a good strategy for protecting the internal entanglement of a quantum device D is that of making its control/reading apparatus M to feature a semi-classical behaviour, by this meaning that it still admits a quantum-mechanical description, so as to keep talking with the device, but with genuinely quantum properties, such as entanglement, already on the verge of depletion. In fact, in order to test this strategy, we are specifically considering the case when M is a many-body spin-system dynamically driven near a quantum critical point, where the mechanism of domain-formation might indeed induce a semi-classical behaviour as described above. Related work is in progress.