Thermodynamics and Fluctuations-Correlations of Conserved Charges in a Hadron Resonance Gas Model with Attractive and Repulsive Interaction within S-Matrix Formalism ^†

Abstract

We have extended the hadron resonance gas (HRG) model by including the effect of both attractive and repulsive interaction in the scattering matrix (S-matrix) formalism. The attractive part of the interaction is calculated using K-matrix formalism while the repulsive part is included by fitting to experimental phase shifts. We have calculated various thermodynamics quantities like pressure, energy density, entropy density etc. A good agreement between our calculations and the hadronic phase of the lattice QCD (LQCD) simulations is observed. We have also calculated fluctuations and correlations for various conserved charges like baryon, strangeness and electric charge. In the present model, ${\chi }_B^2$, ${\chi }_{BS}^{11}$ and $C_{BS}$ agree well with the LQCD data.

1. Introduction

The primary goals of experiments with heavy-ion beams at ultrarelativistic energies is to study the possible formation of a new form of matter known as the quark-gluon plasma (QGP) and the possible occurrence of a phase transition between the QGP and hadronic phases. An approach to study the properties of hadronic phase formed by hadronization of the QGP is through a statistical thermal model of a gas of hadrons called the hadron resonance gas (HRG) model [1,2]. The ideal HRG model assumes that the thermal system consists of point like non interacting hadrons and resonances. There are several approaches to include interaction in the HRG model. For example, in the excluded volume HRG (EVHRG) model, van der Waals (VDW) type repulsive interaction is introduced by considering the geometrical sizes of the hadrons [3]. Both attractive and repulsive van der Waals interactions have also been introduced in the VDWHRG model [4]. However, these models introduces more parameters to include interactions. In this present work we have included interaction using the S-matrix approach without introducing any additional parameters.

2. Formalism

The most natural way to incorporate interaction among a gas of hadrons is to use relativistic virial expansion introduced in Ref. [5]. In this approach, the total pressure of the system is the sum of non-interacting (ideal) and interacting parts, i.e,

$$P=P_{\mathrm{id}}+P_{\mathrm{int}}.$$

(1)

We consider baryon and meson octets as the stable hadrons. Non interacting stable hadrons contribute to the ideal part of the pressure whereas two body elastic scattering between any two stable hadrons gives the interacting part of the pressure. The non-interacting part of the pressure in a grand canonical ensemble can be written as

$$\begin{array}{c}\hfill P_{\mathrm{id}}=\sum _h\frac{g_h}{2{\pi }^2}{m}_h^2{T}^2\sum _{j=1}^{\infty }{(\pm 1)}^{j-1}(z^j/j^2)K_2\left(j\beta m_h\right),\end{array}$$

(2)

where sum is over all the stable hadrons considered in this work, $m_h,g_h$ are the mass and degeneracy of the hadron, T is the temperature of the system, $K_2$ is the modified Bessel function of second kind, $\beta$ is the inverse of T. In the last expression $z=e^{\beta {\mu }_h}$ is the fugacity where ${\mu }_h$ is the chemical potential of hth hadron and is defined as ${\mu }_h=B_h{\mu }_B+S_h{\mu }_S+Q_h{\mu }_Q$ where $B_h$, $S_h$, $Q_h$ are baryon number, strangeness and electric charge and $\mu$’s are the respective chemical potentials. The interacting part of the pressure can be written as [6]

$$\begin{array}{c}\hfill \begin{array}{c}\hfill P_{\mathrm{int}}=\frac{z_1{z}_2}{2{\pi }^3{\beta }^2}{\int }_M^{\infty }d\epsilon {\epsilon }^2{K}_2\left(\beta \epsilon \right)\sum _{I,L}{}^{{}^{\prime }}{g}_{I,L}\frac{\partial {\delta }^{I,L}\left(\epsilon \right)}{\partial \epsilon },\end{array}\end{array}$$

(3)

where $z_1$ and $z_2$ are fugacities of two species, ${\delta }^{I,L}$ is the phase shift, I and L denote isospin and angular momentum respectively, $\epsilon$ is the center of mass energy. The factor $g_{I,L}=(2I+1)(2L+1)$ is the degeneracy factor, M is the invariant mass of the interacting pair at threshold. The prime over the summation sign denotes that for given L the sum over I is restricted to values consistent with statistics. For the attractive (repulsive) interactions derivative of phase shifts are positive (negative).

Once we know the pressure, we can calculate different thermodynamic quantities. The susceptibilities of conserved charges can be calculated as

$${\chi }_{BSQ}^{xyz}=\frac{{\partial }^{x+y+z}(P/T^4)}{\partial {({\mu }_B/T)}^x\partial {({\mu }_S/T)}^y\partial {({\mu }_Q/T)}^z},$$

(4)

where x, y and z are the order of derivatives of the quantities B, S and Q.

2.1. Attractive Interaction Using K-Matrix Formalism

A theoretical way of calculating the attractive phase shifts is to use the K-matrix formalism. The inverse of K-matrix is defined as ${\mathbb{K}}^{-1}={\mathbb{T}}^{-1}+i\mathbb{I}$ where $\mathbb{I}$ is the unit matrix. The transfer matrix $\mathbb{T}$ is related to the S-matrix by the relation $\mathbb{S}=\mathbb{I}+2i\mathbb{T}$. The K-matrix formalism preserves the unitarity of S-matrix and neatly handles multiple resonances [7]. In addition to that, widths of the resonances are handled naturally in the above formalism. For overlapping resonances the K-matrix gives a more accurate description of the phase shifts than the Breit-Wigner parametrization. In Ref. [8] the K-matrix formalism was used to study an interacting gas of hadrons and it was extended further in Ref. [9].

The resonances, contributing to the process $ab\to R\to ab$, appear as a sum of poles in the K-matrix,

$$K_{R\to ab}^{I,L}=\sum _{R(I,L)}\frac{m_R{\Gamma }_{R\to ab}\left(\epsilon \right)}{m_R^2-{\epsilon }^2},$$

(5)

where a, b are hadrons, $m_R$, ${\Gamma }_{R\to ab}$ are the mass and partial width of the resonance. We have considered energy dependent partial widths ${\Gamma }_{R\to ab}\left(\epsilon \right)$ [7], i.e., the total width times the branching ratio for the channel $R\to ab$. The sum in the last expression is restricted to the addition of resonances for a given angular momentum L and isospin I. We have considered resonances which decay into two stable hadrons [10]. Once one computes the K-matrix by providing the relevant masses and widths of resonances, the phase shift can obtained using the relation ${\delta }^{I,L}={tan}^{-1}{K}^{I,L}.$ Then using Equation (3) one can calculate $P_{int}$.

2.2. Interaction Using Experimental Phase Shift

For repulsive interactions and for interactions where the information about $m_R$ and ${\Gamma }_R$ are not available the K-matrix formalism is not applicable. For those cases we taken the phase shifts information from experimental data and used them directly in Equation (3) to calculate thermodynamical quantities. For repulsive ($\pi N$, $KN$) and nucleon-nucleon ($NN$) interaction phase shifts we use the data from the SM16 partial wave analysis [11]. For the repulsive isotensor channel ${\delta }_0^2$ in the $\pi \pi$ scattering we use the data from Ref. [12].

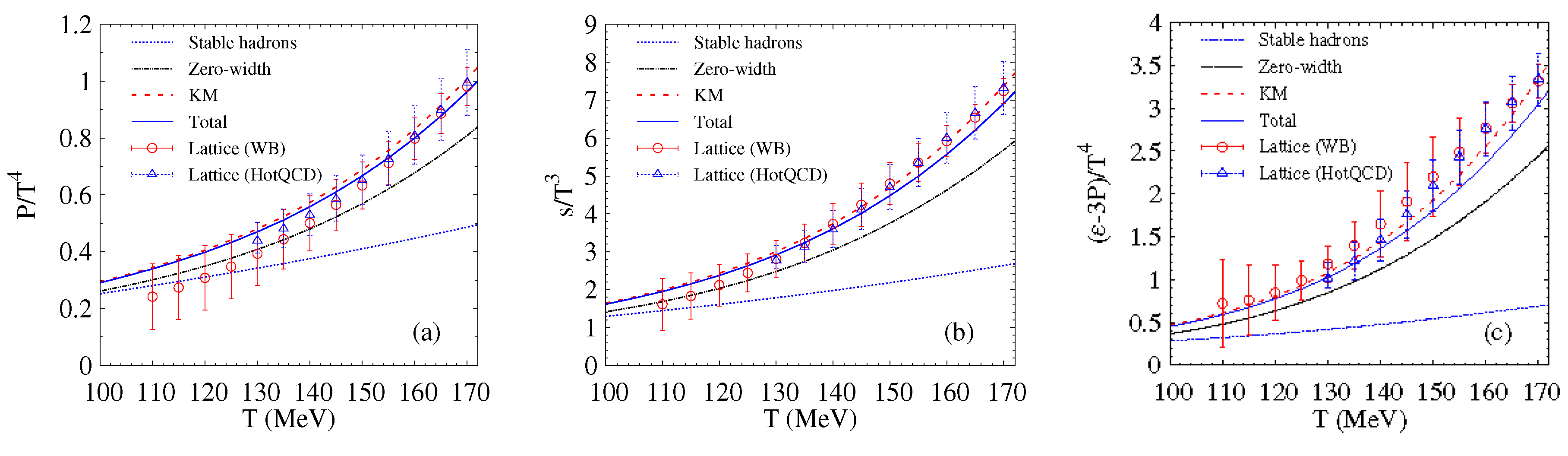
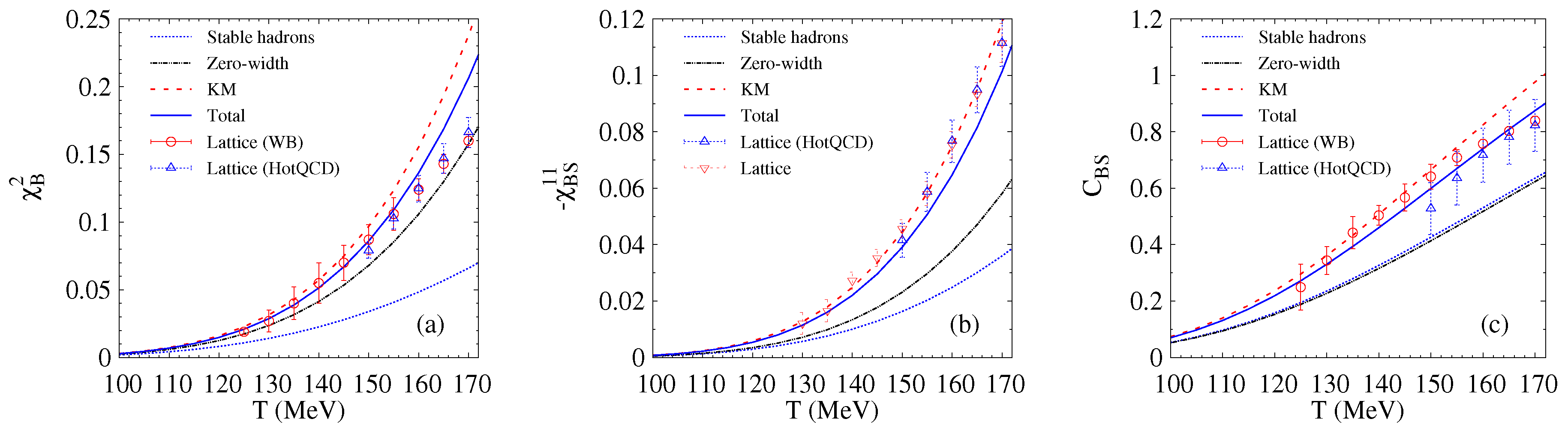
3. Results and Discussion

Figure 1 shows the temperature dependence of normalized pressure ($P/T^4$), entropy density ($s/T^3$) and the interacting measure ($(\epsilon -3P)/T^4$) at zero chemical potential [13]. Both ‘Stable hadrons’ and ‘Zero-width’ correspond to the results of non interacting HRG model. For ‘Stable hadrons’ we consider only the stable baryon and meson octets whereas for ‘Zero-width’ we consider stable hadrons and resonances as used in K-matrix formalism. So differences between these two results are due to the resonances present in the model. ‘Total’ contains both the attractive and repulsive interaction whereas ‘KM’ contains only the attractive part. Both ’KM’ and ’Total’ contain non interacting part (stable hadrons) as well. All the thermodynamic quantities shown in this figure increase as we include the attractive interaction (see the differences between ‘Zero-width’ and ‘KM’). Further, these quantities decrease slightly (‘Total’) when we include repulsive interaction. The effect of attractive interaction is larger compared to the repulsive interaction and hence the thermodynamic quantities in presence of both attractive and repulsive interaction (‘Total’) are larger compared to the results of ’Zero-width’. We compare our results with LQCD data of Refs. [14,15]. We observe that the interacting model (‘Total’) provides a satisfactory description in the hadronic phase of LQCD data.

The effect of interactions are most prominent when we calculate second order susceptibilities. Figure 2 shows the variation of ${\chi }_B^2$, ${\chi }_{BS}^{11}$ and $C_{BS}$ with temperature at zero chemical potential. Effect of both attractive and repulsive interactions are strong in these quantities. From our present analysis we observe that the strength of the repulsive interaction has the following order $\pi N>KN>NN$. Results are compared with LQCD data of Refs. [2,16,17]. Results for ${\chi }_B^2$, ${\chi }_{BS}^{11}$ and $C_{BS}$ (−3 ${\chi }_{BS}^{11}$/${\chi }_S^2$) agree well with the LQCD data, in the case when both attractions and repulsions are taken into account.