Fluctuations and Azimuthally Dependent Two-Particle Distributions ^†

Abstract

The azimuthal dependence of the two-particle distribution, which reflects both the anisotropic flow of each particle and azimuthally sensitive correlations between the two particles, can be characterized with Fourier coefficients. We illustrate on a few idealized examples how the corresponding ”pair-flow coefficients” are affected by fluctuations of the single-particle anisotropic flow, even if genuine correlations are absent.

1. Introduction

Information on the physics at play in the expanding fireball created in ultrarelativistic collisions of heavy nuclei can only be accessed by investigating the distributions of outgoing particles in the final state. In an event, the single-particle azimuthal probability distribution $p_1\left(\phi \right|\left\{{\psi }_n\right\})$ of emitted particles is conveniently expressed in terms of the well-known Fourier expansion

$$p_1\left(\phi \right|\left\{{\Psi }_n\right\})=\frac{1}{2\pi }\left[1+\sum _{n=1}^{\infty }2v_{n}cos\left[n(\phi -{\Psi }_n)\right]\right],$$

(1)

Here and in the following, we drop the dependence of probability distributions or the associated Fourier coefficients on the transverse momentum of the outgoing particles.

One can also consider the two-particle probability distribution $p_2({\phi }_a,{\phi }_b|\left\{{\Psi }_n\right\})$ that a first particle a be measured with azimuth ${\phi }_a$ and a second one (b) with azimuth ${\phi }_b$. Generically, the two-particle distribution can be decomposed as the sum of a “trivial” factorized component $p_1\left({\phi }_a\right|\left\{{\Psi }_n\right\})p_1\left({\phi }_b\right|\left\{{\Psi }_n\right\})$, which represents the independent emission of particles governed by Equation (1), and a “connected part” $p_{2,\mathrm{c}}({\phi }_a,{\phi }_b|\left\{{\Psi }_n\right\})$ that stems from genuine two-body correlations between the two particles. Naively, the latter signal can be isolated by subtracting the background factorized term from the two-particle distribution. However, in a realistic sample of events the single-particle flow coefficients $v_n$ and the orientations $\left\{{\Psi }_n\right\}$ of the symmetry planes vary event by event, which significantly complicates the issue.

In these proceedings, we recall how the two-particle probability distribution, and in particular its azimuthal dependence, can be characterized by a set of Fourier coefficients [1]. For uncorrelated particles, these “pair flow” coefficients are entirely determined by the single-particle flow harmonics $v_n$, and we illustrate on a simple example how event-by-event fluctuations of the latter will affect the former.

2. Pair Flow Coefficients

2.1. Definition

In practical studies, one is not so much interested in the dependence of the pair distribution $p_2$ on the particle azimuths ${\phi }_a$, ${\phi }_b$. Instead, the pair is characterized by a relative angle $\Delta \phi$ and a characteristic pair angle ${\phi }^{\mathrm{pair}}$, which can be for instance the azimuth of the leading particle with highest transverse momentum (in jet-like correlation studies) or that of the total momentum of the pair (in femtoscopy studies). The two-particle distribution is then studied as a function of $\Delta \phi$ and—if one is interested in azimuthally sensitive correlations—${\phi }^{\mathrm{pair}}$, resulting in a probability density $p_2({\phi }^{\mathrm{pair}},\Delta \phi |\left\{{\Psi }_n\right\})$.

As was argued in Ref. [1], a set of robust observables to characterize the dependence on the azimuthal angle ${\phi }^{\mathrm{pair}}$ consists of Fourier “pair flow” coefficients, similar to those used in Equation (1), namely such that

$$p_2({\phi }^{\mathrm{pair}},\Delta \phi |\left\{{\Psi }_n\right\})\propto 1+\sum _{n=1}^{\infty }2\left(v_{n,c}^{\mathrm{pair}}(\Delta \phi )cos\left[n({\phi }^{\mathrm{pair}}-{\Psi }_n)\right]+v_{n,s}^{\mathrm{pair}}(\Delta \phi )sin\left[n({\phi }^{\mathrm{pair}}-{\Psi }_n)\right]\right)$$

(2)

with coefficients

$$\begin{array}{cc}\hfill v_{n,c}^{\mathrm{pair}}(\Delta \phi )& =\int p_2({\phi }^{\mathrm{pair}},\Delta \phi |\left\{{\Psi }_n\right\})cos\left[n({\phi }^{\mathrm{pair}}-{\Psi }_n)\right]\frac{d{\phi }^{\mathrm{pair}}}{2\pi },\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill v_{n,s}^{\mathrm{pair}}(\Delta \phi )& =\int p_2({\phi }^{\mathrm{pair}},\Delta \phi |\left\{{\Psi }_n\right\})sin\left[n({\phi }^{\mathrm{pair}}-{\Psi }_n)\right]\frac{d{\phi }^{\mathrm{pair}}}{2\pi }\hfill \end{array}$$

(4)

which depend on the relative angle $\Delta \phi$. As discussed in Ref. [1], even for a non-fluctuating geometry of the initial state there is no ${\phi }^{\mathrm{pair}}-{\Psi }_n\leftrightarrow -({\phi }^{\mathrm{pair}}-{\Psi }_n)$ symmetry in the system, so that the sine coefficients $v_{n,s}^{\mathrm{pair}}$ are in general different from zero. In addition, every method used to measure the single-particle flow harmonics $v_n$ is automatically applicable to the pair flow coefficients $v_{n,c}^{\mathrm{pair}}$, $v_{n,s}^{\mathrm{pair}}$.

To fix ideas, we consider in the following ${\phi }^{\mathrm{pair}}=({\phi }_a+{\phi }_b)/2$ and $\Delta \phi \equiv {\phi }_a-{\phi }_b$, such that ${\phi }_a={\phi }^{\mathrm{pair}}+\Delta \phi /2$ and ${\phi }_b={\phi }^{\mathrm{pair}}-\Delta \phi /2$.

2.2. Pair Flow Coefficients for Uncorrelated Particles

When particles a and b are uncorrelated, so that $p_2({\phi }_a,{\phi }_b|\left\{{\Psi }_n\right\})=p_1\left({\phi }_a\right|\left\{{\Psi }_n\right\})p_1\left({\phi }_b\right|\left\{{\Psi }_n\right\})$, one can readily compute the resulting pair flow coefficients and express them in terms of the single-particle harmonics $\left\{v_n\left(a\right)\right\}$, $\left\{v_{n^{\prime }}\left(b\right)\right\}$, where for the sake of generality we allow different coefficients for the two particles (The symmetry planes associated with the two particles are still supposed to coincide, ${\Psi }_n\left(a\right)={\Psi }_n\left(b\right)$). After some straightforward but lengthy algebra, one finds for instance

$$\begin{array}{c}{v}_{n,c}^{\mathrm{pair}}(\Delta \phi )=\frac{\left[v_n\left(a\right)+v_n\left(b\right)\right]}{2}cos\frac{n\Delta \phi }{2}+\sum _{\underset{p\ne 0,n}{p=-\infty }}^{\infty }{v}_p\left(a\right)v_{n-p}\left(b\right)cos\left[p{\Psi }_p+(n-p){\Psi }_{n-p}-n{\Psi }_n+\frac{n-2p}{2}\Delta \phi \right]\end{array}$$

(5)

where we use the convention $v_q\equiv v_{-q}$ for negative values of q. This result illustrates explicitly that the pair flow coefficients still depend on the relative angle $\Delta \phi$. An additional dependence on $\Delta \phi$ is contained in the global denominator entering the calculation of $v_{n,c}^{\mathrm{pair}}$, which was omitted from Equation (5).

Considering an idealized simple example for which only $v_2$ is non-zero at the single-particle level, Equation (5) shows that this gives rise to both a second harmonic $v_{2,c}^{\mathrm{pair}}$ and a fourth harmonic $v_{4,c}^{\mathrm{pair}}$ modulation of the two-particle distribution, with $v_{4,c}^{\mathrm{pair}}\propto v_2\left(a\right)v_2\left(b\right)cos\left[4({\Psi }_2-{\Psi }_4)\right]$ (This term should not be confused with the similar-looking term $2v_2\left(a\right)v_2\left(b\right)cos(2\Delta \phi )$ which is the second harmonic of the dependence on $\Delta \phi$ of the ${\phi }^{\mathrm{pair}}$-averaged two-particle distribution).

2.3. Fluctuations of Single-Particle and Pair Flow

In Section 2.2 we assumed fixed values of the single-flow coefficients $v_n$ and of the orientations $\left\{{\Psi }_n\right\}$ of the symmetry planes, which is not what one finds in a typical set of experimental events. The remainder of these proceedings is devoted to a preliminary investigation of the effect of event-by-event fluctuations.

Let us first discuss fluctuations of the symmetry plane angles. Obviously, they can only affect the terms of the sum on the right hand side of Equation (5). For unpolarized colliding nuclei, each ${\Psi }_n$ should be arbitrarily, equally distributed, yet there can still be correlations between the orientations of different symmetry planes in a given event—in particular between ${\Psi }_2$ and ${\Psi }_4$, while ${\Psi }_2$ and ${\Psi }_3$ seem rather uncorrelated at LHC energies—such that the cosine factor does not vanish on average (Measurements of suitable multiparticle observables have been proposed to access those average cosine terms [2]). Nonetheless, we neglect those nonlinear terms in the following and focus on the first contribution on the right hand side of Equation (5), i.e., we approximate $v_{n,c}^{\mathrm{pair}}(\Delta \phi )\simeq \frac{1}{2}\left[v_n\left(a\right)+v_n\left(b\right)\right]cos(n\Delta \phi /2)$.

We now focus on the fluctuations of the single-particle flow coefficients $v_n$. These reflect fluctuations in the eccentricities ${ϵ}_n$ of the initial-state geometry. When the latter remain small, i.e., for not too peripheral collisions, $v_n$ and ${ϵ}_n$ for $n=2,3$ are almost linearly related $v_n\simeq {\kappa }_n{ϵ}_n$, as found both in fluid-dynamical [3,4,5] and in far-from-equilibrium transport [6] calculations. Accordingly, the fluctuations in ${ϵ}_n$ are linearly transferred into fluctuations of the final-state $v_n$. The probability distribution of the fluctuations of ${ϵ}_n$ for arbitrary n resp. $v_n$ for $n=2,3$ is to a very good approximation a power law distribution [7,8]

$$P_{ϵ}\left({ϵ}_n\right)=2_{}{\alpha }_{}{ϵ}_n{(1-{ϵ}_n^2)}^{\alpha -1}\mathrm{resp}.P_v\left(v_n\right)=\frac{2_{}\alpha }{{\kappa }_n}\frac{v_n}{{\kappa }_n}{\left(1-\frac{v_n^2}{{\kappa }_n^2}\right)}^{\alpha -1}$$

(6)

with $0\le {ϵ}_n\le 1$ resp. $0\le v_n\le {\kappa }_n$. Note that the fluctuations of $v_4$ may also be describable by a power law [9], although both ${ϵ}_2$ and ${ϵ}_4$ contribute. The only parameter in these distributions is the number $\alpha$, which depends on n. In general the power law distribution becomes sharper for higher values of $\alpha$. In order to pin down the value of this parameter, we performed Glauber Monte Carlo initial stage studies and fitted the power law distribution to the gained histograms for the values of the realized eccentricities ${ϵ}_n$.

Using Equation (5), without the terms from the sum—which is a reasonable assumption if we choose $n=3$ as we do now—and the probability distribution (6) for the single-particle triangular flow $v_3$, we can deduce the probability distribution for the pair flow coefficient $v_{3,c}^{\mathrm{pair}}(\Delta \phi )$. In the above sketched scenario—no two-particle correlation at play, power law distributions for $v_3\left(a\right)$ and $v_3\left(b\right)$—the fluctuations of $v_{3,c}^{\mathrm{pair}}$ are governed by the distribution

$$P\left(v_{3,c}^{\mathrm{pair}}\right)=\int d{v}_3\left(a\right)\int d{v}_3\left(b\right)P_v\left(v_3\left(a\right)\right)P_v{\left(v_3\left(b\right)\right)}_{}\delta \left(v_{3,c}^{pair}-\frac{\left[v_3\left(a\right)+v_3\left(b\right)\right]}{2}cos\frac{3\Delta \phi }{2}\right),$$

(7)

where the integrals run over the whole set of realizations of $v_3$ for particle a and particle b—here assumed to be totally independent. The delta distribution guarantees the functional dependence of the pair flow coefficient $v_{3,c}^{\mathrm{pair}}(\Delta \phi )$ on $v_3\left(a\right)$ and $v_3\left(b\right)$. As one can see, the probability distribution of the pair flow coefficients depends on the relative angle $\Delta \phi$ (The sine pair flow coefficient $v_{3,s}^{\mathrm{pair}}(\Delta \phi )$ shows a similar behaviour. Further details will be included in a forthcoming paper).

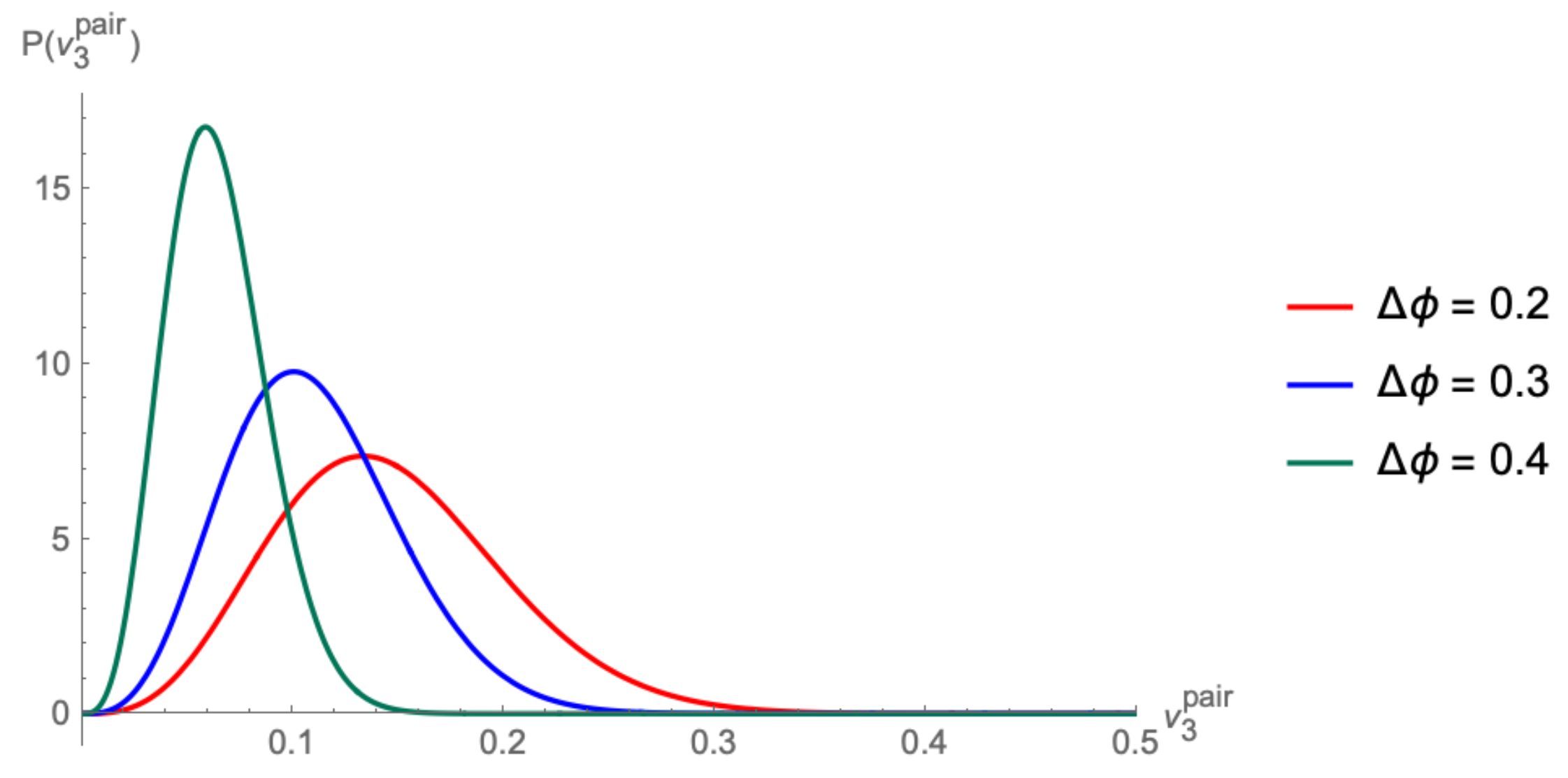
In Figure 1, we display the distribution (7) for different values of the relative angle $\Delta \phi$, using fitted values of $\alpha$.

One observes that the distributions are more peaked for larger values of the relative angle, whereas for small relative angles—when the cosine inside the delta distribution in Equation (7) approaches 1—the fluctuations in $v_n$ are strongly affecting the distribution of the pair flow coefficient.

3. Discussion

In these proceedings, we show how the single-particle flow coefficients $v_n$ and their fluctuations influence the pair flow coefficients $v_{n,c}^{\mathrm{pair}}$ and $v_{n,s}^{\mathrm{pair}}$, which are suitable observables to investigate the azimuthal dependence of two-particle distributions. We assumed that the two particles under study are uncorrelated, except through their individual “correlation” to the symmetry plane directions. In an actual experimental situation, the two particles may be correlated together due to other physical effects, so that what we considered may be viewed as a mere background to the genuine two-particle correlation. Disentangling the contribution of this fluctuating background from that of the signal, which might itself be fluctuating, will be a daunting task necessitating further studies, both semi-analytical and numerical.