Design and Optimization of Wideband Multimode Piezoelectric MEMS Vibration Energy Harvesters ^†

Abstract

To enlarge operating frequency bandwidth of the multimode energy harvesters, nonlinearity characteristics has to be well presented by the system configuration. Therefore, the conventional optimization techniques, which are solely based on human observation, are highly difficult and somehow impossible. In this paper we propose an efficient optimization technique for automating the design of nonlinear piezoelectric MEMS energy harvesters based on Genetic Algorithm (GA) with minimum human efforts. In this regard, a MEMS piezoelectric harvester with capability of operating at multimode is proposed and a GA-based optimization methodology is utilized to shift its operational modes close to each other by optimizing device physical aspects. The experiments on post-optimization resonant frequencies show that our proposed optimization methodology is able to reduce the resonant frequencies by 13%, 10% and 9.5% for the first, second and third modes, respectively. In addition, the numerical simulation shows that our optimized energy harvester with a total chip area of 16-mm² is able to maximally generate 655 mV, 80 mV and 572 mV at the first (153 Hz), second (168 Hz) and third (219 Hz) modes, respectively under 1 g vibration.

1. Introduction

In the MEMS scale, the kinetic energy of vibrations can be converted to electricity by electrostatic-, electromagnetic- and piezoelectric-techniques [1]. Each technique has its own advantages as well as drawbacks. For instance, the electrostatic-based technique is capable of producing a tiny energy harvester. However, the requirement of external bias voltage or electret material for polarization of capacitors’ plates makes this method less suitable for an energy harvester [2]. The performance of the electromagnetic energy harvesters is dependent on magnetic field strength. So utilizing a large permanent magnet may degrade the device portability level [3]. In contrast, the piezoelectric-based technique does not demand an external bias voltage. Moreover, the piezoelectric-based technique has been demonstrated with higher energy conversion efficiency in comparison to the other methods [4]. In addition to these advantages, the piezoelectric material (e.g., PZT, ZnO, AlN and etc.) can be deposited by regular MEMS fabrication process. Consequently, the piezoelectric-based method has been identified as one of the most promising techniques for providing the MEMS vibration energy harvesters.

In the previous studies, most of the applicable structures for the MEMS piezoelectric harvesters are a beam with clamped—free end boundary. Piezoelectric materials can be deposited on one or two sides of the beam (i.e., unimorph or bimorph, respectively). However, this type of harvesters has so narrow operating bandwidth that variation in the ambient vibration frequency often makes them less useful. To enlarge operational frequency bandwidth, Liu et al. [5] proposed to utilize several piezoelectric cantilevers with different resonant frequencies as an array. Since in the proposed structure only one cantilever operates at one time, the device power density is very low. Tang et al. [6] presented another feasible method to widen operational frequency of the MEMS piezoelectric harvesters, by using bi-stable mechanism. In this way, a two-stage harvester can be actuated by magnetic field and piezoelectric mechanism. Although the harvester operating frequency bandwidth can be significantly increased, necessity of micro-assembling magnets along the cantilevers enlarges the device size and incurs difficulties in fabrication. As a result, in this study we are motivated to develop a MEMS piezoelectric energy harvester with capability of operating at multimode without using permanent magnets. Since our proposed harvester has nonlinear behavior due to its multi-degree of freedom, accurate estimation of its performance is somehow impossible. To save human laborious design efforts, we present an optimization method based on genetic algorithm (GA), which can serve as an effective way for automated design and optimization of the nonlinear energy harvesters.

This paper is organized as follows. A short introduction to the MEMS vibration-based energy harvesters is presented in this section. In Section 2, the proposed wideband energy harvester structure is discussed. Then the GA-based optimization methodology is described in Section 3. The numerical simulation results and discussions are provided in Section 4. Finally the conclusion is made in Section 5.

2. Multimode MEMS Piezoelectric Harvester

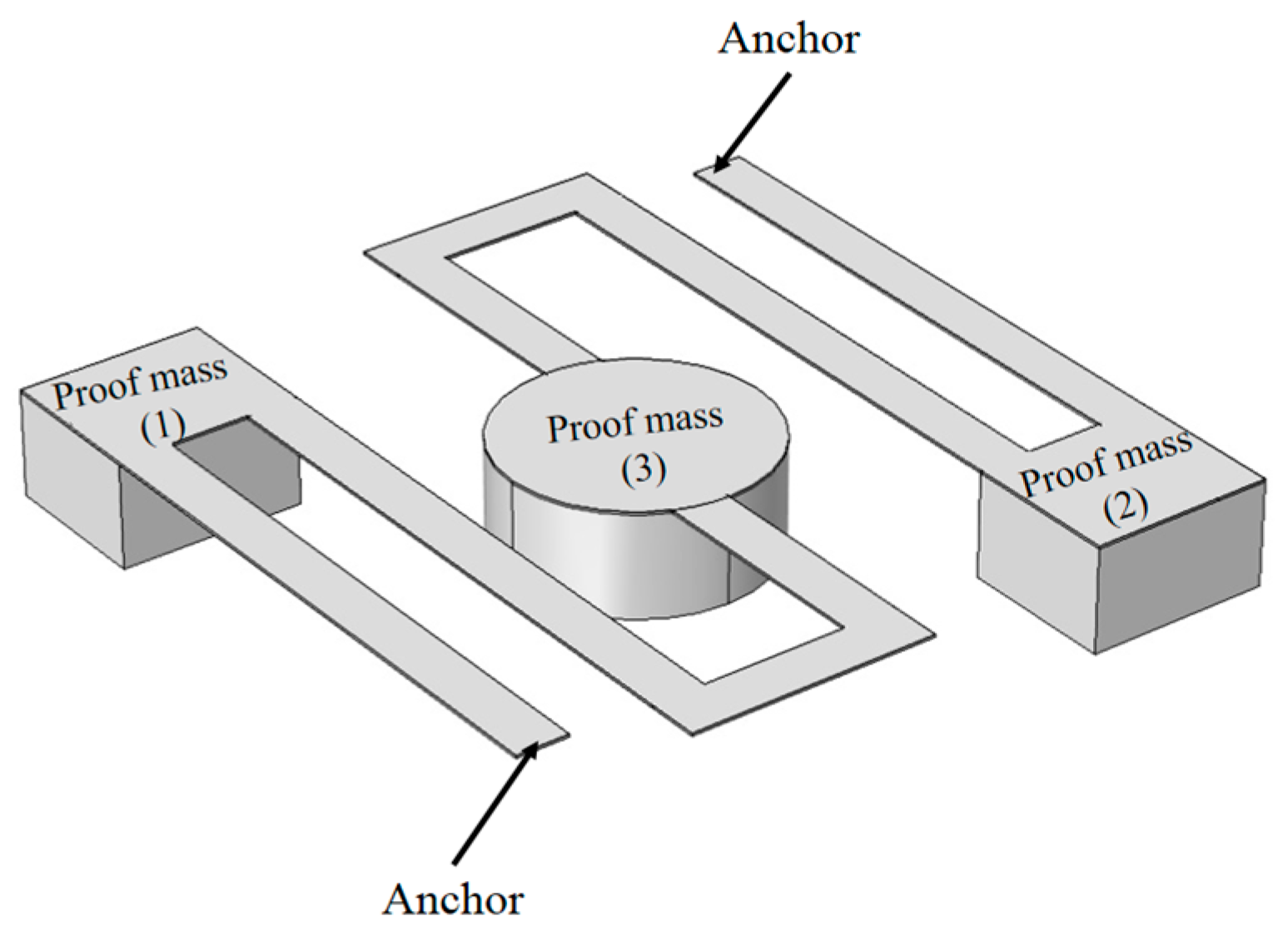
The schematic of the proposed multimode MEMS piezoelectric harvester is illustrated in Figure 1. This energy harvester is anchored on two sides. In the other words, it can be overviewed as a doubly clamped cantilever. Since this proposed energy harvester has a symmetric structure, multi-degree of freedom provides nonlinearity behavior during the oscillation of the device. In order to enlarge the device efficiency and reduce its operating frequencies, we have utilized 3 proof masses at different locations, which are numbered sequentially. Consequently, these suspended proof masses, which are bonded to the cantilever, increase load force as well as device mass for frequency reduction.

3. GA-Based Optimization Methodology

The genetic algorithm (GA) is an evolutionary computation method for optimizing complex problems. In this way, a group of variables are defined as optimizeable parameters and GA strives to generate a set of random numbers for these parameters. By using the defined fitness function(s), one set of proper parameter values, which can offer extreme amount of the fitness function, is chosen as the optimum solution [7]. Since the generation of random numbers is performed in a multidimensional manner, our proposed optimization method, unlike any manual optimization endeavors, can statistically converge to the global optimum rather than being entrapped into local optima.

In the following section, the GA performance on geometry optimization of the proposed MEMS energy harvester described in the previous section for improving its operating frequencies will be discussed.

4. Numerical Simulation Results and Discussion

In the first step, operating frequency of our proposed MEMS piezoelectric harvester was computed by using finite element modeling (FEM). In this study, we used COMSOL Multiphysics (Version 5.2a), a commercial FEM simulator. In order to implement the proposed GA-based optimization methodology, we utilized MATLAB GA toolbox (Version 2014). By applying a single-objective fitness function, we optimized the sizes of the proof masses to reduce the operating resonant frequencies. The required fitness function of GA was provided by COMSOL, which means it was connected to MATLAB by using LiveLinke module. Therefore, the effects of the generated random values on resonant frequency during iterative calling by the algorithm are evaluated by FEM simulation.

In

Table 1. The multimode resonant frequencies for the un-optimized and the optimized proof masses.

Method	Mass 1 (μm)	Mass 2 (μm)	Mass 3 (μm)	f1 (Hz)	f2 (Hz)	f3 (Hz)	Time (min)
Range	(250–550)	(250–550)	(450–850)	-	-	-	-
Un-Optimized	350	350	530	177	187	242	-
Optimized by COMSOL	345	251	724	151	194	263	90
Optimized by GA	443	442	715	153	168	219	68

By using COMSOL optimization module and our proposed optimization method.

, the measured amounts of the first, second and third mode resonant frequencies for un-optimized MEMS piezoelectric energy harvester and optimized one are listed, respectively. In addition, we compared our proposed optimization methodology effectiveness with COMSOL optimization module, which is commercially available for MEMS structural optimization. As reflected in Table 1, it is obvious that the optimized geometry by using our optimization methodology proposed in this paper can contribute to lower resonant frequencies than that from the COMSOL optimization module. It is worth noting that our proposed method is more efficient than the commercial one in terms of runtime. It can be highlighted the proposed optimization methodology is capable of reducing resonant frequencies by 13%, 10% and 9.5% for the first, second and third modes in reference to the un-optimized harvester frequencies, respectively.

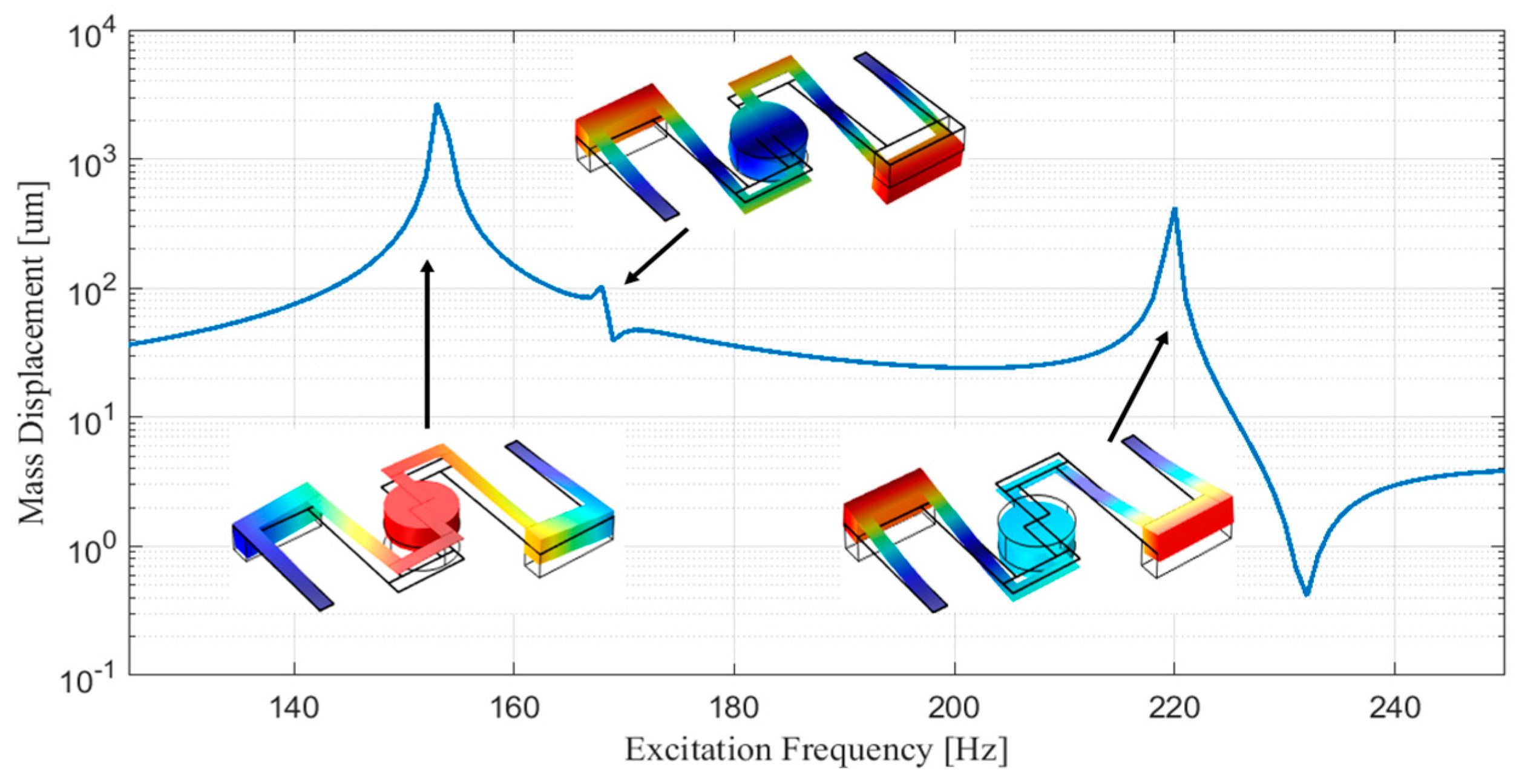
Frequency spectrum of the optimized harvester with isotropic materials for silicon beam and piezoelectric film was computed and displayed in Figure 2. Furthermore, the shape of the proposed wideband energy harvester at each mode is presented. One can observe that the energy harvester at each mode shows a specific shape, which helps to drive the harvester at multiple modes to form the wideband aspect.

Finally the performance of the optimized energy harvester in terms of harvested voltage was studied. The magnitude of the harvested voltage at each mode under a sinusoidal oscillation of vibration with amplitude of 1 g (1 g = 9.8 m/s²) was measured. It is observed that the optimized energy harvester could maximally generate peak voltage of 655 mV, 80 mV and 572 mV at the first (153 Hz), second (168 Hz) and third (219 Hz) modes, respectively, which are larger than the counterparts from the un-optimized harvester and the COMSOL optimization module output.

5. Conclusions

In this paper we proposed a wideband MEMS piezoelectric energy harvester for operating at multiple modes. Due to the strong nonlinearity for this type of the harvesters, the conventional optimization techniques based on human plain observation exhibit less efficiency. Therefore, we introduced a GA-based geometry optimization method, which can be conducted with minimum human efforts. The numerical FEM simulation results clearly demonstrate that our proposed method is able to considerably optimize the operating frequencies. The optimized energy harvesters is able to generate peak voltage of 655 mV, 80 mV and 572 mV at the first, second and third modes, respectively, under 1 g vibration.