Abstract
Wearable sensor technologies are a key component in the design of applications for human activity recognition, in areas like healthcare, sports and safety. In this paper, we present an iterative learning method to classify human locomotion activities extracted from the Opportunity dataset by implementing a data-driven architecture. Data collected by twelve 3D acceleration sensors and seven inertial measurement units are de-noised using a wavelet filter, prior to the extraction of statistical parameters of kinematical features, such as Principal Components Analysis and Singular Value Decomposition of roll, pitch, yaw and the norm of the axial components. A novel approach is proposed to minimize the number of samples required to classify walk, stand, lie and sit human locomotion activities based on these features. The methodology consists in an iterative extraction of the best candidates for building the training dataset. The best training candidates are selected when the Euclidean distance between an input data and its cluster’s centroid is larger than the mean plus the standard deviation of all Euclidean distances between all input data and their corresponding clusters. The resulting datasets are then used to train an SVM multi-class classifier that produces the lowest prediction error. The learning method presented in this paper ensures a high level of robustness to variations in the quality of input data while only using a much lower number of training samples and therefore a much shorter training time, which is an important aspect given the large size of the dataset.
1. Introduction
Wearable sensor technologies are gaining interest in research communities due to the use of significantly miniaturized electronic components, with low power consumption, which makes them ideal for applications in human activity recognition for both indoor and outdoor environments. These applications allow users to achieve a natural execution of any physical activity, while providing good results in multiple practical applications, such as health rehabilitation, respiratory and muscular activity assessment, sports and safety applications [1]. However, in practical situations, collected data are affected by several factors related to sensor data alignment, data losses and noise, among other experimental constrains, all deteriorating their quality [2]. Also, the non-ergodicity of the acquisition process, especially when processing signals from acceleration sensors, will result in a poor learning performance [3] in applications involving multi-class classification [4]. The problems become even more complex if the multi-class classification process is applied on high dimensionality data vectors. Considering these restrictions prevalent in multimodal sensor data fusion [3], which is the case in the study, reported in this paper, feature extraction becomes a critical component for finding the multi-variable correlations that allow the classifier to improve the model precision reflected by a low misclassification rate.
In this paper, we present a new method for classifying human locomotion activities (e.g., walk, stand, lie and sit) by implementing a data-driven architecture based on an iterative learning framework. The proposed solution optimizes the model performance by choosing the best training dataset for non-linear multi-class classification that makes use of an SVM classifier, while also reducing the computational load. We aim to show that by appropriately choosing our data samples for the training of this multi-class classifier, we can achieve close results to the current approaches in the literature, while using only a fraction of the data and improving significantly the computation time. The article is organized as follows: Section 2 presents our method. Section 3 shows relevant results, and Section 4 discusses the conclusions.
2. Iterative Learning Method for Classifying Human Locomotion
The work in this paper is based on data acquired by body–worn sensors, and extracted from the Opportunity dataset [5]. The body-worn sensors are twelve 3D-acceleration customized sensors [6] and seven inertial measurement units—IMUs (Xsens MT9). The dataset has a total of 58 dimensions including the time stamp. Each device senses the acceleration in the 3 perpendicular axes, recording the acceleration values at a sampling rate of 30 Hz. All records are labeled according to four primitive classes: walk, lie, sit and stand. The signal acquisition protocol is performed under a pre-established scenario with six experimental sessions (or runs), performed independently by four users. The extracted dataset contains a total of 869,387 samples, which are distributed as follows: 234,661 samples for user 1; 225,183 samples for user 2; 216,869 samples for user 3, and 192,674 samples for user 4. The goal of is to extract from these data the best training samples that enable the classification of the locomotion activity of the users independently.
2.1. Data Pre-Processing
The data pre-processing phase consists of two steps. First, we proceed with the exclusion of values affected by data losses and random noise, issues that are very common in wireless acceleration sensors. In the dataset we use, roughly 30% of the data contains such values. In order to deal with the problem of missing data, we fused all readings produced by each sensor, for each user and each experiment, to work exclusively from a data-driven perspective, as explained in the following sections. The aim of the second step is to de-noise the raw data.
2.1.1. Wavelet Filtering
In order to efficiently de-noise raw data, we include a mechanism that guarantees that the resulting classification model is not biased due to the quality of the input data [7]. In general, the acceleration sensors are influenced by several noise sources, such as electrical noise induced by the electronics [8], or noise produced by the wireless communication processes, resulting from the propagation phenomenon and causing distortion in the transmitted signal. The noise present in the acceleration sensor measurements has commonly a flat spectrum. This means that the noise is present in all frequency components. This constitutes a challenge for the use of traditional filtering methods, which by removing sharp features, can introduce distortions in the resulting signal. Decomposition of the noisy signal into wavelets [9] will eliminate small coefficients, commonly associated with the noise, by zeroing them, while concentrating the signal in a few large-magnitude wavelet coefficients.
2.1.2. Feature Extraction and Selection
After filtering the raw data, we proceed with the feature extraction and selection process. The aim is to retrieve a set of data with high correlation, allowing us to extract the best candidates for the training dataset [10]. This process focuses on the extraction of kinematics features, such as roll, pitch, yaw (RPY), and the norm of the axial components produced by each of the body-worn sensors. Our first feature set is based on the signal magnitude vector (SMV). At each time instance j, an acceleration sensor k produces a 3D vector, consisting of acceleration values along a system of orthogonal axes . For each sensor, we can retrieve the single magnitude vector . A second feature set is related to roll, pitch and yaw (RPY), calculated as follows:
Finally, we build a matrix with all axial components produced by all sensors under observation:
The last matrix has components, where n is the number of samples in each experiment for sensors in dimensions. To deal with the absence of some values, we use principal component analysis (PCA) and singular value decomposition (SVD). PCA provides a mechanism to reduce dimensionality, while SVD provides a convenient way to extract the most meaningful data. Combining these techniques, we find data dependency while removing redundancy. PCA and SVD ensure the preservation of the nature of the resulting data structures on each feature category. When applying PCA, each feature category is reduced to two principal components (Figure 1a). Similarly, when SVD is applied, each feature category is reduced to the two first SVD dimensions, as shown in Equation (3). The new target function is represented as follows:
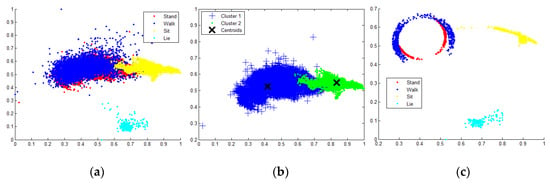
Figure 1.
(a) PCA is applied to (data distribution corresponds to the first and second principal components); (b) Classes are extracted in pairs (, centroids are extracted and Euclidean distances are calculated according to step 6; and (c) Training candidates are produced by the selection algorithm.
We are therefore reducing our analysis to a function with three attributes () and two mathematical methods, PCA and SVD.
2.2. Learning Architecture
Our learning framework aims to classify human activities using a single multi-class SVM classifier (LibSVM version 3.20 [11]). To achieve this, we must deal with two data constrains: (1) the large size of the experimental datasets containing in many cases overlapping class members and high data density; and (2) the non-ergodicity of the recorded signals demonstrated by the fact that we were not able to find temporal patterns in the dataset. In order to improve the classification accuracy, while reducing the processing time required, features produced by Equation (3) are grouped pairwise to cover all the possible combinations. The candidates for the training dataset are then determined by measuring the Euclidean distance between each class member and the centroids of each distribution of (). If the resulting distance is larger than the mean plus the standard deviation of all resulting Euclidean distances, then the class member is considered a candidate for the training set. This process leads to the creation of support vectors, which generate the optimal separation plans to classify the remaining data with only a fraction of the total data presented for each user experiment. The goal is to build a robust classification model, which will not be affected by the quality of the input data [12].
2.3. Training Data Selection
The following procedure summarizes the process for the extraction of the training dataset (for any user and any experiment):
- Select a user.
- Select a user experiment.
- Extract two features () from the experiment.
- Extract all classes from ().
- Select a pair of classes ( (i.e., a one-versus-all methodology is used) and extract their corresponding centroids.
- Extract the Euclidean distance between each class member () and the centroid of the class (. Store the results in a vector of distances :where n and m are the classes of (), is a class member and is the opposite centroid with respect to the discriminating hyperplane of the class member under evaluation (Figure 1b).
- If the resulting Euclidean distance vector satisfies condition (5), then the class member is a candidate for the training dataset.where and are the mean and standard deviation of the Euclidean distance vector . The candidate is stored in a vector of candidates BoC() (Figure 1c).
- Repeat steps 3 to 7 until all classes in () have been evaluated.
2.4. Model Selection
Once the best training dataset BoC() has been identified, we proceed with the selection of the best classification model using a multi-class SVM classifier with an RBF kernel. Since we have more than 2 classes, we follow the strategy one-versus-all. The problem of model selection is reduced to finding the best combination of parameters cost, c and γ extracted in a 5-fold cross validation process, in which the values of c and γ are chosen according to a grid of values, i.e., (). The reason we used this grid is to compensate for the behavior of c and γ. When c is large the classifier presents low bias and high variance. For small values of c the classifier presents high bias and low variance. A similar situation is found with γ. For large values of γ the classifier presents high bias and low variance and for small values of γ the classifier presents low bias and high variance. The best model produced by the combination of c and γ in a 5-fold cross-validation will achieve the lowest misclassification rate. This model is then used to predict the labels on the testing dataset. Once the classification rate is determined, the algorithm stores the accuracy values, the features (), c and γ and the size of the training sample BoC() and repeats the process until all combinations of are exhausted.
3. Experimental Results
The proposed process is evaluated over three experimental scenarios and the results are presented in Table 1, Table 2 and Table 3. We compare our method with a scenario in which the training dataset is randomly selected and its size corresponds to 80% of total of data of each user experiment, common practice when 5-fold cross-validation is performed. These last results are compared with our proposed method and presented in Table 4. We use two measures to validate our results, namely the prediction accuracy (Acc) and the size (as percentage of the total dataset) of the training dataset that is used (TS):

Table 1.
Classification performance obtained from IMU sensors.

Table 2.
Classification performance obtained from 3D acceleration sensors.

Table 3.
Classification performance obtained from IMU and 3D acceleration sensors.

Table 4.
Accuracy comparison.
It is important to state that the values for Acc and TS depend on the size of the user dataset and the resulting vector in Equation (5). These values are changing with the number of measurements in each user experiment. Table 1 presents the results when using only data obtained from the IMU sensors, Table 2 shows the values for Acc and TS when using data obtained from the 3D acceleration sensors and Table 3 when using data obtained from the 3D acceleration sensors and IMU devices in three experiments.
These results are compared in Table 4, that shows the average accuracy when using two training dataset selection strategies, one with a limited number of training samples (first three columns) and the other one with a large number of training samples (i.e., 80% in last three columns). One can observe that using on average of 7.33% of the dataset for training, the performance achieved is only about 7.28% under the performance obtained when the classifier processes a high number of training samples.
The use of a smaller training set leads as well to an important decrease in the computation time. The average processing time per user experiment is roughly 35 min when using the strategy of training with 80% of the dataset, on a single processor Intel64 7 at 3 KHz, 6 Gb RAM memory. It is worth mentioning that the use of the iterative process leads to a significant reduction in the average time for processing an experiment to about 5 minutes that represents less than 15% of the time required when 80% of the dataset is used for training.
4. Conclusions
In this paper, we proposed a novel iterative learning process to reduce the number of samples and subsequently the processing time for the classification of measurements from wearable sensors. The challenges related to the large percentage of missing data and the noise affecting the measurements were successfully dealt with by the use of data fusion and of a robust filtering stage based on wavelets. The inclusion of a mechanism for the selection of the training dataset allows us to work with only a fraction of the total dataset for the SVM multi-class training process. The minimization of the number of samples is an important contribution that allows to deal efficiently with large data sets as those explored in this paper.
Author Contributions
Juan Carlos Dávila conceived and designed the proposed framework and wrote the paper; Ana-Maria Cretu assessed and corrected the content of the paper, analyzed data results and suggested methodologies to improve classification results. Marek Zaremba reviewed the paper, validating the methodology and the final content of paper. He also suggested technical approaches to deal with the problem of noise reduction.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Patel, S.; Park, H.; Bonato, P.; Chan, L.; Rodgers, M. A review of wearable sensors and systems with application in rehabilitation. J. Neuroeng. Rehabil. 2012, 9, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Chavarriaga, R.; Sagha, H.; Calatroni, A.; Digumarti, S.T.; Tröster, G.; Millán, J.D.R.; Roggen, D. The Opportunity challenge: A benchmark database for on-body sensor-based activity recognition. Pattern Recognit. Lett. 2013, 34, 2033–2042. [Google Scholar] [CrossRef]
- Khaleghi, B.; Khamis, A.; Karray, F.O.; Razavi, S.N. Multisensor data fusion: A review of the state-of-the-art. Inf. Fusion 2013, 14, 28–44. [Google Scholar] [CrossRef]
- Qian, H.; Mao, Y.; Xiang, W.; Wang, Z. Recognition of human activities using SVM multi-class classifier. Pattern Recognit. Lett. 2010, 31, 100–111. [Google Scholar] [CrossRef]
- Activity Recognition Challenge. Available online: http://opportunity-project.eu/challenge (accessed on 10 October 2016).
- Roggen, D.; Bächlin, M.; Schumm, J.; Holleczek, T.; Lombriser, C.; Tröster, G.; Widmer, L.; Majoe, D.; Gutknecht, J. An educational and research kit for activity and context recognition from on-body sensors. In Proceedings of the 2010 International Conference on Body Sensor Networks (BSN), IEEE, Singapore, 7–9 June 2010; pp. 277–282. [Google Scholar]
- Figo, D.; Diniz, P.C.; Ferreira, D.R.; Cardoso, J.M.P. Preprocessing techniques for context recognition from accelerometer data. Pers. Ubiquitous Comput. 2010, 14, 645–662. [Google Scholar] [CrossRef]
- Levinzon, F. Fundamental Noise Limit of an IEPE Accelerometer. In Piezoelectric Accelerometers with Integral Electronics; Springer International Publishing: Cham, Switzerland, 2015; pp. 107–116. [Google Scholar]
- Misiti, M.; Misiti, Y.; Oppenheim, G.; Poggi, J.-M. Guided Tour from Wavelet and Their Applications; Wiley: Hoboken, NJ, USA, 2007; pp. 1–27. [Google Scholar]
- Zhao, M.; Fu, C.; Ji, L.; Tang, K.; Zhou, M. Feature selection and parameter optimization for support vector machines: A new approach based on genetic algorithm with feature chromosomes. Expert Syst. Appl. 2011, 38, 5197–5204. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM—A Library for Support Vector Machines. Available online: http://www.csie.ntu.edu.tw/~cjlin/libsvm/ (accessed on 10 October 2016).
- Verbiesta, N.; Derrac, J.; Gent, C.C.U.; Garcia, S.; Herrera, F. Evolutionary wrapper approaches for training set selection as preprocessing mechanism for support vector machines: Experimental evaluation and support vector analysis. Appl. Soft Comput. 2016, 38, 10–22. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).