1. Introduction
In recent decades, megatrends like ubiquitous and pervasive computing or the Internet of Things (IoT) have supported considerable research and development efforts with the aim to provide everyday objects with some sort of smartness [
1]. Initially, the basis of these efforts has been the attachment or external application of sensors and later sensor and electronic systems, today there is a growing trend towards material integration [
2]. While many efforts in this direction have concentrated on sensing to connect the envisaged smart object to its environment [
3,
4,
5,
6], there is a growing trend to endow it with adaptivity on material level, too [
7,
8,
9]. The present study investigates autonomous control concepts for such smart adaptive materials and structures. The motivation behind this study is primarily lightweight design, which is a need specifically in transport applications [
10]. The fundamental hypothesis in this respect is that today, we are neglecting a vast potential for weight reduction due to the fact that established production methods provide us with material and structural solutions that for practical reasons have to be optimized for a limited number of design load cases. For many others, we are thus overdimensioning these structures.
Specifically structures that are prone to failure not through static overloading, but through fatigue and thus accumulation of damage over an extended period of time must appear to lend themselves easily to the suggested dynamic optimization approach: A controlled redistribution of loads within the structure could relieve critical areas at least under less critical loading conditions and thus extend their fatigue life based on individual, component-specific rather than generalized loads. Similarly, if the material-inherent control system was capable of damage detection and localization, it could decouple already damaged regions from internal loads e.g., by creating a cocoon of higher stiffness volume elements around them.
In the following sections, the basic structure of the envisaged control system will be described and justified, the ensuing research challenges will be identified and discussed, and an FEM simulation based virtual test environment will be proposed which will allow to evaluate main aspects of the aforementioned control concept.
2. Control Concept Outline and Background
Techniques for the optimization of structures for specific load cases are typically based on individual, static load cases. Examples of this kind include shape and topology optimization. In their fundamental form, these techniques only address homogeneous materials. In contrast, recently specific new approaches have emerged that optimally distribute different materials within a given structure. An early example of such approaches is the so-called Multi-Phase Topology Optimization (MPTO) originally developed by Andreas Burblies of Fraunhofer IFAM [
11]. Originally, this approach was developed to suggest optimum foam structures by distributing pre-defined material fractions having different densities and thus different Young’s moduli over the part volume. The principle behind the technique is an exchange of volume with the aim of minimizing total strain energy [
11]. Recently, MPTO has also been adopted to define load-dependent optimum geometries of reinforcement structures within a matrix material, i. e. assuming just two different materials rather than several levels of porosity.
For our own concept, we derive from this virtual example the information that there are basically simple mechanisms which allow tailoring internal stiffness distributions to an overall optimization target, provided that sufficient knowledge about the momentary internal state of the structure is available on the level of individual cells, which constitute the basic volume elements both in terms of sensing and property change: The MPTO approach gathers this information from FEM simulations, which are re-iterated whenever a change of stiffness distributions has been affected. In contrast, for the envisaged adaptive materials, equivalent information must be obtained via sensor data, while for pushing property distributions towards an optimum, communication between the different cells is mandatory to decide on which changes to effect.
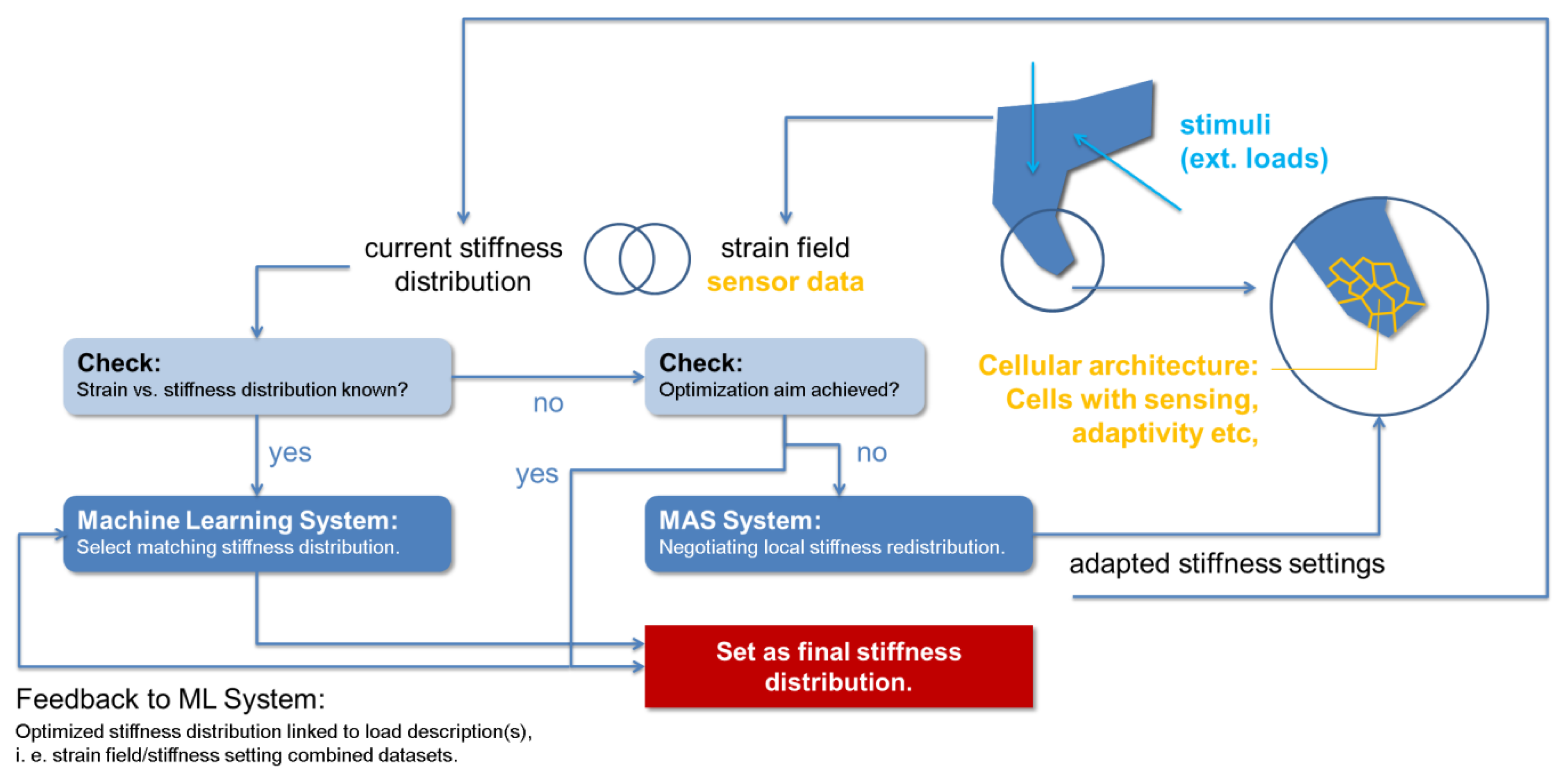
Figure 1 illustrates the main functionalities of the control concept and their interaction, which like in MPTO follows an iterative approach meant to converge towards the optimization target. Starting point is the current stiffness distribution. Subjecting the component in question to external loads will result in state changes in the individual cells, e.g., described by a strain field. If the part has encountered this same load before, and if this fact is recognized internally by matching the current strain distribution with the response represented by the strain field, an associated stiffness distribution can be selected directly. Doing so is the task of a machine learning system which maintains links between stiffness and e.g., strain distributions on the one and load cases on the other side: Any new load case encountered will be classified accordingly via an incremental learning strategy to make it available in future for direct stiffness distribution setting. For unknown load cases and the case that the present stiffness distribution does not reflect the optimization target, a Multi-Agent System (MAS) is envisaged which will negotiate the re-setting of properties between the material’s cells, making use of changes in sensor data as feedback to either confirm or discard the changes effected in each iteration.
Figure 2 illustrates the interaction of the software components in more detail. The MAS system itself will be based on previous studies addressing material-integrated intelligent systems aimed at structural monitoring rather than control [
12,
13,
14]. Testing and competitive evaluation of candidate algorithms for this task will be a major aspect of further research in this field. Of similar importance is the question in how far distributed, localized decision-making can approximate a global optimum, and thus whether communication and algorithms on global scale might be needed in addition to the local ones. Prior to settingup a physical structure, such issues will be evaluated using the virtual test environment described in the following section.
3. Virtual Test Environment
Physical realization of an adaptive structure at the envisage level of granularity is currently hampered by the availability of suitable materials and sufficiently miniaturized electronic sensing, actuation/stimulation and control systems. As an intermediate stage, physical testing of control strategies may be based on lower resolution systems that mimick the expected material behavior on structural level. Studies of this kind have e.g., performed by McEvoy and Correll [
7,
8,
9]. At the same time, there is a growing number of studies which look at material-level mechanisms that can lead to a reversible change in the stiffness of a given structural material—many of the available examples in this respect are linked to inspirations from the living world. Recently, Saavreda Flores et al. have collected different mechanisms of this kind, including [
15]
change in moisture levels (e.g., found in wood cells)
temperature change, effective e.g., via transgression of glass transition temperature (e.g., thermoplastic polymers, natural example spider silk)
chemically induced change of nanofiber- and nanofiber-matrix interactions in nanocomposites (polymer-cellulose nanocompsites)
sacrificial bonds in molecular cross links between polymer chains (proteins)
Among the effects practically evaluated in experiments targeting adaptive stiffness materials is e.g., the thermal effect, as it is rather easy to realize specifically on a larger, structural scale—however, despite the possibility of such model experiments, and even with true “robotic materials” [
9] at hand, simulation-based verification and optimization of control algorithms remains a necessity—thus there is a twofold need for a virtual environment that facilitates these tasks. Our own approach in this respect is based on replacing the physical structure with a simulation tool which accepts a description of the stiffness distribution as input parameter and hands back the local, element-level load data to the MAS system, which in turn emulates communication as it would appear in the physical structure. In a first approach, the structural simulation part will be implemented through FEM simulation using Abaqus™ as the associated tool.
4. Conclusions
In this text, we have presented a general, multi-level concept for a control mechanism that would allow a mechanically loaded structure to adapt its property distribution to external mechanical loads. The prerequisite is that this structure is composed of a material that in turn consists of several mechanically connected cells which can for one thing sense mechanical loads acting on them through reactions like mechanical strain, and are besides capable of adapting their mechanical properties—and among these most importantly their stiffness—in a controlled manner.
Future work will start with a virtual evaluation of control algorithms which utilizes the simulation-based test environment sketched in the present text. This evaluation will consider aspects like reliability, robustness and speed and compare different generalized optimization targets, such as achieiving a minimum of internal elastic energy, limiting peak stress levels or decoupling damage sites from the surrounding material. In parallel, efforts will be made to identify suitable material systems which allow practical evaluation of the results in an experimental setup. First studies of this kind will most likely be conducted on a structural rather than a material level.