Fractional-Order Constitutive Modeling of Shear Creep Damage in Carbonaceous Mud Shale: Experimental Verification of Acoustic Emission Ringing Count Rate Analysis
Abstract
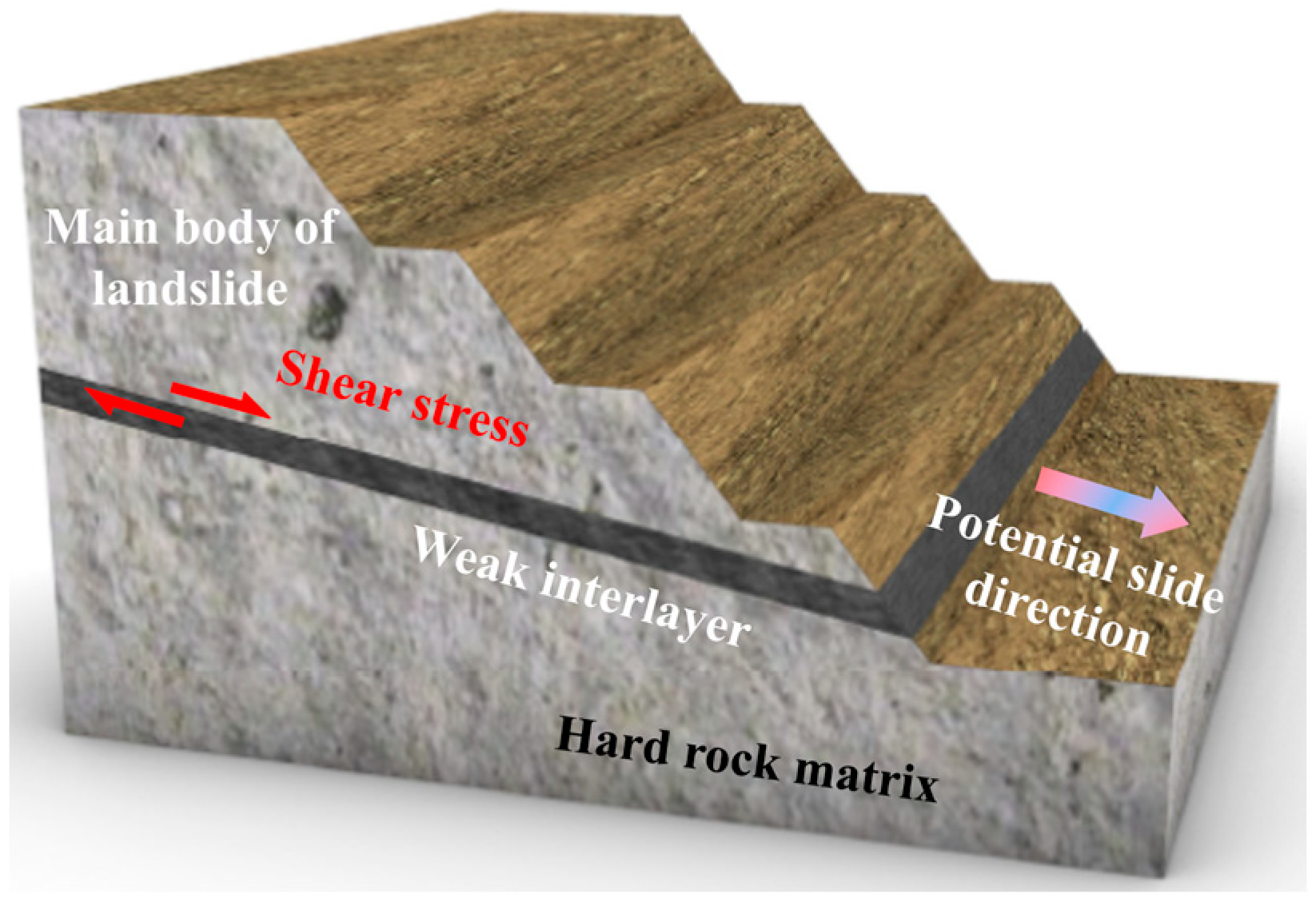
1. Introduction
2. Experimental Methods
2.1. Samples and Experimental Instruments
2.2. Experimental Scheme
3. Experimental Results and Discussion
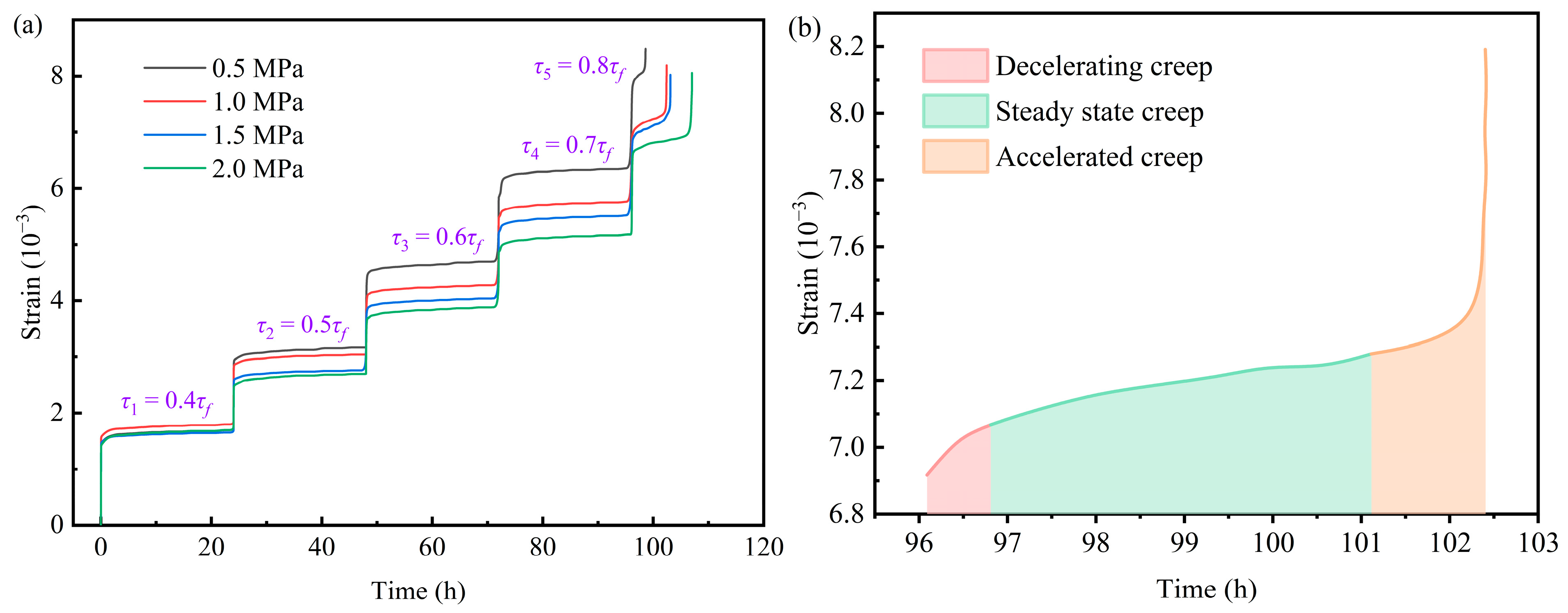
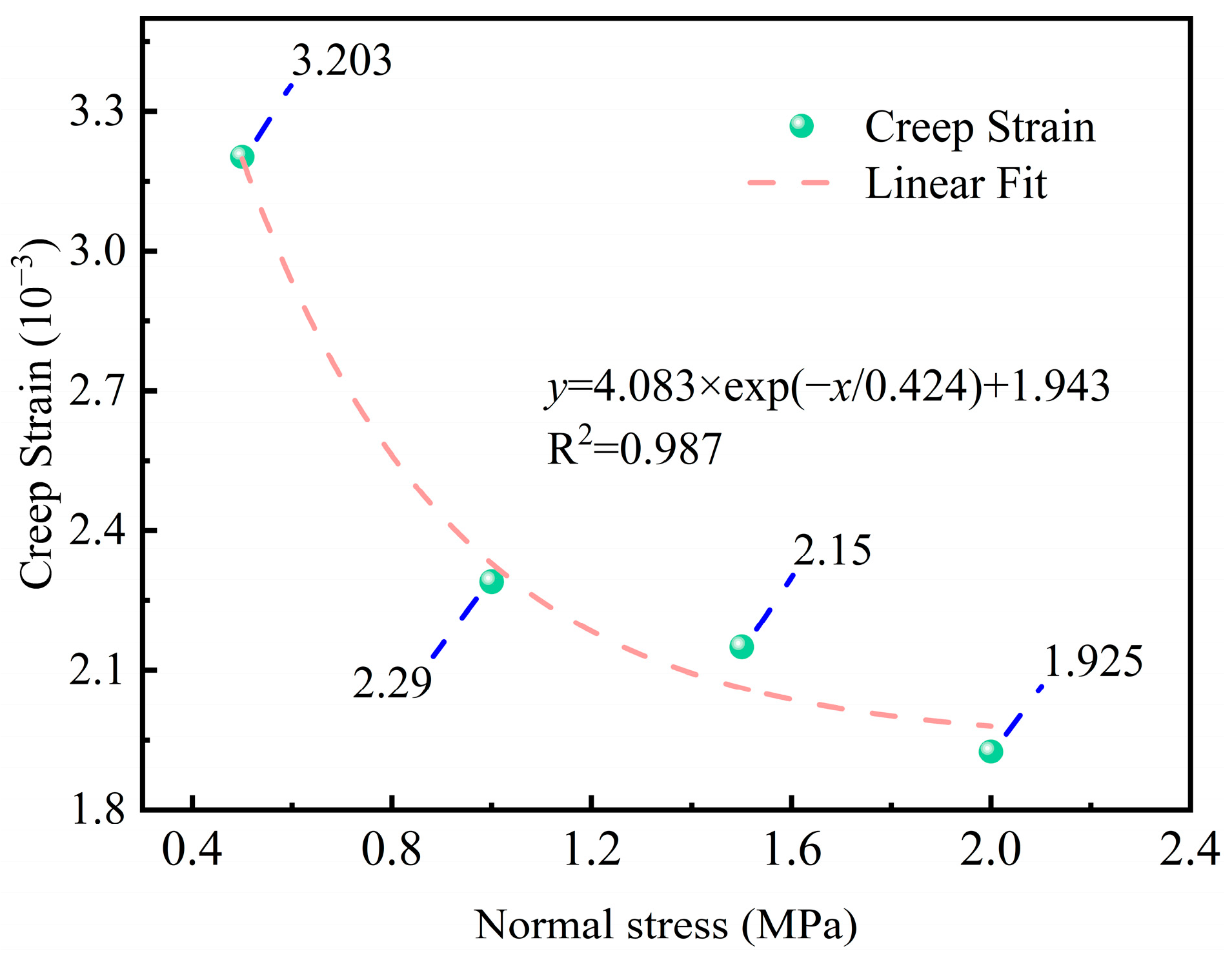
3.1. Shear Creep Curves of Carbonaceous Mud Shale
3.1.1. Shear Creep Deformation
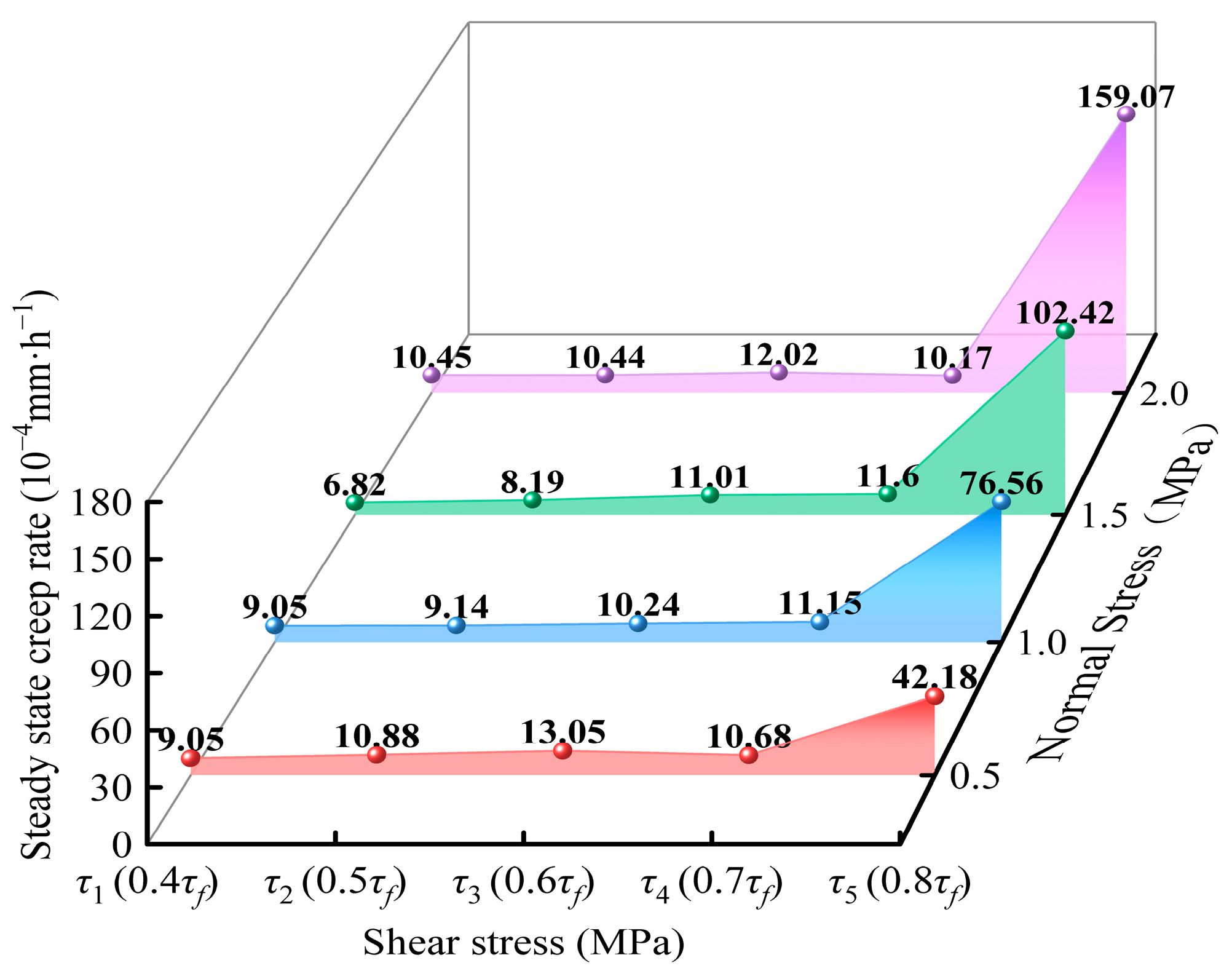
3.1.2. Steady State Creep Rate
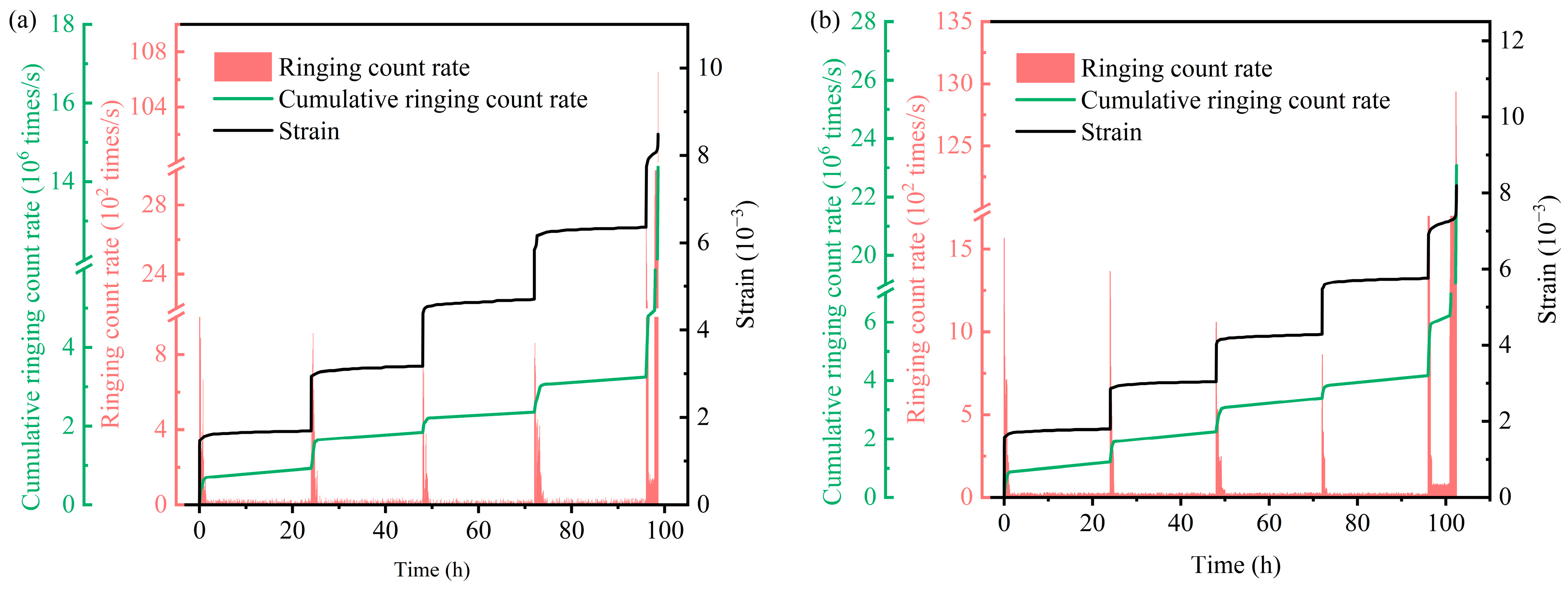
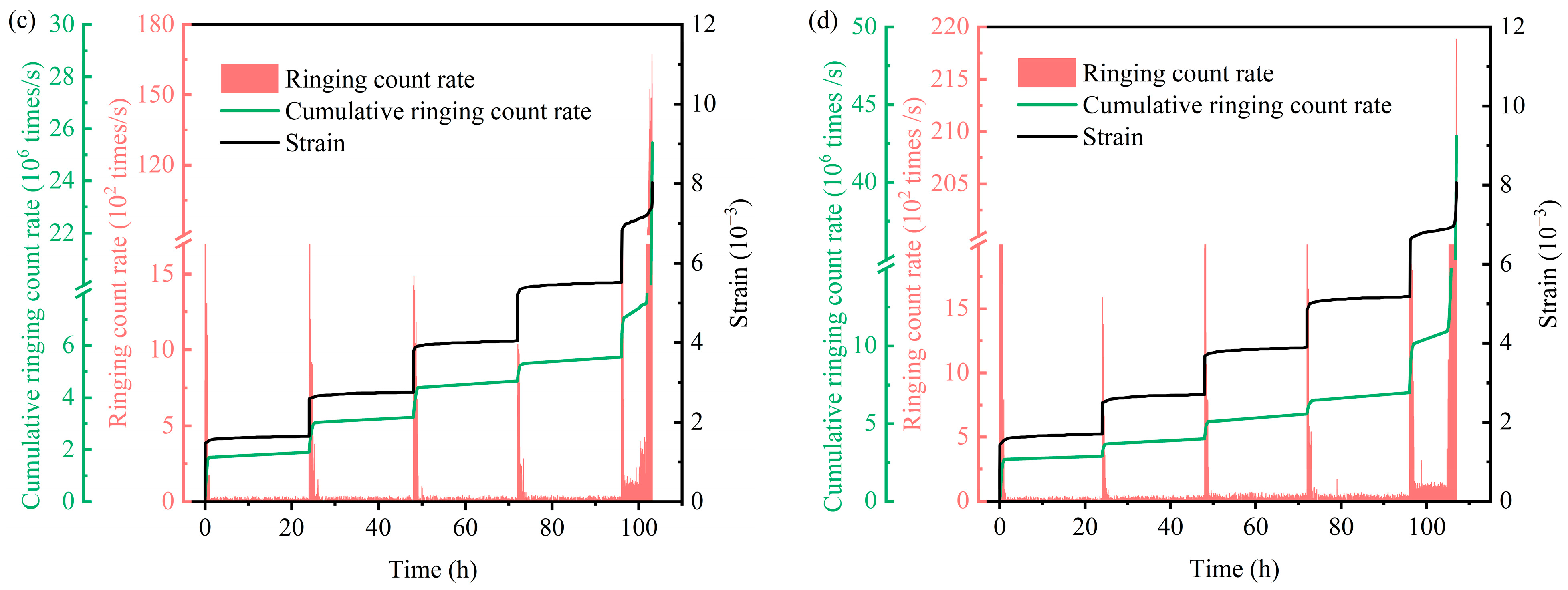
3.2. AE Characteristics
3.2.1. AE Ringing Count Rate
3.2.2. AE B-Value
4. Fractional Nonlinear Creep Damage Model Based on AE Ringing Count Rate
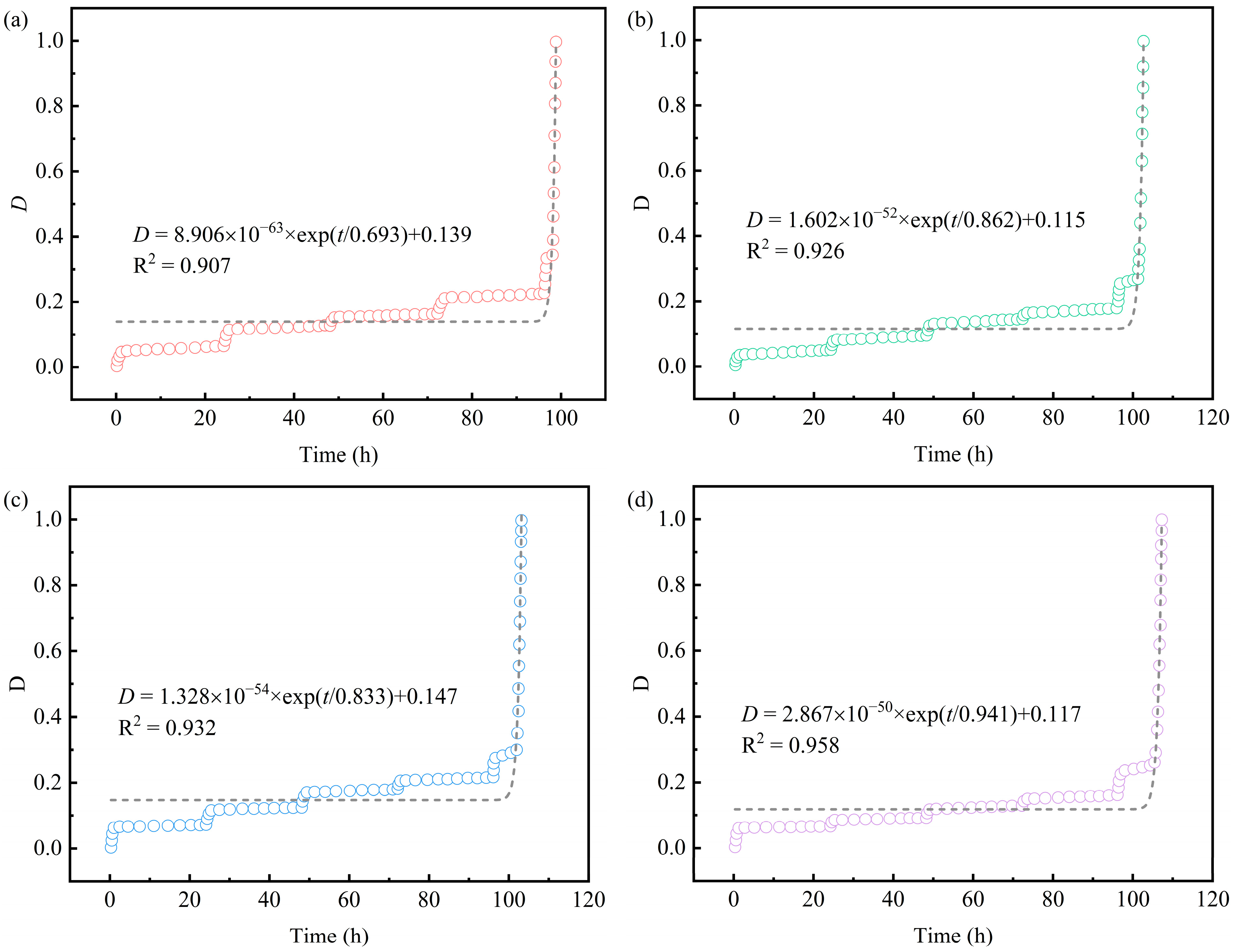
4.1. Damage Quantification Based on AE Ringing Count Rate
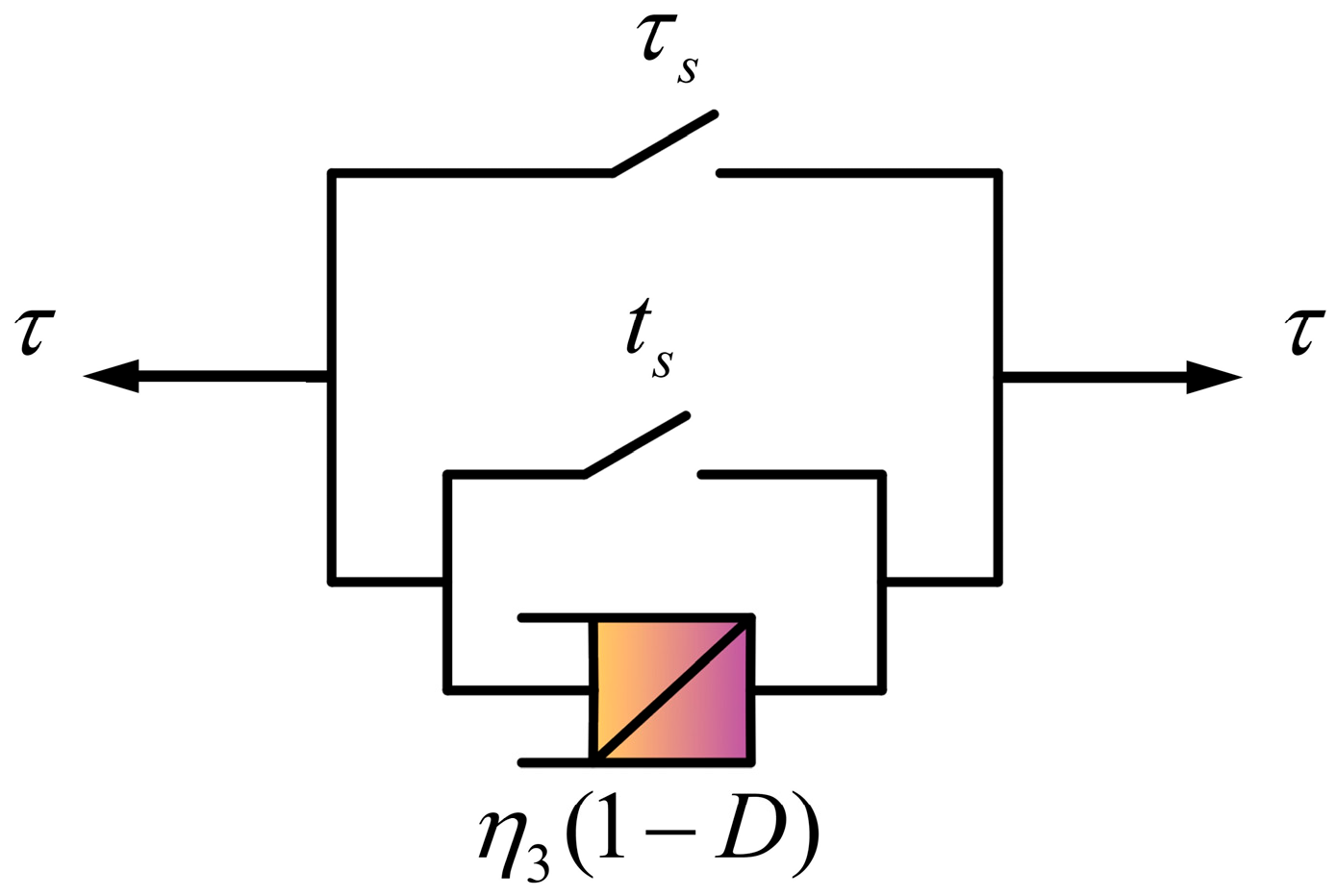
4.2. Fractional Nonlinear Creep Damage Model
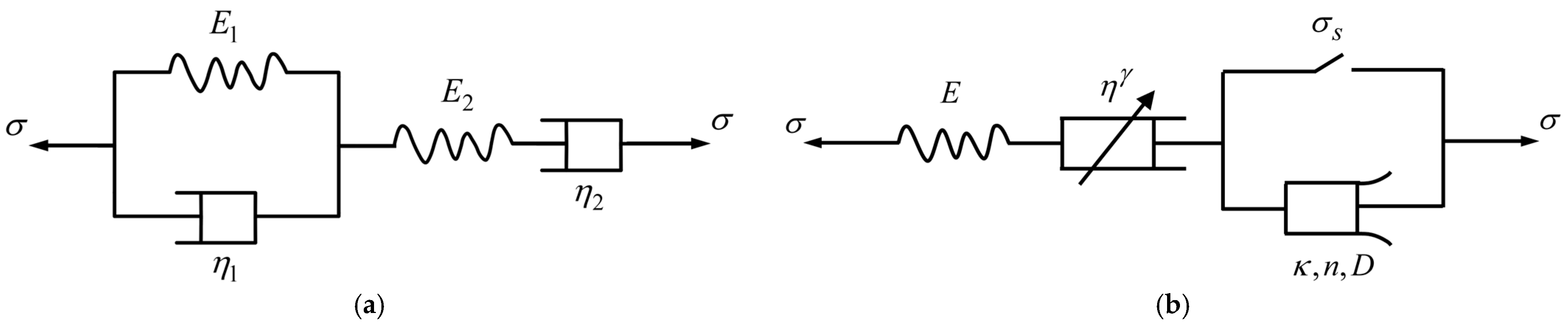
4.2.1. Fractional Derivative and Abel Dashpot
4.2.2. Nonlinear Statistical Damage Body
4.2.3. Creep Equation
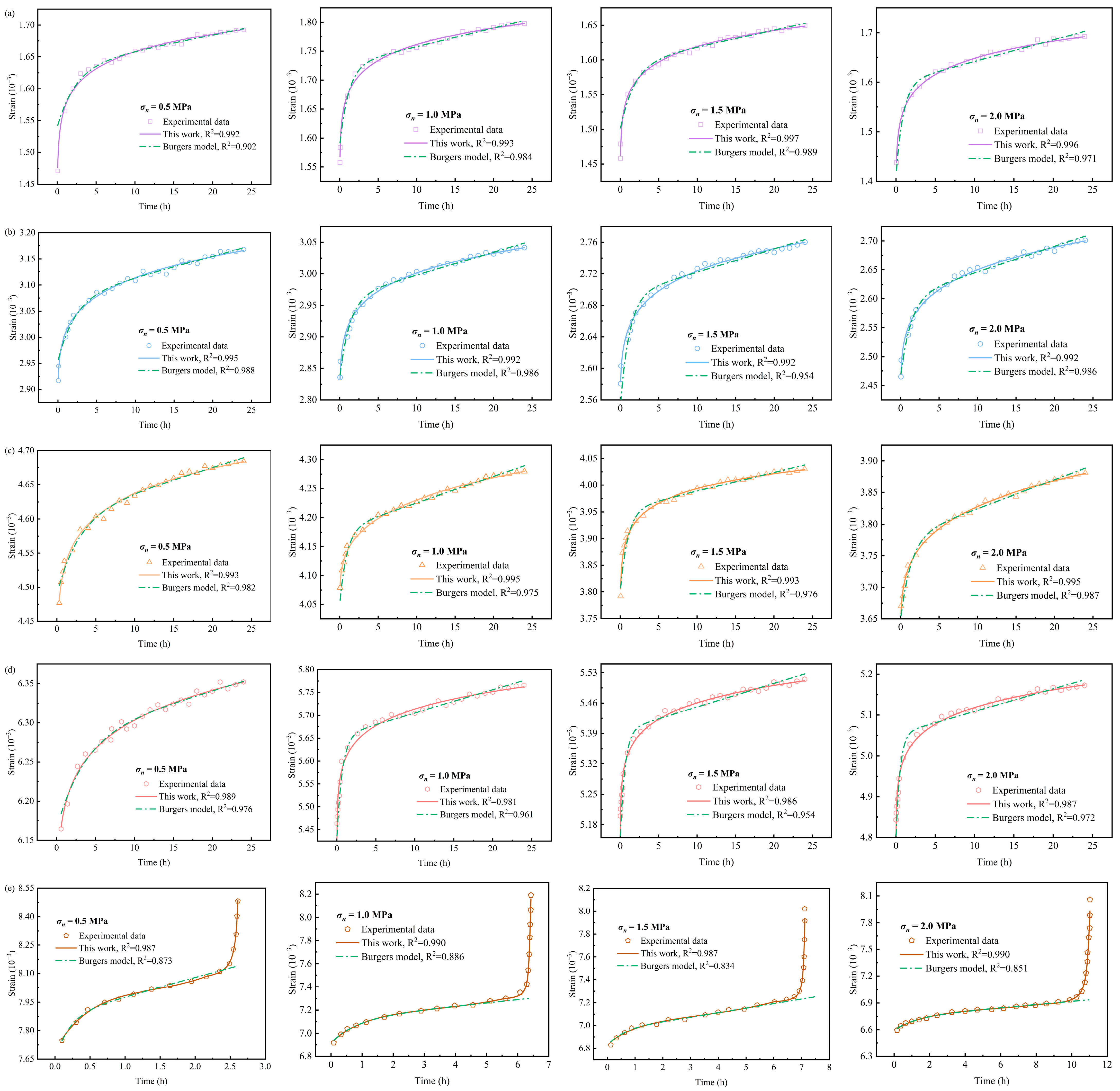
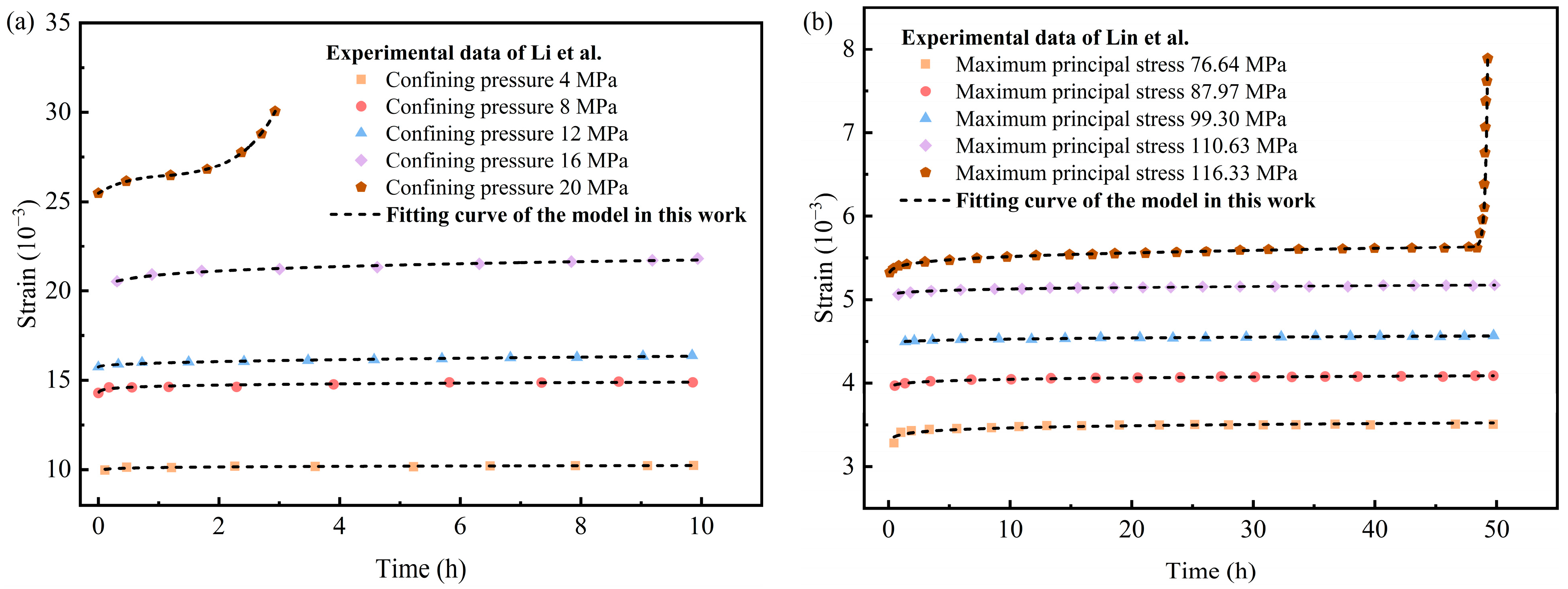
4.3. Model Validation and Discussion
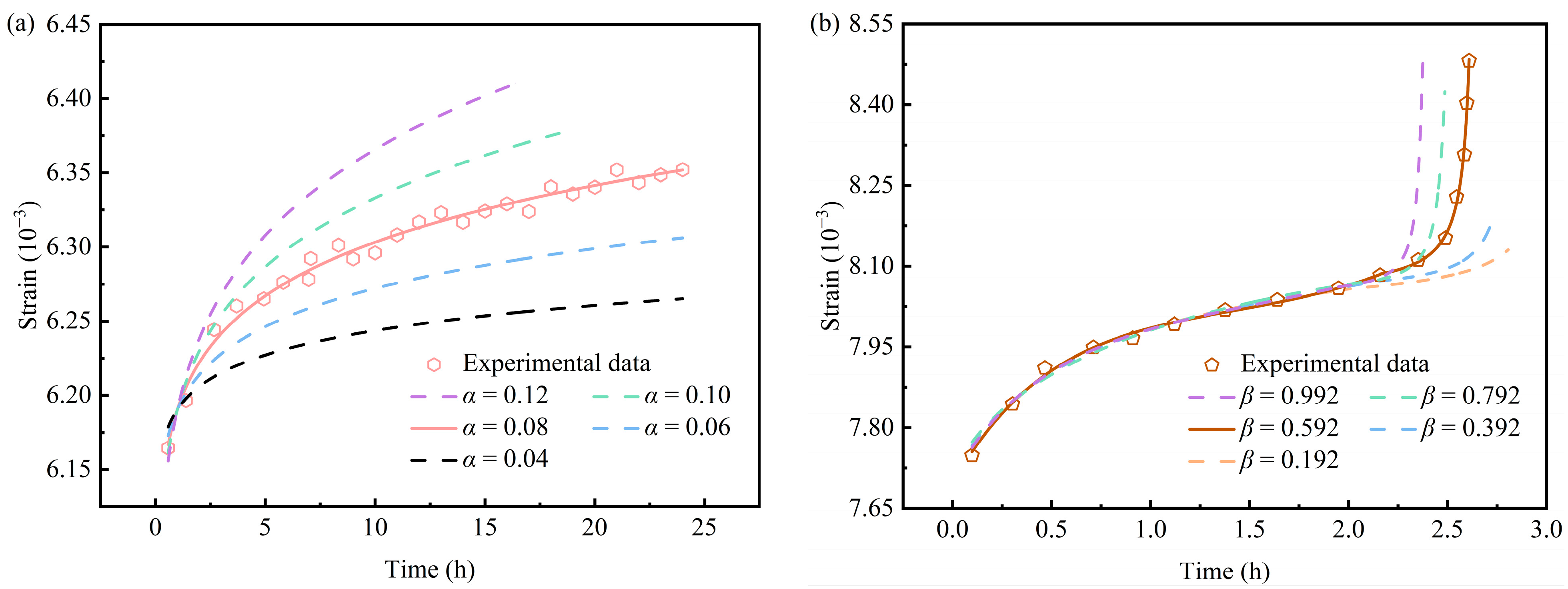
4.4. Sensitivity Analysis of the Parameters
4.5. Superiority of the Creep Model and Its Application
5. Conclusions
- With an increase in normal stress, the shear creep strain of carbonaceous mud shale tended to decay exponentially, while the steady state creep rate increased gradually.
- The peak value and cumulative value of the AE ringing count rate increased gradually with an increase in normal stress. It is also worth noting that there was a corresponding relationship between the step jump of shear strain in carbonaceous mud shale and the peak of the ringing count rate.
- The AE b-value under different normal stresses had a staged pattern of “fluctuation adjustment → stable increase → abrupt decline”. In addition, the sudden drop in the b-value could serve as a precursor feature of creep failure of carbonaceous mud shale, and the higher the normal stress, the earlier the sudden drop in b-value and the larger the Δb-value.
- The damage variable was defined based on the AE ringing count rate, and a nonlinear statistical damage body was proposed. A new creep damage model was constructed by combining fractional-order theory. The model can uniformly describe the creep damage law of carbonaceous mud shale under different normal stresses. The model validation results indicated that the new fractional creep damage model had higher accuracy and applicability, especially in revealing the accelerated creep evolution law of carbonaceous mud shale under failure-level shear stress.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Zheng, D.; Frost, J.D.; Huang, R.Q.; Liu, F.Z. Failure process and modes of rockfall induced by underground mining: A case study of Kaiyang Phosphorite Mine rockfalls. Eng. Geol. 2015, 197, 145–197. [Google Scholar] [CrossRef]
- Tang, H.M.; Zou, Z.X.; Xiong, C.R.; Wu, Y.P.; Hu, X.L.; Wang, L.Q.; Lu, S.; Criss, R.E.; Li, C.D. An evolution model of large consequent bedding rockslides, with particular reference to the Jiweishan rockslide in Southwest China. Eng. Geol. 2015, 186, 17–27. [Google Scholar] [CrossRef]
- Yao, X.; Chen, Y.P.; Liu, D.L.; Zhou, Z.K.; Liesenberg, V.; Junior, J.M.; Li, J. Average-DInSAR method for unstable escarpments detection induced by underground coal mining. Int. J. Appl. Earth Obs. 2021, 103, 102489. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Hu, B.; Li, J.; Huang, L.; Zhang, Z.; Li, B.Y.; Zhong, Z.X.; Wan, C.C. Acid corrosion deterioration of carbonaceous shale: Mechanism revealed from shear properties and macro-micro structure. Constr. Build. Mater. 2025, 474, 141062. [Google Scholar] [CrossRef]
- Duan, S.Q.; Feng, X.T.; Jiang, Q.; Liu, G.F.; Pei, S.F.; Fan, Y.L. In situ observation of failure mechanisms controlled by rock masses with weak interlayer zones in large underground cavern excavations under high geostress. Rock Mech. Rock Eng. 2017, 50, 2465–2493. [Google Scholar] [CrossRef]
- Xu, T.; Xu, Q.; Tang, C.A.; Ranjith, P.G. The evolution of rock failure with discontinuities due to shear creep. Acta Geotech. 2013, 8, 567–581. [Google Scholar] [CrossRef]
- Sun, C.; Jin, C.Z.; Wang, L.G.; Cai, J.Q.; Li, J.D. Creep damage characteristics and slip law of weak-layer mudstone in an open mining slope. Bull. Eng. Geol. Environ. 2023, 82, 399. [Google Scholar] [CrossRef]
- Yang, W.D.; Zhang, Q.Y.; Li, S.C.; Wang, S.G. Estimation of in situ viscoelastic parameters of a weak rock layer by time-dependent plate-loading tests. Int. J. Rock Mech. Min. Sci. 2014, 66, 169–176. [Google Scholar] [CrossRef]
- Ma, C.; Zhan, H.B.; Zhang, T.; Yao, W.M. Investigation on shear behavior of soft interlayers by ring shear tests. Eng. Geol. 2019, 254, 34–42. [Google Scholar] [CrossRef]
- Liang, Z.R.; Chen, Z.X.; Rahman, S.S. Experimental investigation of the primary and secondary creep behaviour of shale gas reservoir rocks from deep sections of the Cooper Basin. J. Nat. Gas Sci. Eng. 2020, 73, 103044. [Google Scholar] [CrossRef]
- Wang, X.K.; Xiang, J.Z.; Xie, W.B.; Xia, C.C.; Yang, J.W.; Wei, W.S. Experimental investigation of the long-term creep behavior of extremely soft coal rocks and novel nonlinear creep mathematical model with a nonstationary viscous coefficient. Bull. Eng. Geol. Environ. 2025, 84, 11–84. [Google Scholar] [CrossRef]
- Ru, W.K.; Hu, S.C.; Zhou, A.H.; Luo, P.K.; Gong, H.; Zhang, C.X.; Zhou, X.D. Study on creep characteristics and nonlinear fractional-order damage constitutive model of weakly cemented soft rock. Rock Mech. Rock Eng. 2023, 56, 8061–8082. [Google Scholar] [CrossRef]
- Sawatsubashi, M.; Kiyota, T.; Katagiri, T. Effect of initial water content and shear stress on immersion-induced creep deformation and strength characteristics of gravelly mudstone. Soils Found. 2021, 61, 1223–1234. [Google Scholar] [CrossRef]
- Zhao, H.B.; Zhang, H.; Li, H.H.; Wang, F.H.; Zhang, M. Formation and fractal characteristics of main fracture surface of red sandstone under restrictive shear creep. Int. J. Rock Mech. Min. Sci. 2017, 98, 181–190. [Google Scholar] [CrossRef]
- Tsai, L.S.; Hsieh, Y.M.; Weng, M.C.; Huang, T.H.; Jeng, F.S. Time-dependent deformation behaviors of weak sandstones. Int. J. Rock Mech. Min. Sci. 2008, 45, 144–154. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, X.L.; Xu, C.; Zhou, C.; He, C.C.; Ying, C.Y. Time-dependent behavior of saturated silty mudstone under different confining pressures. Bull. Eng. Geol. Environ. 2020, 79, 2621–2634. [Google Scholar] [CrossRef]
- Nishii, R.; Matsuoka, N. Monitoring rapid head scarp movement in an alpine rockslide. Eng. Geol. 2010, 115, 49–57. [Google Scholar] [CrossRef]
- Abbas, H.A.; Mohamed, Z.; Kudus, S.A. Deformation behaviour, crack initiation and crack damage of weathered composite sandstone-shale by using the ultrasonic wave and the acoustic emission under uniaxial compressive stress. Int. J. Rock Mech. Min. Sci. 2023, 170, 105497. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Chen, L.G.; Wang, D.; Luan, H.J.; Zhang, G.C.; Dong, L.; Liang, B. Mechanical properties and acoustic emission characteristics of soft rock with different water contents under dynamic disturbance. Int. J. Coal Sci. Technol. 2024, 11, 36. [Google Scholar] [CrossRef]
- Meng, Q.B.; Zhang, M.W.; Han, L.J.; Pu, H.; Chen, Y.L. Acoustic emission characteristics of red sandstone specimens under uniaxial cyclic loading and unloading compression. Rock Mech. Rock Eng. 2018, 51, 969–988. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Zhu, Z.W.; Accornero, F.; Wang, C.L. Multi-technique analysis of seawater impact on the performance of calcium sulphoaluminate cement mortar. Constr. Build. Mater. 2024, 443, 137717. [Google Scholar] [CrossRef]
- Ma, L.J.; Wang, Y.X.; Wang, M.Y.; Xue, B.; Duan, L.Q. Mechanical properties of rock salt under combined creep and fatigue. Int. J. Rock Mech. Min. Sci. 2021, 141, 104654. [Google Scholar] [CrossRef]
- Li, H.R.; Wei, Q.; Xu, Z.; Zhuo, C.Y.; Dong, Z.K.; Zhao, W.G.; Shi, X.L. Empirical analysis of unloading creep damage mechanism of salt rock at 110 °C. Energy 2024, 294, 130908. [Google Scholar] [CrossRef]
- Dong, Z.K.; Li, Y.P.; Li, H.R.; Wang, Z.H.; Shi, X.L.; Chen, X.S.; Lu, Q.F. Experimental study on the influence of temperature on rock salt creep. Rock Mech. Rock Eng. 2023, 56, 3499–3518. [Google Scholar] [CrossRef]
- Zhang, B.H.; Peng, C.B.; Chen, S.H.; Hu, Y.; Li, X.; Zhao, J.Z. The mechanical creep property of shale for different loads and temperatures. Int. J. Rock Mech. Min. Sci. 2023, 163, 105327. [Google Scholar] [CrossRef]
- Li, S.N.; Zhang, J.H.; Chang, J.; Yang, H.; Yue, S.; Peng, J.H.; Chen, K.; Li, Y.; Ren, Z.H.; Chen, W. Quantitative calculation of the damage of carbonaceous mudstone during uniaxial compressive failure process under dry-wet cycling. Bull. Eng. Geol. Environ. 2025, 84, 190. [Google Scholar] [CrossRef]
- Li, J.; Hu, B.; Sheng, J.L.; Zhang, Z. Failure mechanism and treatment of mine landslide with gently-inclined weak interlayer: A case study of Laoyingzui landslide in Emei, Sichuan, China. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 61. [Google Scholar] [CrossRef]
- Feng, X.T.; Haimson, B.; Li, X.C.; Chang, C.D.; Ma, X.D.; Zhang, X.W.; Ingraham, M.; Suzuki, K. ISRM suggested method: Determining deformation and failure characteristics of rocks subjected to true triaxial compression. Rock Mech. Rock Eng. 2019, 52, 2011–2020. [Google Scholar] [CrossRef]
- Ma, T.F.; Liu, H.H.; Zou, Q.L.; Kong, F.J.; Ran, Q.C.; Wang, P.T. Damage evolution characteristics and deterioration mechanism of mechanical properties of sandstone subjected to drying-wetting cycles. J. Mater. Res. Technol. 2023, 23, 4591–4605. [Google Scholar] [CrossRef]
- Aker, E.; Kühn, D.; Vavryčuk, V.; Soldal, M.; Oye, V. Experimental investigation of acoustic emissions and their moment tensors in rock during failure. Int. J. Rock Mech. Min. Sci. 2014, 70, 286–295. [Google Scholar] [CrossRef]
- Ge, Z.L.; Sun, Q. Acoustic emission (AE) characteristics of granite after heating and cooling cycles. Eng. Fract. Mech. 2018, 200, 418–429. [Google Scholar] [CrossRef]
- Goebel, T.H.W.; Schorlemmer, D.; Becker, T.W.; Dresen, G.; Sammis, C.G. Acoustic emissions document stress changes over many seismic cycles in stick-slip experiments. Geophys. Res. Lett. 2013, 40, 2049–2054. [Google Scholar] [CrossRef]
- Iturrioz, I.; Lacidogna, G.; Carpinteri, A. Acoustic emission detection in concrete specimens: Experimental analysis and lattice model simulations. Int. J. Damage Mech. 2014, 23, 327–358. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, C.Y.; Li, B.T.; Zhang, L.H.; Liang, Y.H. Effects of grain dissolution–diffusion sliding and hydro-mechanical interaction on the creep deformation of soft rocks. Acta Geotech. 2020, 15, 1219–1229. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, C.Y.; Li, B.T.; Lu, Y.Q.; Yang, X. A dissolution-diffusion sliding model for soft rock grains with hydro-mechanical effect. J. Rock Mech. Geotech. Eng. 2018, 10, 457–467. [Google Scholar] [CrossRef]
- Zhang, W.M.; Liu, D.W.; Tang, Y.; Qiu, W.C.; Zhang, R.P. Multifractal characteristics of smooth blasting overbreak in extra-long hard rock tunnel. Fractal Fract. 2023, 7, 842. [Google Scholar] [CrossRef]
- Silva, J.; Worsey, T.; Lusk, B. Practical assessment of rock damage due to blasting. Int. J. Min. Sci. Technol. 2019, 29, 379–385. [Google Scholar] [CrossRef]
- Ahmad, M.; Zada, A.; Ghaderi, M.; George, R.; Rezapour, S. On the existence and stability of a neutral stochastic fractional differential system. Fractal Fract. 2022, 6, 203. [Google Scholar] [CrossRef]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fract. 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Zine, H.; Torres, D.F.M. A stochastic fractional calculus with applications to variational principles. Fractal Fract. 2020, 4, 38. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, C.P.; Han, B.B.; Duan, Z.Q. A creep constitutive model for salt rock based on fractional derivatives. Int. J. Rock Mech. Min. Sci. 2011, 48, 116–121. [Google Scholar] [CrossRef]
- Jiang, X.X.; Wang, J.W.; Wang, W.; Zhang, H.X. A predictor-corrector compact difference scheme for a nonlinear fractional differential equation. Fractal Fract. 2023, 7, 521. [Google Scholar] [CrossRef]
- Lupulescu, V. Fractional calculus for interval-valued functions. Fuzzy Set. Syst. 2015, 265, 63–85. [Google Scholar] [CrossRef]
- Li, J.; Hu, B.; Sheng, J.L.; Huang, L. A fractional-order creep-damage model for carbonaceous shale describing coupled damage caused by rainfall and blasting. Fractal Fract. 2024, 8, 459. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, C.P.; Mishnaevsky, L.; Duan, Z.Q.; Ding, J.Y. A fractional derivative approach to full creep regions in salt rock. Mech. Time-Depend. Mater. 2013, 17, 413–425. [Google Scholar] [CrossRef]
- Wu, J.; Wang, W.; Cao, Y.J.; Liu, S.F.; Zhang, Q.; Chu, W.J. A novel nonlinear fractional viscoelastic-viscoplastic damage creep model for rock-like geomaterials. Comput. Geotech. 2023, 163, 105726. [Google Scholar] [CrossRef]
- Zhou, H.W.; Jin, Z.M. Fractional derivative triaxial creep model of Beishan granite considering probabilistic damage evolution. Acta Geotech. 2023, 18, 4017–4033. [Google Scholar] [CrossRef]
- Li, J.D.; Gao, Y.; Yang, T.H.; Zhang, P.H.; Deng, W.X.; Liu, F.Y. Effect of water on the rock strength and creep behavior of green mudstone. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 101. [Google Scholar] [CrossRef]
- Lin, H.X.; Zhang, Q.Y.; Zhang, L.Y.; Duan, K.; Xue, T.E.; Fan, Q.H. The influence of water content on the time-dependent mechanical behavior of argillaceous siltstone. Rock Mech. Rock Eng. 2022, 55, 3939–3957. [Google Scholar] [CrossRef]


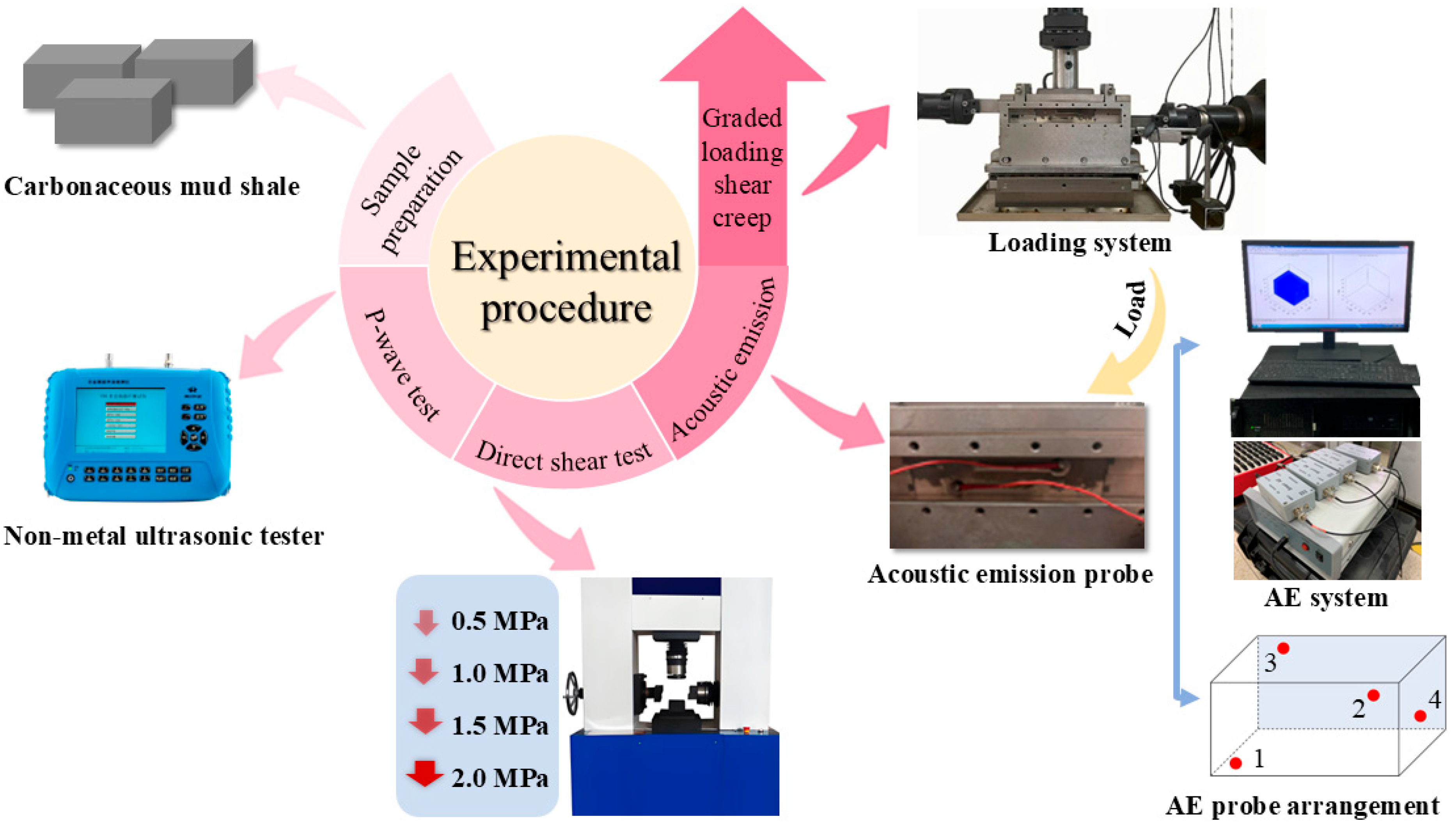




| AE Probe Coordinates (mm) | Probe Arrangement | |||
|---|---|---|---|---|
| N | x | y | z | |
| 1 | 75 | 20 | 10 |  |
| 2 | 75 | 130 | 65 | |
| 3 | 0 | 20 | 65 | |
| 4 | 0 | 130 | 10 | |
| /MPa | /MPa | Shear Stress /MPa | ||||
|---|---|---|---|---|---|---|
| 0.5 | 2.24 | 0.89 | 1.12 | 1.35 | 1.56 | 1.79 |
| 1.0 | 2.66 | 1.06 | 1.33 | 1.59 | 1.85 | 2.12 |
| 1.5 | 2.99 | 1.19 | 1.49 | 1.79 | 2.08 | 2.38 |
| 2.0 | 3.47 | 1.39 | 1.73 | 2.08 | 2.42 | 2.77 |
| /MPa | /MPa | /GPa | /GPa·h | /GPa·h | /GPa·h | |||
|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.89 | 1.376 | 0.982 | 0.039 | 0.992 | |||
| 1.12 | 0.401 | 2.296 | 0.174 | 0.995 | ||||
| 1.35 | 0.338 | 1.596 | 0.081 | 0.993 | ||||
| 1.56 | 0.277 | 1.683 | 0.075 | 0.989 | ||||
| 1.79 | 0.233 | 0.255 | 0.169 | 0.249 | 0.592 | 15.827 | 0.987 | |
| 1.0 | 1.06 | 1.003 | 1.311 | 0.058 | 0.993 | |||
| 1.33 | 0.499 | 2.311 | 0.129 | 0.992 | ||||
| 1.59 | 0.394 | 3.839 | 0.258 | 0.995 | ||||
| 1.85 | 0.365 | 1.856 | 0.083 | 0.981 | ||||
| 2.12 | 0.306 | 0.856 | 0.155 | 0.446 | 0.607 | 34.532 | 0.990 | |
| 1.5 | 1.19 | 1.128 | 1.553 | 0.058 | 0.997 | |||
| 1.49 | 0.602 | 2.929 | 0.156 | 0.992 | ||||
| 1.79 | 0.581 | 1.472 | 0.044 | 0.993 | ||||
| 2.08 | 0.438 | 1.874 | 0.079 | 0.986 | ||||
| 2.38 | 0.349 | 0.797 | 0.407 | 0.383 | 0.533 | 13.189 | 0.987 | |
| 2.0 | 1.39 | 1.495 | 1.504 | 0.068 | 0.996 | |||
| 1.73 | 0.733 | 3.011 | 0.182 | 0.992 | ||||
| 2.08 | 0.581 | 3.729 | 0.291 | 0.995 | ||||
| 2.42 | 0.545 | 2.094 | 0.090 | 0.987 | ||||
| 2.77 | 0.420 | 1.089 | 0.144 | 0.389 | 0.371 | 35.734 | 0.990 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Hu, B.; Li, J.; Zhang, X.; Dai, X.; Cui, K. Fractional-Order Constitutive Modeling of Shear Creep Damage in Carbonaceous Mud Shale: Experimental Verification of Acoustic Emission Ringing Count Rate Analysis. Fractal Fract. 2025, 9, 610. https://doi.org/10.3390/fractalfract9090610
Wu J, Hu B, Li J, Zhang X, Dai X, Cui K. Fractional-Order Constitutive Modeling of Shear Creep Damage in Carbonaceous Mud Shale: Experimental Verification of Acoustic Emission Ringing Count Rate Analysis. Fractal and Fractional. 2025; 9(9):610. https://doi.org/10.3390/fractalfract9090610
Chicago/Turabian StyleWu, Jinpeng, Bin Hu, Jing Li, Xiangyu Zhang, Xin Dai, and Kai Cui. 2025. "Fractional-Order Constitutive Modeling of Shear Creep Damage in Carbonaceous Mud Shale: Experimental Verification of Acoustic Emission Ringing Count Rate Analysis" Fractal and Fractional 9, no. 9: 610. https://doi.org/10.3390/fractalfract9090610
APA StyleWu, J., Hu, B., Li, J., Zhang, X., Dai, X., & Cui, K. (2025). Fractional-Order Constitutive Modeling of Shear Creep Damage in Carbonaceous Mud Shale: Experimental Verification of Acoustic Emission Ringing Count Rate Analysis. Fractal and Fractional, 9(9), 610. https://doi.org/10.3390/fractalfract9090610






