Arithmetic Harris Hawks-Based Effective Battery Charging from Variable Sources and Energy Recovery Through Regenerative Braking in Electric Vehicles, Implying Fractional Order PID Controller
Abstract
1. Introduction
2. Methodology
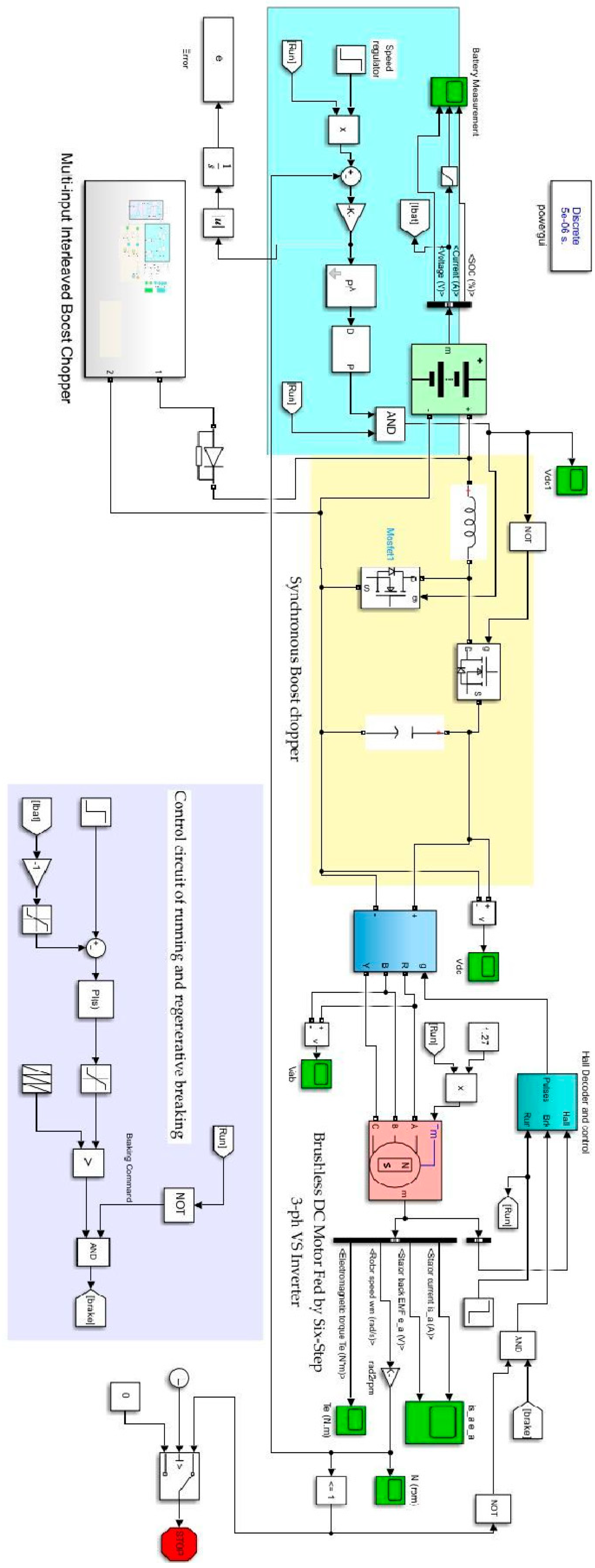
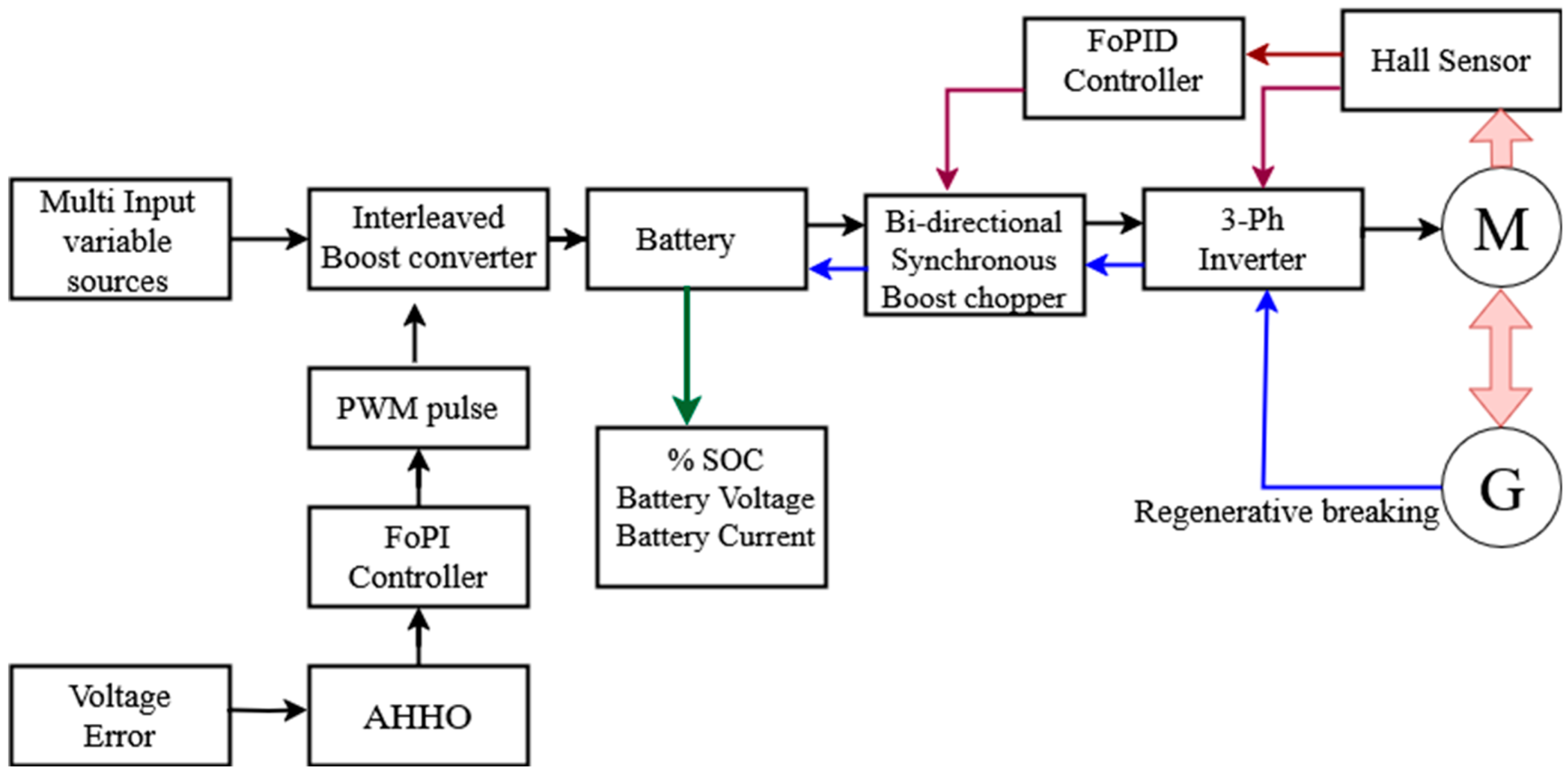
2.1. Architecture of Proposed Scheme of Battery Charging and Regenerative Braking Applied in EV
- High Efficiency: BLDC motors exhibit exceptional efficiency across various operational conditions, ensuring optimal energy utilization and minimizing losses.
- Power Density: The design of BLDC motors enables compact structures and lightweight construction, leading to an enhanced power-to-weight ratio.
- Prolonged Lifespan: The absence of brushes in BLDC motors reduces mechanical wear, leading to extended operational lifespans and fewer maintenance requirements.
- Regenerative Braking: BLDC motors facilitate regenerative braking, converting kinetic energy into electrical energy during deceleration, hence enhancing energy recovery.
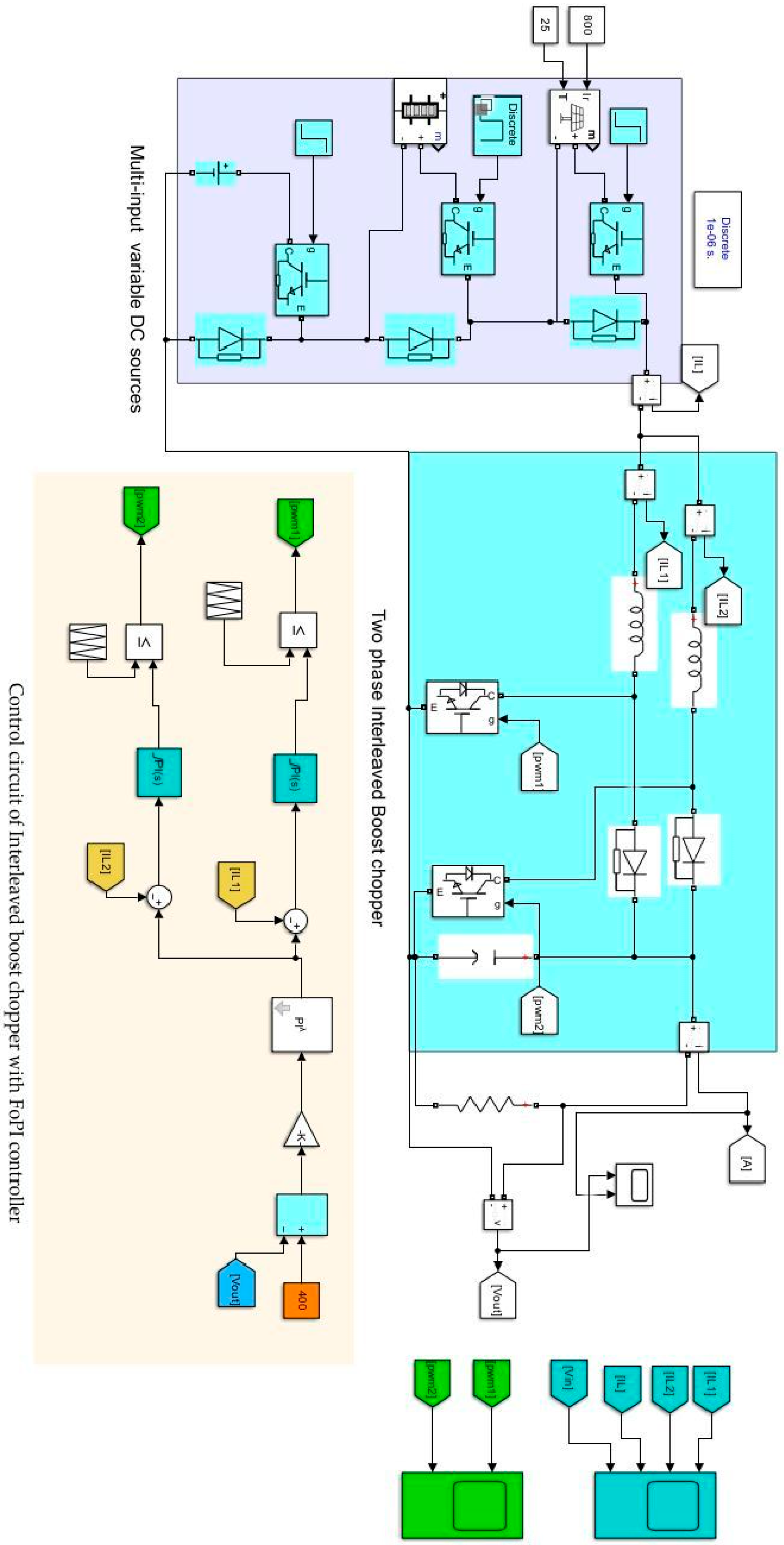
2.2. Multi-Input Interleaved Boost Chopper for Fast and Effective Charging of Battery Source of EVs
2.3. Chopper-Controlled BLDC Applied in EV
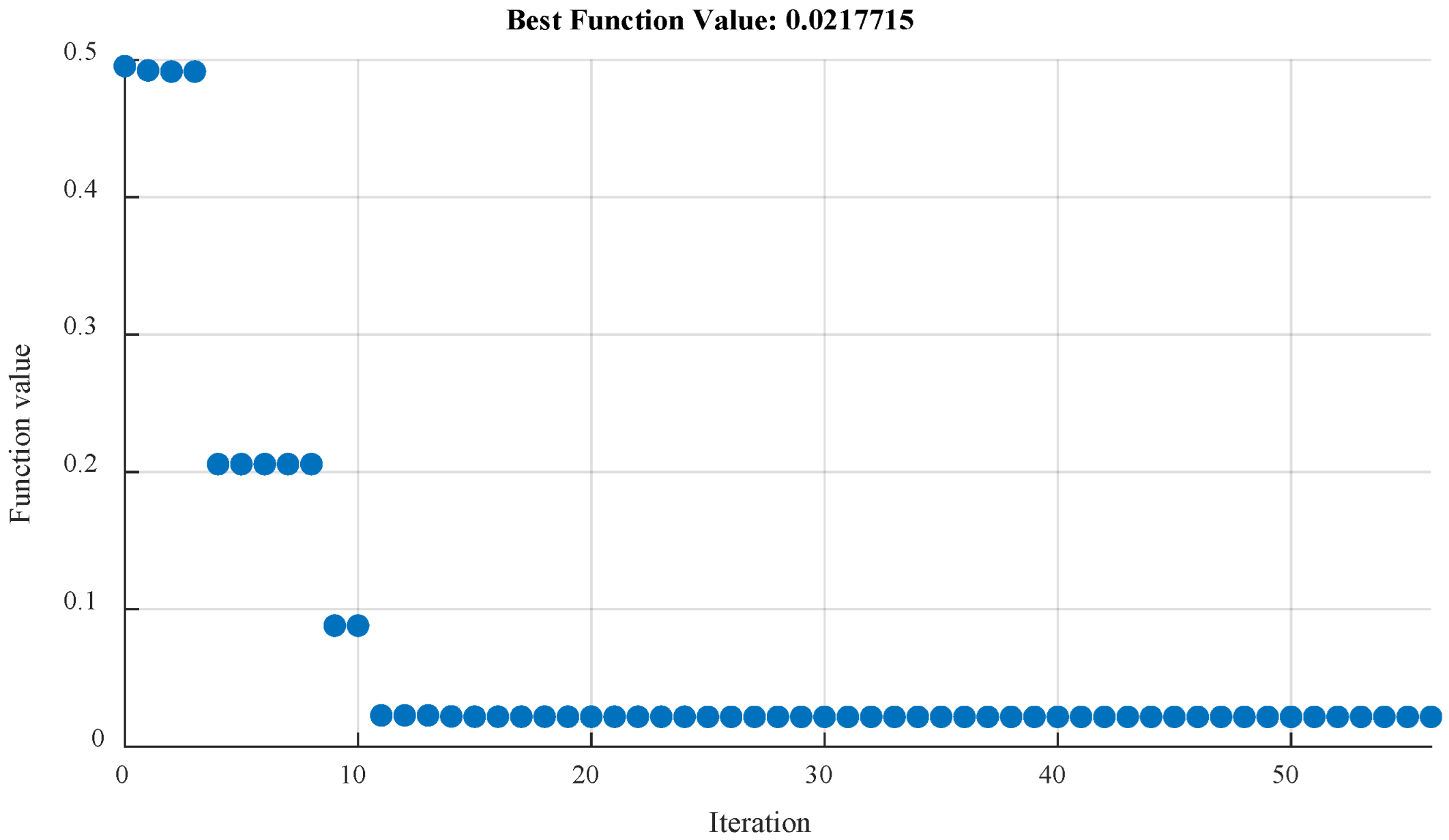
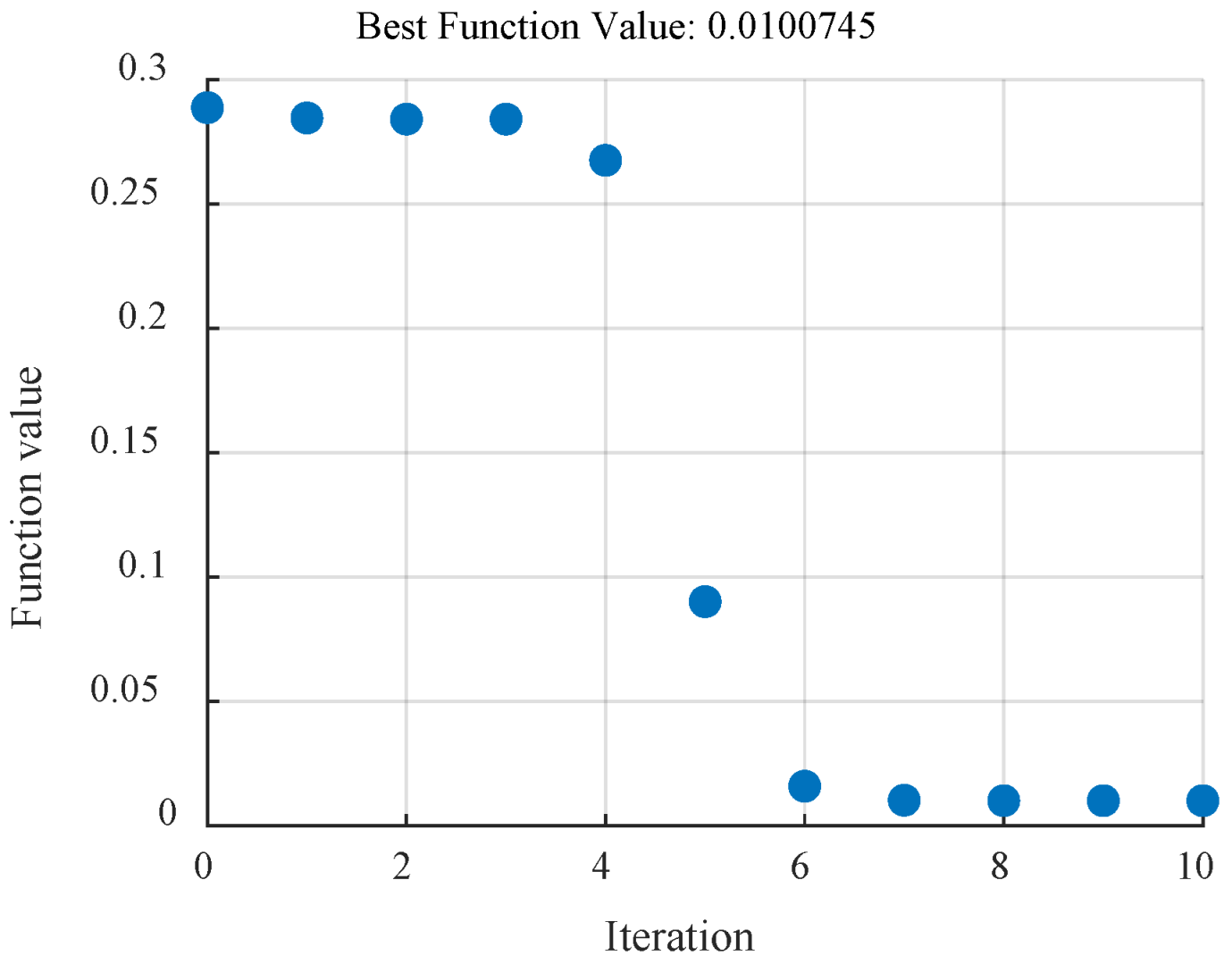
3. Arithmetic Harris Hawks Optimization for Tuning of PI and FoPI
3.1. Error Criteria Expressions
- Integral Absolute Error (IAE):
- Integral of Squared Error (ISE):
- Integral Time-Weighted Absolute Error (ITAE):
- Integral Time-Weighted Squared Error (ITSE):
- System Model: The mathematical model of the system (e.g., transfer function).
- Controller Type:
- PI Controller: Kp (proportional gain) and Ki (integral gain).
- FoPI Controller: , , and (fractional integral order).
- AHHO Parameters:
- Population size .
- Maximum number of iterations .
- Bounds for each parameter , , and .
- Optimized parameters , , and (for FoPI).
- Minimum value of the chosen error criterion.
3.2. Algorithm Steps
- Initialize Parameters:
- Define population size , maximum iteration , and parameter bounds for , , and .
- Randomly initialize each hawk’s position within the parameter bounds:
- For the PI controller, each hawk is defined as
- For the FOPI controller, each hawk is defined as
- 2.
- Evaluate Initial Fitness:
- For each hawk, simulate the system response with its controller parameters.
- Calculate the chosen error criterion (e.g., IAE, ITAE) for each hawk.
- Identify and store the best hawk with the minimum error criterion value.
- 3.
- Iterative Optimization (for each iteration ):
- Update Escape Energy E:
- Calculate the escape energy as follows:where denotes the initial energy state of the prey, which is randomly within the interval at each iteration.
- The value of decreases from to as iterations progress, driving the transition from exploration to exploitation.
- Exploration Phase ():
- When , hawks explore the search space.
- For each hawk , update its position based on the following:
- Here, is the best hawk’s position, is a randomly selected hawk, and is a random value in .
- Exploitation Phase ():
- When , hawks shift to targeting the best hawk closely.
- Soft Besiege ():
- For moderate escape energy, hawks approach the best hawk cautiously:where is a random value in to allow adaptive movement.
- Hard Besiege (if ):
- For very low escape energy, hawks move directly toward the best hawk:where is a small random value allowing local exploitation.
- Boundary Check:
- Ensure that the hawk’s updated position stays within the specified bounds.
- Evaluate Fitness:
- Calculate the fitness (error criterion) for each hawk’s new position.
- Update the best hawk if a better fitness value is found.
- 4.
- Termination Check:
- If the maximum number of iterations is reached or if the improvement in fitness is below a threshold, end the algorithm.
- 5.
- Return Optimal Parameters:
- Output the optimal values of , , and (if FOPI), along with the minimized error criteria.
3.3. Computational Complexity
3.3.1. Notation and Parameters
- : Population size (number of hawks).
- : Maximum number of iterations.
- : Dimensionality of the problem (number of parameters to optimize).
- For PI controllers, (parameters and ).
- For FoPI controllers, (parameters , , and ).
- : Time complexity of a single fitness evaluation, which includes the following:
- Simulating the system with current controller parameters.
- Computing the performance criterion (e.g., IAE, ITAE).
3.3.2. Complexity Breakdown of the AHHO Algorithm
- Random Initialization of Hawk Positions:
- Each hawk is initialized with random values within defined bounds for parameters.
- This requires operations to set up the initial population.
- 2.
- Initial Fitness Evaluation:
- The fitness of each hawk is evaluated initially by simulating the system and calculating the error criterion.
- Given hawks, the complexity of initial fitness evaluations is .
- Escape Energy Update:
- Escape energy is calculated once per iteration and is constant in time, .
- 2.
- Exploration and Exploitation Phases:
- Each hawk’s position is updated based on the value of :
- Exploration Phase ():
- The hawk position’s update formula involves simple arithmetic operations, which have a time complexity of for each hawk.
- Exploitation Phase ():
- Position updates also require operations per hawk, regardless of the specific exploitation mode (soft or hard besiege).
- Complexity of Position Updates for All Hawks:
- 3.
- Boundary Check:
- Each hawk’s position is checked against boundary constraints after each update, which has a time complexity of per hawk.
- For all hawks, this requires operations.
- 4.
- Fitness Evaluation:
- Each hawk’s fitness is recalculated based on its updated parameters.
- The complexity of evaluating fitness for all hawks in each iteration is .
- 5.
- Best Hawk Update:
- At the end of each iteration, the hawk with the best fitness is updated.
- This involves scanning the fitness values of all hawks, which has a complexity of .
3.3.3. Overall Complexity of the AHHO Algorithm
3.3.4. Computational Complexity for PI and FoPI Controllers
- PI Controller ():
- FoPI Controller ():
3.3.5. Dominant Term: Fitness Evaluation Complexity
- : Number of hawks (population size);
- : Number of parameters (two for PI and three for FoPI);
- : Complexity of fitness evaluation (dominated by system simulation);
- : Maximum number of iterations.
4. Results and Discussions
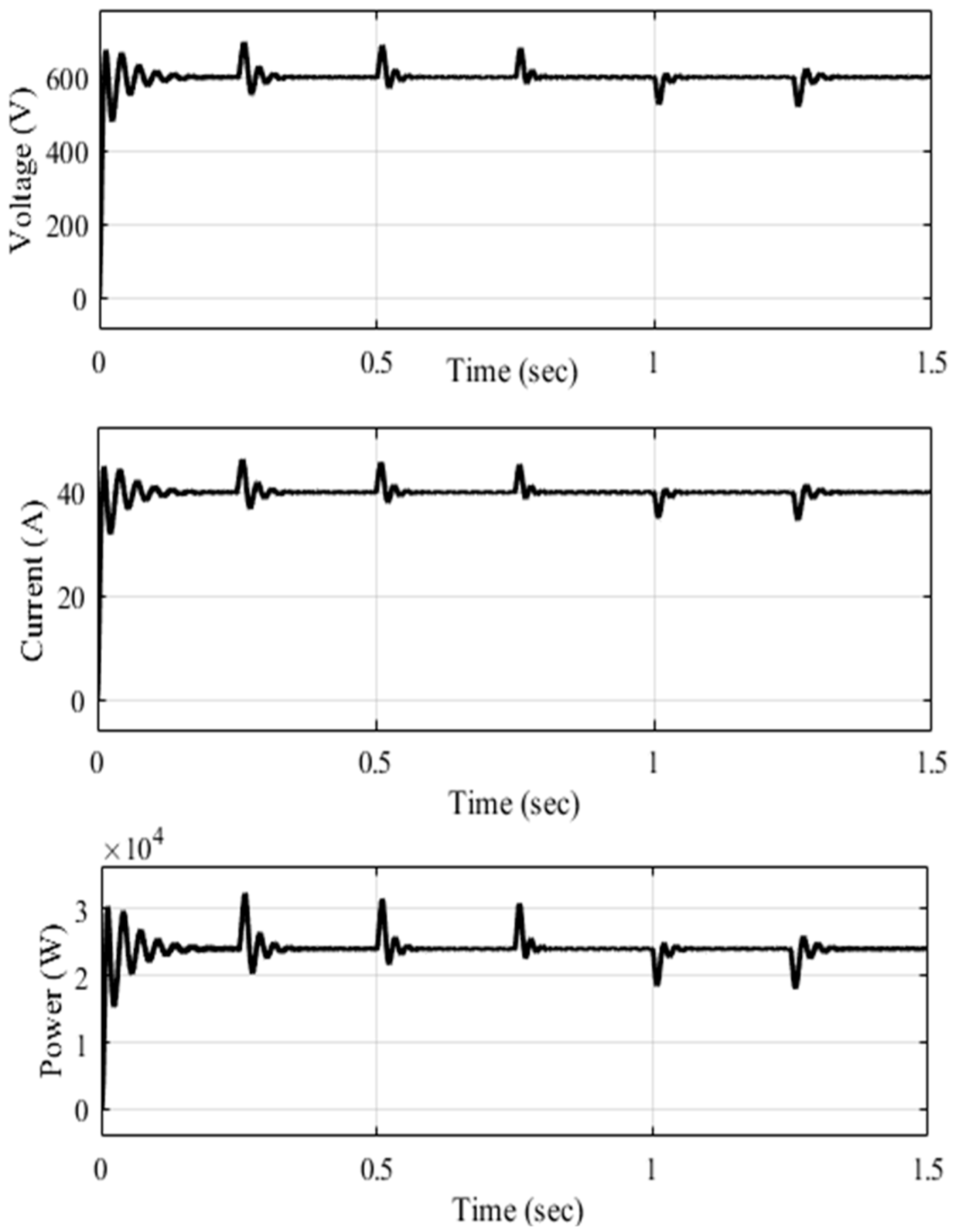
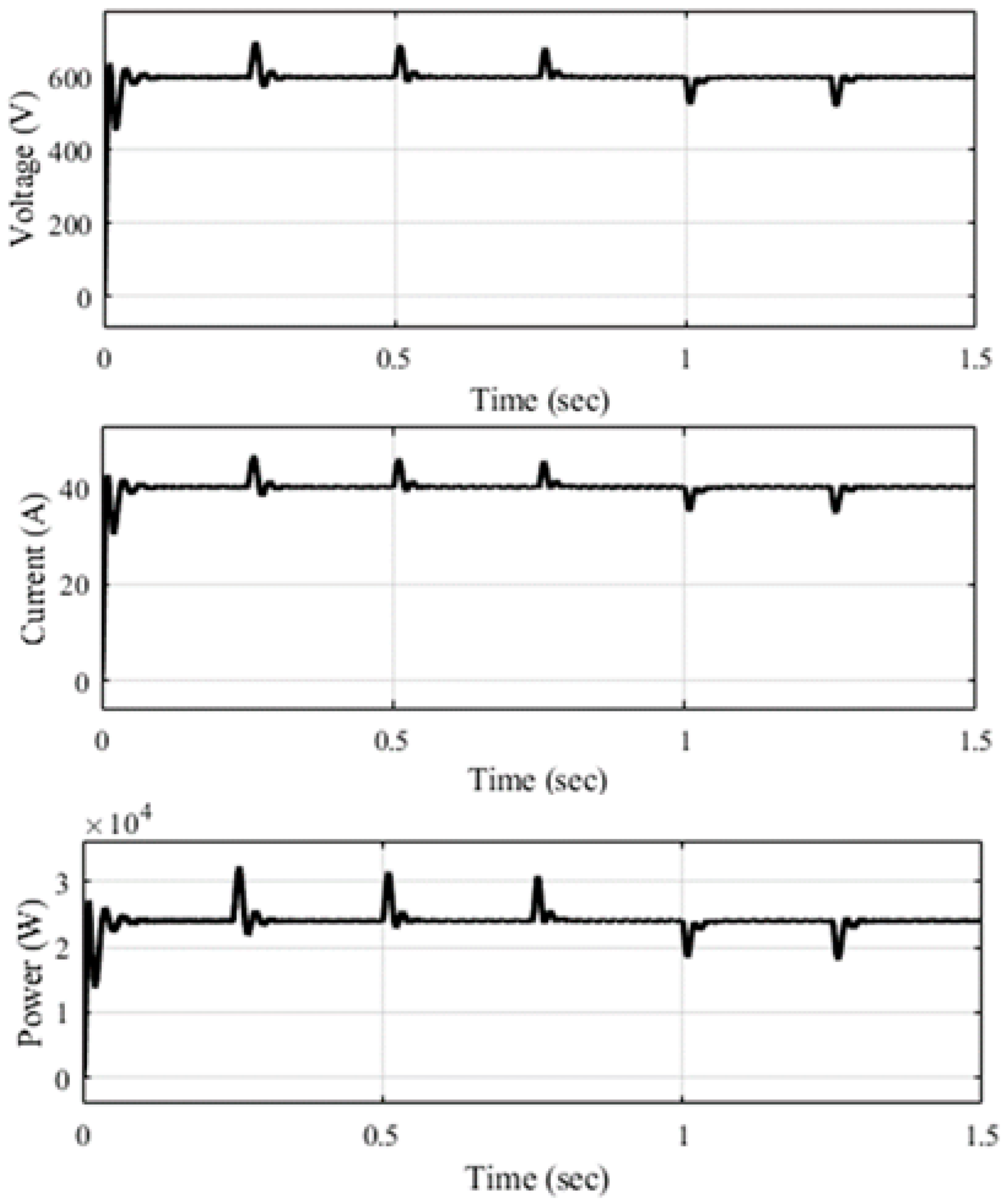
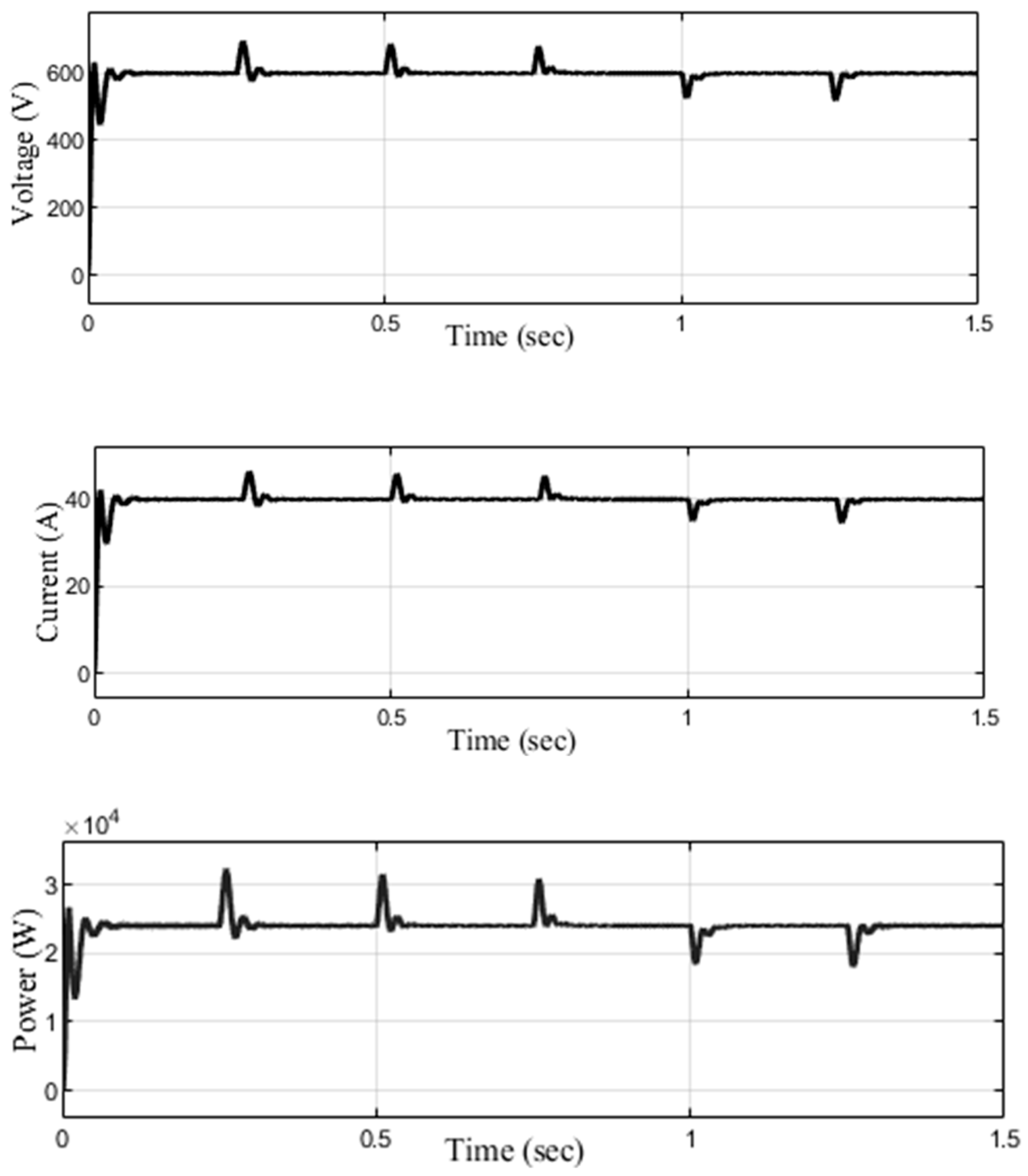
4.1. Interleaved Boost Chopper for Effective Battery Charging Using Tuned PI and FoPI Controllers
4.1.1. Using PI Controllers Tuned with Ziegler–Nichols (Z-N) Method
4.1.2. Using PI Controllers Tuned with AHHO Algorithm
4.1.3. Using FoPI Controllers Tuned with AHHO Algorithm
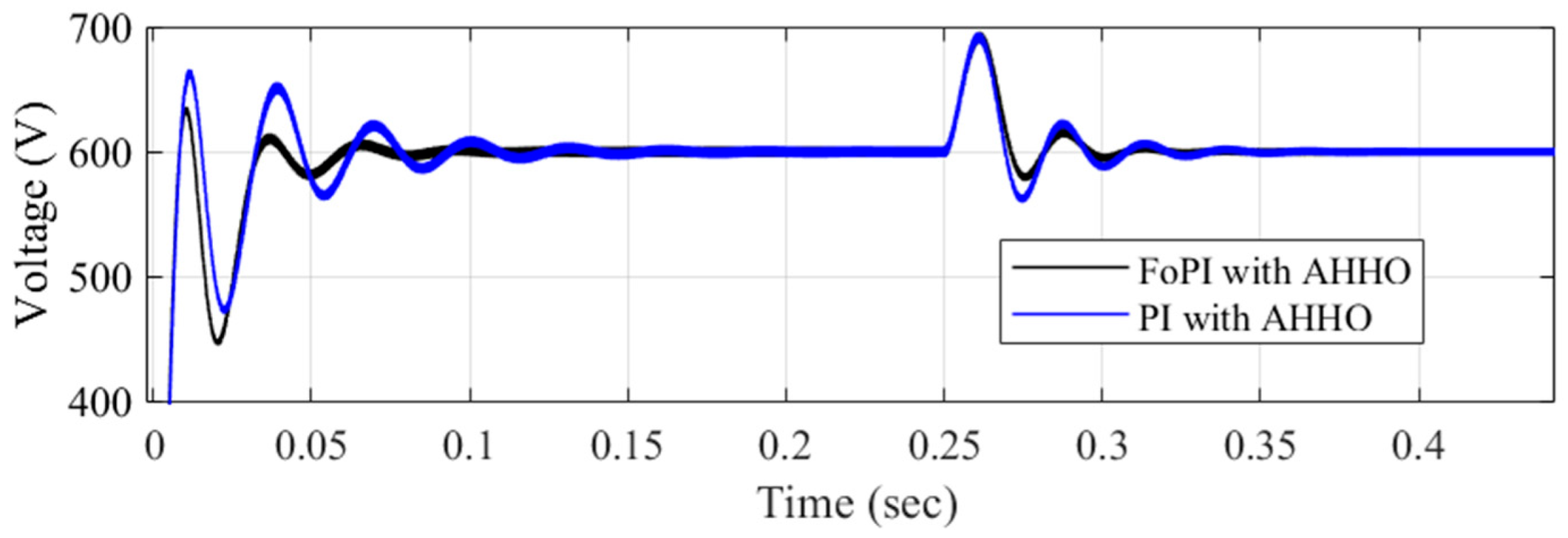
4.1.4. Transient Analysis of the System
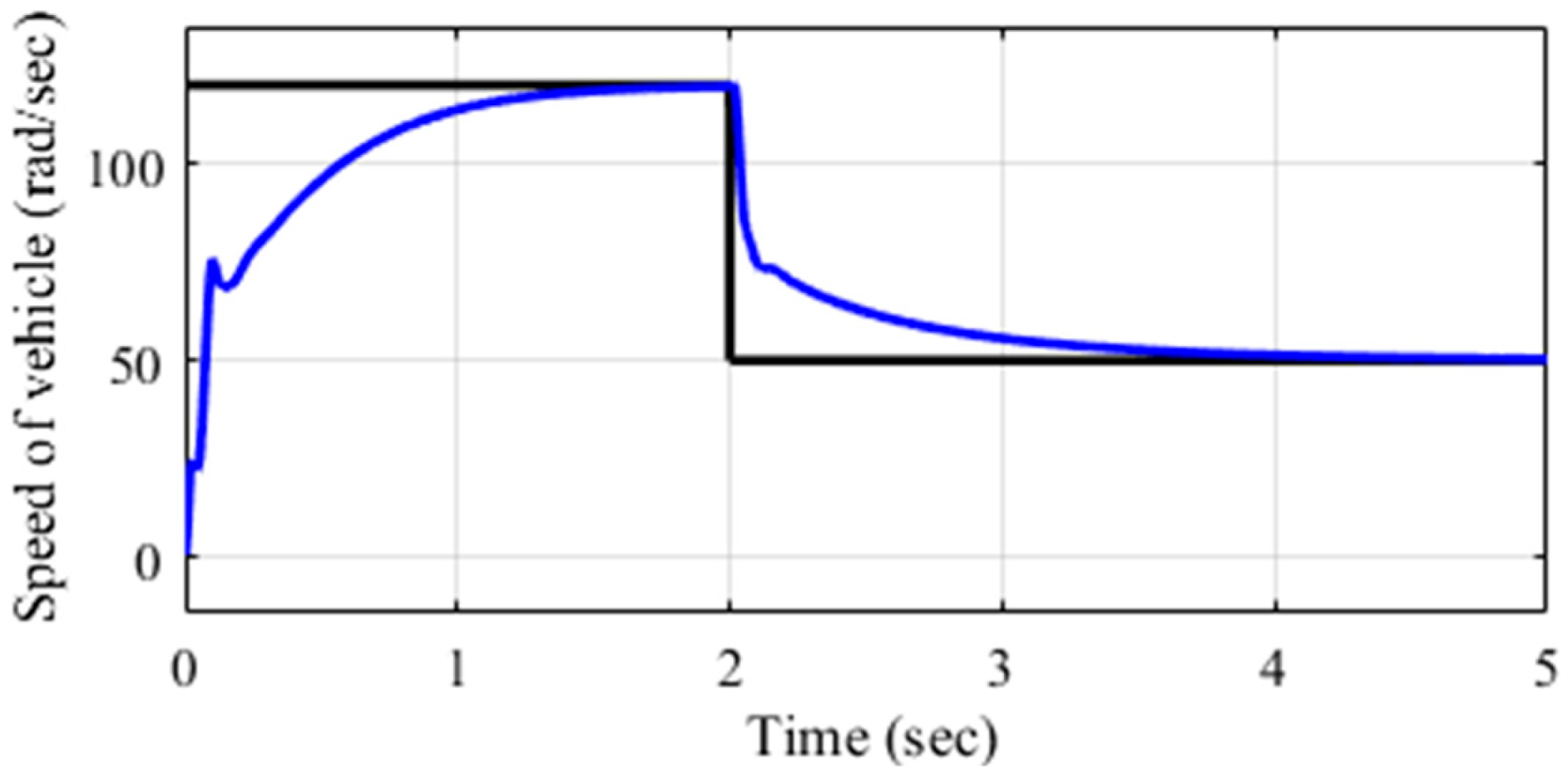
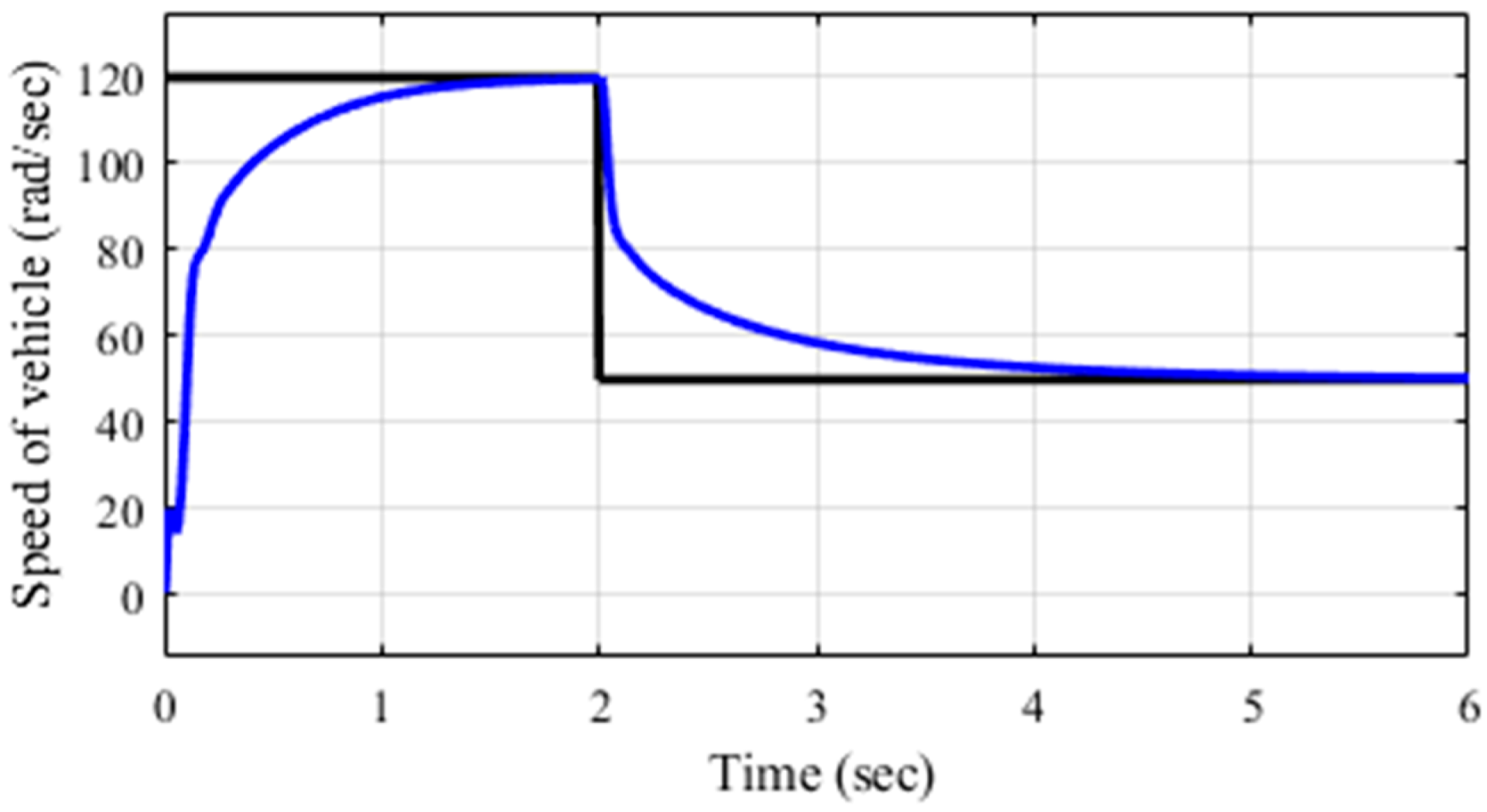
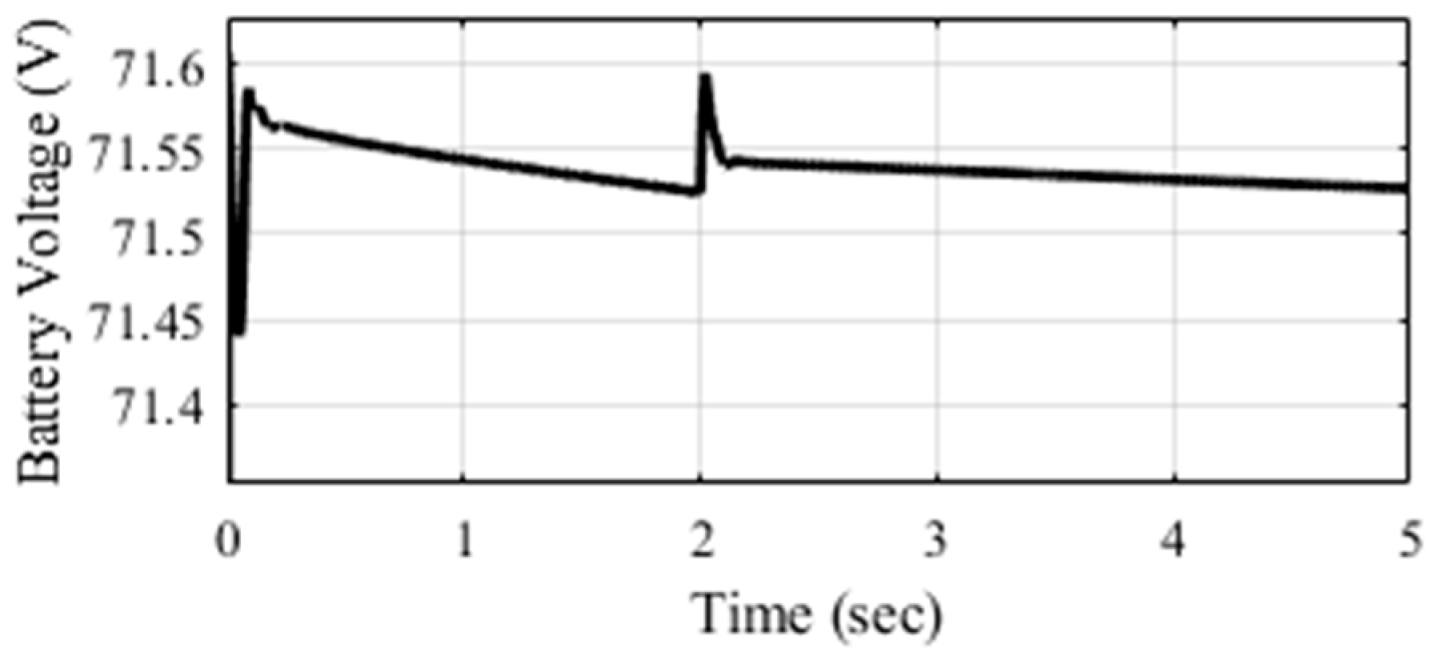
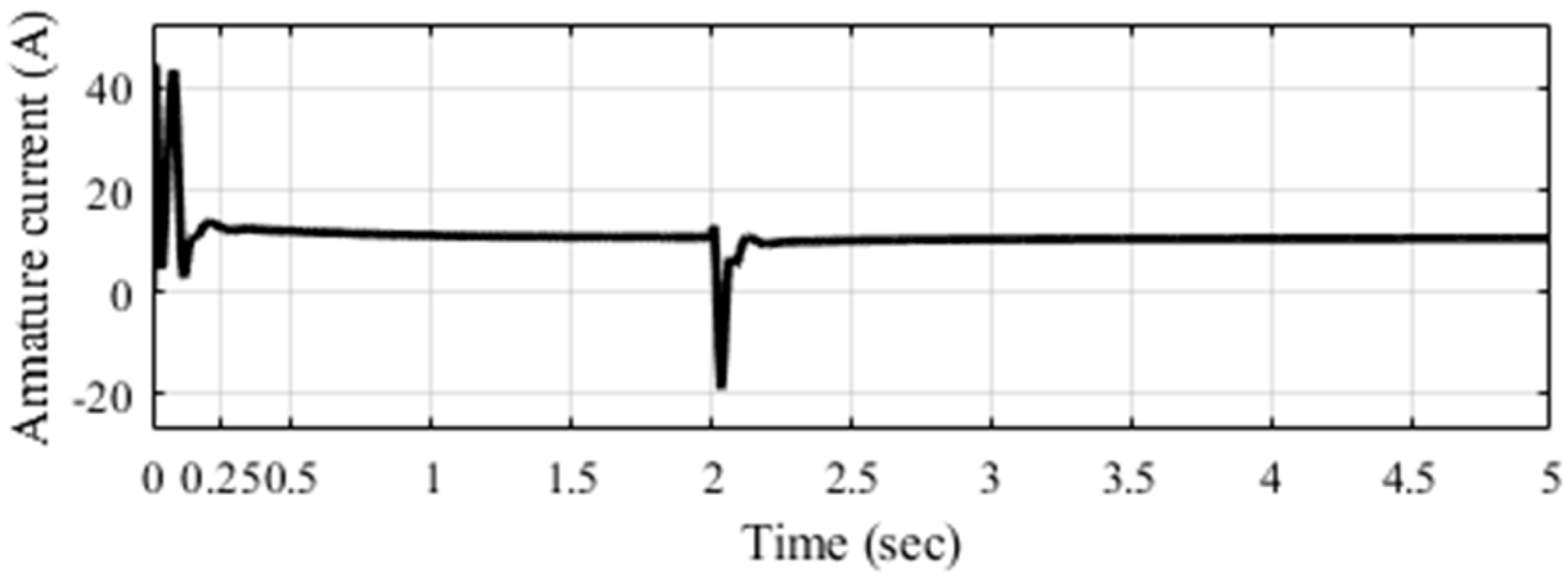
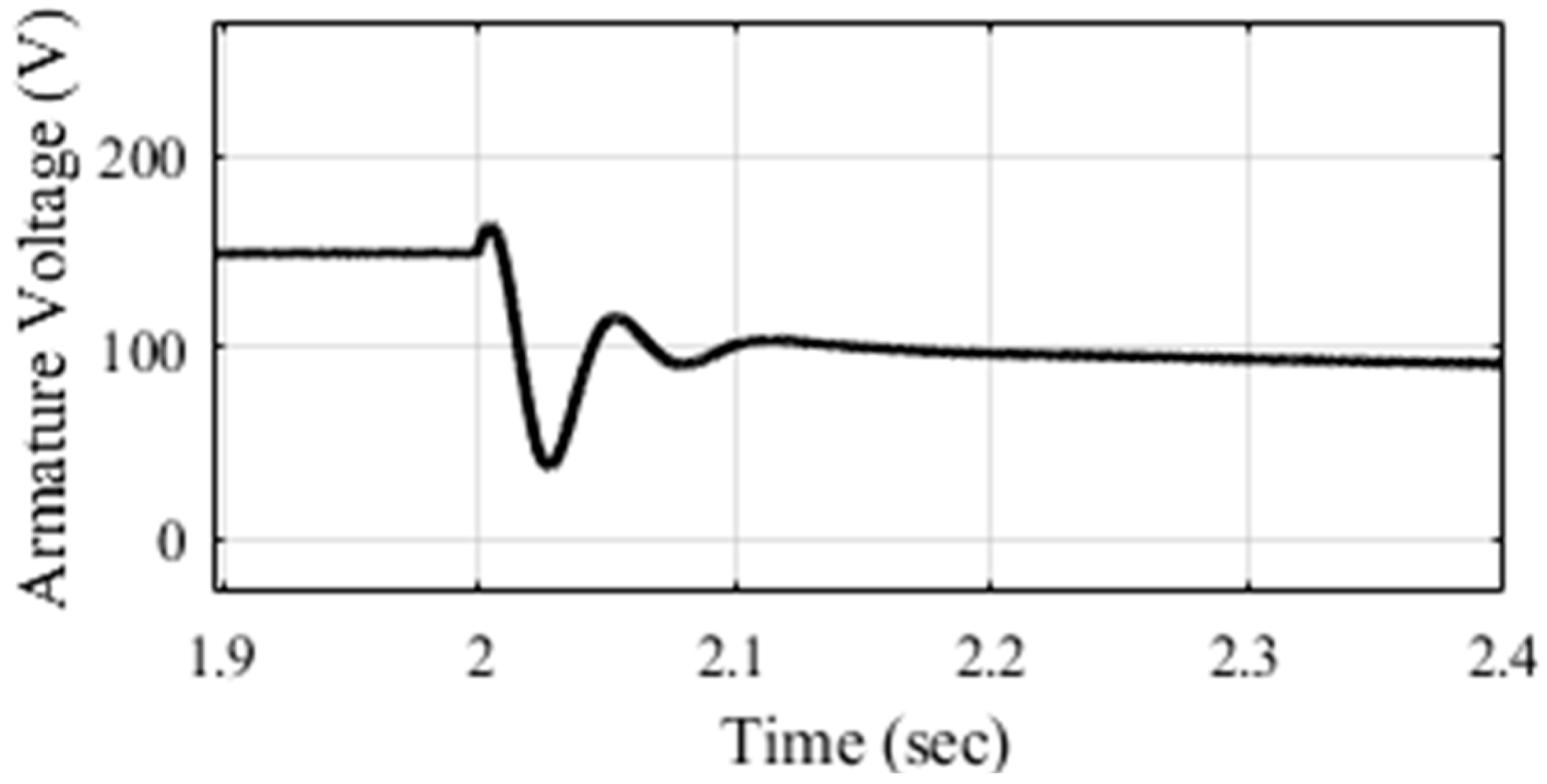
4.2. Energy Recovery Through Regenerative Braking Using FoPID Controllers
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Al-Shariff, S.M.; Alam, M.S.; Ahmad, Z.; Ahmad, F. Smart transportation system: Mobility solution for smart cities. In 2nd Smart Cities Symposium (SCS 2019); IET: Stevenage, UK, 2019; pp. 6–59. [Google Scholar]
- Leviakangas, P.; Kinnunen, T.; Kess, P. The electric vehicles ecosystem model-construct, analysis and identification of key challenges. Manag. Glob. Transit. 2014, 12, 253–277. [Google Scholar]
- Mohanraj, D.; Gopalakrishnan, J.; Chokkalingam, B.; Mihet-Popa, L. Critical aspects of electric motor drive controllers and mitigation of torque ripple—Review. IEEE Access 2022, 10, 73635–73674. [Google Scholar] [CrossRef]
- Tuttle, D.P.; Baldick, R. The evolution of plug-in electric vehicle-grid interactions. IEEE Trans. Smart Grid 2012, 3, 500–505. [Google Scholar] [CrossRef]
- Ogura, K. Kolhe Battery Technology for Electric Vehicle; Kawasaki Heavy Industries, Ltd.: Kobe, Japan; University of Agder: Kristiansand, Norway, 2017. [Google Scholar]
- Adedeji, B.P. Electric vehicles survey and a multifunctional artificial neural network for predicting energy consumption in all-electric vehicles. Results Eng. 2023, 19, 101283. [Google Scholar] [CrossRef]
- Naqvi, S.S.A.; Jamil, H.; Iqbal, N.; Khan, S.; Lee, D.I.; Park, Y.C.; Kim, D.H. Multi-objective optimization of PI controller for BLDC motor speed control and energy saving in Electric Vehicles: A constrained swarm-based approach. Energy Rep. 2024, 12, 402–417. [Google Scholar] [CrossRef]
- da Dantas, A.D.O.S.; de Dantas, A.F.O.A.; Campos, J.T.L.S.; de Almeida Neto, D.L.; Dórea, C.E.T. PID control for electric vehicles subject to control and speed signal constraints. J. Control Sci. Eng. 2018, 2018, 6259049. [Google Scholar] [CrossRef]
- Baidya, D.; Dhopte, S.; Bhattacharjee, M. Sensing System Assisted Novel PID Controller for Efficient Speed Control of DC Motors in Electric Vehicles. IEEE Sens. Lett. 2023, 7, 1–4. [Google Scholar] [CrossRef]
- Feng, N.; Yong, J.; Zhan, Z. A direct multiple shooting method to improve vehicle handling and stability for four hub-wheel-drive electric vehicle during regenerative braking. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 1047–1056. [Google Scholar] [CrossRef]
- Geng, C.; Ning, D.; Guo, L.; Xue, Q.; Mei, S. Simulation research on regenerative braking control strategy of hybrid electric vehicle. Energies 2021, 14, 2202. [Google Scholar] [CrossRef]
- Aksjonov, A.; Ricciardi, V.; Augsburg, K.; Vodovozov, V.; Petlenkov, E. Hardware-in-the-Loop test of an Open-Loop fuzzy control method for decoupled Electrohydraulic Antilock braking system. IEEE Trans. Fuzzy Syst. 2021, 29, 965–975. [Google Scholar] [CrossRef]
- Lv, C.; Zhang, J.; Li, Y.; Yuan, Y. Mechanism analysis and evaluation methodology of regenerative braking contribution to energy efficiency improvement of electrified vehicles. Energy Convers. Manag. 2015, 92, 469–482. [Google Scholar] [CrossRef]
- Li, L.; Li, X.; Wang, X.; Liu, Y.; Song, J.; Ran, X. Transient switching control strategy from regenerative braking to anti-lock braking with a semi-brake-by-wire system. Veh. Syst. Dyn. 2016, 54, 231–257. [Google Scholar] [CrossRef]
- Jamadar, N.M.; Jadhav, H.T. A review on braking control and optimization techniques for electric vehicle. Proc. Inst. Mech. Eng.-Part D J. Automob. Eng. 2021, 235, 2371–2382. [Google Scholar] [CrossRef]
- Vodovozov, V.; Raud, Z.; Petlenkov, E. Review on braking energy management in electric vehicles. Energies 2021, 14, 4477. [Google Scholar] [CrossRef]
- Ivanov, V.; Savitski, D.; Shyrokau, B. A Survey of traction control and Antilock braking systems of full electric vehicles with Individually controlled electric motors. IEEE Trans. Veh. Technol. 2015, 64, 3878–3896. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Y.; Hu, M.; Yang, Z.; Fu, C. Longitudinal-vertical comprehensive control for four-wheel drive pure electric vehicle considering energy recovery and ride comfort. Energy 2021, 236, 121417. [Google Scholar] [CrossRef]
- Saleem, O.; Rizwan, M.; Khizar, A.; Ahmad, A. Augmentation of Fractional-Order PI Controller with Nonlinear Error-Modulator for Enhancing Robustness of DC-DC Boost Converters. J. Power Electron. 2019, 19, 835–845. [Google Scholar] [CrossRef]
- Saleem, O.; Ali, S.; Iqbal, J. Robust MPPT Control of Stand-Alone Photovoltaic Systems via Adaptive Self-Adjusting Fractional Order PID Controller. Energies 2023, 16, 5039. [Google Scholar] [CrossRef]
- Saleem, O.; Shami, U.T.; Mahmood-ul-Hasan, K. Time-optimal control of DC-DC buck converter using single-input fuzzy augmented fractional-order PI controller. Int. Trans. Electr. Energy Syst. 2019, 29, e12064. [Google Scholar] [CrossRef]
- Sinha, D.; Ghosh, S.; Majumdar, S.; Bandyopadhyay, C.; Bhattacharya, S. Effective Control of Speed and Regenerative Braking in Electric Vehicles Utilizing Fractional Order PI Controller. In Proceedings of the 2025 IEEE 1st International Conference on Smart and Sustainable Developments in Electrical Engineering (SSDEE), Dhanbad, India, 28 February–2 March 2025; IEEE, 2025; pp. 1–6. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Jaber, M.M.; Jameel, S.S.; Khudhair, H.N. An Arithmetic Optimization Algorithm-Based Harris Hawks Optimization for Global Optimization. Machines 2022, 10, 602. [Google Scholar]
- Pal, S.; Sinha, D.; Das Mahapatra, M.; Majumder, S.; Bhattacharya, S.; Bandyopadhyay, C. Performance evaluation of multi-Input Interleaved Boost Converter with tuned PI controller. Chin. J. Electr. Eng. 2024, 10, 119–128. [Google Scholar] [CrossRef]
- Sinha, D.; Mahapatra, M.D.; Pal, S.; Majumder, S.; Bhattacharya, S.; Bandyopadhyay, C. Adaptation of fractional-order PI controller for a variable input interleaved DC–DC boost converter using particle swarm optimization with parametric variation. IFAC J. Syst. Control 2025, 32, 100301. [Google Scholar] [CrossRef]








| Battery Specification | |
|---|---|
| Type of Battery | Lithium Ferro Phosphate |
| Nominal voltage (V) | 72 |
| Rated capacity (Ah) | 400 |
| Initial state of charge (% SOC) | 50 |
| Cut-off voltage (V) | 54 |
| Fully charged voltage (V) | 78.4 |
| Nominal discharge current (A) | 30 |
| Internal resistance (Ohms) | 0.0048 |
| Capacity (Ah) at nominal voltage | 46.54 |
| DC–DC Interleaved Boost Chopper Specification (For Battery Charging) | |
| Output Power rating (kW) | 24 |
| Operating Frequency (kHz) | 5 |
| Inductance (H) | 0.0199 |
| Capacitance (uF) | 312 |
| Output voltage (V) | 600 |
| Output current (A) | 40 |
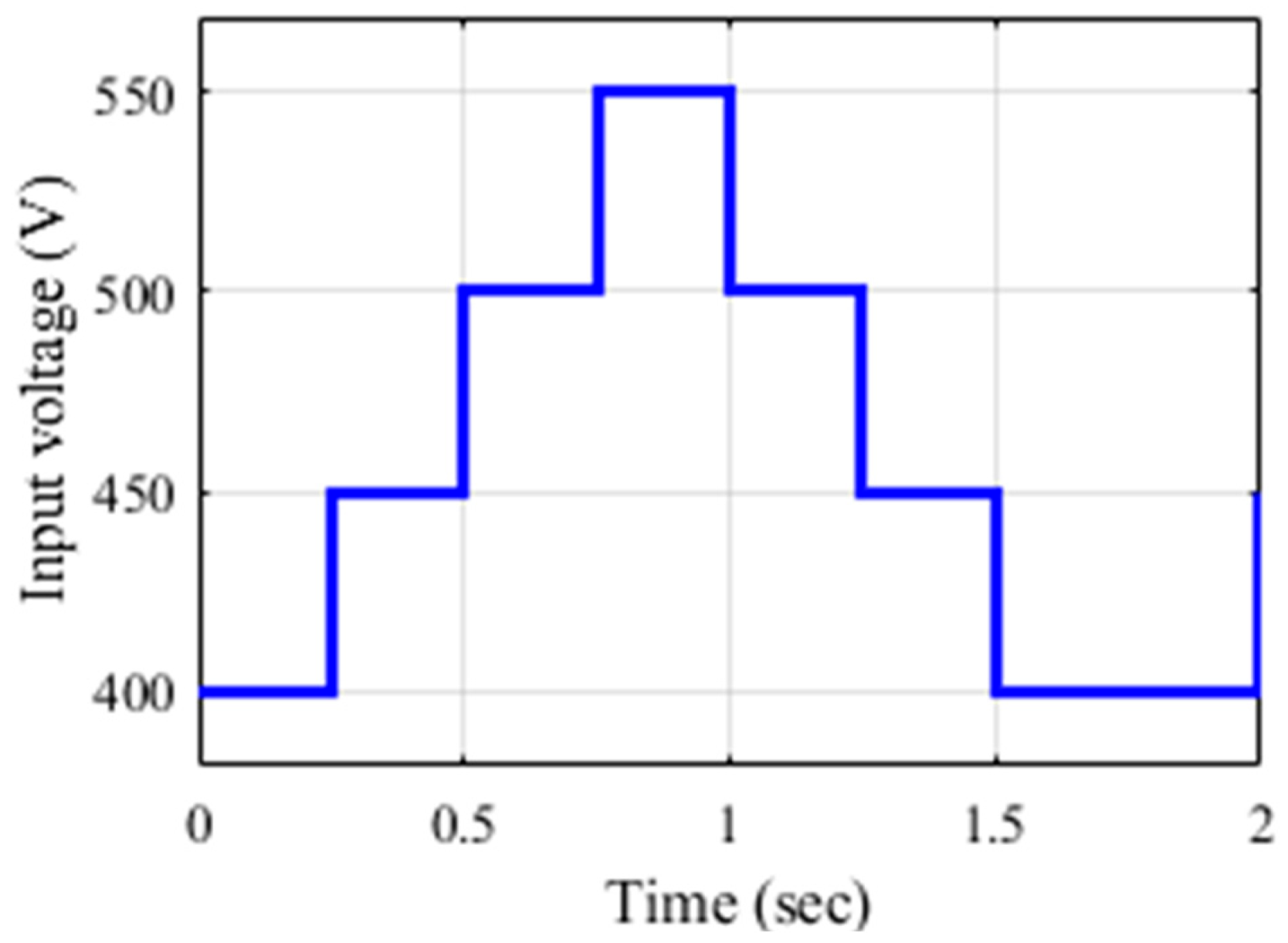
| Input voltage variation (V) | 400–550 |
| Synchronous Boost Chopper Specification (For Regenerative Braking) | |
| Inductance (H) | 0.03 |
| Input filter capacitance (mF) | 2.9 |
| Output filter capacitance (mF) | 2.9 |
| Initial voltage stored at output capacitance (V) | 240 |
| 3-phase BLDC Motor Specification | |
| Stator-phase resistance (Ohm) | 0.47 |
| Stator-phase induction (H) | 0.000595 |
| Inertia constant | 0.0003 |
| Viscous damping | 0.00030345 |
| Pole pair | 4 |
| Rotor flux position when Theta = 0 | 90° behind-phase-A (modified park) transformation |
| Category | Parameters | Values |
|---|---|---|
| PI controller | Range: 0.0001–100 | |
| Search space | Lower and upper bounds | [0.0001, 0.0001], [100, 100] |
| AHHO setup | Population size | 30 |
| Max iterations | 100 | |
| Random coefficients | ||
| Optimization logic | From 1 to −1 over iterations | |
| Objective | Fitness function | IAE |
| Constraints | ||||
|---|---|---|---|---|
| Method | % Mp | Ts (s) | Treach (s) (Initial) | Treach (s) (Intermediate) |
| PI-ZN | 13.33 | 0.09 | 0.1563 | 0.0938 |
| PI-AHHO | 8.33 | 0.06 | 0.1 | 0.065 |
| FoPI-AHHO | 5.0 | 0.03 | 0.0625 | 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinha, D.; Majumder, S.; Bandyopadhyay, C.; Sharma, H.K. Arithmetic Harris Hawks-Based Effective Battery Charging from Variable Sources and Energy Recovery Through Regenerative Braking in Electric Vehicles, Implying Fractional Order PID Controller. Fractal Fract. 2025, 9, 525. https://doi.org/10.3390/fractalfract9080525
Sinha D, Majumder S, Bandyopadhyay C, Sharma HK. Arithmetic Harris Hawks-Based Effective Battery Charging from Variable Sources and Energy Recovery Through Regenerative Braking in Electric Vehicles, Implying Fractional Order PID Controller. Fractal and Fractional. 2025; 9(8):525. https://doi.org/10.3390/fractalfract9080525
Chicago/Turabian StyleSinha, Dola, Saibal Majumder, Chandan Bandyopadhyay, and Haresh Kumar Sharma. 2025. "Arithmetic Harris Hawks-Based Effective Battery Charging from Variable Sources and Energy Recovery Through Regenerative Braking in Electric Vehicles, Implying Fractional Order PID Controller" Fractal and Fractional 9, no. 8: 525. https://doi.org/10.3390/fractalfract9080525
APA StyleSinha, D., Majumder, S., Bandyopadhyay, C., & Sharma, H. K. (2025). Arithmetic Harris Hawks-Based Effective Battery Charging from Variable Sources and Energy Recovery Through Regenerative Braking in Electric Vehicles, Implying Fractional Order PID Controller. Fractal and Fractional, 9(8), 525. https://doi.org/10.3390/fractalfract9080525






