Unsupervised Multimodal Community Detection Algorithm in Complex Network Based on Fractal Iteration
Abstract
1. Introduction
- 1.
- A novel unsupervised node feature aggregation method is designed based on fractal iteration principles. This method avoids introducing nonlinear functions or adjustable parameters. Through multi-layer iteration, each node’s final representation effectively integrates information from all nodes within its multi-hop neighborhood.
- 2.
- A semantic–structural dual-channel encoder (DC-SSE) is proposed, which fuses semantic features—obtained by reducing the dimensionality of PFGC-derived features via UMAP—with structural features extracted by PFGC to produce the final node embeddings.
- 3.
- The fused node representations obtained from the dual-channel encoder are clustered using the K-means algorithm, achieving superior community partitioning results compared to traditional methods.
2. Related Work
2.1. Spectral Clustering-Based Community Detection Methods
2.2. Modularity Optimization-Based Community Detection Methods
2.3. Graph Neural Network-Based Community Detection Methods
2.4. Core-Expansion-Based Community Detection Methods
2.5. Semi-Supervised Community Detection Methods
2.6. Other Community Detection Methods
2.7. Fractals and Community Detection
3. Methodology
3.1. Unsupervised Node Feature Aggregation Method
| Algorithm 1. Parameter-free graph convolution algorithm. |
| Input: Network , Initial node features Parameters: Number of layers , Anti-over-smoothing coefficient |
| Output: Graph convolution encoded features: Begin |
|
| End |
3.2. Semantic–Structural Dual-Channel Encoder
3.2.1. Semantic Encoder
| Algorithm 2. UMAP-based semantic encoder. |
| Input: Input features , Target dimension Parameters: Neighborhood parameter , minimum distance parameter , learning rate , number of iterations |
| Output: Semantic encoded features: BEGIN |
|
|
| END |
3.2.2. Structural Encoder
| Algorithm 3. Structural diagram of convolutional encoder. |
| Input: Network , initial node features Parameters: Number of iterations |
| Output: Output feature Begin |
|
| End |
4. Experiments
4.1. Experimental Setup
4.1.1. Experimental Datasets
- 1.
- Classic Small-Scale Networks
- 2.
- Large-Scale Real-World Networks
- 3.
- Citation Network Datasets
4.1.2. Evaluation Metrics
4.1.3. Hyperparameter Configuration
4.2. Baseline Algorithms
- 1.
- Unsupervised Methods
- 2.
- Supervised Methods
4.3. Experimental Results on Small-Scale Real-World Datasets
4.3.1. NMI Results on Small-Scale Real-World Datasets
4.3.2. Visualization of Community Detection Results on Small-Scale Real-World Datasets
4.4. Experimental Results on Large-Scale Real-World Networks
4.5. Effectiveness Analysis of the Parameter-Free GCN Encoder
4.5.1. Visualization Analysis of Encoder Results
4.5.2. Quantitative Analysis of Encoder Effectiveness
4.6. Ablation Study
4.6.1. Module-Level Ablation Study
4.6.2. Parameter Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Alamsyah, A.; Rahardjo, B. Community detection methods in social network analysis. Adv. Sci. Lett. 2014, 20, 250–253. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Fortunato, S.; Kertész, J. Detecting the overlapping and hierarchical community structure in complex networks. New J. Phys. 2009, 11, 033015. [Google Scholar] [CrossRef]
- Rahiminejad, S.; Maurya, M.R.; Subramaniam, S. Topological and functional comparison of community detection algorithms in biological networks. BMC Bioinform. 2019, 20, 212. [Google Scholar] [CrossRef]
- Akoglu, L.; Tong, H.; Koutra, D. Graph based anomaly detection and description: A survey. Data Min. Knowl. Discov. 2015, 29, 626–688. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, D.; Yildirim, M.Y.; Alcorn, S.; He, J.; Davulcu, H.; Tong, H. Hidden: Hierarchical dense subgraph detection with application to financial fraud detection. In Proceedings of the SIAM International Conference on Data Mining, Houston, TX, USA, 27–29 April 2017. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Zhou, D.; Zhang, S.; Yildirim, M.Y.; Alcorn, S.; Tong, H.; Davulcu, H.; He, J. A local algorithm for structure-preserving graph cut. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017. [Google Scholar]
- Sobolevsky, S.; Belyi, A. Graph neural network inspired algorithm for unsupervised network community detection. Appl. Netw. Sci. 2022, 7, 63. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar] [CrossRef]
- Ng, A.; Jordan, M.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Proceedings of the 14th Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 3–8 December 2001. [Google Scholar]
- Dhillon, I.S.; Guan, Y.; Kulis, B. Weighted graph cuts without eigenvectors: A multilevel approach. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1944–1957. [Google Scholar] [CrossRef]
- Zelnik-Manor, L.; Perona, P. Self-tuning spectral clustering. In Proceedings of the 17th Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 13–18 December 2004. [Google Scholar]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Reichardt, J.; Bornholdt, S. Statistical mechanics of community detection. Phys. Rev. E 2006, 74, 016110. [Google Scholar] [CrossRef] [PubMed]
- Que, X.; Checconi, F.; Petrini, F.; Gunnels, J.A. Scalable community detection with the Louvain algorithm. In Proceedings of the IEEE International Parallel and Distributed Processing Symposium, Hyderabad, India, 25–29 May 2015. [Google Scholar]
- Pons, P.; Latapy, M. Computing communities in large networks using random walks. In Computer and Information Sciences—ISCIS 2005, 1st ed.; Yolum, P., Güngör, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 284–293. [Google Scholar]
- Mucha, P.J.; Richardson, T.; Macon, K.; Porter, M.A.; Onnela, J.P. Community structure in time-dependent, multiscale, and multiplex networks. Science 2010, 328, 876–878. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 30th Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Xu, X.; Yuruk, N.; Feng, Z.; Schweiger, T.A.J. SCAN: A Structural Clustering Algorithm for Networks. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, CA, USA, 12–15 August 2007; pp. 824–833. [Google Scholar]
- Palla, G.; Derényi, I.; Farkas, I.; Vicsek, T. Uncovering the Overlapping Community Structure of Complex Networks in Nature and Society. Nature 2005, 435, 814–818. [Google Scholar] [CrossRef]
- Coscia, M.; Rossetti, G.; Giannotti, F.; Pedreschi, D. DEMON: A Local-First Discovery Method for Overlapping Communities. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 615–623. [Google Scholar]
- Zhu, X.; Ghahramani, Z.; Lafferty, J.D. Semi-supervised learning using gaussian fields and harmonic functions. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 888–895. [Google Scholar]
- Raghavan, U.N.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in large-scale networks. Phys. Rev. E 2007, 76, 036106. [Google Scholar] [CrossRef]
- Xie, J.; Szymanski, B.K. Towards linear time overlapping community detection in social networks. In Advances in Knowledge Discovery and Data Mining, 1st ed.; Tan, P.-N., Chawla, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 25–36. [Google Scholar]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph Regularized Nonnegative Matrix Factorization for Data Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1548–1560. [Google Scholar]
- Lee, H.; Yoo, J.; Choi, S. Semi-supervised nonnegative matrix factorization. IEEE Signal Process. Lett. 2009, 17, 4–7. [Google Scholar] [CrossRef]
- He, C.; Liu, X.; Yu, P.; Liu, C.; Hu, Y. Community detection method based on robust semi-supervised nonnegative matrix factorization. Phys. A Stat. Mech. Its Appl. 2019, 523, 279–291. [Google Scholar] [CrossRef]
- Ma, X.; Dong, D.; Wang, Q. Community detection in multi-layer networks using joint nonnegative matrix factorization. IEEE Trans. Knowl. Data Eng. 2018, 31, 273–286. [Google Scholar] [CrossRef]
- Rosvall, M.; Bergstrom, C.T. Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. USA 2008, 105, 1118–1123. [Google Scholar] [CrossRef]
- Karrer, B.; Newman, M.E.J. Stochastic blockmodels and community structure in networks. Phys. Rev. E 2011, 83, 016107. [Google Scholar] [CrossRef]
- Arenas, A.; Díaz-Guilera, A.; Pérez-Vicente, C.J. Synchronization reveals topological scales in complex networks. Phys. Rev. Lett. 2006, 96, 114102. [Google Scholar] [CrossRef]
- Lambiotte, R.; Delvenne, J.C.; Barahona, M. Random walks, Markov processes and the multiscale modular organization of complex networks. IEEE Trans. Netw. Sci. Eng. 2015, 1, 76–90. [Google Scholar] [CrossRef]
- Pizzuti, C. GA-Net: A genetic algorithm for community detection in social networks. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Dortmund, Germany, 13–17 September 2008. [Google Scholar]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Cannon, J.W. The fractal geometry of nature. by Benoit B. Mandelbrot. Am. Math. Mon. 1984, 91, 594–598. [Google Scholar] [CrossRef]
- Song, C.; Havlin, S.; Makse, H.A. Self-similarity of complex networks. Nature 2005, 433, 392–395. [Google Scholar] [CrossRef]
- Song, C.; Gallos, L.K.; Havlin, S.; Makse, H.A. How to calculate the fractal dimension of a complex network: The box covering algorithm. J. Stat. Mech. 2007, 2007, P03006. [Google Scholar] [CrossRef]
- Rozenfeld, H.D.; Song, C.; Makse, H.A. Small-world to fractal transition in complex networks: A renormalization group approach. Phys. Rev. Lett. 2010, 104, 025701. [Google Scholar] [CrossRef]
- Ye, Z.; Li, Z.; Li, G.; Zhao, H. Dual-channel deep graph convolutional neural networks. Front. Artif. Intell. 2024, 7, 1290491. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Zhang, Y. Multi-modal Graph Neural Network for Attributed Network Embedding. Knowl.-Based Syst. 2024, 283, 111234. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. [Google Scholar] [CrossRef]
- Douady, A.; Hubbard, J.H. On the dynamics of polynomial-like mappings. Ann. Sci. Ec. Norm. Super. 1985, 18, 287–343. [Google Scholar] [CrossRef]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications, 3rd ed.; John Wiley & Sons: Chichester, UK, 2013; pp. 27–29. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. Available online: https://arxiv.org/abs/1802.03426 (accessed on 21 June 2025).
- Zachary, W.W. An information flow model for conflict and fission in small groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar] [CrossRef]
- Lusseau, D.; Schneider, K.; Boisseau, O.J.; Haase, P.; Slooten, E.; Dawson, S.M. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations: Can geographic isolation explain this unique trait? Behav. Ecol. Sociobiol. 2003, 54, 396–405. [Google Scholar] [CrossRef]
- Evans, T.S. Clique graphs and overlapping communities. J. Stat. Mech. 2010, 2010, P12037. [Google Scholar] [CrossRef]
- Pasternak, B.; Ivask, I. Four unpublished letters. Books Abroad 1970, 44, 196–200. [Google Scholar] [CrossRef]
- Yang, J.; Leskovec, J. Defining and evaluating network communities based on ground-truth. In Proceedings of the ACM SIGKDD Workshop on Mining Data Semantics, Beijing, China, 12–16 August 2012. [Google Scholar]
- Sen, P.; Namata, G.; Bilgic, M.; Getoor, L.; Galligher, B.; Eliassi-Rad, T. Collective classification in network data. AI Mag. 2008, 29, 93. [Google Scholar] [CrossRef]
- De Meo, P.; Ferrara, E.; Fiumara, G.; Provetti, A. Mixing local and global information for community detection in large networks. J. Comput. Syst. Sci. 2014, 80, 72–87. [Google Scholar] [CrossRef]
- Yang, J.; Leskovec, J. Overlapping community detection at scale: A nonnegative matrix factorization approach. In Proceedings of the Sixth ACM International Conference on Web Search and Data Mining, Rome, Italy, 4–8 February 2013. [Google Scholar]
- Al-Andoli, M.; Cheah, W.P.; Tan, S.C. Deep learning-based community detection in complex networks with network partitioning and reduction of trainable parameters. J. Ambient Intell. Humaniz. Comput. 2021, 12, 2527–2545. [Google Scholar] [CrossRef]
- Yang, L.; Cao, X.; He, D.; Wang, C.; Wang, X.; Zhang, W. Modularity based community detection with deep learning. In Proceedings of the 25th International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016. [Google Scholar]
- Cai, B.; Wang, Y.; Zeng, L.; Hu, Y.; Li, H. Edge classification based on convolutional neural networks for community detection in complex network. Physica A 2020, 556, 124826. [Google Scholar] [CrossRef]
- Cai, B.; Wang, M.; Chen, Y.; Hu, Y.; Liu, M. MFF-Net: A multi-feature fusion network for community detection in complex network. Knowl.-Based Syst. 2022, 252, 109408. [Google Scholar] [CrossRef]
- Qiu, C.; Huang, Z.; Xu, W.; Li, H. VGAER: Graph neural network reconstruction based community detection. arXiv 2022, arXiv:2201.04066. [Google Scholar] [CrossRef]
- Liu, B.; Wang, D.; Gao, J. A multi-objective community detection algorithm with a learning-based strategy. Int. J. Comput. Intell. Syst. 2024, 17, 311. [Google Scholar] [CrossRef]
- Yuan, S.; Wang, C.; Jiang, Q.; Ma, J. Community detection with graph neural network using Markov stability. In Proceedings of the International Conference on Artificial Intelligence in Information and Communication, Jeju Island, Republic of Korea, 21–24 February 2022. [Google Scholar]

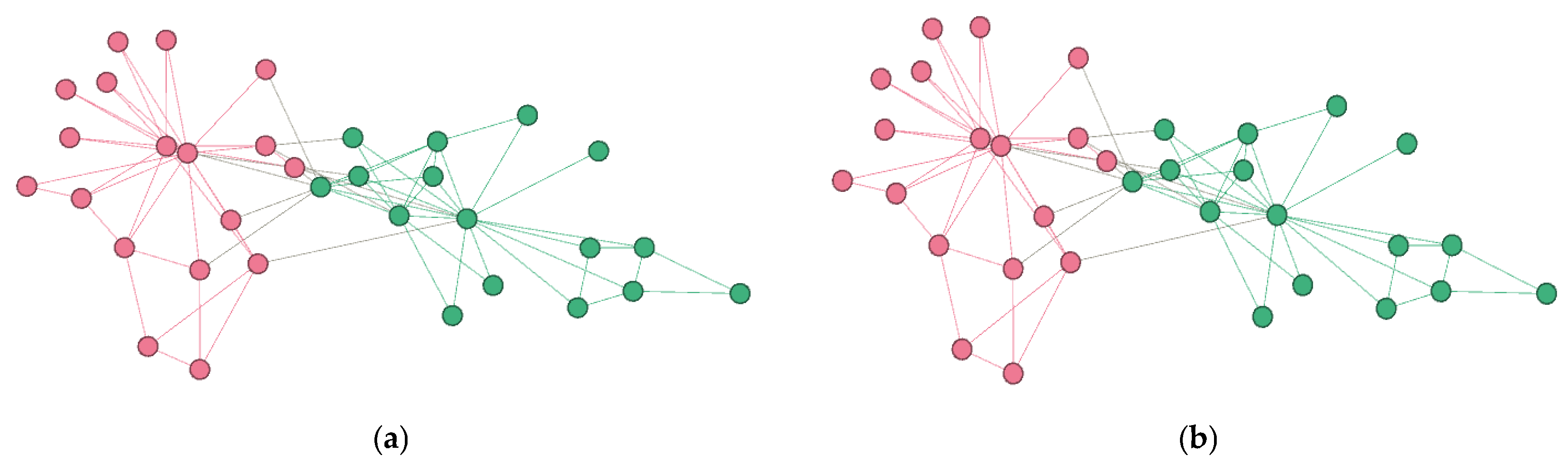

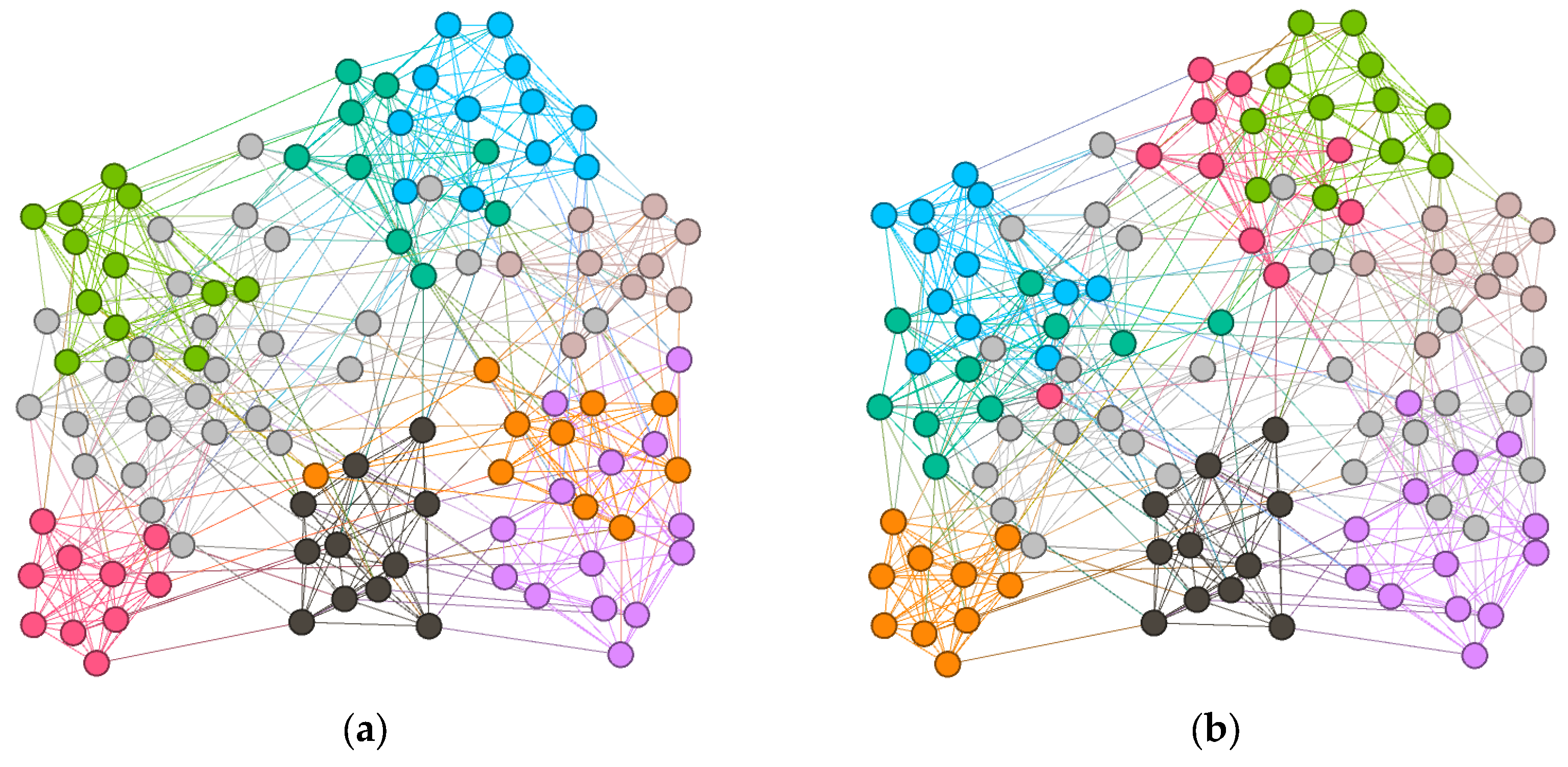
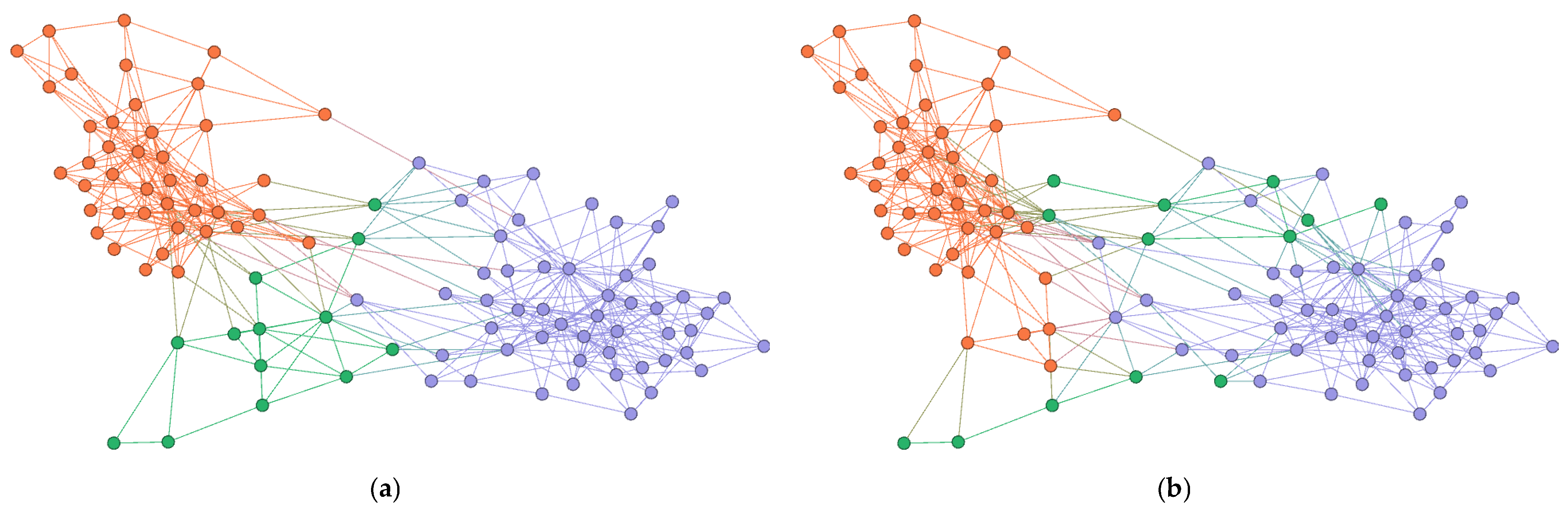


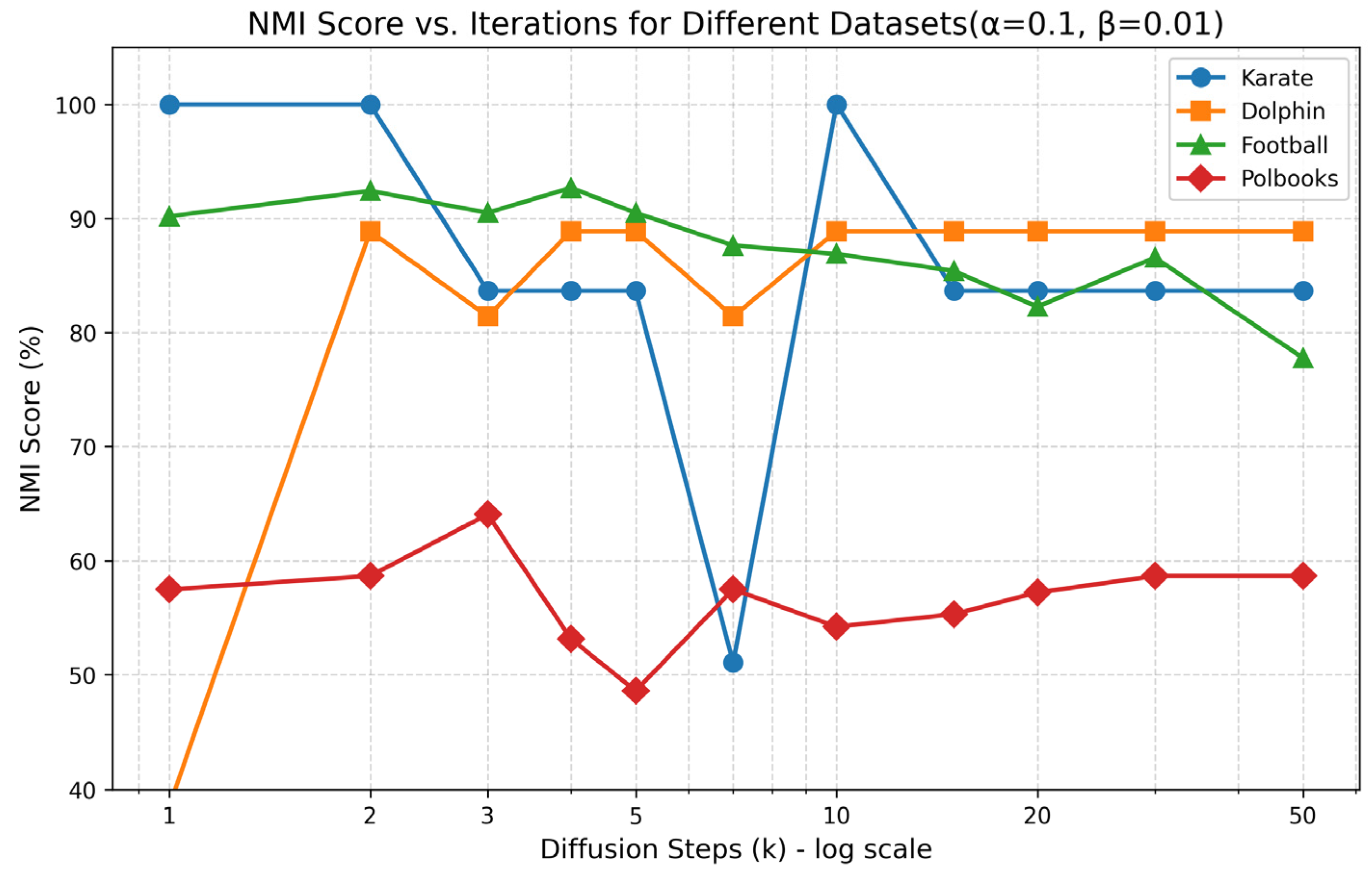
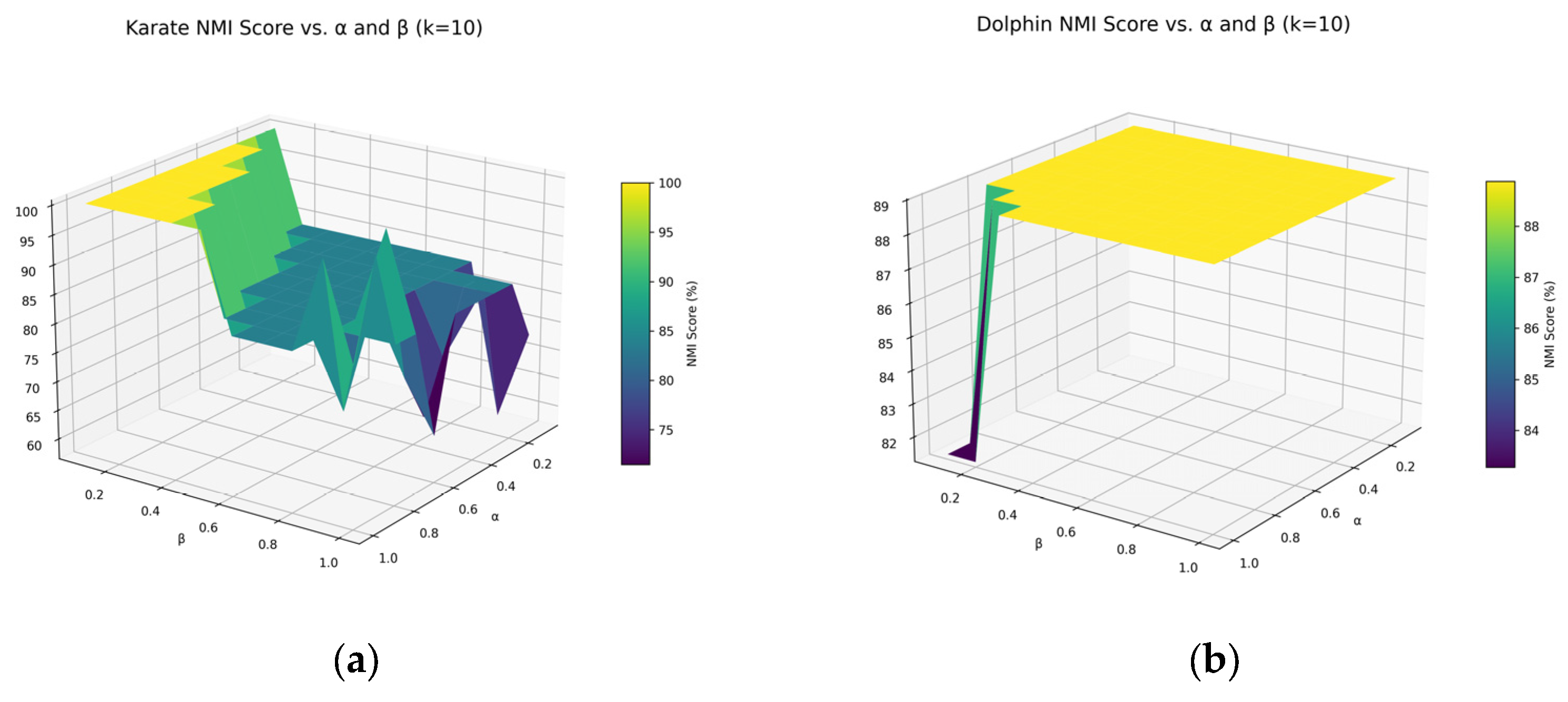
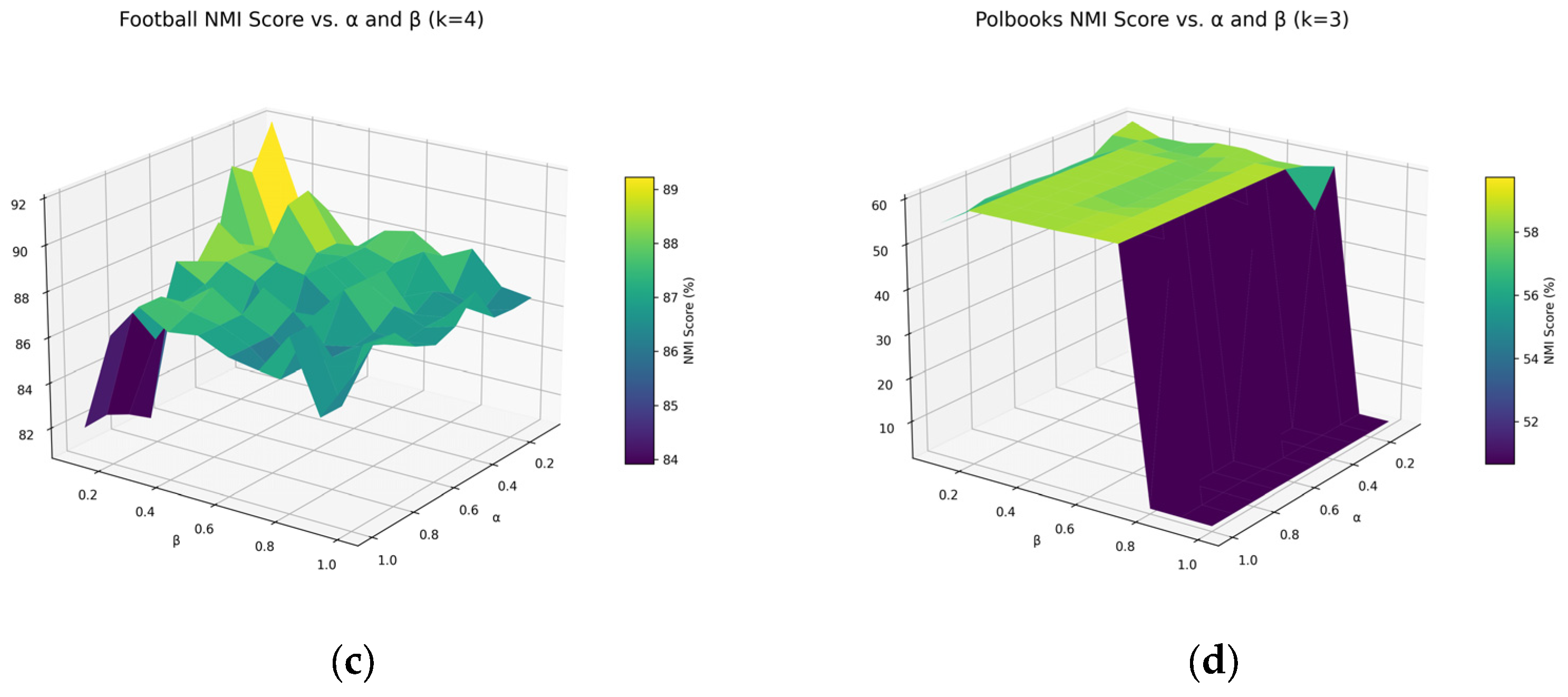
| Parameters | Karate | Dolphin | Football | PolBooks |
|---|---|---|---|---|
| 10 | 10 | 4 | 3 | |
| 4 | 4 | 24 | 12 | |
| 0.1 | 0.1 | 0.1 | 0.1 | |
| 0.01 | 0.01 | 0.01 | 0.01 | |
| 4 | 4 | 18 | 4 | |
| 22 | 10 | 6 | 74 | |
| 2 | 2 | 12 | 3 |
| Algorithm | Supervised Learning | Karate | Dolphin | Football | PolBooks |
|---|---|---|---|---|---|
| Spectral Cluster | no | 83.6 | 88.9 | 92.4 | 57.4 |
| Label Propagation | no | 44.5 | 52.7 | 87.3 | 53.4 |
| Louvain | no | 48.2 | 44.9 | 91.3 | 40.8 |
| DACDPR | yes | 100 | 87.8 | 91.4 | 57.2 |
| DNR_CE | yes | 100 | 88.9 | 91.4 | 58.2 |
| ComNet-R | yes | 100 | 88.9 | 91.4 | 59.8 |
| MFF-NET | yes | 100 | 100 | 92.4 | 63.2 |
| VGAER | yes | 100 | 91.9 | 87.3 | - |
| LSCD | no | 69.1 | 62.5 | 87.9 | - |
| Ours | no | 100 | 88.9 | 92.7 | 61.4 |
| Algorithm | Supervised Learning | Amazon | DBLP | YouTube |
|---|---|---|---|---|
| BIGCLAM | no | 20.1 | 11.2 | - |
| LP-W | no | 41.3 | 25.5 | 3.2 |
| Louvain | yes | 43.0 | 28.0 | 4.3 |
| Louvain-W | yes | 42.4 | 26.8 | 5.1 |
| GraphGAN | yes | 41.7 | 8.3 | 4.9 |
| ComNet-R | yes | 46.8 | 44.8 | 22.4 |
| MFF | yes | 47.2 | 57.6 | 37.3 |
| CDMG | no | 11.4 | 24.5 | 16.5 |
| Ours | no | 47.9 | 60.4 | 32.7 |
| Algorithm | CiteSeer | Cora | PubMed |
|---|---|---|---|
| GCN | 67.9 ± 0.5 | 80.1 ± 0.5 | 78.9 ± 0.7 |
| PFGC | 69.0 ± 0.1 | 78.2 ± 1.0 | 78.7 ± 0.5 |
| Algorithm | Karate | Dolphin | Football | PolBooks | DBLP |
|---|---|---|---|---|---|
| RAW | 46.6 | 13.7 | 92.4 | 13.8 | 4.7 |
| PFGC | 100 | 81.4 | 92.7 | 52.9 | 51.6 |
| PFGC + DC-SSE | 100 | 88.9 | 92.7 | 61.4 | 60.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, H.; Huang, Y.; Wang, J.; Hu, Y.; Cai, B. Unsupervised Multimodal Community Detection Algorithm in Complex Network Based on Fractal Iteration. Fractal Fract. 2025, 9, 507. https://doi.org/10.3390/fractalfract9080507
Deng H, Huang Y, Wang J, Hu Y, Cai B. Unsupervised Multimodal Community Detection Algorithm in Complex Network Based on Fractal Iteration. Fractal and Fractional. 2025; 9(8):507. https://doi.org/10.3390/fractalfract9080507
Chicago/Turabian StyleDeng, Hui, Yanchao Huang, Jian Wang, Yanmei Hu, and Biao Cai. 2025. "Unsupervised Multimodal Community Detection Algorithm in Complex Network Based on Fractal Iteration" Fractal and Fractional 9, no. 8: 507. https://doi.org/10.3390/fractalfract9080507
APA StyleDeng, H., Huang, Y., Wang, J., Hu, Y., & Cai, B. (2025). Unsupervised Multimodal Community Detection Algorithm in Complex Network Based on Fractal Iteration. Fractal and Fractional, 9(8), 507. https://doi.org/10.3390/fractalfract9080507






