Joint Parameter and State Estimation of Fractional-Order Singular Systems Based on Amsgrad and Particle Filter
Abstract
1. Introduction
2. System Description
3. Algorithm Derivation
3.1. Particle Filter (PF)
3.2. Amsgrad Optimization
- Learning rate λ: Initial values should be higher for smooth problems and lower for noisy or nonlinear systems. Time decay () is implemented to balance rapid convergence in the early stage and the precise refinement in the later stage.
- First-order moment factor : For fractional-order systems with long memory effects, dynamic decay () is used to mitigate historical gradient interference. And its initial value is close to 1.
- Second-order moment factor : Maintaining with max operation of Amsgrad can prevent premature learning rate decay while preserving gradient variance information.
- Stability constant ε: Setting ε to a tiny number such as can prevent the denominator of (19) from reporting an error when the second-order moment estimate is 0.
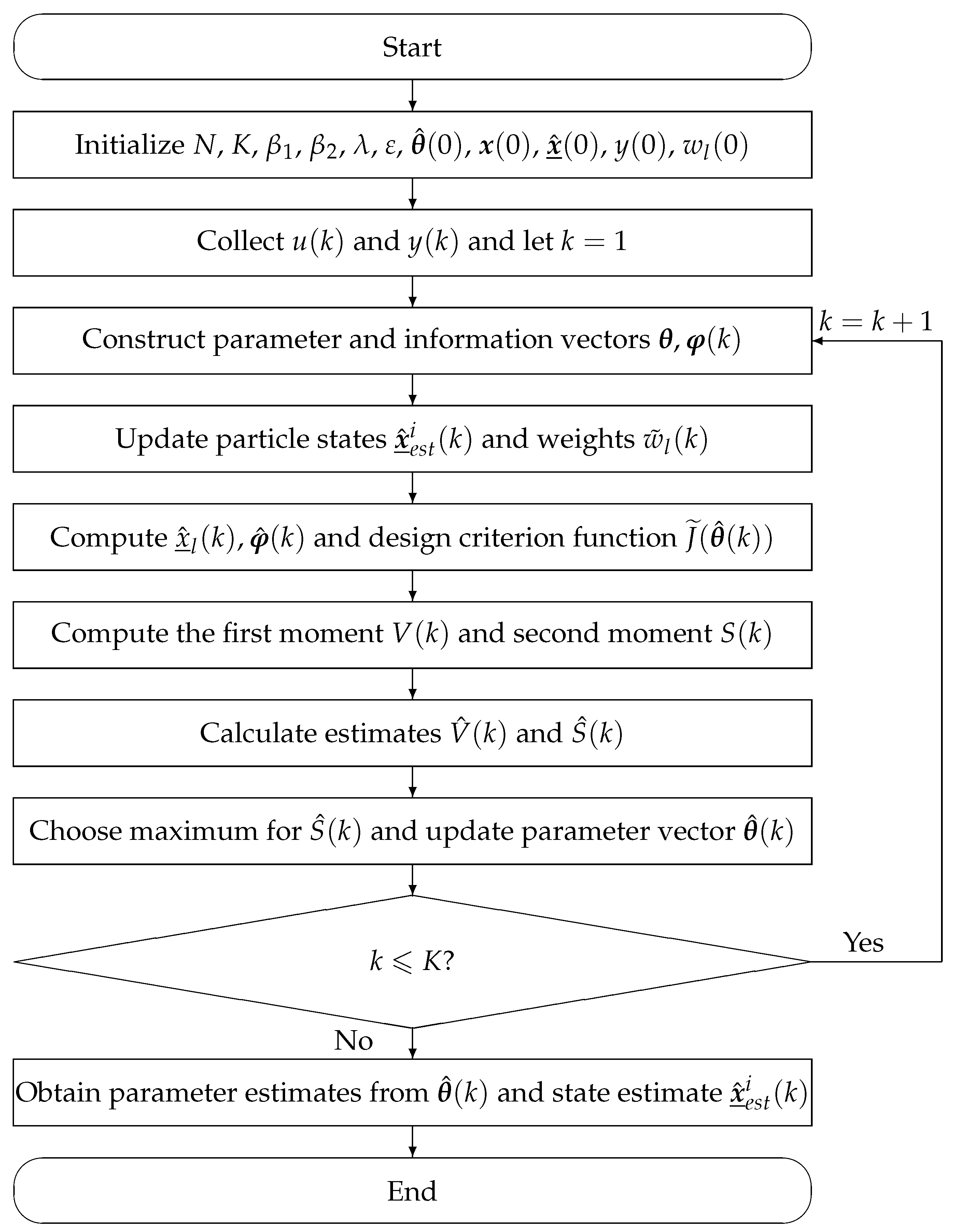
3.3. Joint Estimation Based on Amsgrad-Particle Filter (Ams-PF)
- Initialize the particle number N, the recursion count K, and set parameters and . Small initial variables are defined as , is a relatively large number.
- Collect and , then set . Construct parameter and information vectors , by (7) and (8).
- The system states based on the PF phase begins. Firstly, solutions of N particles are initialized according to (9). Then, update both the particle weights and states using (13), (20) and (21), and implement the resampling strategy. Finally, the particle weights are normalized to recursively obtain the state estimates by (22).
- In the Amsgrad optimization phase, the system parameters are optimized. Firstly, the first moment and second moment are computed using (14) and (16), respectively. The parameter estimates are updated via gradient information, ensuring the system output converges closer to the true observed values. Then, compute the bias-corrected first moment estimate by (15) and the bias-corrected second moment estimate by (17). Besides, perform the maximum value operation based on (18). Finally, calculate the estimated parameter vector by (19).
- Increase k by 1 and return to Step 3. Continue the recursive computation until k reaches the total data length K.
3.4. Convergence and Error Bound Proof of the Ams-PF Algorithm
4. Illustrative Examples
4.1. Three-Order Fractional Singular System
4.2. Four-Order Fractional Singular System
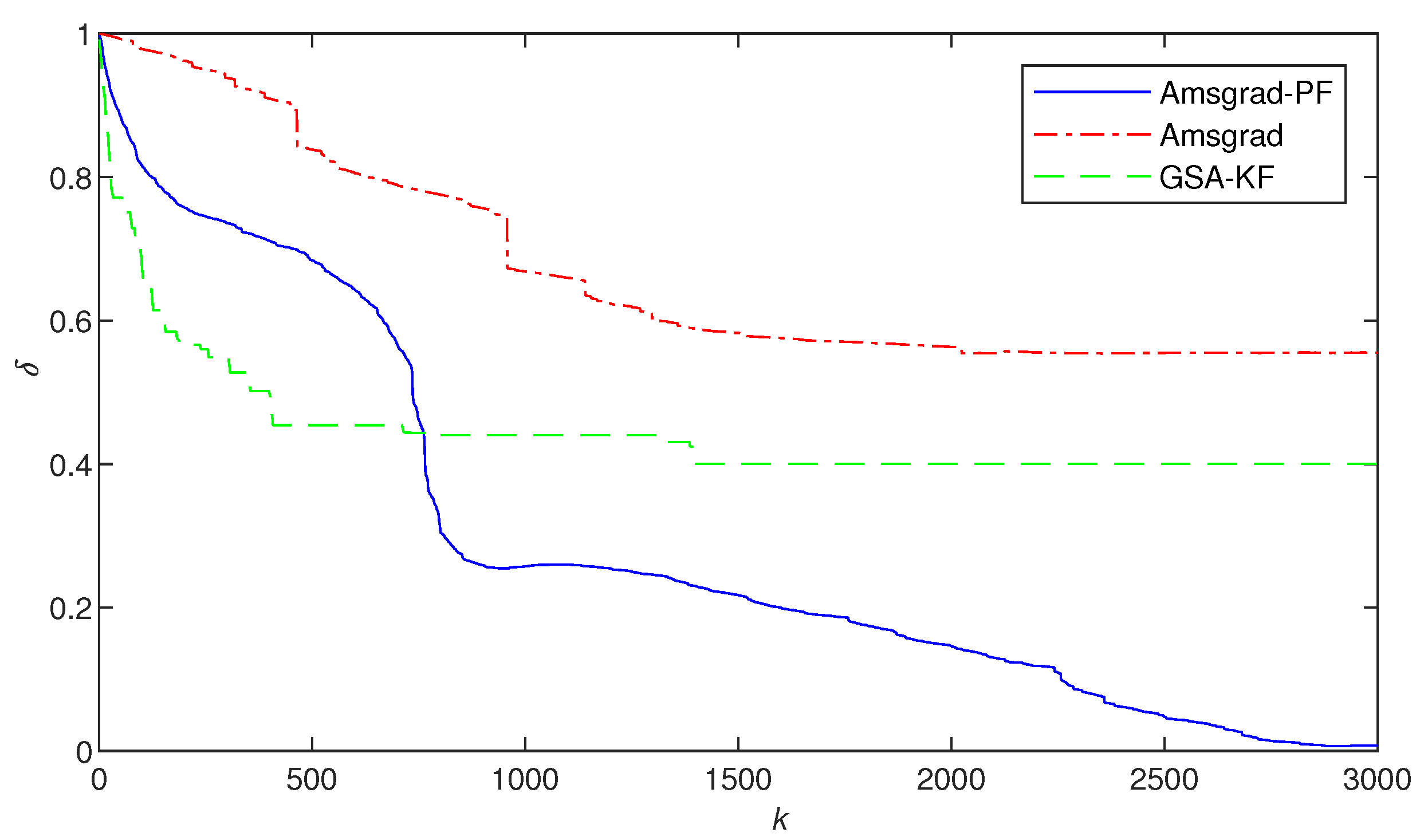
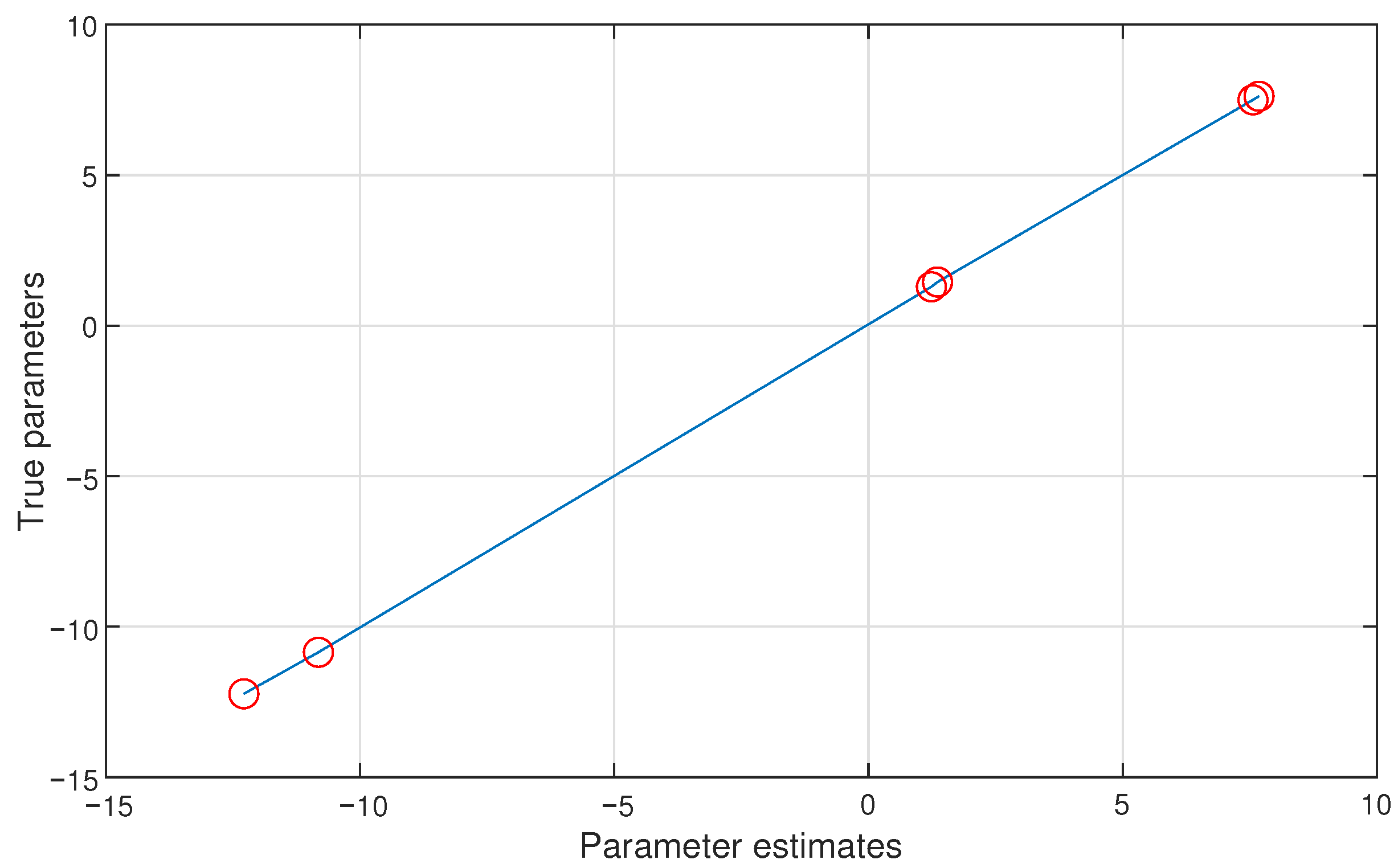
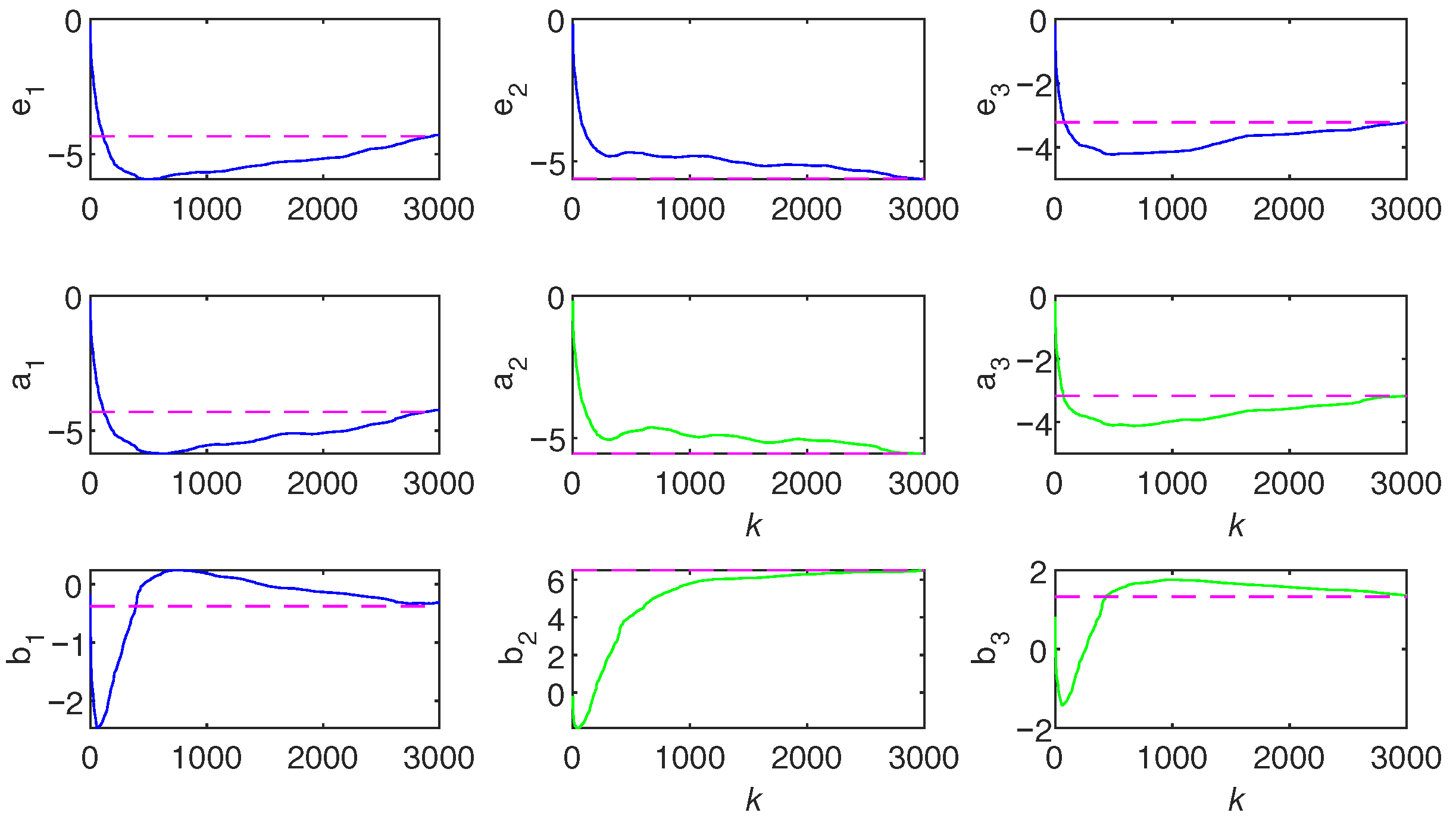
- By horizontally looking at the values in Table 1 and Table 3, it can be observed that the parameters identified by Ams-PF gradually approach the true values as k increases. It can be seen from the last line of each method that the final identification errors of Ams-PF are and , which are significantly smaller than those of the Amsgrad ( and ) and GSA-KF ( and ) methods. Thus, the Ams-PF algorithm can effectively identify fractional singular systems and its identification performance is satisfactory.
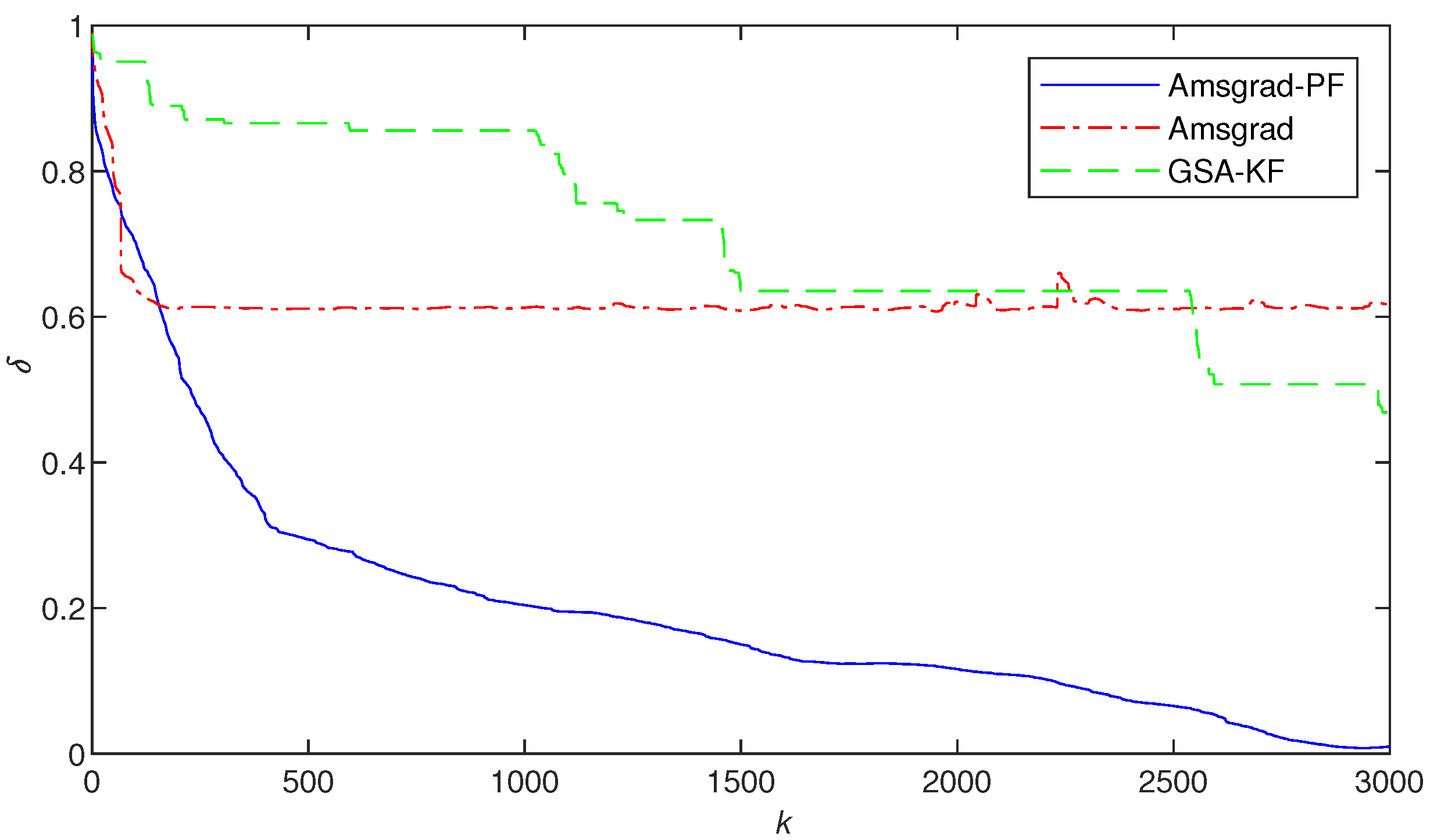
- In Figure 2, Figure 3 and Figure 4, Figure 8 and Figure 9, the Ams-PF algorithm exhibits excellent convergence speed and identification accuracy. Moreover, the system parameters identified by Ams-PF all converge near their true values with minimal estimation errors. Thus, it exhibits a stronger ability to escape local optima and has a faster convergence speed than Amsgrad and GSA-KF.
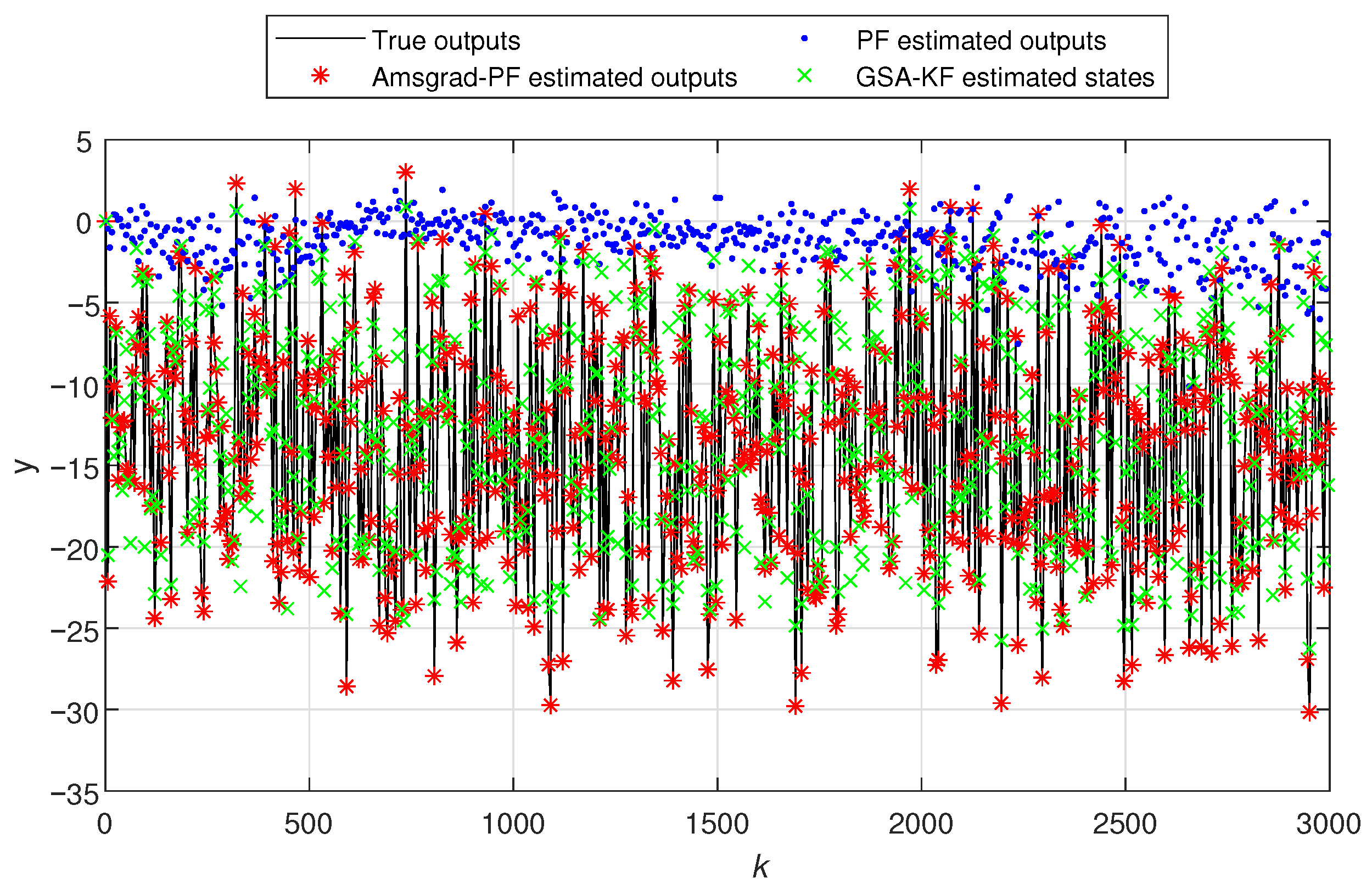
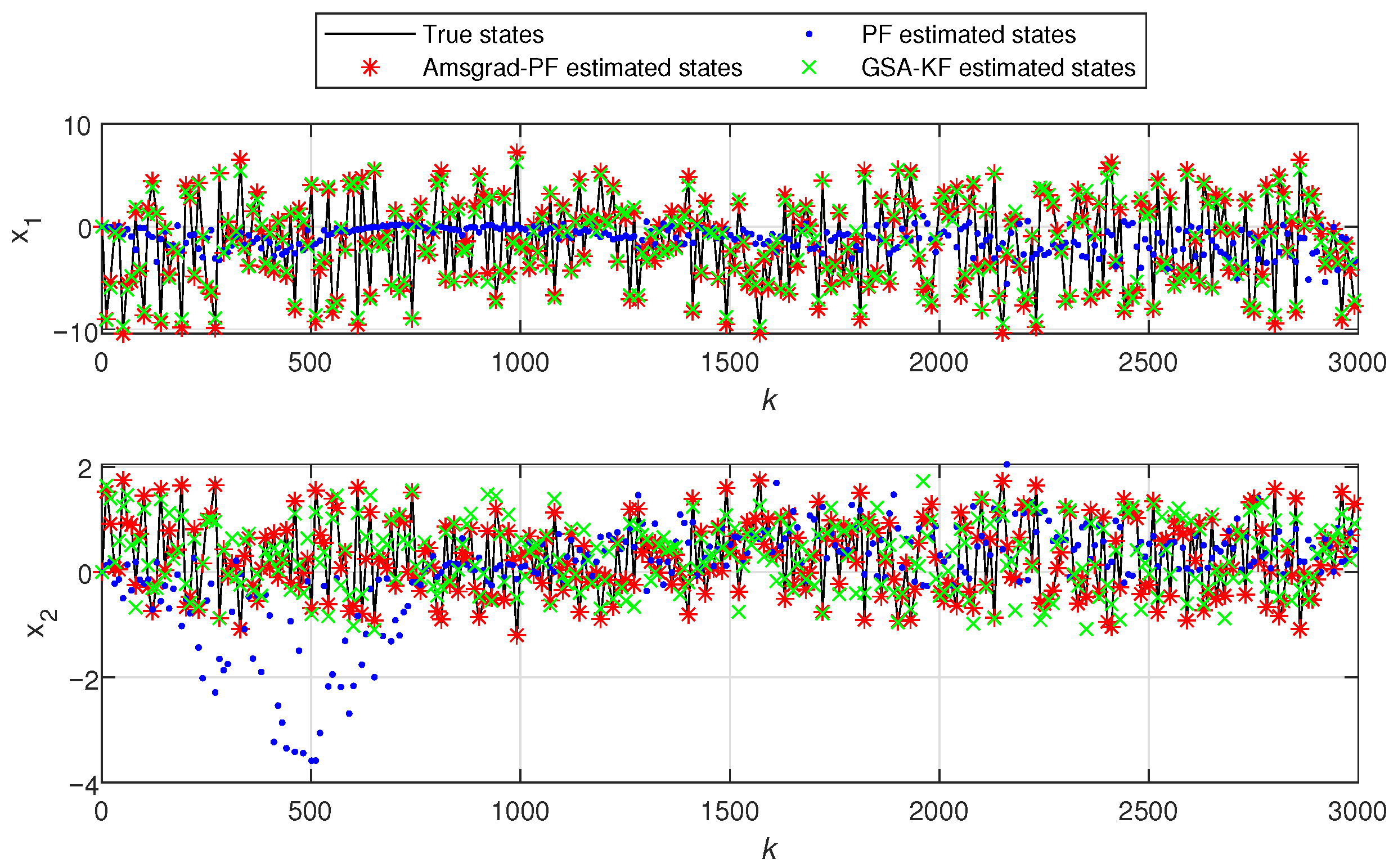
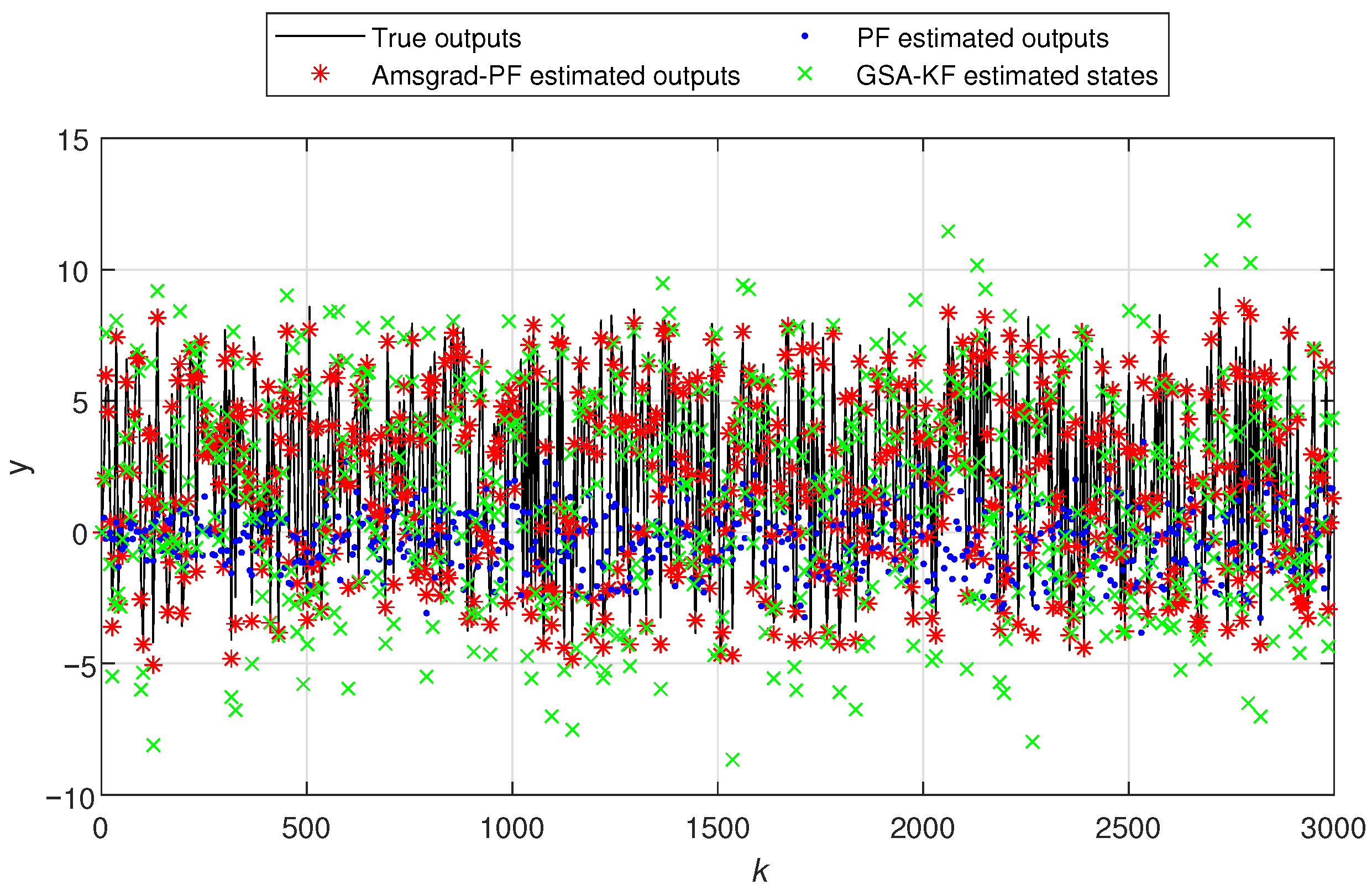
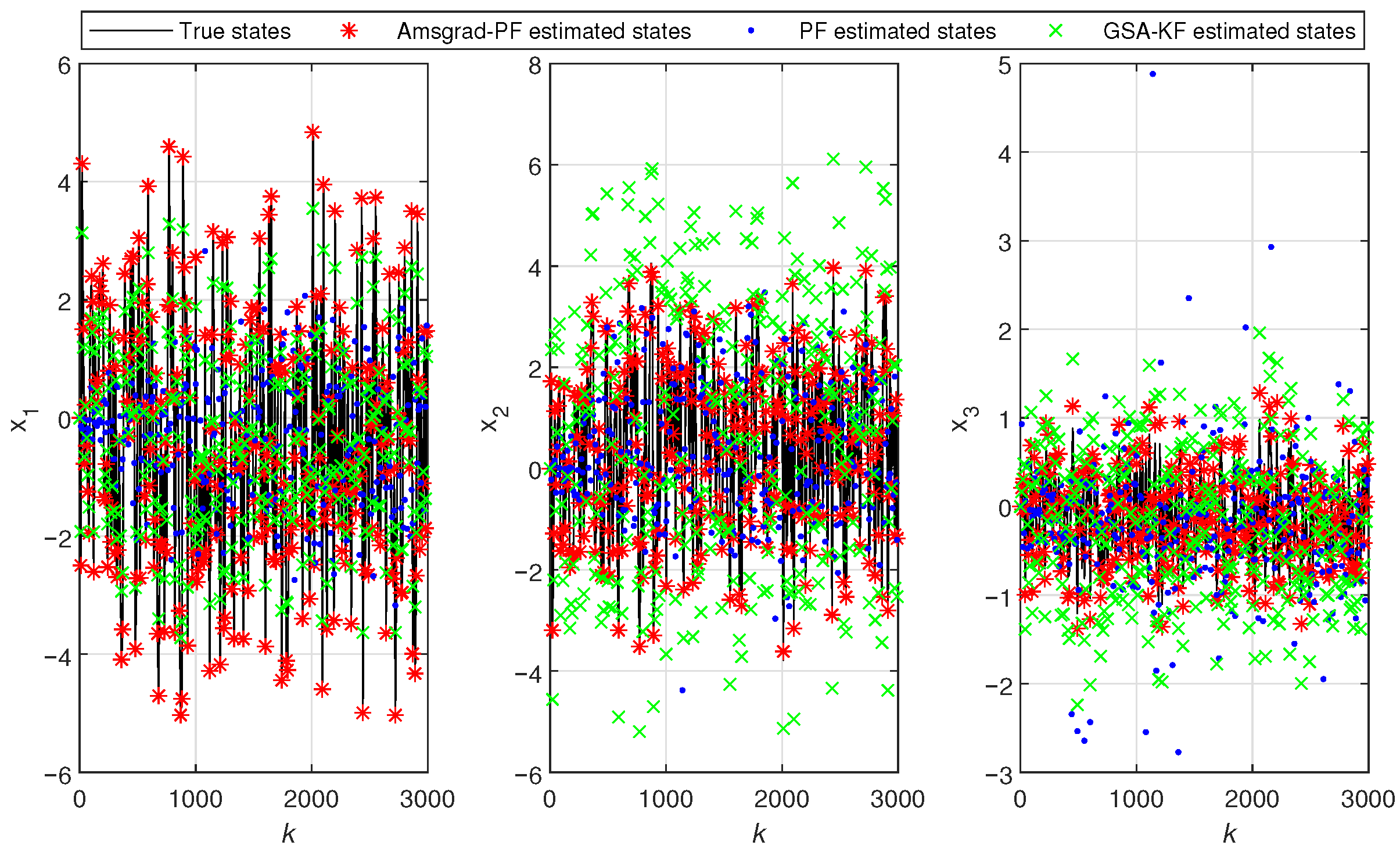
- In Figure 5 and Figure 10, the black line represents the true output, the red stars indicate the estimated outputs of Ams-PF, the blue dots represent the estimated outputs of PF, and the green forks denote the estimated outputs of GSA-KF. The system states in Figure 6 and Figure 11 are the same. As can be seen from these figures, the red stars are closest to the black line, which means that the estimated outputs and states of Ams-PF have a best fit with the true output and state values. These performances further demonstrate that the Ams-PF algorithm achieves satisfactory fitting between estimated and actual states, estimated outputs and actual outputs. The fitting performance is excellent and clearly superior to that of the PF and GSA-KF. Thus, the Ams-PF algorithm can effectively accomplish state estimation for fractional singular systems.
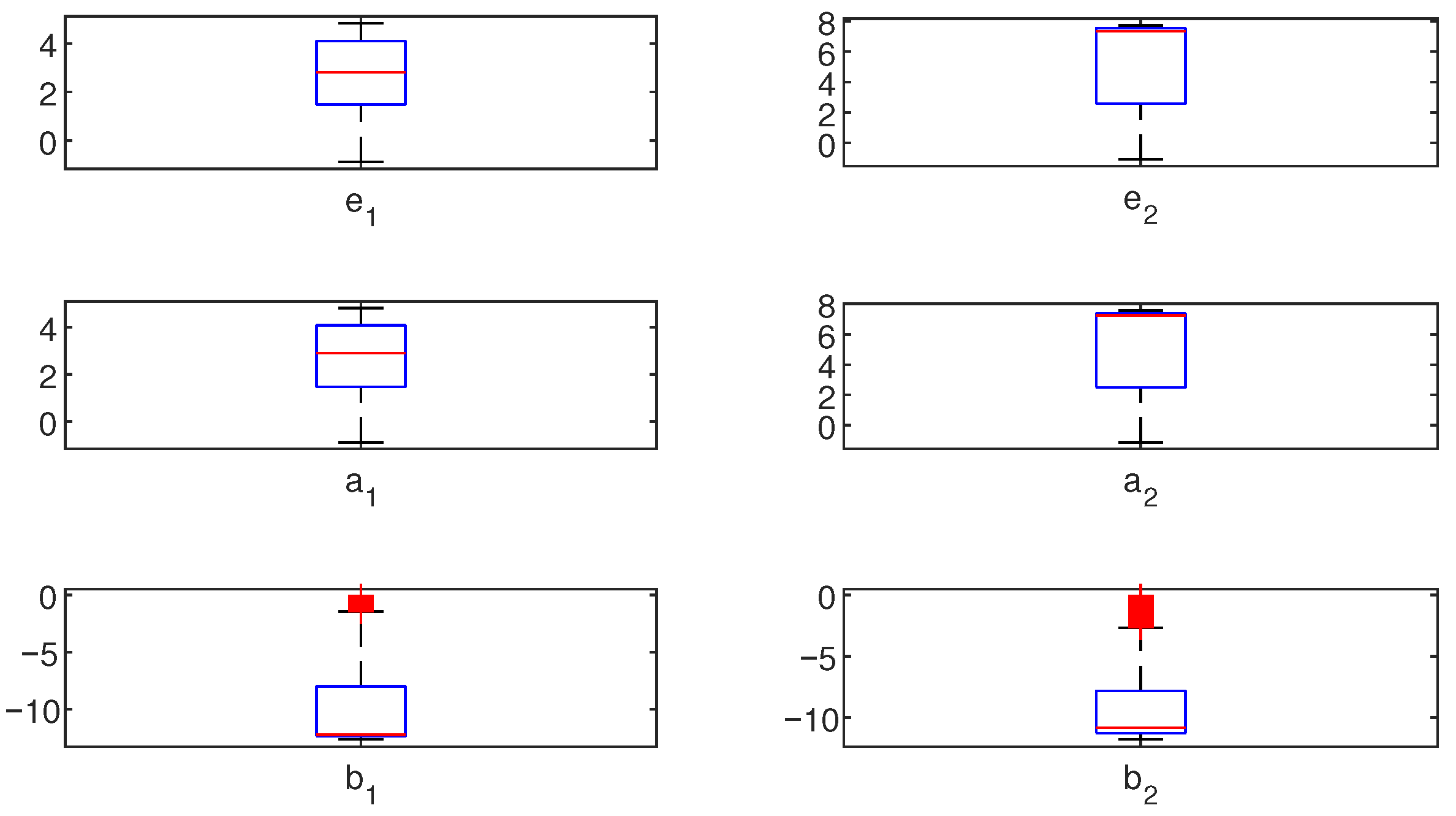
- From Table 2 and Figure 7, it can be seen that as the noise variance increases, the parameter estimation error becomes larger. However, this change is very minor. In Table 4, the final average value of Ams-PF identification error is 1.15654 and the standard deviation is 0.30091. Thus, we can conclude that the Ams-PF method can guarantee a certain robustness under different noise interferences or parameter uncertainty.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PF | Particle Filter |
| Ams-PF | Amsgrad-Particle Filter |
| Adam | Adaptive Moment Estimation |
| GL | Grünwald–Letnikov |
| GSA-KF | Gravitational Search Algorithm-Kalman Filter |
References
- Alsaedi, R. Existence results related to a singular fractional double-phase problem in the whole space. Fractal Fract. 2024, 8, 292. [Google Scholar] [CrossRef]
- Liu, X.; Yang, R. Predefined-time adaptive robust control of a class of nonlinear singular systems. Proc. Inst. Mech. Eng. Part J. Syst. Control Eng. 2024, 239, 3–15. [Google Scholar] [CrossRef]
- Li, H.; Zhou, B.; Michiels, W. Prescribed-time unknown input observers design for singular systems: A periodic delayed output approach. IEEE Trans. Syst. Man Cybern. Syst. 2023, 54, 741–751. [Google Scholar] [CrossRef]
- Hong, L.; Zhang, N. On the preconditioned MINRES method for solving singular linear systems. Comput. Appl. Math. 2022, 41, 1007–1026. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y. Global classical solutions of a nonlinear consumption system with singular density-suppressed motility. Appl. Math. Lett. 2024, 151, 1021–1034. [Google Scholar] [CrossRef]
- Zhang, Q.; Lu, J. H∞ control for singular fractional-order interval systems. ISA Trans. 2021, 110, 105–106. [Google Scholar] [CrossRef] [PubMed]
- Shu, Y.; Li, B.; Zhu, Y. Optimal control for uncertain discrete-time singular systems under expected value criterion. Fuzzy Optim. Decis. Mak. 2020, 20, 331–364. [Google Scholar] [CrossRef]
- Liu, R.; Chang, X.; Chen, Z. Dissipative control for switched nonlinear singular systems with dynamic quantization. Commun. Nonlinear Sci. Numer. Simul. 2023, 127, 102–108. [Google Scholar] [CrossRef]
- Zhang, Y.; Mu, X. Event-triggered output quantized control of discrete Markovian singular systems. Automatica 2022, 135, 109–110. [Google Scholar] [CrossRef]
- Allahverdiev, B.; Tuna, H. Singular discontinuous Hamiltonian systems. J. Appl. Anal. Comput. 2022, 12, 1386–1402. [Google Scholar] [CrossRef] [PubMed]
- Ristic, B.; Houssineau, J. Robust target motion analysis using the possibility particle filter. IET Radar Sonar Navig. 2019, 13, 18–22. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, Q.; Wei, Y. State of charge estimation by square root cubature particle filter approach with fractional order model of lithium-ion battery. Sci. China-Technol. Sci. 2022, 65, 1760–1771. [Google Scholar] [CrossRef]
- Xie, X.; Du, J.; Wu, J. Adaptive particle filter for change point detection of profile data in manufacturing systems. IEEE Trans. Autom. Sci. Eng. 2024, 21, 7143–7157. [Google Scholar] [CrossRef]
- Michalski, J.; Kozierski, P. MultiPDF particle filtering in state estimation of nonlinear objects. Nonlinear Dyn. 2021, 106, 2165–2182. [Google Scholar] [CrossRef]
- Abolmasoumi, A.; Farahani, A.; Mili, L. Robust particle filter design with an application to power system state estimation. IEEE Trans. Power Syst. 2024, 39, 1810–1821. [Google Scholar] [CrossRef]
- Bao, F.; Cao, Y.; Han, X. An implicit algorithm of solving nonlinear filtering problems. Commun. Comput. Phys. 2014, 16, 382–402. [Google Scholar] [CrossRef]
- Kang, J.; Chen, X.; Tao, Y. Optimal transportation particle filter for linear filtering systems with correlated noises. IEEE Trans. Aerosp. Electron. Syst. 2023, 58, 5190–5203. [Google Scholar] [CrossRef]
- Waseem; Ullah, A.; Awwad, F.; Ismail, E. Analysis of the corneal geometry of the human eye with an artificial neural network. Fractal Fract. 2023, 7, 764. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z. Data-driven product design evaluation method based on multi-stage artificial neural network. Appl. Soft Comput. 2021, 103, 1302–1317. [Google Scholar] [CrossRef]
- Chang, Z.; Zhang, Y.; Chen, W. Electricity price prediction based on hybrid model of adam optimized LSTM neural network and wavelet transform. Energy 2019, 187, 1000–1016. [Google Scholar] [CrossRef]
- Chen, H.; Shi, Y.; Zhang, J.; Zhao, Y. Sharp error estimate of a Grünwald–Letnikov scheme for reaction-subdiffusion equations. Numer. Algorithms 2022, 89, 1465–1477. [Google Scholar] [CrossRef]
- Zong, T.; Li, J.; Lu, G. Identification of fractional order Wiener-Hammerstein systems based on adaptively fuzzy PSO and data filtering technique. Appl. Intell. 2022, 52, 1–14. [Google Scholar] [CrossRef]
- Zhang, Q.; Lu, J. Novel admissibility and robust stabilization conditions for fractional-order singular systems with polytopic uncertainties. Asian J. Control 2024, 26, 70–84. [Google Scholar] [CrossRef]
- Tong, Q.; Liang, G.; Bi, J. Calibrating the adaptive learning rate to improve convergence of ADAM. Neurocomputing 2022, 481, 333–356. [Google Scholar] [CrossRef] [PubMed]
- Aspeel, A.; Gouverneur, A.; Jungers, R. Optimal intermittent particle filter. IEEE Trans. Signal Process. 2022, 70, 2814–2825. [Google Scholar] [CrossRef]
- Zong, T.; Li, J.; Lu, G. Maximum likelihood LM identification based on particle filtering for scarce measurement-data MIMO Hammerstein Box-Jenkins systems. Math. Comput. Simul. 2025, 230, 241–255. [Google Scholar] [CrossRef]
- Habibi, Z.; Zayyani, H.; Korki, M. A robust Markovian block sparse adaptive algorithm with its convergence analysis. IEEE Trans. Circuits Syst. Ii Express Briefs 2024, 71, 1546–1550. [Google Scholar] [CrossRef]
- Padhy, M.; Vigneshwari, S.; Ratnam, M. Application of empirical Bayes adaptive estimation technique for estimating winds from MST radar covering higher altitudes. Signal Image Video Process. 2023, 17, 3303–3311. [Google Scholar] [CrossRef]
- Li, J.; Xiao, K.; Gu, J.; Hua, L. Parameter estimation of multiple-input single-output Hammerstein controlled autoregressive system based on improved adaptive moment estimation algorithm. Int. J. Robust Nonlinear Control 2023, 33, 7094–7113. [Google Scholar] [CrossRef]
- Yang, M.; Yue, F.; Lu, B.; Zhao, H.; Ma, G.; Wang, L. Quantum gate control pulse optimization based on the Adam algorithm. Quantum Inf. Process. 2025, 24, 175. [Google Scholar] [CrossRef]
- Iqbal, N.; Wang, H.; Zheng, Z.; Yao, M. Reinforcement learning-based heuristic planning for optimized energy management in power-split hybrid electric heavy duty vehicles. Energy 2024, 302, 131773. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Y.; Yan, Y. Parallel and distributed asynchronous adaptive stochastic gradient methods. Math. Program. Comput. 2023, 15, 471–508. [Google Scholar] [CrossRef]
- Radhakrishnan, P.; Senthilkumar, G. Nesterov-accelerated adaptive moment estimation NADAM-LSTM based text summarization. J. Intell. Fuzzy Syst. 2024, 46, 6781–6793. [Google Scholar]
- Li, X.; Yin, Y.; Feng, R. Double total variation (DTV) regularization and improved adaptive moment estimation (IADAM) optimization method for fast MR image reconstruction. Comput. Methods Programs Biomed. 2023, 233, 6172–6201. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Liu, X.; Ji, K.; Lei, Y. Convergence of adaptive stochastic mirror descent. IEEE Trans. Neural Netw. Learn. Syst. 2025, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Crisan, D.; Doucet, A. A survey of convergence results on particle filtering methods for practitioners. IEEE Trans. Signal Process. 2002, 50, 736–746. [Google Scholar] [CrossRef]
- Hu, X.; Schön, T.; Ljung, L. A general convergence result for particle filtering. IEEE Trans. Signal Process. 2011, 59, 3424–3429. [Google Scholar] [CrossRef]

| Algorithm | Parameter | k = 100 | k = 200 | k = 500 | k = 1000 | k = 2000 | k = 3000 | True Value |
|---|---|---|---|---|---|---|---|---|
| Ams-PF | −0.61541 | −0.02476 | 1.14192 | 4.72356 | 3.35476 | 1.35720 | 1.45000 | |
| −1.06909 | −0.92999 | −0.24511 | 6.48938 | 7.48246 | 7.68150 | 7.62000 | ||
| −0.62677 | −0.01994 | 1.18192 | 4.73852 | 3.42233 | 1.23715 | 1.29000 | ||
| −1.12186 | −0.97711 | −0.28772 | 6.38395 | 7.35942 | 7.56279 | 7.50000 | ||
| −4.49469 | −5.55102 | −6.21625 | −11.97485 | −12.32042 | −12.28608 | −12.23000 | ||
| −4.56647 | −5.58235 | −6.20746 | −11.42739 | −11.01381 | −10.81964 | −10.85000 | ||
| 81.67777 | 75.76372 | 68.40623 | 25.73892 | 14.63015 | 0.77586 | 0.00000 | ||
| Amsgrad | −0.00006 | −0.00006 | −0.00007 | −0.00007 | −0.00008 | −0.00009 | 1.45000 | |
| −0.00006 | −0.00006 | −0.00007 | −0.00007 | −0.00008 | −0.00009 | 7.62000 | ||
| −0.00006 | −0.00006 | −0.00007 | −0.00007 | −0.00008 | −0.00009 | 1.29000 | ||
| −0.00006 | −0.00006 | −0.00007 | −0.00007 | −0.00008 | −0.00009 | 7.50000 | ||
| −0.32544 | −0.58082 | −2.51044 | −5.70348 | −10.32070 | −13.04685 | −12.23000 | ||
| −0.40543 | −0.70195 | −3.22139 | −7.46451 | −11.53878 | −10.95777 | −10.85000 | ||
| 97.83775 | 96.21691 | 83.81867 | 66.83424 | 56.31184 | 55.51342 | 0.00000 | ||
| GSA-KF | 1.60228 | 1.87892 | 2.13652 | 0.55312 | 1.70922 | 0.71478 | 1.45000 | |
| 1.11366 | 0.46282 | 2.17060 | 1.04038 | 2.37803 | 2.59275 | 7.62000 | ||
| 0.43591 | −0.22426 | 0.78218 | −0.10266 | 0.24588 | −0.31317 | 1.29000 | ||
| 0.99366 | 0.74029 | −0.33393 | 0.82055 | −0.26198 | 0.97589 | 7.50000 | ||
| −5.61093 | −6.65074 | −11.22424 | −13.54027 | −13.27158 | −12.65576 | −12.23000 | ||
| −3.68962 | −4.99514 | −9.76241 | −8.89775 | −10.09497 | −8.62924 | −10.85000 | ||
| 68.43794 | 56.61571 | 45.42038 | 44.01233 | 40.03237 | 40.03237 | 0.00000 |
| Noise | k | |||||||
|---|---|---|---|---|---|---|---|---|
| 100 | −0.61993 | −1.07816 | −0.63087 | −1.12662 | −4.51960 | −4.59531 | 81.58529 | |
| 200 | −0.02616 | −0.93060 | −0.02162 | −0.97967 | −5.58548 | −5.62083 | 75.62647 | |
| 500 | 1.12818 | −0.25172 | 1.16804 | −0.29629 | −6.24719 | −6.24261 | 68.32139 | |
| 1000 | 4.68612 | 6.42875 | 4.69650 | 6.32621 | −11.92001 | −11.38289 | 25.59878 | |
| 2000 | 3.26999 | 7.44564 | 3.35706 | 7.30810 | −12.31156 | −11.00405 | 14.11934 | |
| 3000 | 1.56226 | 7.55420 | 1.38692 | 7.44336 | −12.32993 | −10.86013 | 1.01396 | |
| 100 | −0.62497 | −1.07610 | −0.63717 | −1.13089 | −4.57133 | −4.65109 | 81.37875 | |
| 200 | −0.03067 | −0.93304 | −0.02977 | −0.98243 | −5.64181 | −5.68185 | 75.41060 | |
| 500 | 1.10890 | −0.26537 | 1.14559 | −0.31072 | −6.29412 | −6.29484 | 68.21139 | |
| 1000 | 4.61111 | 6.31260 | 4.61662 | 6.21463 | −11.79260 | −11.27850 | 25.36458 | |
| 2000 | 3.24096 | 7.30739 | 3.32794 | 7.16698 | −12.27024 | −10.98292 | 14.03265 | |
| 3000 | 1.63235 | 7.34108 | 1.42873 | 7.24212 | −12.31576 | −10.87492 | 2.30512 | |
| True Value | 1.45000 | 7.62000 | 1.29000 | 7.50000 | −12.23000 | −10.85000 | 0.00000 | |
| Algorithm | Parameter | k = 100 | k = 200 | k = 500 | k = 1000 | k = 2000 | k = 3000 | True Value |
|---|---|---|---|---|---|---|---|---|
| Ams-PF | −4.15262 | −5.26322 | −5.93478 | −5.67812 | −5.17051 | −4.28444 | −4.35000 | |
| −3.89106 | −4.56233 | −4.68299 | −4.80976 | −5.13349 | −5.62614 | −5.60000 | ||
| −3.37188 | −3.87983 | −4.22355 | −4.13936 | −3.58811 | −3.22194 | −3.22000 | ||
| −4.02288 | −5.03670 | −5.81737 | −5.54977 | −5.08730 | −4.22023 | −4.30000 | ||
| −3.91768 | −4.78959 | −4.76688 | −4.92696 | −5.06612 | −5.55220 | −5.55000 | ||
| −3.42535 | −3.75496 | −4.09824 | −3.97158 | −3.57478 | −3.16901 | −3.17000 | ||
| −2.37429 | −1.65605 | 0.06044 | 0.18526 | −0.13507 | −0.31770 | −0.38000 | ||
| −1.52845 | 0.18578 | 4.08040 | 5.78942 | 6.28496 | 6.49679 | 6.50000 | ||
| −1.30907 | −0.48574 | 1.46846 | 1.76074 | 1.57158 | 1.36158 | 1.33000 | ||
| 70.32583 | 54.41356 | 29.41611 | 20.40704 | 11.59974 | 0.99473 | 0.00000 | ||
| Amsgrad | −2.00252 | −2.08265 | −2.09940 | −2.09940 | −2.09940 | −2.09941 | −4.35000 | |
| −2.00252 | −2.08265 | −2.09940 | −2.09940 | −2.09940 | −2.09941 | −5.60000 | ||
| −2.00252 | −2.08265 | −2.09940 | −2.09940 | −2.09940 | −2.09941 | −3.22000 | ||
| −2.00252 | −2.08265 | −2.09940 | −2.09940 | −2.09940 | −2.09941 | −4.30000 | ||
| −2.00252 | −2.08265 | −2.09940 | −2.09940 | −2.09940 | −2.09941 | −5.55000 | ||
| −2.00252 | −2.08265 | −2.09940 | −2.09940 | −2.09940 | −2.09941 | −3.17000 | ||
| 2.40826 | −0.55162 | −0.33212 | −0.45776 | 1.02542 | −1.80296 | −0.38000 | ||
| 8.37223 | 6.67781 | 6.45143 | 6.78119 | 8.72513 | 5.86281 | 6.50000 | ||
| 3.13573 | 0.18506 | 0.42633 | 0.29708 | 1.43440 | −0.39791 | 1.33000 | ||
| 64.55746 | 61.10604 | 61.10887 | 61.24270 | 62.02571 | 61.68410 | 0.00000 | ||
| GSA-KF | 0.82003 | 1.00473 | 2.03327 | −2.68556 | −3.48806 | −3.42608 | −4.35000 | |
| 1.67698 | 1.20865 | 0.93494 | 2.64296 | 1.08677 | −2.40842 | −5.60000 | ||
| 0.46681 | 0.01001 | −0.43139 | −1.08602 | 1.30994 | −2.98696 | −3.22000 | ||
| 0.75629 | −0.19207 | −0.36270 | 0.99605 | −0.31427 | −1.31883 | −4.30000 | ||
| 0.49804 | −0.54719 | −0.10848 | −0.79584 | −0.28896 | −1.59978 | −5.55000 | ||
| −0.25889 | −0.73610 | −0.09367 | −0.08238 | 0.51672 | −1.45601 | −3.17000 | ||
| 0.49905 | −0.41279 | −0.91987 | −0.02331 | −0.96026 | −0.36071 | −0.38000 | ||
| 4.54039 | 5.34174 | 5.50382 | 6.17914 | 6.01744 | 6.21313 | 6.50000 | ||
| 0.84229 | 0.78674 | 0.43152 | 2.44888 | 2.52241 | 0.42249 | 1.33000 | ||
| 95.02548 | 88.95787 | 86.56646 | 85.57912 | 63.56020 | 46.87218 | 0.00000 |
| k | |||||
|---|---|---|---|---|---|
| 100 | |||||
| 200 | |||||
| 500 | |||||
| 1000 | |||||
| 2000 | |||||
| 3000 | |||||
| k | |||||
| 100 | |||||
| 200 | |||||
| 500 | |||||
| 1000 | |||||
| 2000 | |||||
| 3000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Zhao, K.; Wang, Z.; Zong, T. Joint Parameter and State Estimation of Fractional-Order Singular Systems Based on Amsgrad and Particle Filter. Fractal Fract. 2025, 9, 480. https://doi.org/10.3390/fractalfract9080480
Sun T, Zhao K, Wang Z, Zong T. Joint Parameter and State Estimation of Fractional-Order Singular Systems Based on Amsgrad and Particle Filter. Fractal and Fractional. 2025; 9(8):480. https://doi.org/10.3390/fractalfract9080480
Chicago/Turabian StyleSun, Tianhang, Kaiyang Zhao, Zhen Wang, and Tiancheng Zong. 2025. "Joint Parameter and State Estimation of Fractional-Order Singular Systems Based on Amsgrad and Particle Filter" Fractal and Fractional 9, no. 8: 480. https://doi.org/10.3390/fractalfract9080480
APA StyleSun, T., Zhao, K., Wang, Z., & Zong, T. (2025). Joint Parameter and State Estimation of Fractional-Order Singular Systems Based on Amsgrad and Particle Filter. Fractal and Fractional, 9(8), 480. https://doi.org/10.3390/fractalfract9080480






