Analytical Description of Three-Dimensional Fractal Surface Wear Process Based on Multi-Stage Contact Theory
Abstract
1. Introduction
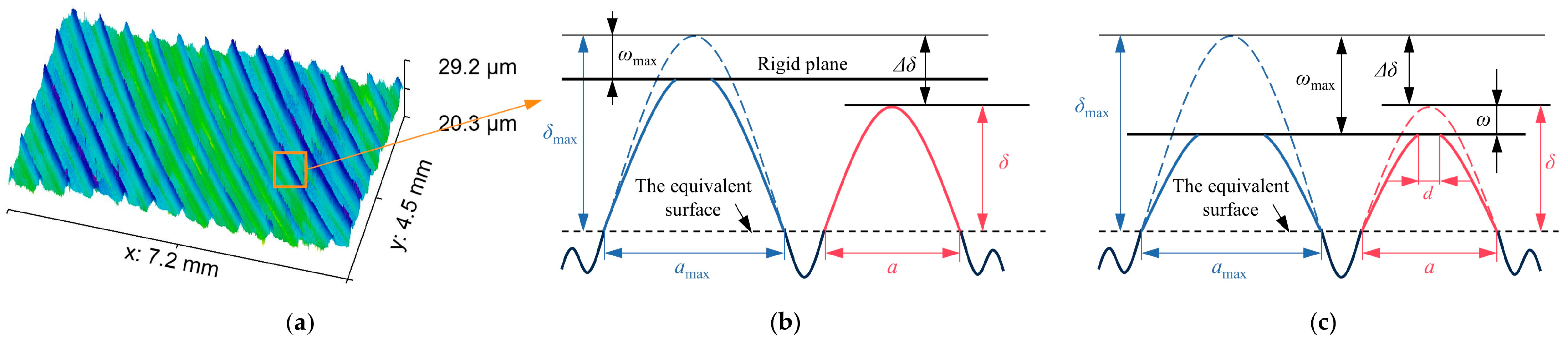
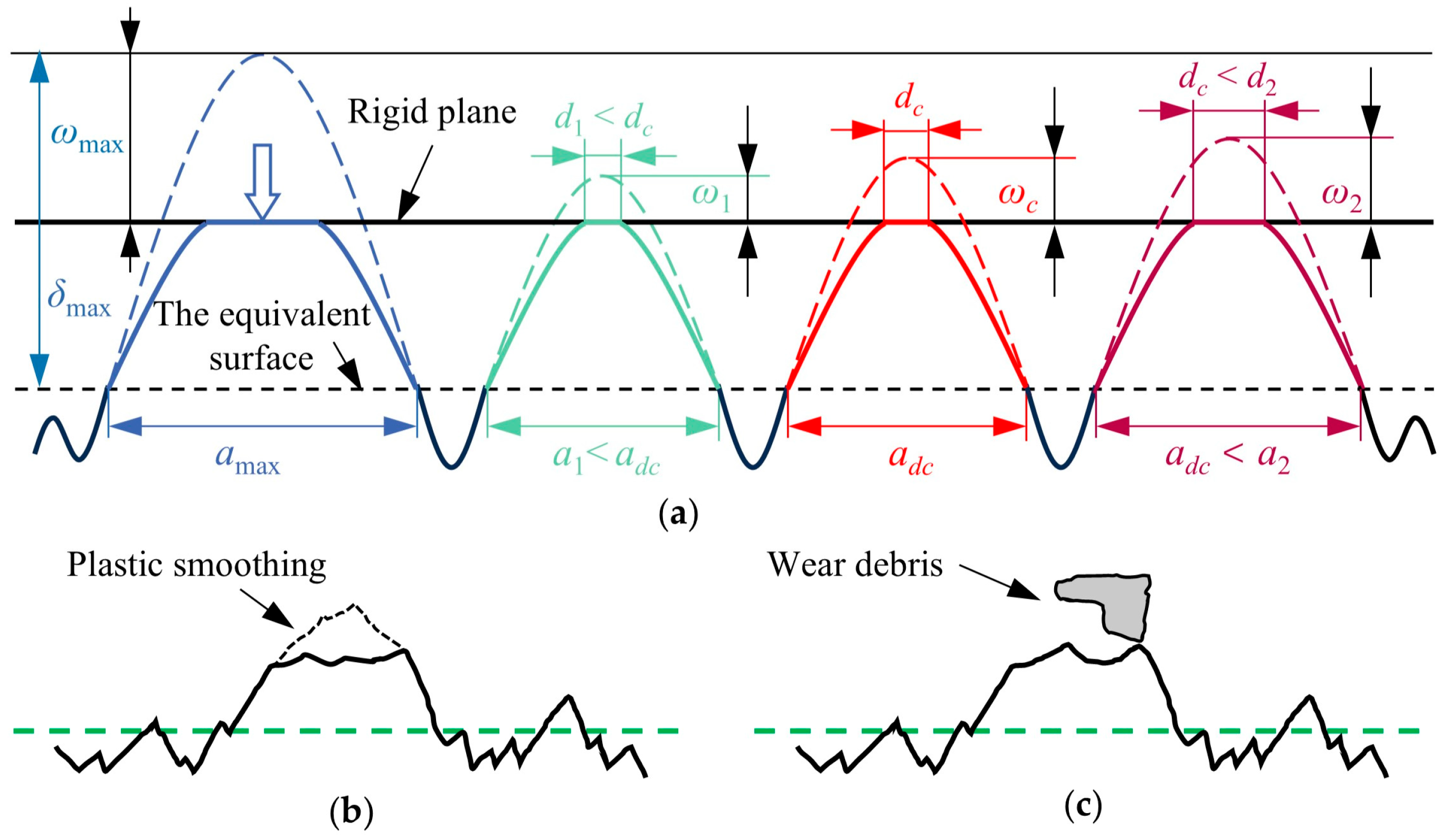
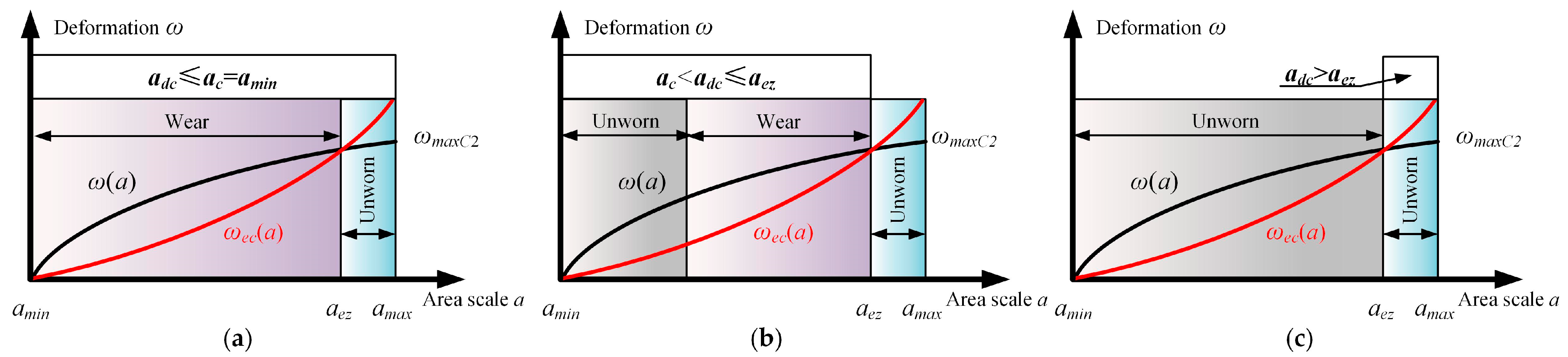
2. Critical Area Scale Model for Controlling the Formation of Abrasive Particles
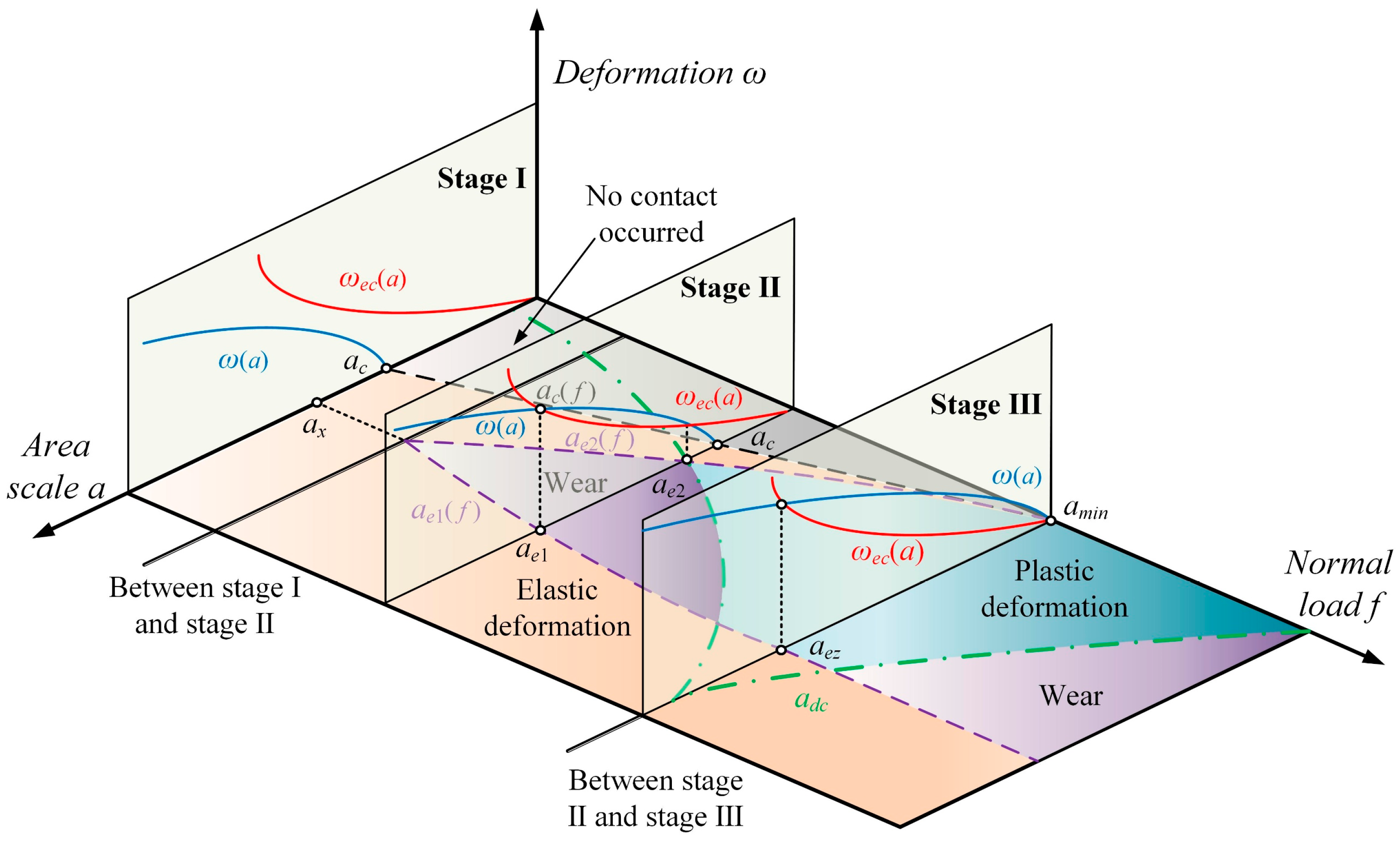
3. Wear Coefficient Modeling of Multiple Asperities Based on Multi-Stage Contact Theory
3.1. A Brief Description of the Wear Coefficient
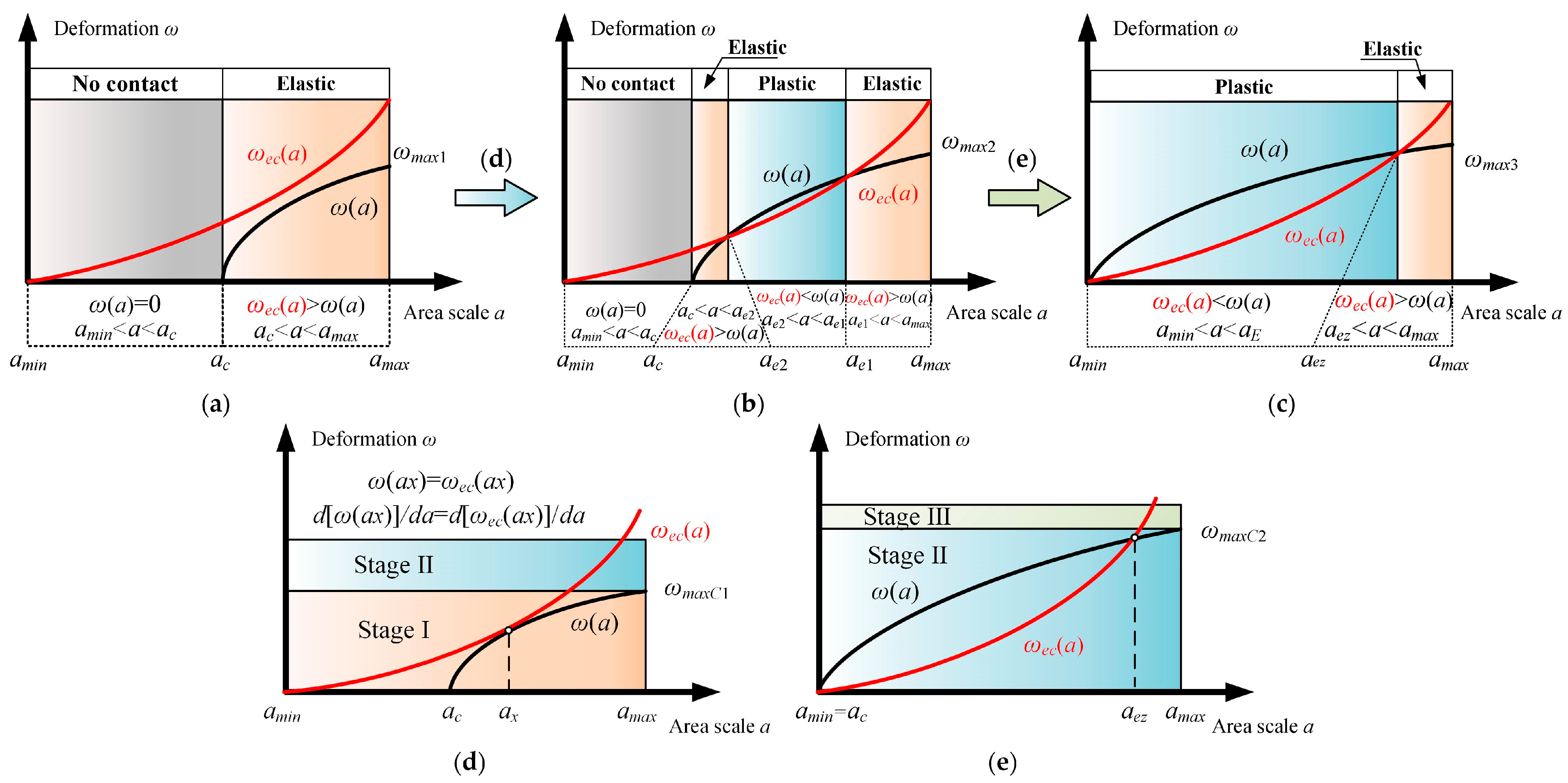
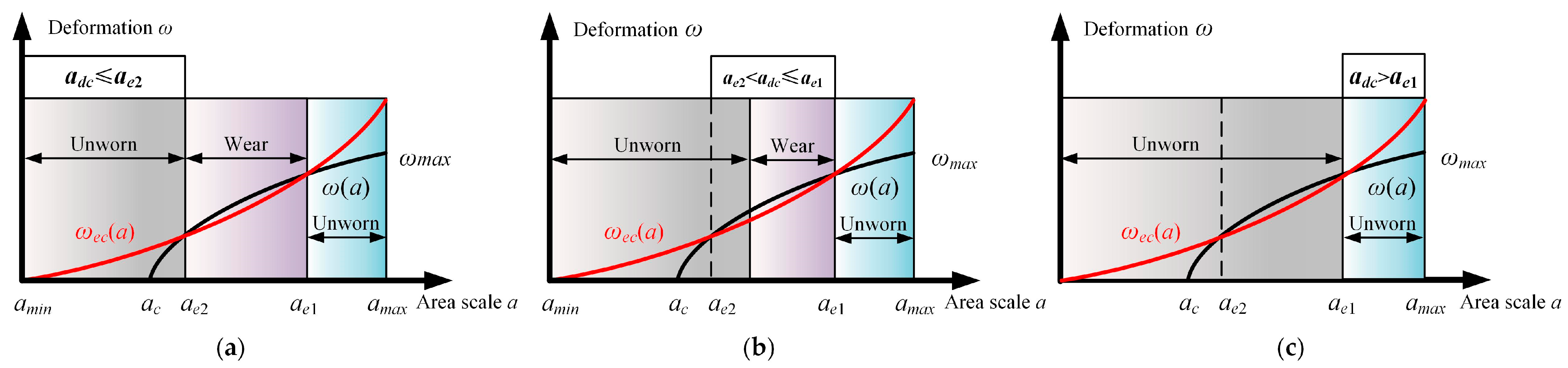
3.2. Wear Coefficient Modeling Based on the Multi-Stage Contact Theory
4. Establishment of Three-Dimensional Surface Wear Mathematical Model
5. Results and Discussion
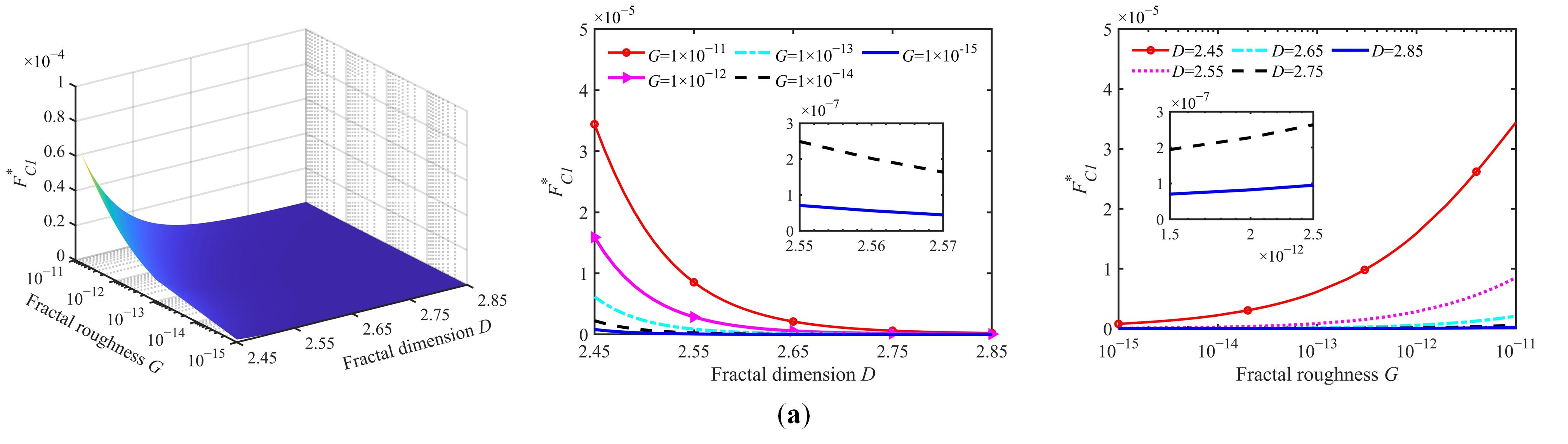
5.1. The Variation of the Critical Load
5.2. The Relationship Between Wear Rate and Normal Contact Load

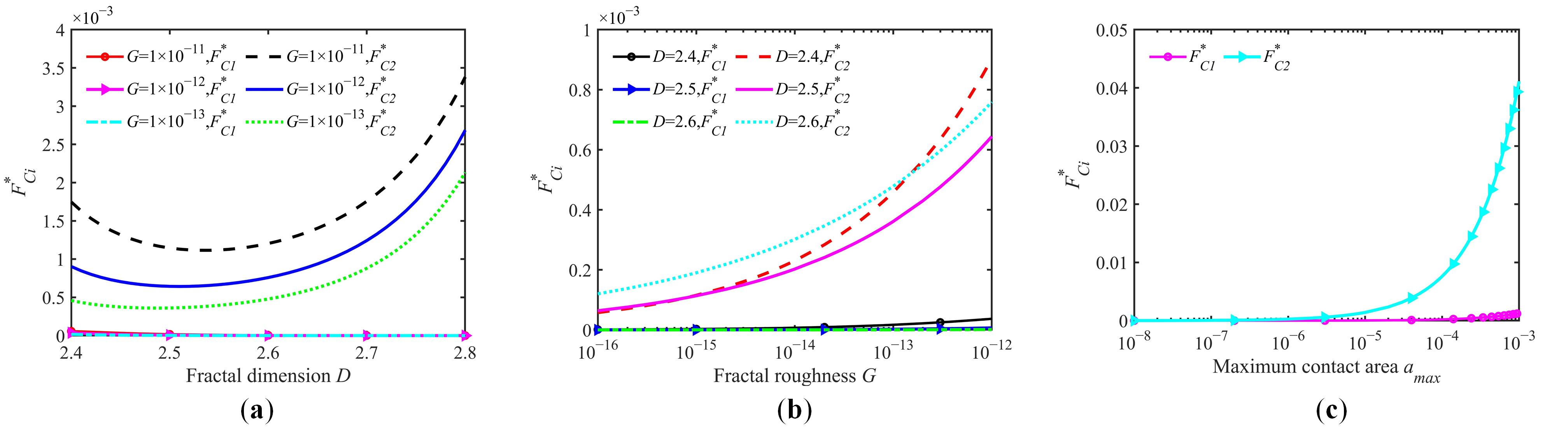
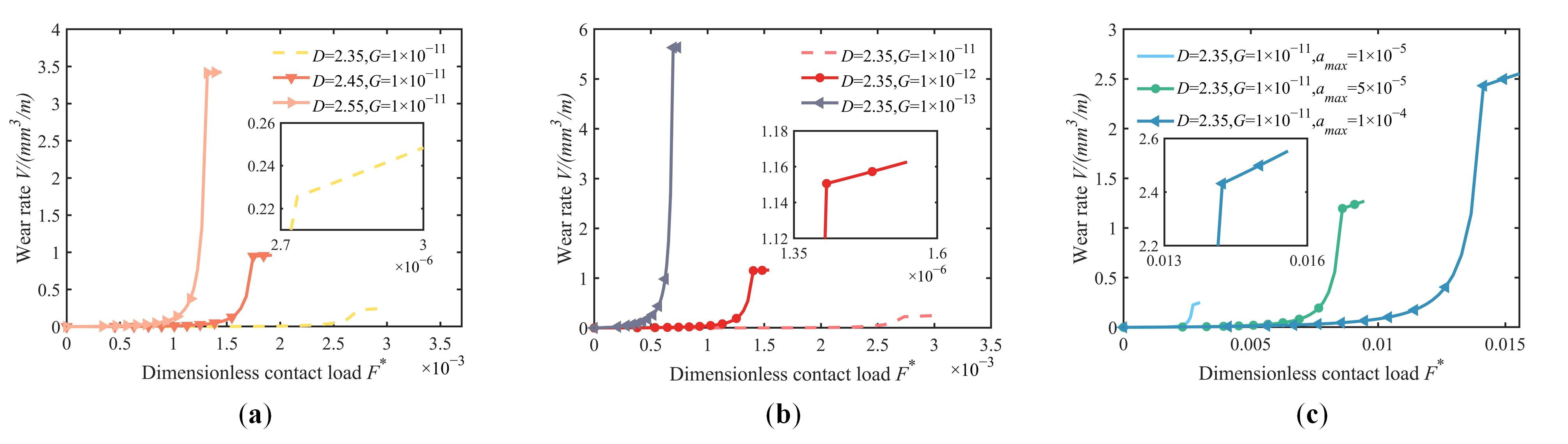
5.3. The Effect of Different Surface Parameters on the Volume Wear Rate
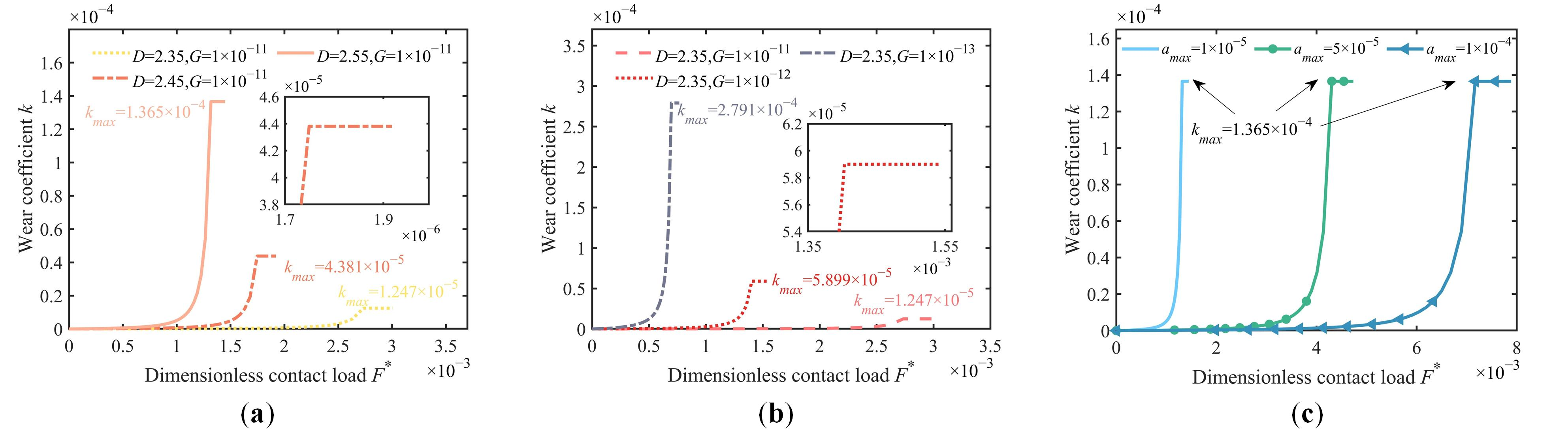
5.4. The Influence of Different Surface Parameters on the Wear Coefficient
6. Experimental Verifications
6.1. The Experimental Process
| Factors | Turning Surfaces | Grinding Surfaces | Milling Surfaces | Cylindrical Pins |
|---|---|---|---|---|
| Material properties | Q235 steel | 304 stainless steel | ||
| Fractal dimension (D) | 2.420 | 2.347 | 2.384 | - |
| Fractal roughness (G) | 1.032 × 10−11 m | 1.210 × 10−11 m | 1.532 × 10−11 m | - |
| Young’s modulus | 210 GPa | 193 GPa | ||
| Hardness | 155 HB | 200 HB | ||
| Poisson ratio | 0.27 | 0.3 | ||
| Number of specimens | 15 | 50 | ||
| Radius of the specimen | R1 = 1.25 cm | H1 = 0.3 mm | ||
| Height of the specimen | R2 = 0.5 cm | H2 = 8 mm | ||
6.2. Comparison of Simulation and Test Results
7. Conclusions
- (1)
- The volumetric wear rate exhibits nonlinear variation with the contact load under specific operating conditions. It becomes more linear when the contact load is higher, and the transition in wear stages aligns with changes in wear rate stages.
- (2)
- Surface parameters exhibit distinct impacts on the critical contact load and wear coefficient. Higher surface roughness makes it easier for the surface to enter stage II. Elevated fractal dimension D coupled with reduced fractal roughness G correspond to increased maximum wear coefficient values. In contrast, variations in the maximum asperity contact area amax demonstrate negligible influence on wear coefficient magnitude.
- (3)
- The comparison between pin-on-disc wear test results and model predictions reveals that the maximum relative errors for turning, grinding, and milling surfaces are 18.42%, 18.76%, and 23.92% respectively, all confined within 25%. Compared with existing models, the wear rate prediction model developed in this study based on multi-stage contact theory for three-dimensional surfaces demonstrates higher prediction accuracy. These findings simultaneously validate the existence of the three-dimensional surface multi-stage wear phenomenon proposed previously, establishing a theoretical foundation for mechanistically understanding three-dimensional surface multi-stage wear.
- (4)
- The surface wear model established in this study focuses primarily on the initial wear stage under non-severe deformation conditions. Its accuracy may decrease under high-speed and high-load operating conditions. In addition, this study does not fully consider the influence of complex processes, such as the retention of wear debris, on the actual friction and wear behavior, which can be further discussed in the future.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Burwell, J.T.; Strang, C.D. On the empirical law of adhesive wear. J. Appl. Phys. 1952, 23, 18–28. [Google Scholar] [CrossRef]
- Mishra, T.; De Rooij, M.; Schipper, D.J. The effect of asperity geometry on the wear behaviour in sliding of an elliptical asperity. Wear 2021, 470–471, 203615. [Google Scholar] [CrossRef]
- Shen, F.; Li, Y.H.; Ke, L.L. A novel fractal contact model based on size distribution law. Int. J. Mech. Sci. 2023, 249, 108255. [Google Scholar] [CrossRef]
- Li, Y.H.; Shen, F.; Güler, M.A.; Ke, L.L. An efficient method for electro-thermo-mechanical coupling effect in electrical contact on rough surfaces. Int. J. Heat Mass Transf. 2024, 226, 125492. [Google Scholar] [CrossRef]
- Pitenis, A.A.; Dowson, D.; Gregory Sawyer, W. Leonardo da vinci’s friction experiments: An old story acknowledged and repeated. Tribol. Lett. 2014, 56, 509–515. [Google Scholar] [CrossRef]
- Zhang, H.; Goltsberg, R.; Etsion, I. Modeling adhesive wear in asperity and rough surface contacts: A review. Materials 2022, 15, 6855. [Google Scholar] [CrossRef] [PubMed]
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Liu, B.; Bruni, S.; Lewis, R. Numerical calculation of wear in rolling contact based on the archard equation: Effect of contact parameters and consideration of uncertainties. Wear 2022, 490–491, 204188. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Liu, M.; Wu, S. Analytical description of the wear process using a multi-stage contact fractal approach. Wear 2024, 548–549, 205364. [Google Scholar] [CrossRef]
- Shirong, G.; Gouan, C. Fractal prediction models of sliding wear during the running-in process. Wear 1999, 231, 249–255. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, X.; Xu, J.; Jiang, H.; Li, N.; Si, J. A study on building and testing fractal model for predicting end face wear of aeroengine’s floating ring seal. Wear 2023, 532–533, 205079. [Google Scholar] [CrossRef]
- Hao, Q.; Yin, J.; Liu, Y.; Jin, L.; Zhang, S.; Sha, Z. Time-varying wear calculation method for fractal rough surfaces of friction pairs. Coatings 2023, 13, 270. [Google Scholar] [CrossRef]
- Schirmeisen, A. One atom after the other. Nat. Nanotechnol. 2013, 8, 81–82. [Google Scholar] [CrossRef] [PubMed]
- Chung, K.H. Wear characteristics of atomic force microscopy tips: A review. Int. J. Precis. Eng. Manuf. 2014, 15, 2219–2230. [Google Scholar] [CrossRef]
- Rabinowicz, E. The effect of size on the looseness of wear fragments. Wear 1958, 2, 4–8. [Google Scholar] [CrossRef]
- Aghababaei, R.; Warner, D.H.; Molinari, J.F. Critical length scale controls adhesive wear mechanisms. Nat. Commun. 2016, 7, 11816. [Google Scholar] [CrossRef] [PubMed]
- Frérot, L.; Aghababaei, R.; Molinari, J.F. A mechanistic understanding of the wear coefficient: From single to multiple asperities contact. J. Mech. Phys. Solids 2018, 114, 172–184. [Google Scholar] [CrossRef]
- Popov, V.L.; Pohrt, R. Adhesive wear and particle emission: Numerical approach based on asperity-free formulation of rabinowicz criterion. Friction 2018, 6, 260–273. [Google Scholar] [CrossRef]
- Popov, V.L.; Li, Q.; Lyashenko, I.A. Contact mechanics and friction: Role of adhesion. Friction 2025, 13, 9440964. [Google Scholar] [CrossRef]
- Dimaki, A.V.; Shilko, E.V.; Dudkin, I.V.; Psakhie, S.G.; Popov, V.L. Role of adhesion stress in controlling transition between plastic, grinding and breakaway regimes of adhesive wear. Sci. Rep. 2020, 10, 1585. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, T.D.B.; Gotsmann, B.; Lantz, M.A.; Carpick, R.W. On the application of transition state theory to atomic-scale wear. Tribol. Lett. 2010, 39, 257–271. [Google Scholar] [CrossRef]
- Gotsmann, B.; Lantz, M.A. Atomistic wear in a single asperity sliding contact. Phys. Rev. Lett. 2008, 101, 125501. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.B.; Li, L.; An, J. Dry wear behavior and mild-to-severe wear transition in an mg-gd-Y-zr alloy. Surf. Topogr. Metrol. Prop. 2021, 9, 25032. [Google Scholar] [CrossRef]
- Cho, S.J.; Moon, H.; Hockey, B.J.; Hsu, S.M. The transition from mild to severe wear in alumina during sliding. Acta Metall. Mater. 1992, 40, 185–192. [Google Scholar] [CrossRef]
- Hsu, S.M.; Shen, M. Wear prediction of ceramics. Wear 2004, 256, 867–878. [Google Scholar] [CrossRef]
- Ni, X.; Sun, J.; Ma, C.; Zhang, Y. Wear model of a mechanical seal based on piecewise fractal theory. Fractal Fract. 2023, 7, 251. [Google Scholar] [CrossRef]
- Zhang, J.; Alpas, A.T. Transition between mild and severe wear in aluminium alloys. Acta Mater. 1997, 45, 513–528. [Google Scholar] [CrossRef]
- Aghababaei, R.; Brink, T.; Molinari, J.F. Asperity-level origins of transition from mild to severe wear. Phys. Rev. Lett. 2018, 120, 186105. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liu, D.; Wang, C.; Zhang, W.; Zhu, L. A fractal contact model of rough surfaces considering detailed multi-scale effects. Tribol. Int. 2022, 176, 107920. [Google Scholar] [CrossRef]
- Zhou, W.; Cao, Y.; Zhao, H.; Li, Z.; Feng, P.; Feng, F. Fractal analysis on surface topography of thin films: A review. Fractal Fract. 2022, 6, 135. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, X.; Feng, F.; Feng, P.; Zhang, M. Calculation of fractal dimension based on artificial neural network and its application for machined surfaces. Fractals 2021, 29, 2150129. [Google Scholar] [CrossRef]
- Pan, W.; Li, X.; Wang, L.; Mu, J.; Yang, Z. A loading fractal prediction model developed for dry-friction rough joint surfaces considering elastic–plastic contact. Acta Mech. 2018, 229, 2149–2162. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Wu, S. Multi-stage contact model between fractal rough surfaces based on multi-scale asperity deformation. Appl. Math. Model. 2022, 109, 229–250. [Google Scholar] [CrossRef]
- Yan, W.; Komvopoulos, K. Contact analysis of elastic-plastic fractal surfaces. J. Appl. Phys. 1998, 84, 3617–3624. [Google Scholar] [CrossRef]
- Yin, X.; Komvopoulos, K. An adhesive wear model of fractal surfaces in normal contact. Int. J. Solids Struct. 2010, 47, 912–921. [Google Scholar] [CrossRef]
- Pan, W.; Sun, Y.; Li, X.; Song, H.; Guo, J. Contact mechanics modeling of fractal surface with complex multi-stage actual loading deformation. Appl. Math. Model. 2024, 128, 58–81. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Fractal model of elastic-plastic contact between rough surfaces. J. Tribol. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-plastic contact analysis of a sphere and a rigid flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Zhao, D.; Wu, S. A revised contact stiffness model of rough curved surfaces based on the length scale. Tribol. Int. 2021, 164, 107206. [Google Scholar] [CrossRef]
- Brink, T.; Frérot, L.; Molinari, J.F. A parameter-free mechanistic model of the adhesive wear process of rough surfaces in sliding contact. J. Mech. Phys. Solids 2021, 147, 104238. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Li, L.; Liu, Y.; Wang, J.; Li, Y.; Chen, G. Analytical Description of Three-Dimensional Fractal Surface Wear Process Based on Multi-Stage Contact Theory. Fractal Fract. 2025, 9, 463. https://doi.org/10.3390/fractalfract9070463
Zhang W, Li L, Liu Y, Wang J, Li Y, Chen G. Analytical Description of Three-Dimensional Fractal Surface Wear Process Based on Multi-Stage Contact Theory. Fractal and Fractional. 2025; 9(7):463. https://doi.org/10.3390/fractalfract9070463
Chicago/Turabian StyleZhang, Wang, Ling Li, Yang Liu, Jingjing Wang, Yao Li, and Guozhang Chen. 2025. "Analytical Description of Three-Dimensional Fractal Surface Wear Process Based on Multi-Stage Contact Theory" Fractal and Fractional 9, no. 7: 463. https://doi.org/10.3390/fractalfract9070463
APA StyleZhang, W., Li, L., Liu, Y., Wang, J., Li, Y., & Chen, G. (2025). Analytical Description of Three-Dimensional Fractal Surface Wear Process Based on Multi-Stage Contact Theory. Fractal and Fractional, 9(7), 463. https://doi.org/10.3390/fractalfract9070463






