Mathematical and Physical Analysis of the Fractional Dynamical Model
Abstract
1. Introduction
Truncated M-Fractional Derivative (TMFD)
2. Methodologies
2.1. Explanation of Modified Extended Function Technique
2.2. Explanation of Modified —Expansion Technique
3. Mathematical Analysis
3.1. Exact Solitons Through mEThF Technique
- Set 1:
3.2. Exact Wave Solitons via Modified Expansion Scheme
- Set 1:
- Set 2:
- Set 3:
- Set 4:
- Set 5:
- Set 6:
- Set 7:
- Set 8:
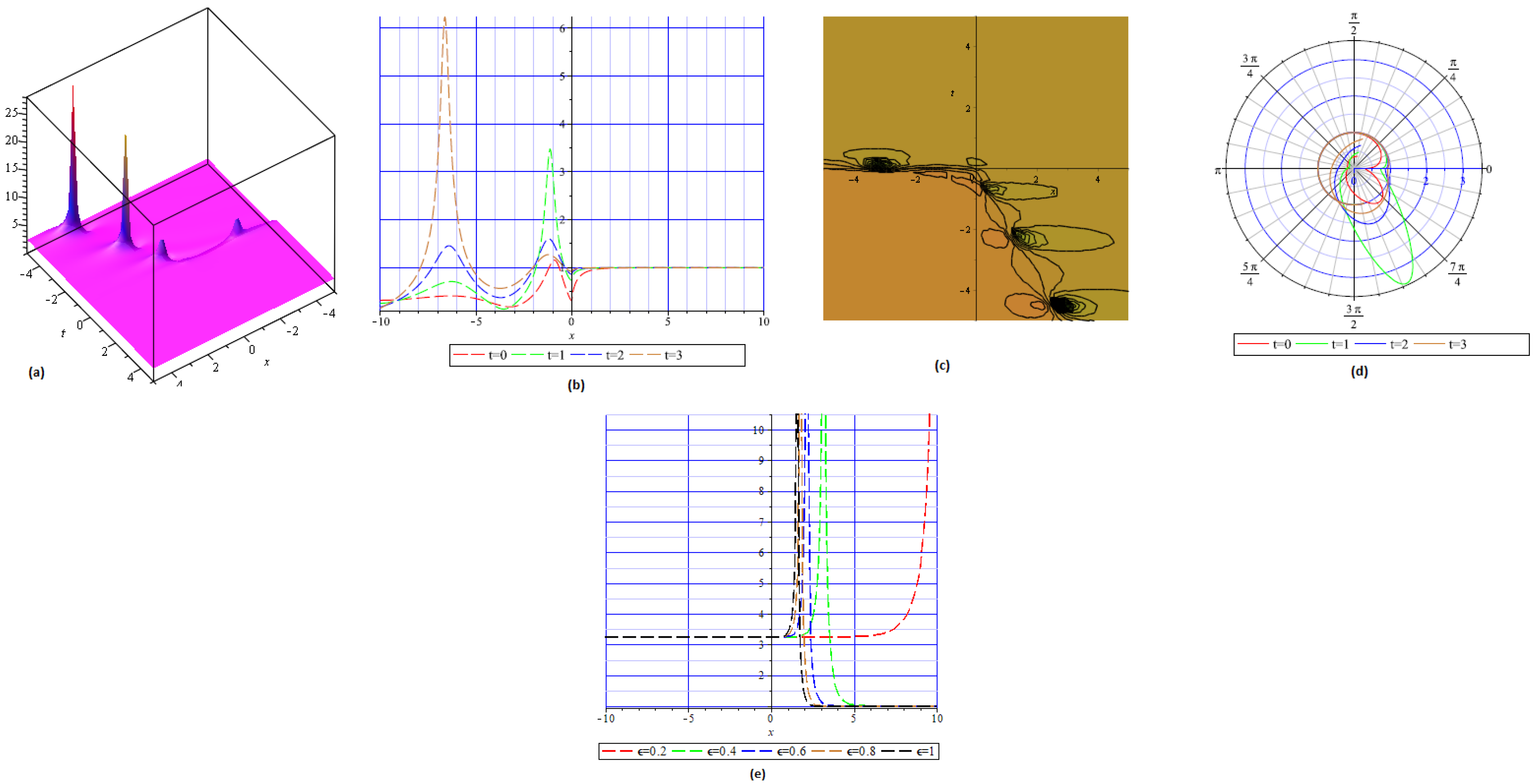
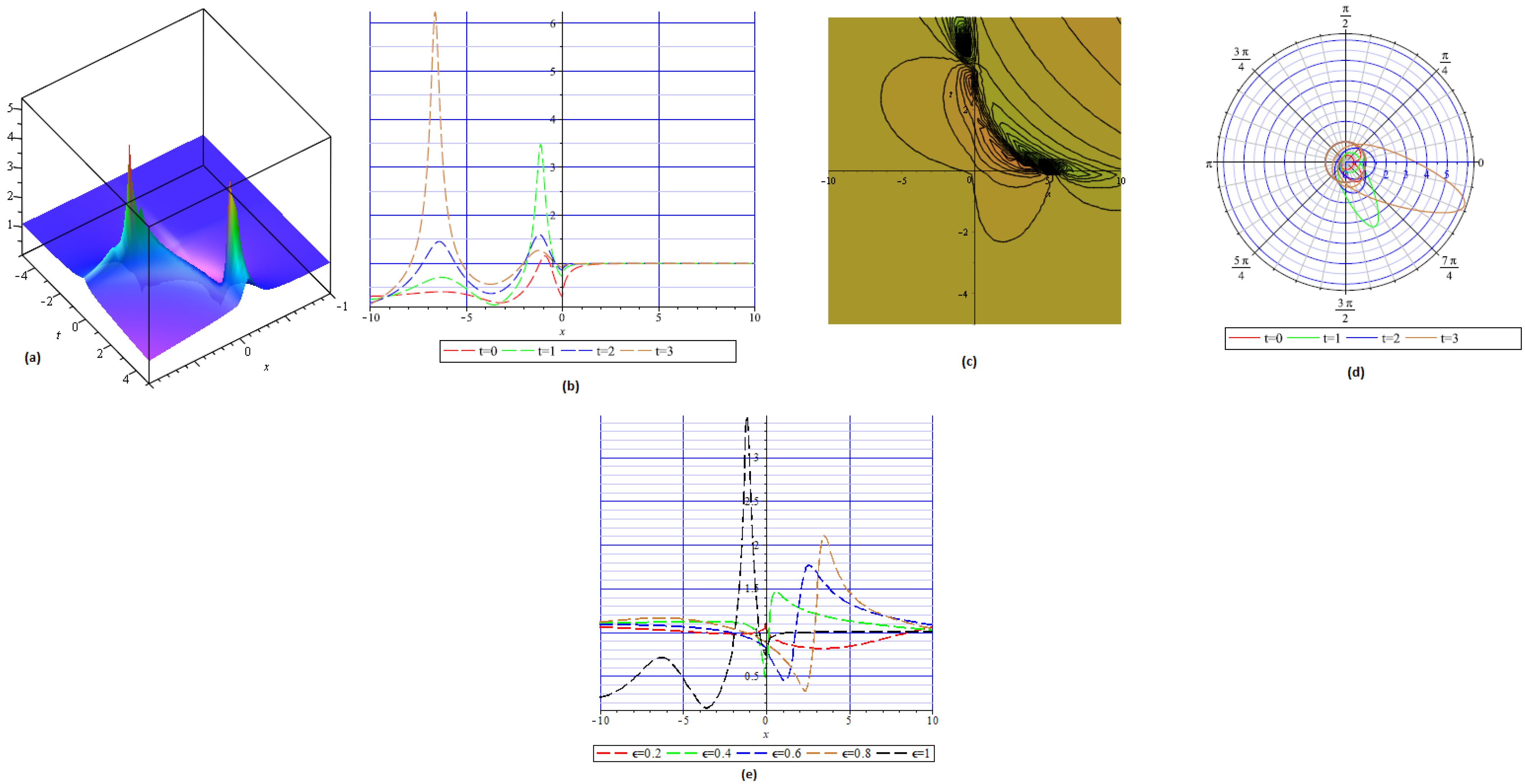
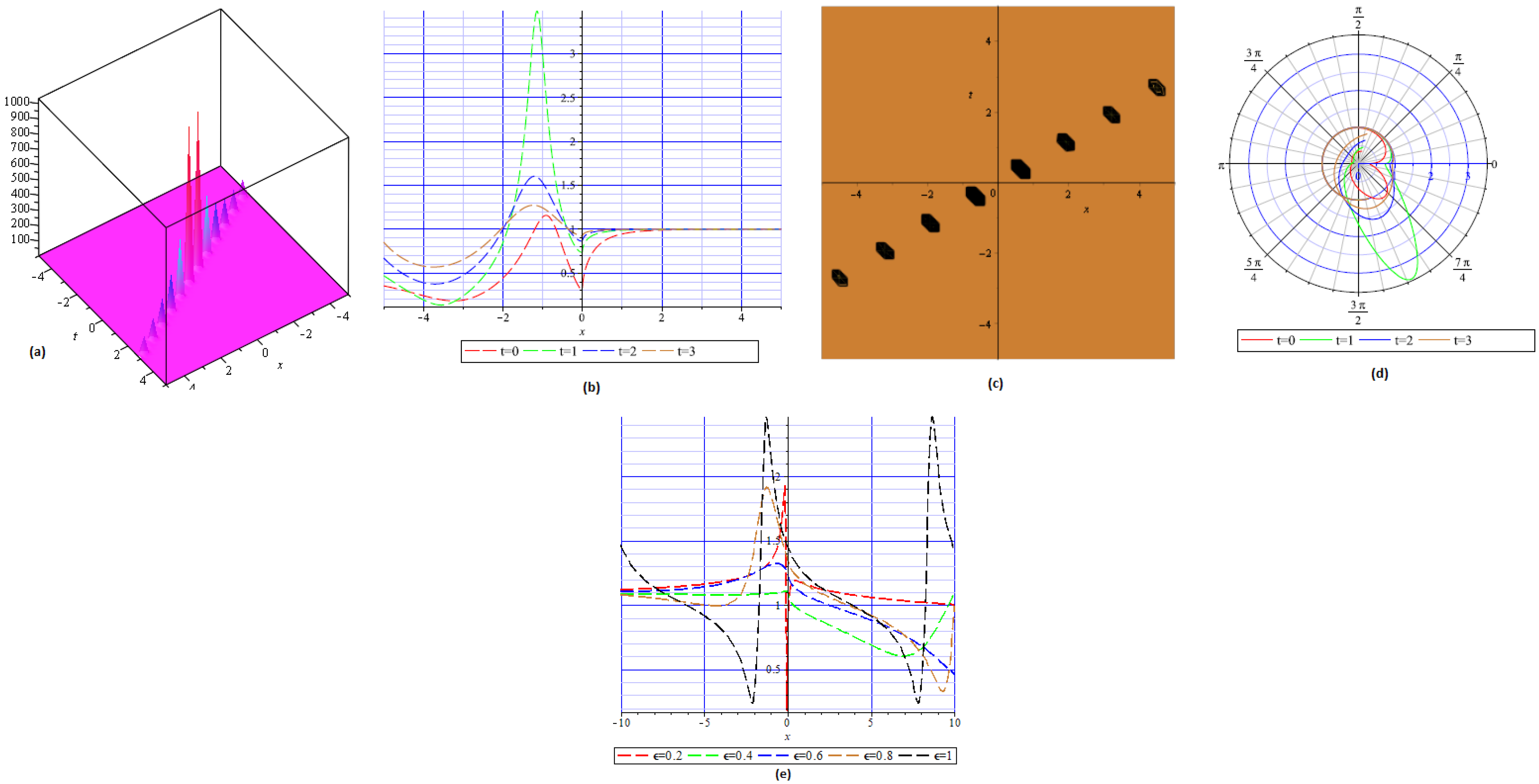
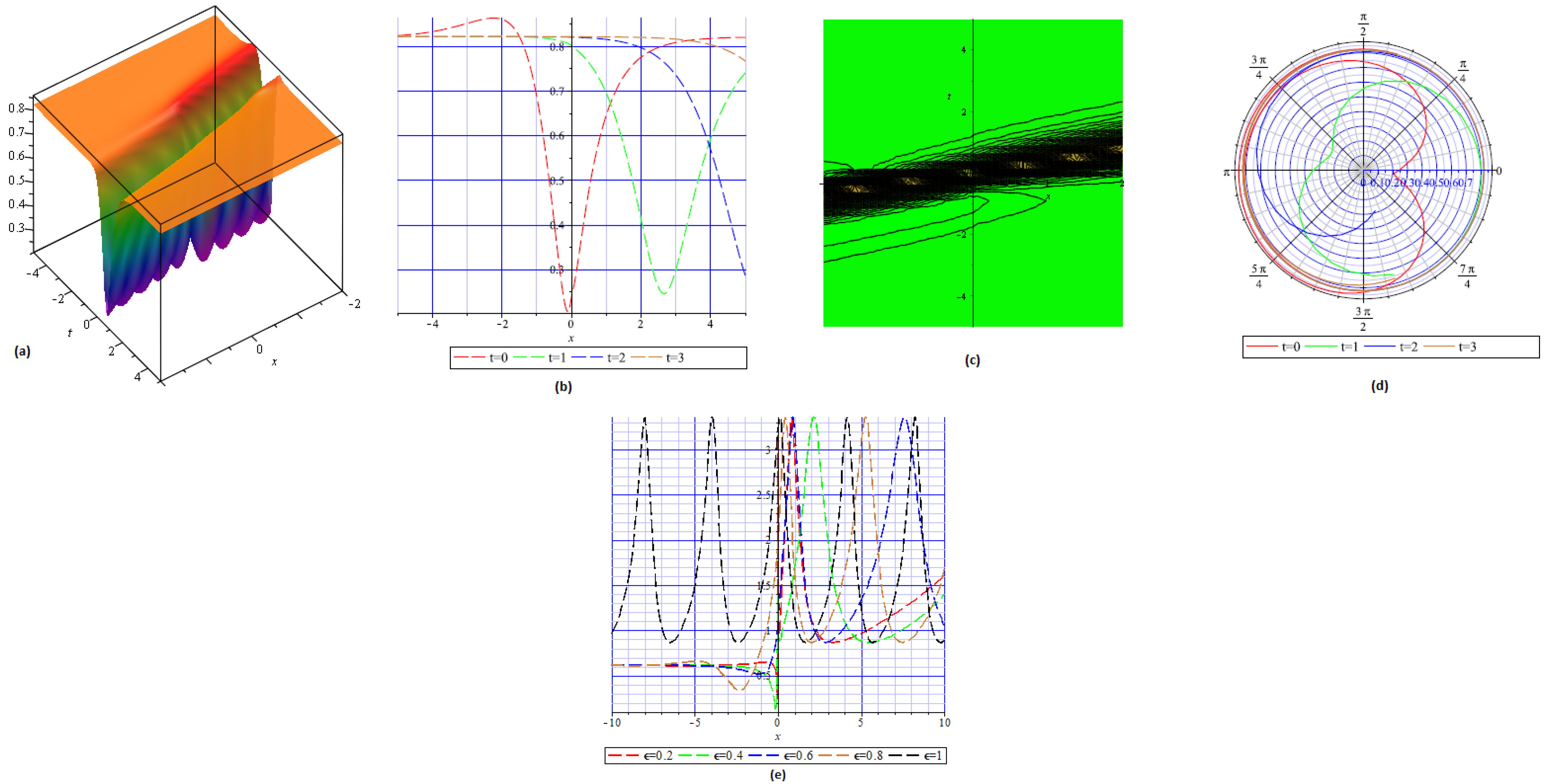
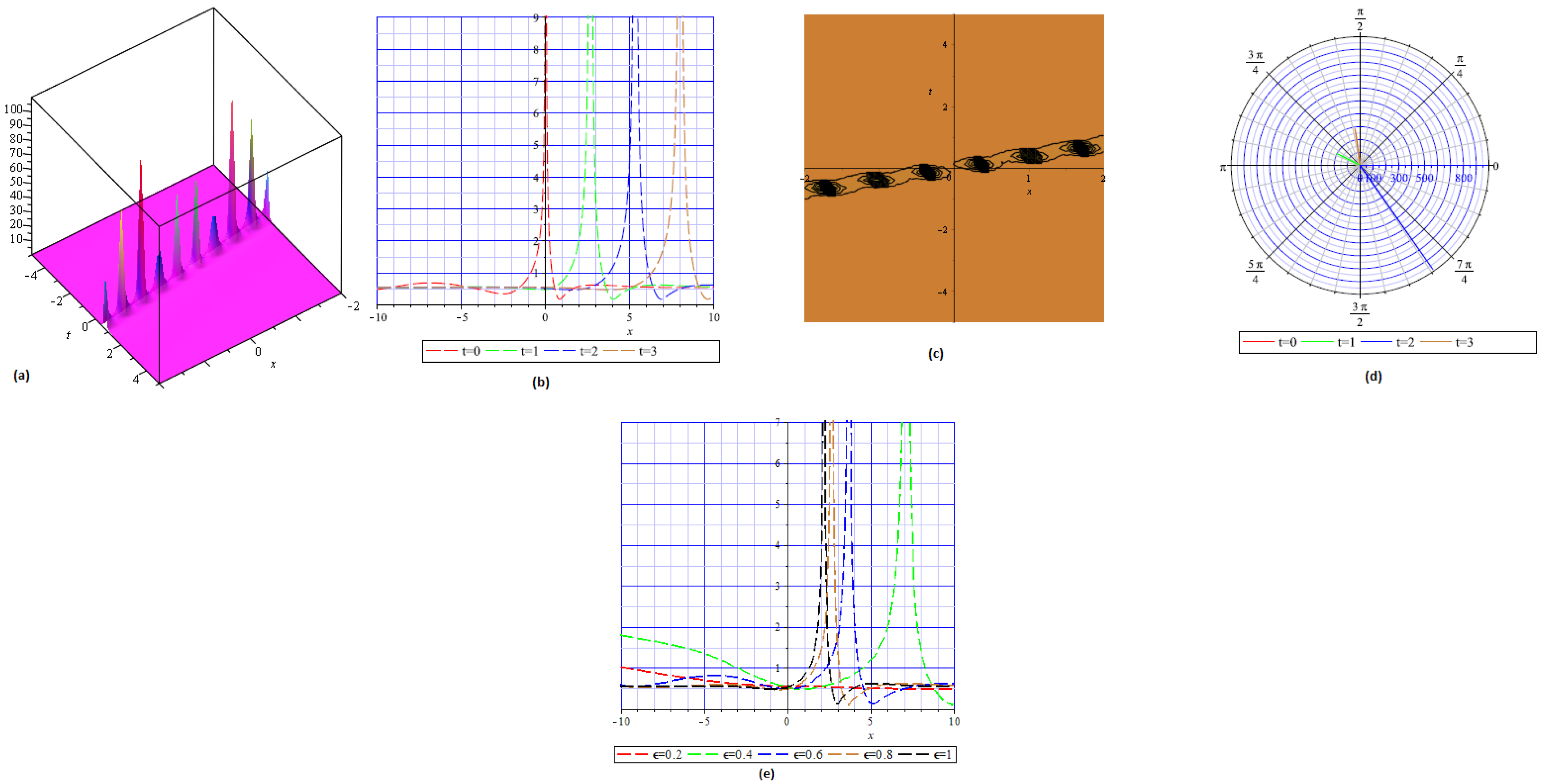
4. Physical Interpretation
5. MI Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raheel, M.; Zafar, A.; Razzaq, W.; Qousini, M. New analytical wave solitons and some other wave solutions of truncated M-fractional LPD equation along parabolic law of non-linearity. Opt. Quant. Electron. 2023, 55, 592. [Google Scholar] [CrossRef]
- Qawaqneh, H.; Zafar, A.; Raheel, M.; Zaagan, A.A.; Zahran, E.H.M.; Cevikel, A.; Bekir, A. New soliton solutions of M-fractional Westervelt model in ultrasound imaging via two analytical techniques. Opt. Quant. Electron. 2024, 56, 737. [Google Scholar] [CrossRef]
- Liu, C. The traveling wave solution and dynamics analysis of the fractional order generalized Pochhammer–Chree equation. AIMS Math. 2024, 9, 33956–33972. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Cesarano, C.; Iqbal, N.; Sidaoui, R.; E Ali, E. The exact solutions for the fractional Riemann wave equation in quantum mechanics and optics. Phys. Scr. 2024, 99, 085245. [Google Scholar] [CrossRef]
- Razzaq, W.; Alsharidi, A.K.; Zafar, A.; Alomair, M.A. Optical solitons to the beta-fractional density dependent diffusion-reaction model via three different techniques. Int. J. Mod. Phys. B 2023, 37, 2350268. [Google Scholar] [CrossRef]
- Abdou, M.A.; Soliman, A.A. Modified extended tanh-function method and its application on nonlinear physical equations. Phys. Lett. A 2006, 353, 487–492. [Google Scholar] [CrossRef]
- Zahran, E.H.; Khater, M.M. Modified extended tanh-function method and its applications to the Bogoyavlenskii equation. Appl. Math. Model. 2016, 40, 1769–1775. [Google Scholar] [CrossRef]
- Dubey, S.; Chakraverty, S. Application of modified extended tanh method in solving fractional order coupled wave equations. Math. Comput. Simul. 2022, 198, 509–520. [Google Scholar] [CrossRef]
- Rabie, W.B.; Ahmed, H.M.; Darwish, A.; Hussein, H.H. Construction of new solitons and other wave solutions for a concatenation model using modified extended tanh-function method. Alex. Eng. J. 2023, 74, 445–451. [Google Scholar] [CrossRef]
- Cinar, M.; Onder, I.; Secer, A.; Sulaiman, T.A.; Yusuf, A.; Bayram, M. Optical solitons of the (2+ 1)-dimensional Biswas–Milovic equation using modified extended tanh-function method. Optik 2021, 245, 167631. [Google Scholar] [CrossRef]
- Behera, S.; Behera, D. Nonlinear wave dynamics of (1+1)-dimensional conformable coupled nonlinear Higgs equation using modified (G′/G2)-expansion method. Phys. Scr. 2025. Available online: https://iopscience.iop.org/article/10.1088/1402-4896/adaa31 (accessed on 14 January 2025).
- Saboor, A.; Shakeel, M.; Liu, X.; Zafar, A.; Ashraf, M.A. comparative study of two fractional nonlinear optical model via modified (G′/G2)-expansion method. Opt. Quantum Electron. 2024, 56, 259. [Google Scholar] [CrossRef]
- Aljahdaly, N.H. Some applications of the modified (G′/G2)-expansion method in mathematical physics. Results Phys. 2019, 13, 102272. [Google Scholar] [CrossRef]
- Cevikel, A.C.; Bekir, A.; Abu Arqub, O.; Abukhaled, M. Solitary wave solutions of Fitzhugh–Nagumo-type equations with conformable derivatives. Front. Phys. 2022, 10, 1028668. [Google Scholar] [CrossRef]
- Tauseef Mohyud-Din, S.; Khan, Y.; Faraz, N.; Yıldırım, A. Exp-function method for solitary and periodic solutions of Fitzhugh-Nagumo equation. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 335–341. [Google Scholar] [CrossRef]
- Yokus, A. On the exact and numerical solutions to the FitzHugh–Nagumo equation. Int. J. Mod. Phys. B 2020, 34, 2050149. [Google Scholar] [CrossRef]
- Abdel-Aty, A.-H.; Khater, M.M.A.; Baleanu, D.; Khalil, E.M.; Bouslimi, J.; Omri, M. Abundant distinct types of solutions for the nervous biological fractional FitzHugh–Nagumo equation via three different sorts of schemes. Adv. Differ. Equ. 2020, 2020, 476. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yel, G.; Bulut, H. M-fractional solitons and periodic wave solutions to the Hirota-Maccari system. Mod. Phys. Lett. B 2019, 33, 1950052. [Google Scholar] [CrossRef]
- Sousa, J.V.D.; Oliveira, E.C.D. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar]
- Raslan, K.R.; Khalid, K.A.; Shallal, M.A. The modified extended tanh method with the Riccati equation for solving the space-time fractional EW and MEW equations. Chaos Solitons Fractals 2017, 103, 404–409. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Pang, J. Application of (G′/G2) Expansion Method for Solving Schrödinger’s Equation with Three-Order Dispersion. Adv. Appl. Math. 2017, 6, 212–217. [Google Scholar] [CrossRef]
- ur Rehman, S.; Ahmad, J. Modulation instability analysis and optical solitons in birefringent fibers to RKL equation without four wave mixing. Alex. Eng. J. 2021, 60, 1339–1354. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alomair, M.A.; Qawaqneh, H. Mathematical and Physical Analysis of the Fractional Dynamical Model. Fractal Fract. 2025, 9, 453. https://doi.org/10.3390/fractalfract9070453
Alomair MA, Qawaqneh H. Mathematical and Physical Analysis of the Fractional Dynamical Model. Fractal and Fractional. 2025; 9(7):453. https://doi.org/10.3390/fractalfract9070453
Chicago/Turabian StyleAlomair, Mohammed Ahmed, and Haitham Qawaqneh. 2025. "Mathematical and Physical Analysis of the Fractional Dynamical Model" Fractal and Fractional 9, no. 7: 453. https://doi.org/10.3390/fractalfract9070453
APA StyleAlomair, M. A., & Qawaqneh, H. (2025). Mathematical and Physical Analysis of the Fractional Dynamical Model. Fractal and Fractional, 9(7), 453. https://doi.org/10.3390/fractalfract9070453





