Discrete-Time Fractional-Order Sliding Mode Attitude Control of Multi-Spacecraft Systems Based on the Fully Actuated System Approach

Abstract

In practical applications, most systems operate based on digital signals obtained through sampling. Applying fractional-order control to spacecraft attitude control is meaningful for achieving better performance, especially in the coordination of the multi-spacecraft attitude system. In this paper, a discrete-time fractional-order sliding mode attitude control problem is studied for multi-spacecraft systems based on the fully actuated system approach. Firstly, a discrete-time disturbance observer based on the fractional-order theory is constructed to estimate the disturbance. Secondly, a discrete-time fractional-order sliding mode controller is designed by combining the transformed fully actuated discrete-time system and the disturbance observer. Subsequently, every spacecraft can track the desired attitude under the designed controller. Finally, the simulation results show that the developed control method achieves faster convergence, smaller overshoot, and higher control accuracy.

1. Introduction

Considering the future development needs of space missions, the control of multi-spacecraft systems has received extensive attention in the past decade. As people aim to explore more distant destinations and undertake complex tasks such as satellite servicing and formation flying, the effective coordination and control of multi-spacecraft systems have become critical. For instance, Sui and Duan et al. [1] investigated a novel integral sliding mode approach to converge tracking errors within a fixed time. Cui and Zhang et al. [2] designed a fixed-time adaptive controller for multiple spacecraft systems on a directed graph. Other scholars have made many profound contributions to the attitude cooperative control of multi-spacecraft systems [3,4,5,6]. Furthermore, some remarkable advances have been achieved in broader applications of multi-agent systems. In [7], an unknown-input-observer scheme was proposed to resolve delay issues in multi-UAV systems, achieving robust $H_{\infty }$ consensus tracking. Wu and Sun et al. [8] designed a PD-like consensus tracking algorithm to achieve quick convergence under noisy binary communication and time-varying leader states. Chang and Yang et al. [9] developed a formation strategy for a heterogeneous system, improving formation maintenance and obstacle avoidance capabilities. These studies investigate multi-agent system control through diverse control approaches, spanning both continuous-time and discrete-time controllers.

Although traditional continuous-time controller designs are relatively convenient, control signals and system state variables are acquired through sampled data in most practical implementations [10]. Therefore, it is necessary to study discrete-time controllers. The development of discrete-time spacecraft attitude systems has received relatively less attention. Nevertheless, some efforts have been devoted to this field. In [11], the scholars studied a discrete-time state observer for a rigid-spacecraft system. Lee and Park et al. [12] presented an optimal formation tracking control method on the basis of discrete-time Hamilton–Jacobi theory. For a spacecraft with momentum and control constraints, Phogat and Chatterjee et al. [13] addressed the attitude optimal control problem. Discrete-time control has the advantages of lower cost in implementation and relatively simpler computation. Therefore, it is meaningful to further investigate discrete-time spacecraft attitude systems.

However, the spacecraft attitude system is a coupled nonlinear system, which poses challenges for relevant controller design. In response to the issues associated with nonlinear systems, Duan [14] proposed the fully actuated system approach. This approach greatly reduces the complexity of designing controllers for nonlinear systems and enables more flexible and robust controller design. Moreover, Duan [15] pointed out that this approach was not only effective for continuous-time systems but can also be adaptable to discrete-time systems. For example, Wang and Duan et al. [16] designed a predictive controller for a discrete-time nonlinear model based on the fully actuated approach. The discrete-time higher-order fully actuated system approach can reduce the complexity of controller design while enhancing the system’s robustness. Therefore, it is worth extending further research towards discrete-time nonlinear systems through the fully actuated system approach.

Most systems are inevitably subjected to the disturbances during their operation. Therefore, it is necessary to adopt a suitable control method to ensure stability. Under conditions of model inaccuracy and disturbances, PID-based regulation constitutes a widely adopted approach for stabilizing uncertain systems. Model-free controllers offer implementation simplicity and design convenience, particularly in real application systems. However, for systems with well-characterized models, model-based methods are generally preferred to achieve enhanced control precision. Sliding mode control, as a traditional model-based approach in the field of control systems, is well known for its excellent robustness and insensitivity to parameter variations [17,18]. Over the years, many studies have been carried out on sliding mode control methods for spacecraft systems. Chen and Yan et al. [19] proposed a discrete-time sliding mode control law to achieve spacecraft attitude tracking in finite time. For a prescribed time spacecraft attitude tracking problem, a sliding mode controller based on a disturbance observer was proposed to achieve attitude tracking [20]. Tan and Zhang et al. [21] designed an event-triggered sliding mode controller for spacecraft with attitude constraints. In addition, there is a growing need for tighter control of accuracy in the future. For the above requirements, fractional-order control is an effective method. Fractional-order control is based on fractional-order theory and utilizes the historical state information of the system to achieve more accurate control performance [22,23,24,25]. In recent years, considerable advances have been made in the development and application of fractional-order control methods. Sopasakis and Sarimveis [26] utilized discrete-time fractional-order theory in the control field. Sun and Ma et al. [27] designed a discrete-time fractional-order sliding mode for a linear motor tracking problem. Zhang and Yang et al. [28] investigated an optimal setting of the discrete-time fractional-order PID controller. In [29], a fractional-order PI controller for multi-area power systems was designed to achieve better control performance. Gupta and Dei et al. [30] developed a fractional-order PID controller to achieve optimal performance for power systems. Shao and Chen [31] proposed a robust discrete-time fractional-order controller for an unmanned aerial vehicle system. Wu and Liu et al. [32] developed a fractional-order sliding mode control strategy which can achieve a faster attitude coordination speed. As a result, exploring the application of fractional-order control in a multi-spacecraft system is worth further investigation.

Therefore, inspired by the above ideas, a discrete-time fractional-order sliding mode control method based on the fully actuated system approach is studied for a multi-spacecraft attitude system with bounded disturbances in this paper. The main contributions of this paper are summarized as follows:

• The proposed method combines the discrete-time fully actuated system approach with fractional-order control theory, and a sliding mode controller is developed to enable each spacecraft to track the desired attitude for the multi-spacecraft attitude system.
• Based on the fractional-order theory, a fractional-order discrete-time disturbance observer is designed to estimate the unknown disturbances, and the observer can complete the estimation of the disturbances.
• Based on the Lyapunov theory and simulations, the boundedness of the observer estimation error and the attitude consensus of the multi-spacecraft system are proven.

The structure of the paper is as follows: In Section 2 are the problem statement and preliminaries. The discrete-time disturbance observer based on fractional-order theory is designed in Section 3. In Section 4, a discrete-time fractional-order sliding mode controller is designed based on the fully actuated system approach, and the simulation results are demonstrated in Section 5. The Conclusions are summarized in Section 6.

2. Problem Statement and Preliminaries

Considering N spacecraft with disturbances, their simplified continuous-time attitude systems are governed by [33]

$$\begin{array}{cc}& {\overline{\mathcal{O}}}_i\left({\sigma }_i\right){\ddot{\sigma }}_i+{\overline{\mathcal{K}}}_i({\sigma }_i,{\dot{\sigma }}_i){\dot{\sigma }}_i={\mathcal{J}}^{-\mathrm{T}}\left({\sigma }_i\right)(u_i+{\mathrm{d}}_i)\hfill \\ & {\overline{\mathcal{O}}}_i\left({\sigma }_i\right)={\mathcal{J}}^{-\mathrm{T}}\left({\sigma }_i\right){\mathcal{M}}_i{\mathcal{J}}^{-1}\left({\sigma }_i\right)\hfill \\ & {\overline{\mathcal{K}}}_i({\sigma }_i,{\dot{\sigma }}_i)=-{\mathcal{J}}^{-\mathrm{T}}\left({\sigma }_i\right){\mathcal{M}}_i{\mathcal{J}}^{-1}\left({\sigma }_i\right)\dot{\mathcal{J}}\left({\sigma }_i\right){\mathcal{J}}^{-1}\left({\sigma }_i\right)\hfill \\ & -{\mathcal{J}}^{-\mathrm{T}}\left({\sigma }_i\right){\left({\mathcal{M}}_i{\mathcal{J}}^{-1}\left({\sigma }_i\right){\dot{\sigma }}_i\right)}^{\times }{\mathcal{J}}^{-1}\left({\sigma }_i\right)\hfill \end{array}$$

(1)

where $i=1,2,3,\dots ,N$, ${\sigma }_i={[{\sigma }_{i1},{\sigma }_{i2},{\sigma }_{i3}]}^{\mathrm{T}}$ represents the attitude based on modified Rodrigues parameters of the ith spacecraft, ${\left(·\right)}^{\times }$ denotes the skew-symmetric matrix of a vector, $\mathcal{J}\left({\sigma }_i\right)={\displaystyle \frac{1}{4}}\left(1-{\sigma }_i^T{\sigma }_i\right)I_3+{\displaystyle \frac{1}{2}}{\sigma }_i^{\times }+{\displaystyle \frac{1}{2}}{\sigma }_i{\sigma }_i^T\in {\Re }^{3\times 3}$, ${\mathcal{M}}_i\in {\Re }^{3\times 3}$ is the known mass matrix, $u_i$ is the control input, and ${\mathrm{d}}_i$ is the external disturbance.

To depict the communication topology of multi-spacecraft system, Lu [34] introduced the fundamental principles and notations from graph theory. Considering a multi-spacecraft attitude formation system consisting of N spacecraft, its communication topology can be illustrated by an N-order undirected weighted graph $G_c=\left\{\mathcal{V},\mathcal{E},A\right\}$. Then, each spacecraft denotes a node in the diagram, $\mathcal{V}=\left\{1,2,3,\dots ,N\right\}$ describes the set of spacecraft, $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ represents the set of edges, $(i,j)\in \mathcal{E}$ indicates that the node i can obtain the status information of the node j. For the case $G_c$ is an undirected graph, $(j,i)\in \mathcal{E}$ holds if $(i,j)\in \mathcal{E}$. The neighbor set of node i is described as ${\Omega }_i=\left\{j\in \mathcal{V}:(i,j)\in \mathcal{E}\right\}$. The adjacency matrix is defined as $A=\left\{a_{ij}\right\}$, where $a_{ij}$ is the connection weight. If $j\in {\Omega }_i$, then $a_{ij}=1$, otherwise $a_{ij}=0$. The degree matrix is expressed as $\mathcal{D}=\mathrm{diag}\{{\mathcal{D}}_1,{\mathcal{D}}_2,\dots ,{\mathcal{D}}_N\}$, where ${\mathcal{D}}_i={\displaystyle \sum _{j\in {\Omega }_i}}{a}_{ij}$. Then, the Laplacian matrix L is defined as $L=\mathcal{D}-A$. The multi-agent system has a virtual leader, which is labeled as 0. Let $B=\left\{b_i\right\}$, and $b_i$ is the connection weight between the ith spacecraft and the leader.

To study the discrete-time sliding mode control, the continuous-time system (1) is transformed into an approximative discrete-time system through the Euler approximation, which is proposed in [35]. The transformed discrete-time system can be written as

$$\begin{array}{c}\hfill \begin{array}{c}\begin{array}{cc}& {\mathcal{Y}}_i(k+1)={\mathcal{Y}}_i\left(k\right)+T_0{\mathcal{X}}_i\left(k\right)\hfill \\ & {\mathcal{X}}_i(k+1)={\mathcal{X}}_i\left(k\right)+T_0({\Gamma }_i{\mathcal{X}}_i\left(k\right)+{\mathcal{G}}_i{u}_i\left(k\right)+d_i\left(k\right))\hfill \end{array}\hfill \end{array}\end{array}$$

(2)

where ${\mathcal{Y}}_i\left(k\right)={[{\sigma }_{i1}\left(k\right),{\sigma }_{i2}\left(k\right),{\sigma }_{i3}\left(k\right)]}^{\mathrm{T}}$ and ${\mathcal{X}}_i\left(k\right)={[{\dot{\sigma }}_{i1}\left(k\right),{\dot{\sigma }}_{i1}\left(k\right),{\dot{\sigma }}_{i3}\left(k\right)]}^{\mathrm{T}}$, $T_0$ denotes the discrete sample time, ${\Gamma }_i=-{\overline{\mathcal{O}}}_i^{-1}\left({\mathcal{Y}}_i\left(k\right)\right){\overline{\mathcal{K}}}_i({\mathcal{Y}}_i\left(k\right),{\mathcal{X}}_i\left(k\right))\in {\Re }^{3\times 3}$ and ${\mathcal{G}}_i={\overline{\mathcal{O}}}_i^{-1}\left({\mathcal{Y}}_i\left(k\right)\right){\mathcal{J}}^{-\mathrm{T}}\left({\mathcal{Y}}_i\left(k\right)\right)\in {\Re }^{3\times 3}$, $d_i\left(k\right)={\mathcal{G}}_i{\mathrm{d}}_i\left(k\right)+{\Xi }_i$ is the composite disturbance, and ${\Xi }_i$ is the discretization error.

Remark 1.

According to [36,37], we can know that the rigid-body spacecraft satisfies the local Lipschitz condition. So, it can be inferred that $∥\Xi ∥\le d_e$ from [19], where $d_e$ is a bounded constant. In this condition, the discretization error Ξ can be considered as the disturbance.

In this paper, a discrete-time fractional-order sliding mode control method combined with a disturbance observer is proposed for the spacecraft system (1). The control objective is to design a discrete-time fractional-order sliding mode controller such that all followers can track the desired attitude signal ${\mathcal{Y}}_0\left(k\right)$ within a bounded range under the disturbance, where the desired signal ${\mathcal{Y}}_0\left(k\right)$ is a known function vector. Figure 1 and Figure 2 show the control system block diagram.

To facilitate the design of the control method, the following definitions, lemmas, and assumptions are introduced in this paper:

Definition 1

([26]). The discrete-time fractional-order Grünwald–Letnikow difference operator ${\nabla }^{\gamma }$ with zero initial time for the function $f\left(k\right)$ given as follows:

$$\begin{array}{c}\hfill {\nabla }^{\gamma }f\left(k\right)=\sum _{j=0}^k{(-1)}^j\left(\begin{array}{c}\gamma \hfill \\ j\hfill \end{array}\right)f(k-j)\end{array}$$

(3)

where the fractional order γ denotes the set of positive real numbers with $0<\gamma \le 1$ and the binomial coefficient $\left(\begin{array}{c}\gamma \hfill \\ j\hfill \end{array}\right)$ can be written as

$$\begin{array}{c}\hfill \left(\begin{array}{c}\gamma \hfill \\ j\hfill \end{array}\right)=\left\{\begin{array}{c}1j=0\hfill \\ {\displaystyle \frac{\gamma (\gamma -1)\dots (\gamma -j+1)}{j!}}j>0\hfill \end{array}\right.\end{array}$$

(4)

Definition 2

([38]). The fractional sum of the γ order is defined by

$$\begin{array}{c}\hfill {\nabla }^{-\gamma }f\left(k\right)=\sum _{j=0}^k\left\{\begin{array}{c}\gamma \\ k-j\end{array}\right\}f\left(j\right)\end{array}$$

(5)

where the binomial coefficient $\left\{\begin{array}{c}\gamma \\ k-j\end{array}\right\}$ can be written as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\gamma \\ k-j\end{array}\right\}=\left\{\begin{array}{cc}1& k-j=0\\ {\displaystyle \frac{\gamma (\gamma +1)\dots (\gamma +k-j-1)}{(k-j)!}}& k-j>0\end{array}\right.\end{array}$$

(6)

Definition 3

([15]). Considering the discrete-time model as follows:

$$\left\{\begin{array}{c}{x}_1\left(k+1\right)=f_1\left(x_n\left(k\right),u\left(k\right)\right)\hfill \\ x_2\left(k+1\right)=f_2\left(x_1\left(k\right),x_n\left(k\right),u\left(k\right)\right)\hfill \\ x_3\left(k+1\right)=f_3\left(x_{1\sim 2}\left(k\right),x_n\left(k\right),u\left(k\right)\right)\hfill \\ ⋮\hfill \\ x_{n-1}\left(k+1\right)=f_{n-1}\left(x_{1\sim n-1}\left(k\right),x_n\left(k\right),u\left(k\right)\right)\hfill \\ x_n\left(k+1\right)=f_n\left(x_{1\sim n}\left(k\right)\right)+\aleph \left(x_{1\sim n}\left(k\right)\right)u\left(k\right),\hfill \end{array}\right.$$

(7)

where $x_i$, $i=1,2,\dots n$ are system state vectors, u is a system control vector, $f_i\left(·\right)$ are a series of vector functions, and $\aleph \left(·\right)$ is a nonlinear matrix function.

If $det\aleph \left(x_{1\sim n}\left(k\right)\right)\ne 0$, then the system (7) satisfies the fully actuated condition.

Lemma 1

([38]). For the positive real numbers ${\gamma }_0$ and ${\gamma }_1$, we have

$$\begin{array}{c}\hfill {\nabla }^{{\gamma }_0}{\nabla }^{-{\gamma }_1}f\left(k\right)={\nabla }^{{\gamma }_0-{\gamma }_1}f\left(k\right)\end{array}$$

(8)

Specifically, one has that ${\nabla }^{0}f\left(k\right)=f\left(k\right)$.

Lemma 2

([31]). For the bounded vector $\epsilon \left(k\right)$ and $0<{\gamma }^{\prime }<1$, $∥{\nabla }^{{\gamma }^{\prime }}\epsilon \left(k\right)∥$ is also bounded.

Assumption 1

([31]). The unknown disturbance $d_i\left(k\right)$ is bounded. Therefore, $\Delta d_i\left(k\right)$ is bounded and $\Delta d_i\left(k\right)=d_i(k+1)-d_i\left(k\right)=T_0{\varpi }_i\left(k\right)$, ${\varpi }_i\left(k\right)$ is an unknown bounded variable.

Assumption 2.

The discrete-time form of the trajectory satisfies ${\mathcal{Y}}_0(k+1)={\mathcal{Y}}_0\left(k\right)+T_0{\mathcal{X}}_0\left(k\right)$ and ${\mathcal{X}}_0(k+1)={\mathcal{X}}_0\left(k\right)+T_0{\alpha }_0\left(k\right)$. ${\alpha }_0\left(k\right)$ is a known bounded signal vector.

Assumption 3.

The multi-spacecraft communication topology is a connected undirected graph.

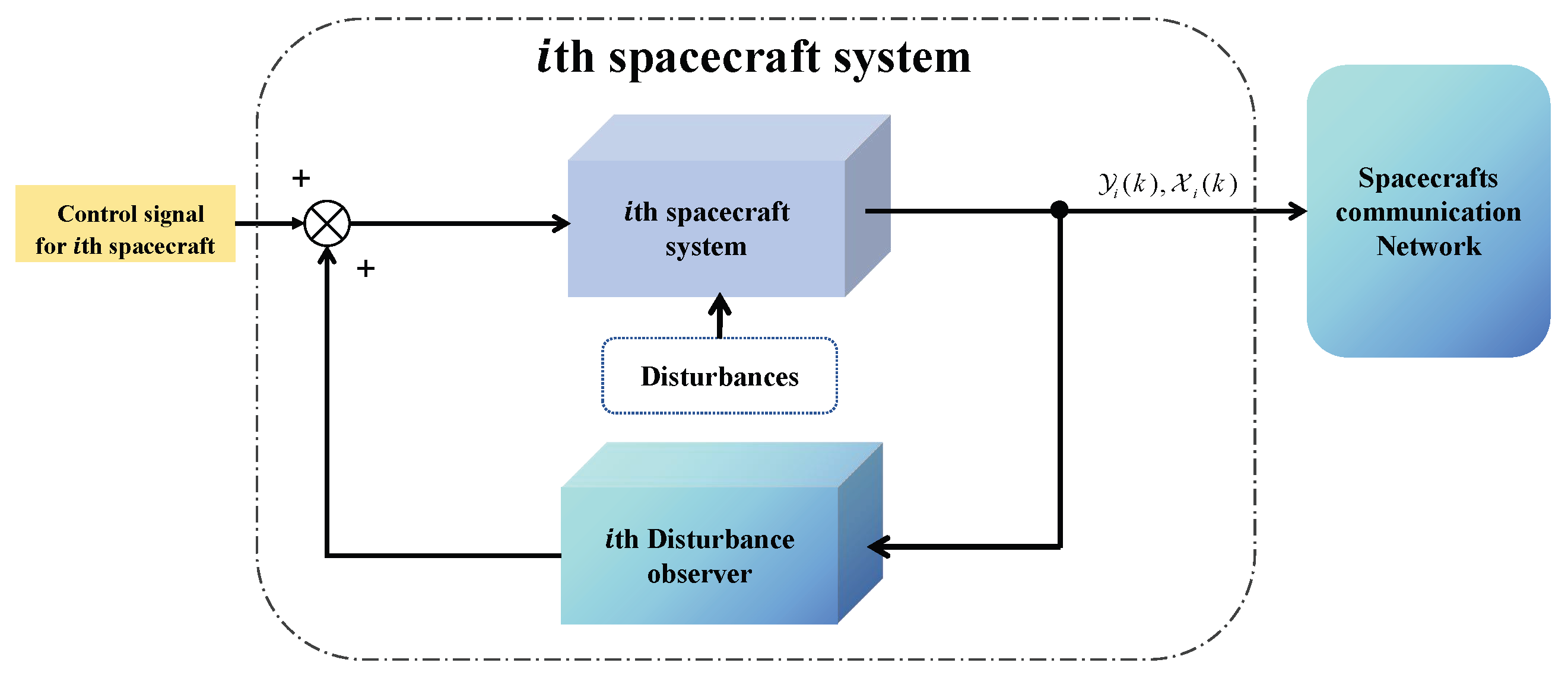
3. Discrete-Time Disturbance Observer Design

In this part, considering that the disturbance will affect the control performance of the spacecraft, it is necessary to design the corresponding disturbance observer to mitigate the impact of the disturbance.

For the discrete-time attitude system (2), we design the disturbance observer based on the fractional-order theory in the following form:

$$\begin{array}{cc}& {\mathcal{N}}_i\left(k\right)={\mathcal{X}}_i\left(k\right)-{\widehat{\mathcal{X}}}_i\left(k\right)-\lambda {\nabla }^{{\gamma }_1-1}({\mathcal{X}}_i(k-1)-{\widehat{\mathcal{X}}}_i(k-1))\hfill \\ & {\widehat{\mathcal{X}}}_i(k+1)={\widehat{\mathcal{X}}}_i\left(k\right)+T_0({\Gamma }_i{\mathcal{X}}_i\left(k\right)+{\mathcal{G}}_i{u}_i\left(k\right)+{\widehat{d}}_i\left(k\right))-\lambda {\nabla }^{{\gamma }_1}({\mathcal{X}}_i\left(k\right)-{\widehat{\mathcal{X}}}_i\left(k\right))\hfill \\ & {\widehat{d}}_i\left(k\right)={\mathcal{KN}}_i\left(k\right)\hfill \end{array}$$

(9)

where ${\mathcal{N}}_i\left(k\right)$ is the ith observer auxiliary vector, ${\widehat{d}}_i\left(k\right)$ represents the estimated value of the disturbance of the ith observer, ${\gamma }_1$ is the fractional-order parameter, $\lambda =\mathrm{diag}[{\lambda }_1,{\lambda }_2,{\lambda }_3]$ and $\mathcal{K}=\mathrm{diag}[{\mathcal{K}}_1,{\mathcal{K}}_2,{\mathcal{K}}_3]$ are the designed positive diagonal matrices.

Theorem 1.

If the designed diagonal matrices λ, $\mathcal{K}$, and discrete sample time $T_0$ makes $[1-{(1-{\mathcal{K}}_i{T}_0)}^2-{\displaystyle \frac{{\lambda }_i{T}_0}{2}}]>0$ and $1-{\mathcal{K}}_i{T}_0>0$, then the discrete-time disturbance observer can complete the estimation of the disturbance $d_i\left(k\right)$.

Proof. 

We define ${\tilde{d}}_i(k+1)=d(k+1)-{\widehat{d}}_i(k+1)$ and $\Delta {\tilde{d}}_i(k+1)={\tilde{d}}_i(k+1)-{\tilde{d}}_i\left(k\right)$. According to (9) and Assumption 1, we have

$$\begin{array}{cc}\hfill \Delta {\tilde{d}}_i(k+1)& =d_i(k+1)-d_i\left(k\right)-({\widehat{d}}_i(k+1)-{\widehat{d}}_i\left(k\right))\hfill \\ & =T_0\varpi \left(k\right)-\mathcal{K}({\mathcal{N}}_i\left(k+1\right)-{\mathcal{N}}_i\left(k\right))\hfill \end{array}$$

(10)

Substituting (9) into (10), and according to Lemma 1, we can obtain that

$$\begin{array}{cc}\hfill {\mathcal{N}}_i(k+1)-{\mathcal{N}}_i\left(k\right)=& \left[\left({\mathcal{X}}_i(k+1)-{\mathcal{X}}_i\left(k\right)\right)-\left({\widehat{\mathcal{X}}}_i(k+1)-{\widehat{\mathcal{X}}}_i\left(k\right)\right)\right]\hfill \\ \hfill & -\lambda {\nabla }^{{\gamma }_1-1}({\mathcal{X}}_i\left(k\right)-{\widehat{\mathcal{X}}}_i\left(k\right))+\lambda {\nabla }^{{\gamma }_1-1}({\mathcal{X}}_i(k-1)-{\widehat{\mathcal{X}}}_i(k-1))\hfill \\ \hfill =& T_0{\tilde{d}}_i\left(k\right)+\lambda {\nabla }^{{\gamma }_1}({\mathcal{X}}_i\left(k\right)-{\widehat{\mathcal{X}}}_i\left(k\right))-\lambda {\nabla }^{{\gamma }_1-1}({\mathcal{X}}_i\left(k\right)-{\widehat{\mathcal{X}}}_i\left(k\right))\hfill \\ \hfill & +\lambda {\nabla }^{{\gamma }_1-1}({\mathcal{X}}_i(k-1)-{\widehat{\mathcal{X}}}_i(k-1))\hfill \\ \hfill =& T_0{\tilde{d}}_i\left(k\right)+\lambda {\nabla }^{{\gamma }_1}({\mathcal{X}}_i\left(k\right)-{\widehat{\mathcal{X}}}_i\left(k\right))\hfill \\ \hfill & -\lambda {\nabla }^{{\gamma }_1-1}\left[({\mathcal{X}}_i\left(k\right)-{\mathcal{X}}_i(k-1))-({\widehat{\mathcal{X}}}_i\left(k\right)-{\widehat{\mathcal{X}}}_i(k-1))\right]\hfill \\ \hfill =& T_0{\tilde{d}}_i\left(k\right)+\lambda {\nabla }^{{\gamma }_1}({\mathcal{X}}_i\left(k\right)-{\widehat{\mathcal{X}}}_i\left(k\right))-\lambda {\nabla }^{{\gamma }_1-1}\left[{\nabla }^1{\mathcal{X}}_i\left(k\right)-{\nabla }^1{\widehat{\mathcal{X}}}_i\left(k\right)\right]\hfill \\ \hfill =& T_0{\tilde{d}}_i\left(k\right)\hfill \end{array}$$

(11)

Then, it can be deduced that

$$\Delta {\tilde{d}}_i(k+1)=T_0{\varpi }_i\left(k\right)-T_0\mathcal{K}{\tilde{d}}_i\left(k\right)$$

(12)

Choosing the Lyapunov function as:

$$V_o\left(k\right)={\tilde{d}}_i^{\mathrm{T}}\left(k\right)\tilde{O}{\tilde{d}}_i\left(k\right)$$

(13)

where $\tilde{O}$ is a positive diagonal matrix.

From (12), it can be deduced that

$$\begin{array}{cc}\hfill V_o(k+1)& ={\tilde{d}}_i^{\mathrm{T}}(k+1)\tilde{O}{\tilde{d}}_i(k+1)\hfill \\ & =\sum _{n=1}^3{\tilde{o}}_n{(T_0{\varpi }_{i,n}\left(k\right)+(1-{\mathcal{K}}_n{T}_0){\tilde{d}}_{i,n}\left(k\right))}^2\hfill \\ & =\sum _{n=1}^3{\tilde{o}}_n[T_0^2{\varpi }_{i,n}^2\left(k\right)+{(1-{\mathcal{K}}_n{T}_0)}^2{\tilde{d}}_{i,n}^2\left(k\right)+2(1-{\mathcal{K}}_n{T}_0)T_0{\varpi }_{i,n}\left(k\right){\tilde{d}}_{i,n}\left(k\right)]\hfill \end{array}$$

(14)

where ${\tilde{o}}_n$ represents the nth element of $\tilde{O}$, ${\tilde{d}}_{i,n}\left(k\right)$ is the nth element of ${\tilde{d}}_i\left(k\right)$, and ${\varpi }_{i,n}\left(k\right)$ is the nth element of ${\varpi }_i\left(k\right)$.

Defining $\Delta V_o\left(k\right)=V_o(k+1)-V_o\left(k\right)$, we can know

$$\begin{array}{cc}\hfill \Delta V_o\left(k\right)=& \sum _{n=1}^3{\tilde{o}}_n[T_0^2{\varpi }_{i,n}\left(k\right)+({(1-{\mathcal{K}}_n{T}_0)}^2-1){\tilde{d}}_{i,n}^2\left(k\right)\hfill \\ & +2(1-{\mathcal{K}}_n{T}_0)T_0{\varpi }_{i,n}\left(k\right){\tilde{d}}_{i,n}\left(k\right)\left)\right]\hfill \end{array}$$

(15)

According to Young’s inequality, it can be inferred that

$$2{\varpi }_{i,n}\left(k\right){\tilde{d}}_{i,n}\left(k\right)\le {\displaystyle \frac{2(1-{\mathcal{K}}_n{T}_0)}{{\lambda }_n}}{\varpi }_{i,n}^2\left(k\right)+{\displaystyle \frac{{\lambda }_n}{2(1-{\mathcal{K}}_n{T}_0)}}{\tilde{d}}_{i,n}^2\left(k\right)$$

(16)

Thus, the following inequality can be drawn

$$\begin{array}{cc}\hfill \Delta V_o\left(k\right)\le & \sum _{n=1}^3{\tilde{o}}_n[T_0^2{\varpi }_{i,n}^2\left(k\right)+({(1-{\mathcal{K}}_n{T}_0)}^2-1+{\displaystyle \frac{{\lambda }_n{T}_0}{2}}){\tilde{d}}_{i,n}^2\left(k\right)\hfill \\ & +2{\displaystyle \frac{{(1-{\mathcal{K}}_n{T}_0)}^2{T}_0}{{\lambda }_n}}{\varpi }_{i,n}^2\left(k\right)\left)\right]\hfill \\ \hfill \le & -\sum _{n=1}^3{\tilde{o}}_n{\mathcal{C}}_n{\tilde{d}}_{i,n}^2\left(k\right)+\sigma \hfill \\ \hfill \le & -{\mathcal{C}}_{\min }{V}_o\left(k\right)+\sigma \hfill \end{array}$$

(17)

where ${\mathcal{C}}_{\min }=\min [C_n=(1-{(1-{\mathcal{K}}_n{T}_0)}^2-{\displaystyle \frac{{\lambda }_n{T}_0}{2}}),n=1,2,3]>0$, ${\sum }_{n=1}^3{\tilde{o}}_n(T_0^2+2{\displaystyle \frac{{(1-{\mathcal{K}}_n{T}_0)}^2{T}_0}{{\lambda }_n}}{\varpi }_n^2\left(k\right))\le \sigma$, and $\sigma$ is a positive bounded constant.

If the above conditions are satisfied, we can conclude that ${\tilde{d}}_i\left(k\right)$ is bounded and the discrete-time disturbance observer can estimate the disturbance $d_i\left(k\right)$. □

4. Fractional-Order Sliding Mode Controller Based on the Fully Actuated System Approach

To complete the control goal, we design the fractional-order sliding mode controller based on the fully actuated system approach in this section.

4.1. Fully Actuated System Transition

We define the multi-spacecraft attitude system formation error and the attitude difference error for the ith spacecraft in the following form:

$$\begin{array}{c}\hfill \begin{array}{c}{e}_{yi}\left(k\right)=\sum _{j=1}^n{a}_{ij}\left({\mathcal{Y}}_i\left(k\right)-{\mathcal{Y}}_j\left(k\right)\right)+b_i\left({\mathcal{Y}}_i\left(k\right)-{\mathcal{Y}}_0\left(k\right)\right)\hfill \\ e_{xi}\left(k\right)=\sum _{j=1}^n{a}_{ij}\left({\mathcal{X}}_i\left(k\right)-{\mathcal{X}}_j\left(k\right)\right)+b_i({\mathcal{X}}_i\left(k\right)-{\mathcal{X}}_0\left(k\right))\hfill \end{array}\end{array}$$

(18)

Then, we define $e_y\left(k\right)={[e_{y1}^{\mathrm{T}}\left(k\right),e_{y2}^{\mathrm{T}}\left(k\right),\dots ,e_{yN}^{\mathrm{T}}\left(k\right)]}^{\mathrm{T}}$ and $e_x\left(k\right)={[e_{x1}^{\mathrm{T}}\left(k\right),e_{x2}^{\mathrm{T}}\left(k\right),\dots ,e_{xN}^{\mathrm{T}}\left(k\right)]}^{\mathrm{T}}$. Thus, the system (18) can be rewritten as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{e}_y\left(k\right)=(L+B)\otimes I_3\overline{\mathcal{Y}}\left(k\right)-b_{N\times 1}\otimes {\mathcal{Y}}_0\left(k\right)\hfill \\ e_x\left(k\right)=(L+B)\otimes I_3\overline{\mathcal{X}}\left(k\right)-b_{N\times 1}\otimes {\mathcal{X}}_0\left(k\right)\hfill \end{array}\end{array}$$

(19)

where $\overline{\mathcal{Y}}\left(k\right)={\left[{\mathcal{Y}}_1^{\mathrm{T}}\left(k\right),{\mathcal{Y}}_2^{\mathrm{T}}\left(k\right),\dots ,{\mathcal{Y}}_N^{\mathrm{T}}\left(k\right)\right]}^{\mathrm{T}}$ and $\overline{\mathcal{X}}\left(k\right)={\left[{\mathcal{X}}_1^{\mathrm{T}}\left(k\right),{\mathcal{X}}_2^{\mathrm{T}}\left(k\right),\dots ,{\mathcal{X}}_N^{\mathrm{T}}\left(k\right)\right]}^{\mathrm{T}}$, $b_{N\times 1}={\left[b_1,b_2,\dots ,b_N\right]}^{\mathrm{T}}$.

Combining the ith spacecraft attitude system (2) and (19), we have,

$$\begin{array}{cc}& e_y(k+1)=e_y\left(k\right)+T_0{e}_x\left(k\right)\hfill \\ & e_x(k+1)=e_x\left(k\right)+(L+B)\otimes I_3{T}_0\left(\overline{\Gamma }\overline{\mathcal{X}}\left(k\right)\right)+(L+B)\otimes I_3{T}_0(\overline{\mathcal{G}}\overline{u}\left(k\right)+\overline{d}\left(k\right))\hfill \\ & -T_0{b}_{N\times 1}\otimes {\alpha }_0\left(k\right)\hfill \end{array}$$

(20)

where $\overline{\Gamma }=\mathrm{diag}({\Gamma }_1,{\Gamma }_2,\dots ,{\Gamma }_N)\in {\Re }^{3N\times 3N}$, $\overline{\mathcal{G}}=\mathrm{diag}({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_N)\in {\Re }^{3N\times 3N}$, $\overline{u}\left(k\right)={[u_1^{\mathrm{T}}\left(k\right),u_2^{\mathrm{T}}\left(k\right),\dots ,u_N^{\mathrm{T}}\left(k\right)]}^{\mathrm{T}}\in {\Re }^{3N\times 1}$ and $\overline{d}\left(k\right)={[d_1^{\mathrm{T}}\left(k\right),d_2^{\mathrm{T}}\left(k\right),\dots ,d_N^{\mathrm{T}}\left(k\right)]}^{\mathrm{T}}\in {\Re }^{3N\times 1}$.

For facilitating subsequent controller design, we define $\mathcal{H}=(L+B)\otimes I_3$. Thus, $\mathcal{H}$ is a positive definite matrix through Assumption 3. Substituting (19) into (20), it can be deduced that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill e_y(k+1)=& e_y\left(k\right)+T_0{e}_x\left(k\right)\hfill \\ \hfill e_x(k+1)=& (I_{3N}+T_0\mathcal{H}\overline{\Gamma }{\mathcal{H}}^{-1})e_x\left(k\right)+T_0\mathcal{H}(\overline{\mathcal{G}}\overline{u}\left(k\right)+\overline{d}\left(k\right))-T_0{b}_{N\times 1}\otimes {\alpha }_0\left(k\right)\hfill \\ & +T_0\mathcal{H}\overline{\Gamma }{\mathcal{H}}^{-1}(b_{N\times 1}\otimes {\mathcal{X}}_0\left(k\right))\hfill \end{array}\end{array}$$

(21)

Because $\mathrm{rank}\left({\mathrm{T}}_0\mathcal{H}\overline{\mathcal{G}}\right)=3\mathrm{N}$, the multi-spacecraft formation attitude error system (21) is a fully actuated system from Definition 3. To simplify the subsequent expressions, the system is reformulated as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill e_y(k+1)=& f_1\left(e_y\left(k\right)\right)+g_1{e}_x\left(k\right),\hfill \\ \hfill e_x(k+1)=& f_2(e_y\left(k\right),e_x\left(k\right))+g_2(e_y\left(k\right),e_x\left(k\right))\overline{u}\left(k\right)+T_0\mathcal{H}\overline{d}\left(k\right)+\Theta \hfill \end{array}\end{array}$$

(22)

where $f_1\left(e_y\left(k\right)\right)=e_y\left(k\right)$, $g_1=T_0$, $f_2(e_y\left(k\right),e_x\left(k\right))=(I_{3N}+T_0\mathcal{H}\overline{\Gamma }{\mathcal{H}}^{-1})e_x\left(k\right)$, $g_2(e_y\left(k\right),e_x\left(k\right))=T_0\mathcal{H}\overline{\mathcal{G}}$, $\Theta =-T_0{b}_{N\times 1}\otimes {\alpha }_0\left(k\right)+T_0\mathcal{H}\overline{\Gamma }{\mathcal{H}}^{-1}(b_{N\times 1}\otimes {\mathcal{X}}_0\left(k\right))$.

Then, according to the discrete time fully actuated system approach, we define the coordinate transformation as

$$\begin{array}{c}\hfill \begin{array}{cc}& {\mathcal{Z}}_1\left(k\right)=e_y\left(k\right)\hfill \\ & {\mathcal{Z}}_2\left(k\right)=f_1\left(e_y\left(k\right)\right)+g_1{e}_x\left(k\right)\hfill \end{array}\end{array}$$

(23)

Then, it can be deduced that

$$\begin{array}{cc}\hfill {\mathcal{Z}}_2(k+1)& =e_y(k+1)+g_1{e}_x(k+1)\hfill \\ & =e_y(k+1)+g_1{f}_2(e_y\left(k\right),e_x\left(k\right))+g_1{g}_2(e_y\left(k\right),e_x\left(k\right))\overline{u}\left(k\right)\hfill \\ & +g_1{T}_0\mathcal{H}\overline{d}\left(k\right)+g_1\Theta \hfill \end{array}$$

(24)

From (23), we can obtain that

$$\begin{array}{c}\hfill \begin{array}{cc}& e_y\left(k\right)={\mathcal{Z}}_1\left(k\right)\hfill \\ & e_x\left(k\right)=g_1^{-1}\left[{\mathcal{Z}}_2\left(k\right)-{\mathcal{Z}}_1\left(k\right)\right]\hfill \end{array}\end{array}$$

(25)

Consequently, the original system (21) can be rewritten by ${\mathcal{Z}}_1\left(k\right)$ and ${\mathcal{Z}}_2\left(k\right)$ in the following step backward fully actuated form:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{Z}}_1(k+1)& ={\mathcal{Z}}_2\left(k\right)\hfill \\ \hfill {\mathcal{Z}}_2(k+1)& ={\mathcal{Z}}_2\left(k\right)+g_1{f}_2^{\prime }({\mathcal{Z}}_1\left(k\right),{\mathcal{Z}}_2\left(k\right))+g_1\Theta \hfill \\ & +g_1{g}_2^{\prime }({\mathcal{Z}}_1\left(k\right),{\mathcal{Z}}_2\left(k\right))\overline{u}\left(k\right)+g_1{T}_0\mathcal{H}\overline{d}\left(k\right)\hfill \end{array}\end{array}$$

(26)

where $f_2^{\prime }({\mathcal{Z}}_1\left(k\right),{\mathcal{Z}}_2\left(k\right))=f_2(e_y\left(k\right),e_x\left(k\right))$ and $g_2^{\prime }({\mathcal{Z}}_1\left(k\right),{\mathcal{Z}}_2\left(k\right))=g_2(e_y\left(k\right),e_x\left(k\right))$.

By using the discrete-time fully actuated system approach [15], we design the controller in the following form:

$$\begin{array}{c}\hfill \begin{array}{cc}& \overline{u}\left(k\right)=-{\left(g_1{g}_2^{\prime }({\mathcal{Z}}_1\left(k\right),{\mathcal{Z}}_2\left(k\right))\right)}^{-1}({\mathcal{Z}}_2\left(k\right)-q\left(k\right)\hfill \\ & + g_1{f}_2^{\prime }({\mathcal{Z}}_1\left(k\right),{\mathcal{Z}}_2\left(k\right)))\hfill \\ & q\left(k\right)={\Psi }_1{\mathcal{Z}}_1\left(k\right)+{\Psi }_2{\mathcal{Z}}_2\left(k\right)+l\left(k\right)-g_1\Theta \hfill \end{array}\end{array}$$

(27)

where $l\left(k\right)$ is the designed sliding mode controller in the subsequent part, ${\Psi }_1$ and ${\Psi }_2$ are the selected matrices through the fully actuated system approach.

Through the discrete-time fully actuated system approach, the discrete-time attitude formation system (21) can convert the following system:

$$\begin{array}{cc}& {\mathcal{Z}}_1(k+1)={\mathcal{Z}}_2\left(k\right)\hfill \\ & {\mathcal{Z}}_2(k+1)={\Psi }_1{\mathcal{Z}}_1\left(k\right)+{\Psi }_2{\mathcal{Z}}_2\left(k\right)+l\left(k\right)+g_1{T}_0\mathcal{H}\overline{d}\left(k\right)\hfill \end{array}$$

(28)

Remark 2.

${\Psi }_1$ and ${\Psi }_2\in {\Re }^{3N\times 3N}$ are constant matrices, and their design criteria are in the following form: Firstly, choose a Hurwitz matrix $\overline{\Omega }\in {\Re }^{6N\times 6N}$ and a matrix $\Phi \in {\Re }^{3N\times 6N}$. Then, we define $V(\overline{\Omega },\Phi )=\left[\begin{array}{c}\overline{\Omega }\\ \overline{\Omega }\Phi \end{array}\right]\in {\Re }^{6N\times 6N}$. It can obtain that $\left[{\Psi }_1,{\Psi }_2\right]=\Phi {\overline{\Omega }}^2{V}^{-1}(\overline{\Omega },\Phi )$ according to the fully actuated system approach [39].

Remark 3.

The discrete-time fully actuated system approach allows us to configure the matrices $[{\Psi }_1,{\Psi }_2]$ in the controller (27), which guarantees that the transformed system possesses the desired closed-loop properties. This approach enables the controller designed in the subsequent part to have improved flexibility and robustness. Therefore, $l\left(k\right)$ will be constructed on the basis of the transformed system.

4.2. Fractional-Order Sliding Mode Controller Design and Stability Analysis

In this subsection, a discrete-time fractional-order sliding mode controller will be adopted to ensure that the attitude formation error can be bounded.

Choose the fractional-order sliding mode as:

$$\begin{array}{c}\hfill \mathcal{S}\left(k\right)={\mathcal{Q}}_1{\nabla }^{{\gamma }_2-1}{\mathcal{Z}}_1\left(k\right)+{\mathcal{Z}}_2\left(k\right)\end{array}$$

(29)

where ${\mathcal{Q}}_1\in {\Re }^{3N\times 3N}$ is a designed positive diagonal matrix, abd ${\gamma }_2$ is the fractional-order parameter.

From (28) and (29), we design the sliding mode controller in the following form:

$$\begin{array}{cc}\hfill l\left(k\right)=& -{\mathcal{Q}}_1{\nabla }^{{\gamma }_2}{\mathcal{Z}}_2\left(k\right)-{\Psi }_1{\mathcal{Z}}_1\left(k\right)-({\Psi }_2-I_{3N}){\mathcal{Z}}_2\left(k\right)\hfill \\ & -g_1{T}_0\mathcal{H}\overline{\widehat{d}}\left(k\right)-q_1{T}_0\mathcal{S}\left(k\right)-q_2{T}_0\mathrm{sgn}\left[\mathcal{S}\left(k\right)\right]\hfill \end{array}$$

(30)

where $\overline{\widehat{d}}\left(k\right)={[{\widehat{d}}_1^{\mathrm{T}}\left(k\right),{\widehat{d}}_2^{\mathrm{T}}\left(k\right),\dots ,{\widehat{d}}_N^{\mathrm{T}}\left(k\right)]}^{\mathrm{T}}$, $q_1\in {\Re }^{3N\times 3N}$ and $q_2\in {\Re }^{3N\times 3N}$ are the positive diagonal matrices, and $\mathrm{sgn}\left[·\right]$ is the sign function.

Theorem 2.

For the spacecraft attitude error formation system (28), if ${\left(I_{3N}-q_1\right)}^{\mathrm{T}}{q}_2$ and ${\left(2I_{3N}-q_1\right)}^{\mathrm{T}}{q}_1$ are positive definite matrices, by the fully actuated approach controller (27), the discrete-time fractional-order sliding mode controller (30), and the observer (9). The formation attitude error can be bounded, and every spacecraft can track the virtual leader attitude signal.

Proof. 

According to Lemma 1 and (29), we can know

$$\begin{array}{cc}\hfill \mathcal{S}(k+1)-\mathcal{S}\left(k\right)& ={\mathcal{Q}}_1{\nabla }^{{\gamma }_2-1}\left({\mathcal{Z}}_1(k+1)-{\mathcal{Z}}_1\left(k\right)\right)+\left({\mathcal{Z}}_2(k+1)-{\mathcal{Z}}_2\left(k\right)\right)\hfill \\ & ={\mathcal{Q}}_1{\nabla }^{{\gamma }_2-1}{\nabla }^1{\mathcal{Z}}_1(k+1)+({\mathcal{Z}}_2(k+1)-{\mathcal{Z}}_2\left(k\right))\hfill \\ & ={\mathcal{Q}}_1{\nabla }^{{\gamma }_2}{\mathcal{Z}}_1(k+1)+({\mathcal{Z}}_2(k+1)-{\mathcal{Z}}_2\left(k\right))\hfill \end{array}$$

(31)

From (28) and (30), we can obtain that

$$\begin{array}{cc}\hfill \mathcal{S}(k+1)-\mathcal{S}\left(k\right)& ={\mathcal{Q}}_1{\nabla }^{{\gamma }_2}{\mathcal{Z}}_2\left(k\right)+[{\Psi }_1{\mathcal{Z}}_1\left(k\right)+\left({\Psi }_2-I_{3N}\right){\mathcal{Z}}_2\left(k\right)+l\left(k\right)+g_1{T}_0\mathcal{H}\overline{d}\left(k\right)]\hfill \\ & ={\mathcal{Q}}_1{\nabla }^{{\gamma }_2}{\mathcal{Z}}_2\left(k\right)+[-{\mathcal{Q}}_1{\nabla }^{{\gamma }_2}{\mathcal{Z}}_2\left(k\right)+g_1{T}_0\mathcal{H}\overline{\tilde{d}}\left(k\right)-q_1{T}_{0}S\left(k\right)\hfill \\ & - q_2{T}_{0}sgn\left[\mathcal{S}\left(k\right)\right]]\hfill \\ & =g_1{T}_0\mathcal{H}\overline{\tilde{d}}\left(k\right)-q_1{T}_0\mathcal{S}\left(k\right)-q_2{T}_{0}sgn\left[\mathcal{S}\left(k\right)\right]\hfill \end{array}$$

(32)

where $\overline{\tilde{d}}\left(k\right)={[{\tilde{d}}_1^{\mathrm{T}}\left(k\right),{\tilde{d}}_2^{\mathrm{T}}\left(k\right),\dots ,{\tilde{d}}_N^{\mathrm{T}}\left(k\right)]}^{\mathrm{T}}$.

Then, we choose the Lyapunov function in the following form:

$$V_s\left(k\right)={\displaystyle \frac{1}{T_0^2}}{\mathcal{S}}^T\left(k\right)\mathcal{S}\left(k\right)$$

(33)

Thus, the first difference is calculated as

$$\begin{array}{cc}\hfill \Delta V_s\left(k\right)& ={\displaystyle \frac{1}{T_0^2}}{\mathcal{S}}^T(k+1)\mathcal{S}(k+1)-{\displaystyle \frac{1}{T_0^2}}{\mathcal{S}}^T\left(k\right)\mathcal{S}\left(k\right)\hfill \\ & ={\displaystyle \frac{1}{T_0^2}}{\left(\mathcal{S}(k+1)+\mathcal{S}\left(k\right)\right)}^{\mathrm{T}}\left(\mathcal{S}(k+1)-\mathcal{S}\left(k\right)\right)\hfill \end{array}$$

(34)

Substituting (32) into (34), we have

$$\begin{array}{cc}\hfill \Delta V_s\left(k\right)& ={\left(g_1\mathcal{H}\overline{\tilde{d}}\left(k\right)+\left(2I_{3N}-q_1\right)\mathcal{S}\left(k\right)-q_2\mathrm{sgn}\left[\mathcal{S}\left(k\right)\right]\right)}^{\mathrm{T}}\hfill \\ & \left(g_1\mathcal{H}\overline{\tilde{d}}\left(k\right)-q_1\mathcal{S}\left(k\right)-q_2\mathrm{sgn}\left[\mathcal{S}\left(k\right)\right]\right)\hfill \\ & =- {\mathcal{S}}^{\mathrm{T}}\left(k\right){\left(2I_{3N}-q_1\right)}^{\mathrm{T}}{q}_{1}S\left(k\right)+g_1^2{\overline{\tilde{d}}}^{\mathrm{T}}\left(k\right){\mathcal{H}}^{\mathrm{T}}\mathcal{H}\overline{\tilde{d}}\left(k\right)\hfill \\ & + 2g_1{\mathcal{S}}^{\mathrm{T}}\left(k\right)\left[{\left(I_{3N}-q_1\right)}^{\mathrm{T}}\mathcal{H}\right]\overline{\tilde{d}}\left(k\right)-2{\mathcal{S}}^{\mathrm{T}}\left(k\right)\left[{\left(I_{3N}-q_1\right)}^{\mathrm{T}}{q}_2\right]\mathrm{sgn}\left[\mathcal{S}\left(k\right)\right]\hfill \\ & - 2g_1{\overline{\tilde{d}}}^{\mathrm{T}}\left(k\right){\mathcal{H}}^{\mathrm{T}}{q}_{2}sgn\left[\mathcal{S}\left(k\right)\right]+sgn{\left[\mathcal{S}\left(k\right)\right]}^{\mathrm{T}}{q}_2^{\mathrm{T}}{q}_{2}sgn\left[\mathcal{S}\left(k\right)\right]\hfill \end{array}$$

(35)

Because ${(I_{3N}-q_1)}^{\mathrm{T}}{q}_2$ and $q_2$ are known positive definite matrices, we can easily derive the following inequalities based on the properties of the sign function.

$$\begin{array}{c}\hfill -2{\mathcal{S}}^{\mathrm{T}}\left(k\right)\left[{\left(I_{3N}-q_1\right)}^{\mathrm{T}}{q}_2\right]\mathrm{sgn}\left[\mathcal{S}\left(k\right)\right]\le 0\end{array}$$

(36)

$$\begin{array}{c}\hfill \mathrm{sgn}{\left[\mathcal{S}\left(k\right)\right]}^{\mathrm{T}}{q}_2^{\mathrm{T}}{q}_2\mathrm{sgn}\left[\mathcal{S}\left(k\right)\right]\le {\tau }_1\end{array}$$

(37)

where ${\tau }_1$ is a positive bounded constant.

Additionally, according to Theorem 1, we know

$$-2g_1{\overline{\tilde{d}}}^{\mathrm{T}}\left(k\right){\mathcal{H}}^{\mathrm{T}}{q}_{2}sgn\left[\mathcal{S}\left(k\right)\right]\le {\xi }_1$$

(38)

where ${\xi }_1$ is a positive bounded constant.

Moreover, from Young’s inequality, it can be deduced that

$$\begin{array}{cc}\hfill 2g_1{\mathcal{S}}^{\mathrm{T}}\left(k\right)\left[{\left(I_{3N}-q_1\right)}^{\mathrm{T}}\mathcal{H}\right]\overline{\tilde{d}}\left(k\right)& \le 2g_1{\lambda }_{max}\left(\left[{\left(I_{3N}-q_1\right)}^{\mathrm{T}}\mathcal{H}\right]\right)\left|\right|{\mathcal{S}}^{\mathrm{T}}\left(k\right){\left|\right|}_2\left|\right|\tilde{d}\left(k\right){\left|\right|}_2\hfill \\ & \le g_1{\lambda }_{\max }\left({\left(I_{3N}-q_1\right)}^{\mathrm{T}}\mathcal{H})\right)[{\displaystyle \frac{{\lambda }_{\min }\left(0.5{\left(2I_{3N}-q_1\right)}^{\mathrm{T}}{q}_1\right)}{g_1{\lambda }_{\max }\left(\left[{\left(I_{3N}-q_1\right)}^{\mathrm{T}}\mathcal{H}\right]\right)}}\hfill \\ & {\mathcal{S}}^{\mathrm{T}}\left(k\right)\mathcal{S}\left(k\right)+{\displaystyle \frac{g_1{\lambda }_{\max }\left(\left[{\left(I_{3N}-q_1\right)}^{\mathrm{T}}\mathcal{H}\right]\right)}{{\lambda }_{\min }\left(0.5{\left(2I_{3N}-q_1\right)}^{\mathrm{T}}{q}_1\right)}}{\overline{\tilde{d}}}^{\mathrm{T}}\left(k\right)\overline{\tilde{d}}\left(k\right)]\hfill \end{array}$$

(39)

where ${\lambda }_{\min }\left(·\right)$ denotes the minimum eigenvalue of the matrix, ${\lambda }_{\max }\left(·\right)$ denotes the maximum eigenvalue of the matrix, ${\left|\right|·\left|\right|}_2$ denotes the 2-norm.

Therefore, (35) can be written as:

$$\begin{array}{cc}\hfill \Delta V_s\left(k\right)& \le -{\mathcal{S}}^{\mathrm{T}}\left(k\right){\left(2I_{3N}-q_1\right)}^{\mathrm{T}}{q}_1\mathcal{S}\left(k\right)+{\lambda }_{min}\left(0.5{\left(2I_{3N}-q_1\right)}^{\mathrm{T}}{q}_1\right){\mathcal{S}}^{\mathrm{T}}\left(k\right)\mathcal{S}\left(k\right)\hfill \\ & +{\tau }_1+{\xi }_1+{\displaystyle \frac{g_1^2{\lambda }_{\max }^2\left(\left[{\left(I_{3N}-q_1\right)}^{\mathrm{T}}\mathcal{H}\right]\right)}{{\lambda }_{\min }\left(0.5{\left(2I_{3N}-q_1\right)}^{\mathrm{T}}{q}_1\right)}}{\overline{\tilde{d}}}^{\mathrm{T}}\left(k\right)\overline{\tilde{d}}\left(k\right)+g_1^2{\overline{\tilde{d}}}^{\mathrm{T}}\left(k\right){\mathcal{H}}^{\mathrm{T}}\mathcal{H}\overline{\tilde{d}}\left(k\right)\hfill \\ & \le -{\lambda }_{min}\left(0.5{\left(2I_{3N}-q_1\right)}^{\mathrm{T}}{q}_1\right){\mathcal{S}}^{\mathrm{T}}\left(k\right)\mathcal{S}\left(k\right)+{\displaystyle \frac{g_1^2{\lambda }_{\max }^2\left(\left[{\left(I_{3N}-q_1\right)}^{\mathrm{T}}\mathcal{H}\right]\right)}{{\lambda }_{\min }\left(0.5{\left(2I_{3N}-q_1\right)}^{\mathrm{T}}{q}_1\right)}}{\overline{\tilde{d}}}^{\mathrm{T}}\left(k\right)\overline{\tilde{d}}\left(k\right)\hfill \\ & +{\tau }_1+{\xi }_1+g_1^2{\overline{\tilde{d}}}^{\mathrm{T}}\left(k\right){\mathcal{H}}^{\mathrm{T}}\mathcal{H}\overline{\tilde{d}}\left(k\right)\hfill \\ & \le -{\kappa }_1{V}_s\left(k\right)+{\kappa }_2\hfill \end{array}$$

(40)

where ${\kappa }_1=T_0^2{\lambda }_{\min }\left(0.5{\left(2I_{3N}-q_1\right)}^{\mathrm{T}}{q}_1\right)>0$, ${\kappa }_2={\tau }_1+{\xi }_1+{\displaystyle \frac{g_1^2{\lambda }_{\max }^2\left(\left[{\left(I_{3N}-q_1\right)}^{\mathrm{T}}\mathcal{H}\right]\right)}{{\lambda }_{\min }\left(0.5{\left(2I_{3N}-q_1\right)}^{\mathrm{T}}{q}_1\right)}}{\overline{\tilde{d}}}^{\mathrm{T}}\left(k\right)\overline{\tilde{d}}\left(k\right)+g_1^2{\overline{\tilde{d}}}^{\mathrm{T}}\left(k\right){\mathcal{H}}^{\mathrm{T}}\mathcal{H}\overline{\tilde{d}}\left(k\right)$, and ${\kappa }_2$ is a positive bounded value.

Above all, we can obtain that the formation attitude error can be bounded to zero. Additionally, every spacecraft can track the virtual leader’s attitude. □

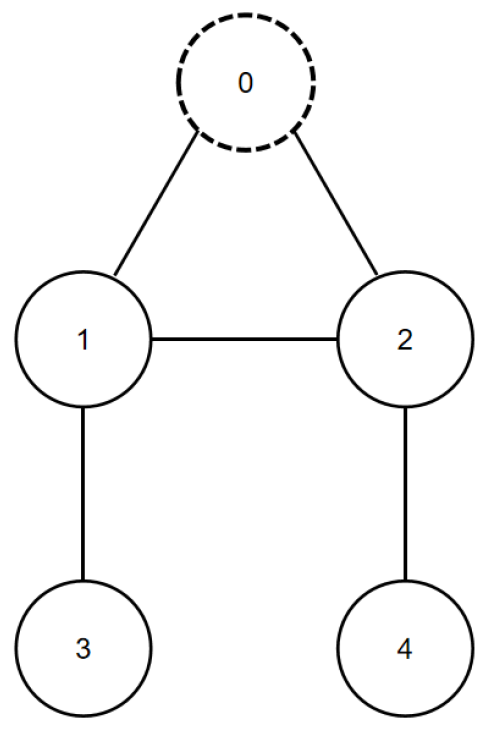
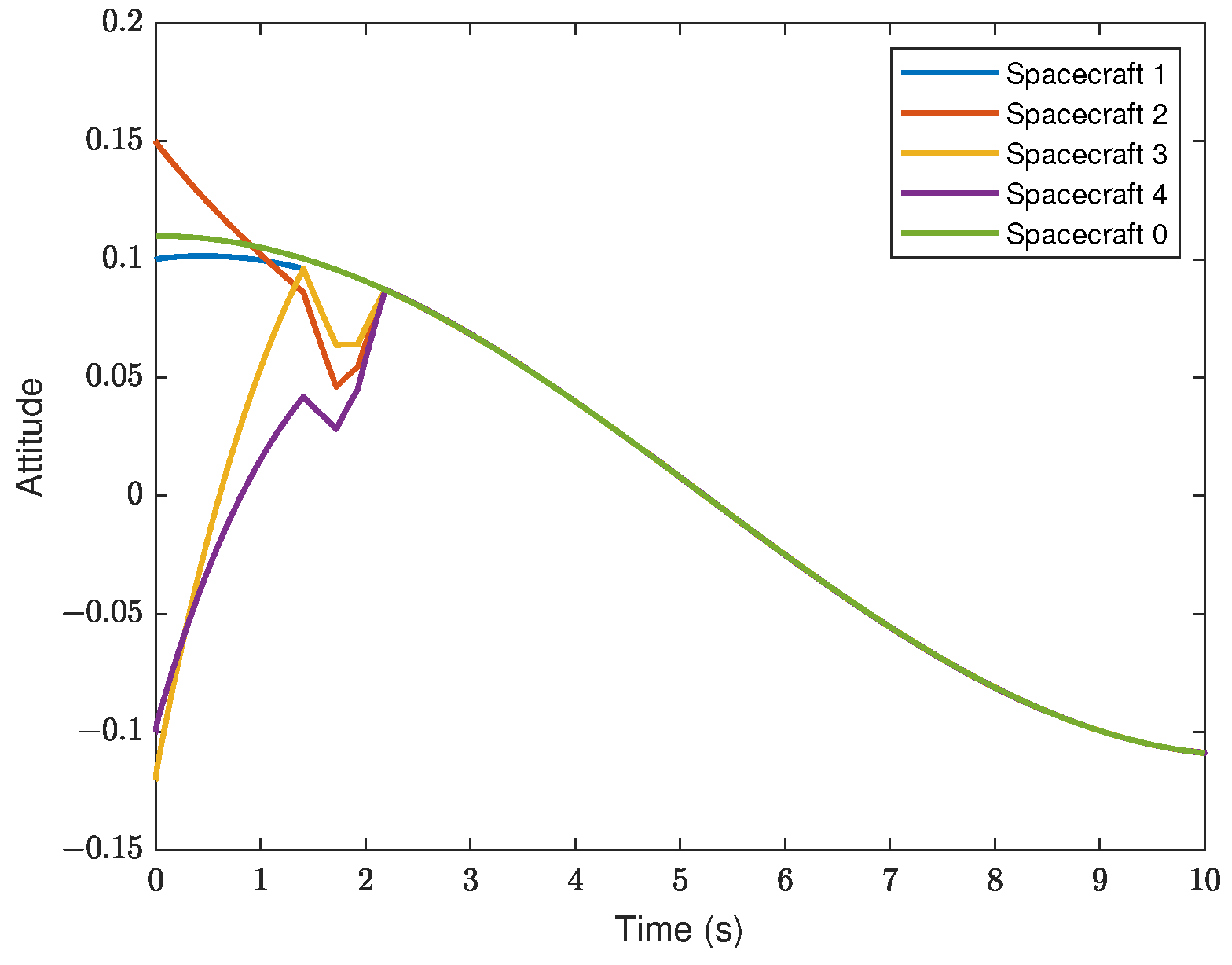
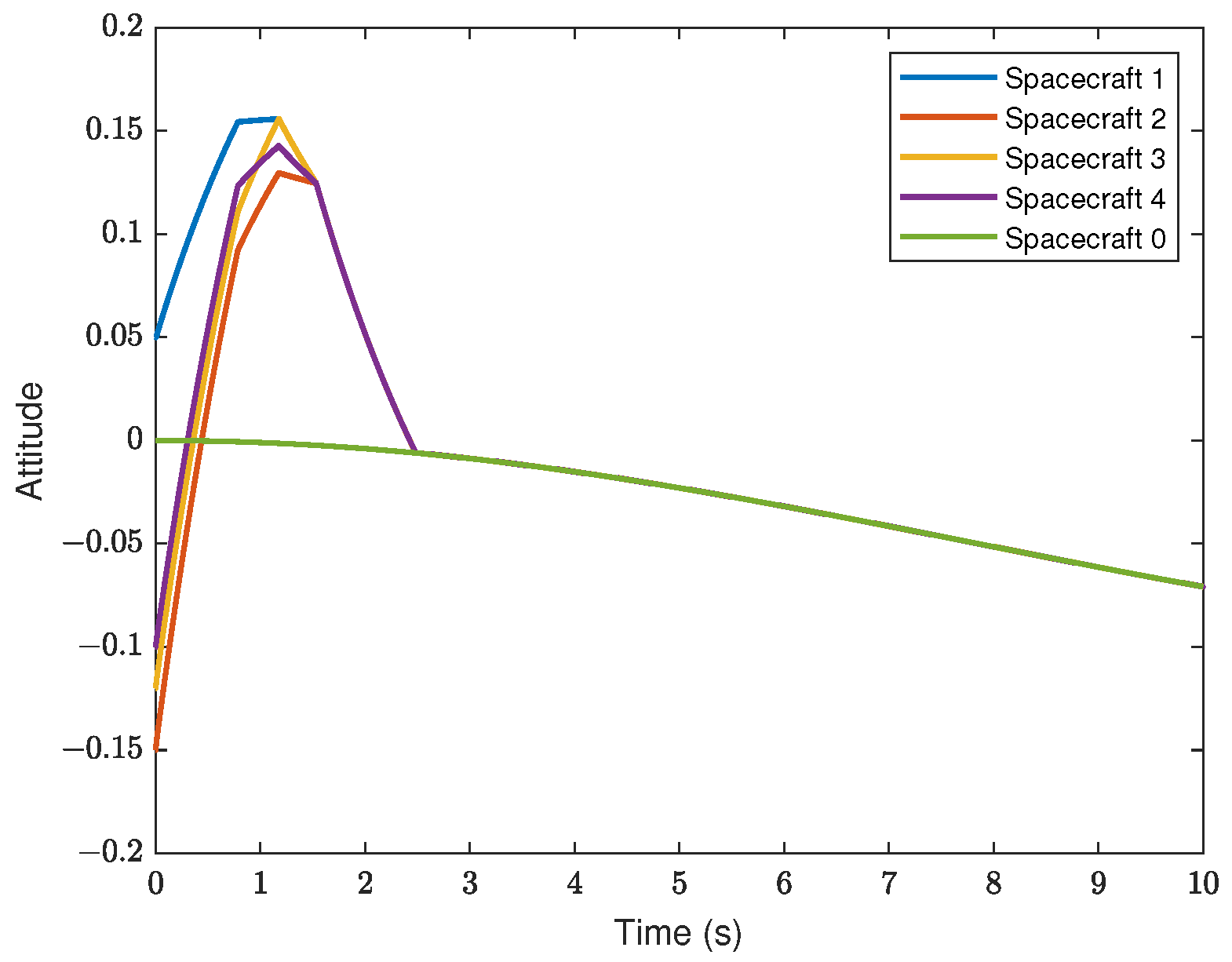
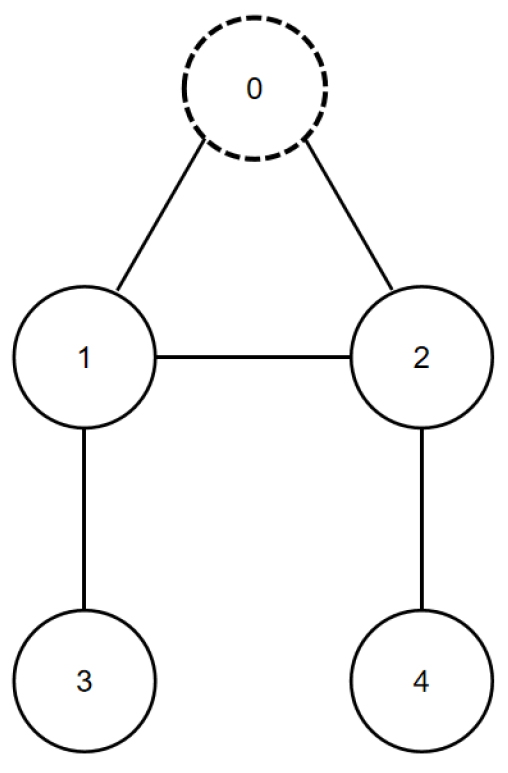
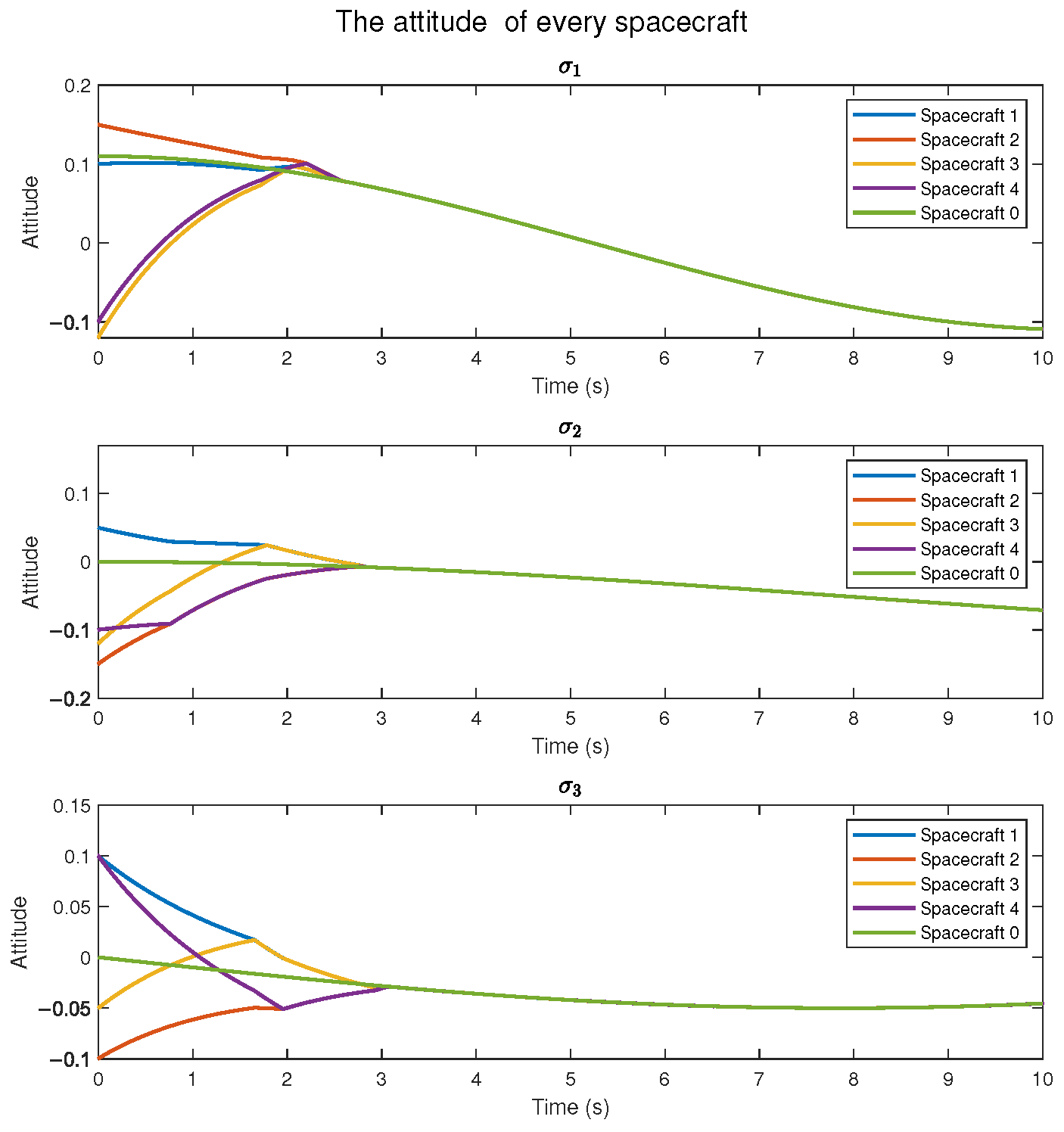
5. Simulation Results

To verify the effectiveness of the designed observer and controller, there are some simulation results. Set the parameters of ${\mathcal{M}}_i$ as

$${\mathcal{M}}_i=\left[\begin{array}{ccc}20& 1.2& 0.9\\ 1.2& 17& 1.4\\ 0.9& 1.4& 15\end{array}\right]\mathrm{kg}·{\mathrm{m}}^2$$

In this simulation, the communication topology of the multi-spacecraft system is presented in Figure 3.

The initial states of every spacecraft are chosen as

$$\begin{array}{cc}\hfill & {\mathcal{Y}}_1\left(0\right)={\left[\begin{array}{c}0.1,0.05,0.1\end{array}\right]}^{\mathrm{T}}{\mathcal{X}}_1\left(0\right)={\left[\begin{array}{c}0.004,-0.003,0.005\end{array}\right]}^{\mathrm{T}}\hfill \\ & {\mathcal{Y}}_2\left(0\right)={\left[\begin{array}{c}0.15,-0.15,-0.1\end{array}\right]}^{\mathrm{T}}{\mathcal{X}}_2\left(0\right)={\left[\begin{array}{c}0.004,-0.005,0.007\end{array}\right]}^{\mathrm{T}}\hfill \\ & {\mathcal{Y}}_3\left(0\right)={\left[\begin{array}{c}-0.12,-0.12,-0.05\end{array}\right]}^{\mathrm{T}}{\mathcal{X}}_3\left(0\right)={\left[\begin{array}{c}0.005,0.005,0.005\end{array}\right]}^{\mathrm{T}}\hfill \\ & {\mathcal{Y}}_4\left(0\right)={\left[\begin{array}{c}-0.1,-0.1,0.1\end{array}\right]}^{\mathrm{T}}{\mathcal{X}}_4\left(0\right)={\left[\begin{array}{c}-0.003,-0.009,0.006\end{array}\right]}^{\mathrm{T}}\hfill \end{array}$$

The discrete-time virtual leader signal is derived from the following associated signal:

$${\mathcal{Y}}_0\left(t\right)=\left[\begin{array}{c}0.11cos\left(0.3t\right)\\ 0.05cos\left(0.2t\right)-0.05\\ -0.05sin\left(0.2t\right)\end{array}\right]$$

The discrete-time disturbance $d\left(k\right)$ is derived from the following associated disturbance:

$$d\left(t\right)=\left[\begin{array}{c}2-1sin\left(0.3t\right)\\ 4cos\left(0.1t\right)-5sin\left(0.25t\right)\\ 1cos\left(0.4t\right)-1\end{array}\right]\times {10}^{-3} \mathrm{N}·\mathrm{m}$$

Then, the parameters of the observer are chosen as $\lambda =0.01I_3$, $\mathcal{K}=\mathrm{diag}[20,16,16]$, ${\gamma }_1=0.5$ and ${\gamma }_2=0.55$, the parameters of the controller are chosen as ${\psi }_1=-0.351I_{12}$, ${\psi }_2=-0.165I_{12}$, ${\mathcal{Q}}_1=0.005I_{12}$, $q_1=0.1I_{12}$, and $q_2=0.1I_{12}$. Additionally, the discrete sample time is $T_0=0.001 \mathrm{s}$.

Based on the parameters above, Figure 4, Figure 5, Figure 6 and Figure 7 show the simulation results. In Figure 4, the discrete-time disturbance observer enables accurate estimation of disturbance $d\left(k\right)$ while the estimation errors are bounded. Moreover, Figure 5, Figure 6 and Figure 7 present the attitude tracking results for the virtual leader and the followers. As shown in Figure 8, Figure 9, Figure 10 and Figure 11, the attitude error between each spacecraft and the virtual leader demonstrates that the proposed controller enables all spacecraft not only to achieve but also to maintain attitude consensus with the virtual leader (where ${\sigma }_{\mathrm{e},\mathrm{i}}$ denotes the attitude error between the spacecraft and spacecraft 0 for the ith dimension). The simulation results validate that the discrete-time fractional-order sliding mode control method proposed in this paper can effectively achieve cooperative control for a multi-spacecraft system.

To assess the proposed controller, there are some simulations to compare the control performance with other controllers. As shown in Figure 12 and

Table 1. Controller performance comparison.

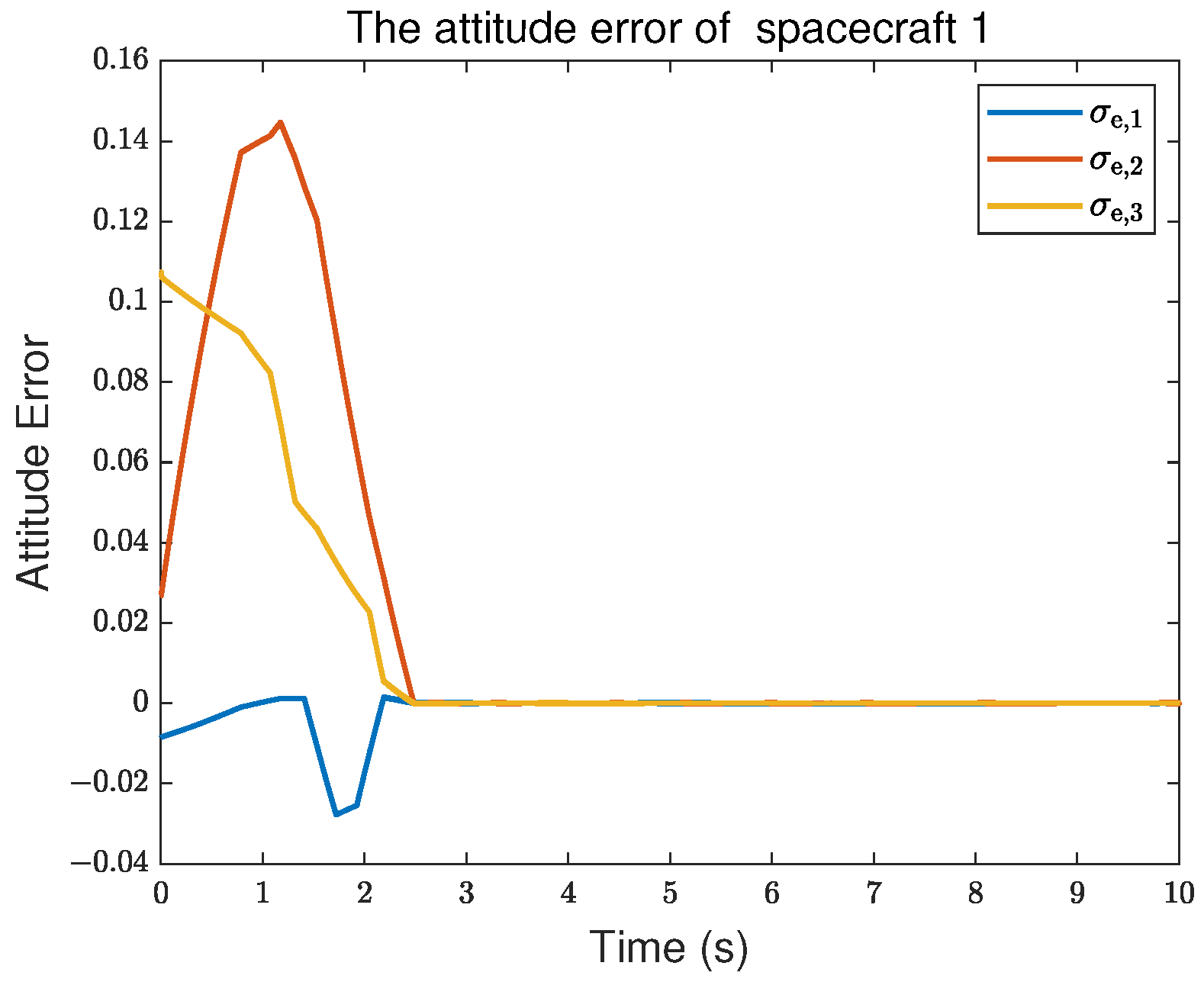
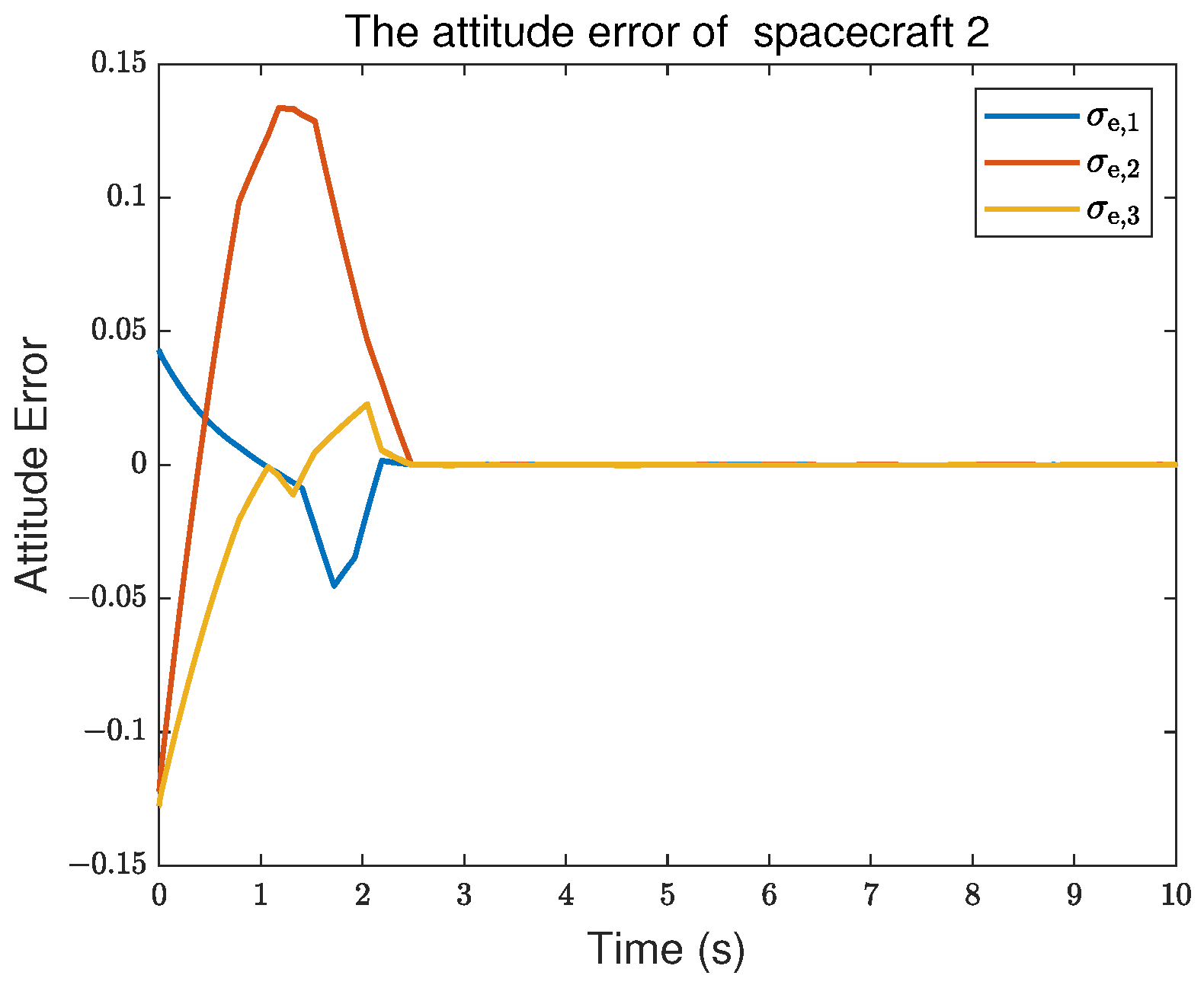
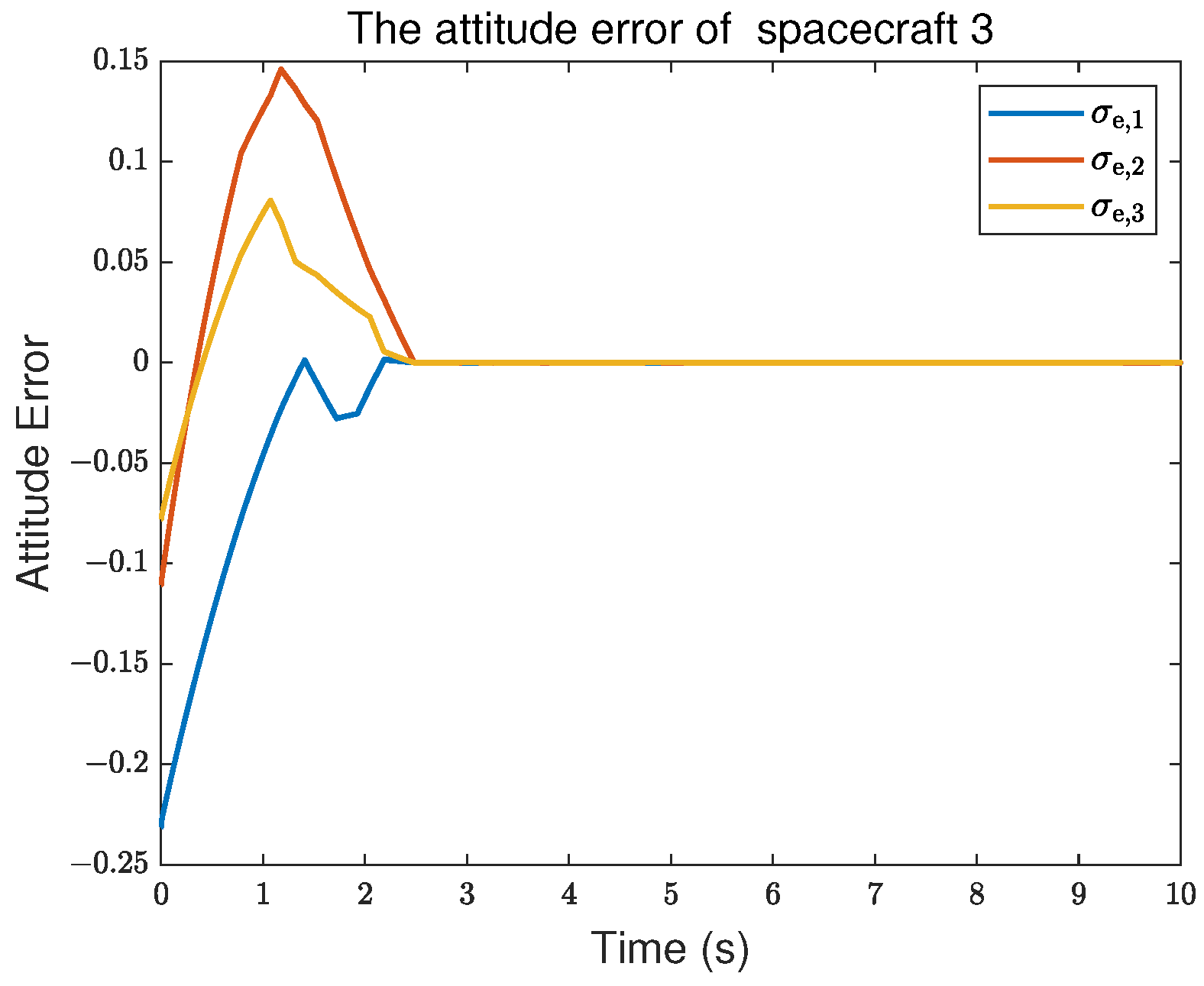
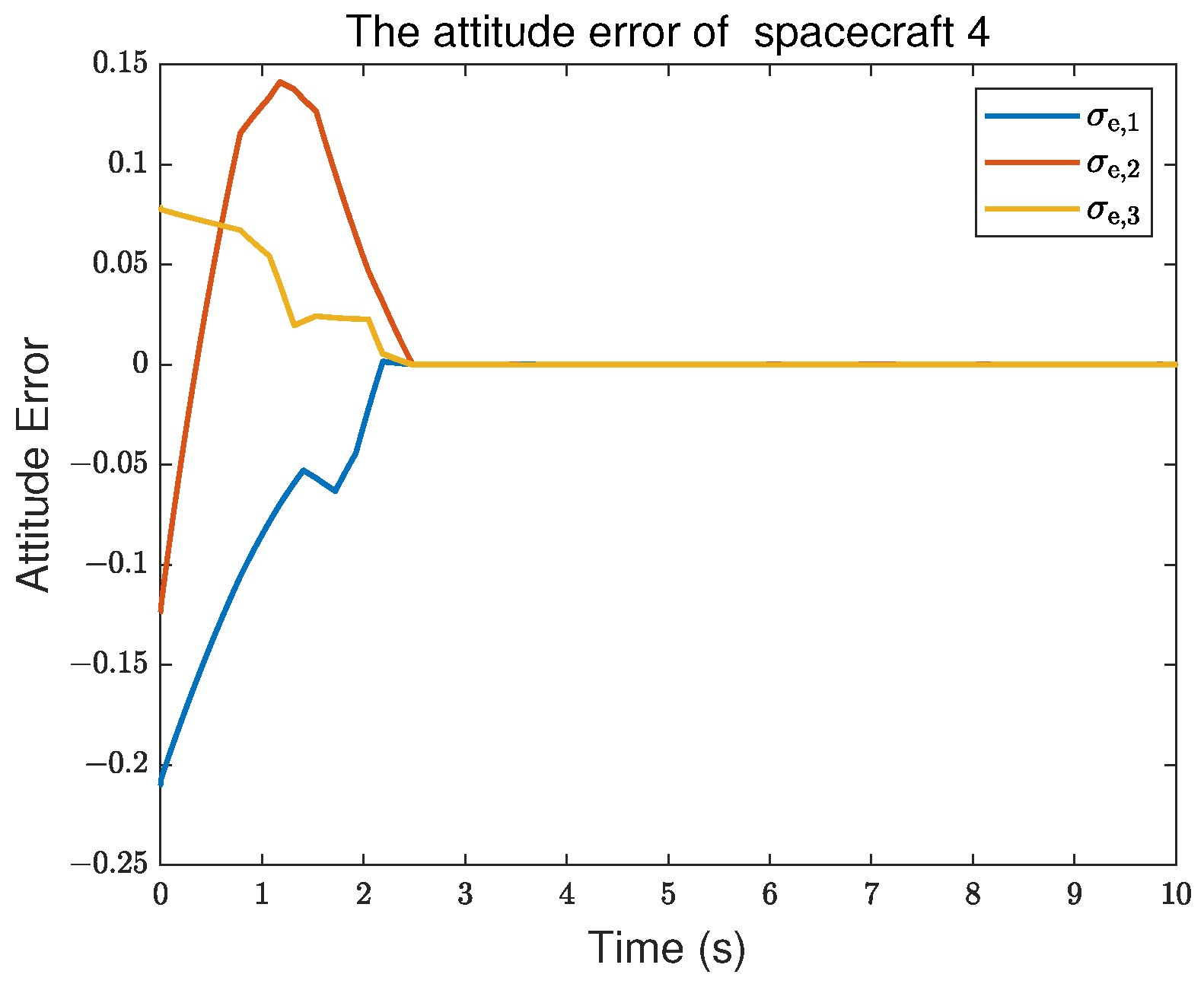
Controller Type	Maximum Overshoot	Settling Time	Square Error
Proposed controller	0.14	<3 s	36.9631
Integer-order sliding mode controller	0.25	<5 s	145.9648
Fractional-order backstepping controller	No Overshoot	<7 s	12.3702

Maximum Overshoot: Maximum attitude error when overshoot exists, calculated as $max|{\sigma }_{\mathrm{e},\mathrm{i}}|$ where $i=1,2,3$. Settling Time: Maximum settling time for $i=1,2,3$. Square Error: Sum of squared error over simulation period, calculated as ${\sum }_{k=0}^{10/T_0}\left({\sigma }_{\mathrm{e},\mathrm{l}}^2\left(k\right)+{\sigma }_{\mathrm{e},2}^2\left(k\right)+{\sigma }_{\mathrm{e},3}^2\left(k\right)\right)$.

, under identical conditions, the fractional-order controller proposed in this paper exhibits faster setting time and reduced overshoot when compared to the integer-order controller. Furthermore, it shows improved attitude square error over the simulation period, indicating a clear advantage in fractional-order control. Compared with other fractional-order control method, the proposed approach still maintains a favorable setting time and high control accuracy. Nevertheless, it shows relatively poorer performance in the square error and overshoot.

To assess the controller parameter tuning sensitivity and applicability under various communication topologies, some simulations have been added. Figure 13 shows the new communication topology, and the parameters are set as $\lambda =0.005I_3$, $\mathcal{K}=\mathrm{diag}[50,36,36]$, ${\gamma }_1=0.55$, ${\gamma }_2=0.35$, ${\mathcal{Q}}_1=0.002I_{12}$, $q_1=0.15I_{12}$, and $q_2=0.05I_{12}$. In this situation, the attitude tracking of every spacecraft is shown in Figure 14. From Figure 14, we see that the proposed controller still enables each spacecraft to achieve attitude consensus. Moreover, it demonstrates applicability under various communication topologies and exhibits relatively low tuning sensitivity with respect to the relevant parameters that satisfy the design conditions.

6. Conclusions

In this paper, a discrete-time fractional-order sliding mode controller based on the fully actuated system approach has been proposed for the multi-spacecraft attitude tracking problem. This controller can enable every spacecraft to track the virtual leader’s attitude. To compensate for the disturbances, a discrete-time observer based on the fractional-order theory has been designed. This observer can ensure estimation errors are bounded. Finally, simulations are provided to show that the designed controller in this paper can make every spacecraft track the virtual leader’s attitude quickly under disturbances. Future work will involve extending the controller to a multi-spacecraft system with uncertain inertia matrices and communication delays, as well as further developing the optimization-based framework to enhance control performance.