Analysis of Noise on Ordinary and Fractional-Order Financial Systems

Abstract

This study investigated the influence of stochastic fluctuations on financial system stability by analyzing both ordinary and fractional-order financial models under noise. The ordinary financial system experiences perturbations due to bounded random disturbances, whereas the fractional-order counterpart models memory-dependent behaviors by incorporating fractional Gaussian noise (FGN) characterized by a Hurst parameter that governs long-term correlations. This study used data generated through MATLAB simulations based on standard financial models from the literature. Numerical simulations compared system behavior in deterministic and noisy environments. The results reveal that ordinary systems experience transient fluctuations, quickly returning to a stable state, whereas fractional systems exhibit persistent deviations due to historical dependencies. This highlights the fundamental difference between integer-order and fractional-order derivatives in financial modeling. Our key findings indicate that noise significantly impacts interest rates, investment needs, price indices, and profit margins, with the fractional system displaying higher sensitivity to external shocks. These insights emphasize the necessity of incorporating memory effects in financial modeling to improve accuracy in predicting market behavior. The study further underscores the importance of adaptive monetary policies and risk management strategies to mitigate financial instability. Future research should explore hybrid models combining short-term stability with long-term memory effects for enhanced financial forecasting and stability analysis.

1. Introduction

Financial systems are inherently complex and subject to continuous interaction with various external influences, including monetary policies, market dynamics, investor sentiment, and unpredictable shocks [1,2]. Traditional economic models often adopt a deterministic framework, assuming linear relationships and stable trajectories [3]. However, real-world markets frequently display nonlinear, chaotic, and memory-dependent behavior, which makes them highly sensitive to both internal and external perturbations [4].

Recent studies highlight the crucial influence of stochastic fluctuations on the evolution of financial systems. Even small, bounded random perturbations can significantly alter patterns of investment, consumer activity, and overall market stability [1,2]. Accounting for noise within financial modeling frameworks enables a more authentic depiction of market volatility, crisis transmission, and structural uncertainty, thereby narrowing the gap between theoretical constructs and real-world economic behavior.

This study explored the impact of stochastic perturbations on both classical and fractional-order financial systems. The classical framework models the evolution of major macroeconomic indicators—such as interest rates, investment demand, and profit margins—through a system of nonlinear differential equations. To incorporate the long-term memory effects frequently observed in financial markets, the model is extended to a fractional-order formulation by employing Caputo fractional derivatives [5,6].

To account for real-world uncertainty, we introduced bounded Gaussian noise into the ordinary system and fractional Gaussian noise (fGn) into the fractional model [7]. These disturbances were modeled as external inputs affecting each equation in the system. Using numerical simulations, we analyzed the dynamic behavior under both deterministic and noisy conditions, evaluating the effect of noise intensity on system stability, predictability, and economic performance indicators [8].

By comparing the two modeling approaches, this research highlights how memory and stochasticity influence financial system behavior. The findings contribute to the growing field of stochastic financial modeling and provide insights relevant to economic forecasting, policy design, and risk management [9,10,11].

In light of the growing volatility in global markets and the limitations of traditional models in capturing long-term dependencies, this study is particularly timely. It offers a mathematically grounded yet practically motivated approach that integrates memory and uncertainty to reflect the true nature of financial dynamics. The proposed framework can assist economists, policymakers, and financial institutions in developing more resilient strategies and improving predictive accuracy in uncertain economic environments.

2. Preliminaries, Algorithms, and Modeling

Modeling financial systems under uncertainty requires tools capable of capturing both memory-dependent dynamics and stochastic behavior. This section introduces the theoretical foundations and numerical methods employed in this study, focusing on fractional calculus, stochastic noise modeling, and solution algorithms.

2.1. Fractional Derivatives and Memory Effects

Fractional calculus broadens the classical concept of differentiation by allowing the operation to be performed at non-integer (fractional) orders, providing an effective framework for modeling systems exhibiting memory and persistent temporal correlations [5]. Several definitions exist for fractional derivatives; among them, the Caputo formulation is widely preferred in applications due to its compatibility with initial value problems expressed through standard integer-order derivatives. Specifically, the Caputo derivative of a function $f\left(x\right)$ can be formulated as

$$D_c^{\alpha }f\left(x\right)={\displaystyle \frac{1}{\Gamma (n-\alpha )}}{\int }_0^x{\displaystyle \frac{f^{\left(n\right)}\left(t\right)}{{(x-t)}^{\alpha -n+1}}}dt,\mathrm{for}n-1\le \alpha <n,$$

(1)

where $\Gamma (·)$ represents the Gamma function and n is a positive integer ($n\in \mathbb{N}$). This formulation introduces memory into the system, as the rate of change at a given point depends on the function’s history.

This memory effect allows fractional derivatives to model long-term dependencies, which are especially relevant in financial systems where past events influence future outcomes. In this context, fractional-order modeling provides a natural framework to represent the cumulative effects of past decisions, shocks, or trends, as often observed in interest rate dynamics, investment cycles, and asset prices.

2.2. Stochastic Modeling: Gaussian and Fractional Gaussian Noise

To reflect real-world financial uncertainty, stochastic inputs were introduced in the form of Gaussian and fractional Gaussian noise.

Gaussian noise (GN): A classical white noise process $W\left(t\right)$, where increments are normally distributed as

$$W(t+\Delta t)-W\left(t\right)\sim \mathcal{N}(0,{\sigma }^2\Delta t),$$

(2)

was used to represent short-term, uncorrelated fluctuations [7].

Fractional Gaussian noise (fGn): Fractional Gaussian noise (fGn) generalizes classical Gaussian noise (GN) to account for long-range dependence in stochastic processes. It is formally defined as the discrete increment of a fractional Brownian motion $B_H\left(t\right)$:

$$X_H\left(t\right)=B_H(t+1)-B_H\left(t\right),$$

(3)

where the Hurst index $H\in (0,1)$ quantifies the degree of memory in the process. When $H=0.5$, the behavior reduces to standard white noise, while $H>0.5$ indicates positive correlation between increments [12].

The Hurst index H plays a central role in determining the memory characteristics of fGn. Values exceeding 0.5 suggest persistent behavior, where large fluctuations are likely to be followed by similar ones. Conversely, $H<0.5$ reflects anti-persistent dynamics, characterized by a tendency for reversals in the series. These properties make fGn a valuable tool for representing financial time series that exhibit long-term dependencies and volatility clustering.

2.3. Numerical Methods for Stochastic and Fractional Systems

Given the analytical intractability of most fractional and stochastic systems, numerical approximation methods are essential.

Numerical approximation via Euler–Maruyama scheme for SDEs: For systems with standard Gaussian noise, the Euler–Maruyama scheme approximates the solution as

$$x_{n+1}=x_n+hf(x_n,t_n)+\sigma W_n,$$

(4)

where h is the time step and $W_n$ represents Gaussian noise with variance proportional to h [13].

Discrete approximation for fractional stochastic differential equations (FSDEs): For systems driven by fGn, the numerical update must account for both the memory in the dynamics and the correlation in the noise:

$$x_{n+1}=x_n+hf(x_n,t_n)+\sigma X_H\left(n\right),$$

(5)

where $X_H\left(n\right)$ is a sample of fractional Gaussian noise with a specified Hurst exponent H [14]. This formulation allows simulation of systems that exhibit both memory-dependent evolution and persistent stochastic fluctuations.

These mathematical tools and algorithms formed the computational foundation for modeling and simulating both the ordinary and fractional-order financial systems analyzed in this work.

2.4. Modeling

To describe the complex dynamics of financial systems, we considered a nonlinear model that captures interactions among key economic indicators such as interest rate, investment demand, price index, and profit margin. A four-dimensional ordinary differential system was first formulated to represent these dynamics, as presented in the study by Malaikah and Al-Abdali [15]. The system is given by

$$\left\{\begin{array}{cc}x\prime \left(t\right)\hfill & =z+(y-a)x+u,\hfill \\ y\prime \left(t\right)\hfill & =2-by-x^2,\hfill \\ z\prime \left(t\right)\hfill & =xy-x-cz,\hfill \\ u\prime \left(t\right)\hfill & =-dxy-gu,\hfill \end{array}\right.$$

(6)

where $x\left(t\right)$, $y\left(t\right)$, $z\left(t\right)$, and $u\left(t\right)$ represent the interest rate, investment demand, price index, and average profit margin, respectively. The parameters $a,b,c$ are non-negative constants, while $d>0$ and $g>0$ characterize the strength of nonlinear interaction and dissipation.

To enhance the realism of the model and account for the memory effects inherent in economic processes, the integer-order derivatives in system (6) are replaced by Caputo fractional derivatives of order $q\in (0,1]$. This leads to the following fractional-order system:

$$\left\{\begin{array}{cc}{}_0{}^{C}D^{q}x\left(t\right)\hfill & =z+(y-a)x+u,\hfill \\ {}_0{}^{C}D^{q}y\left(t\right)\hfill & =2-by-x^2,\hfill \\ {}_0{}^{C}D^{q}z\left(t\right)\hfill & =xy-x-cz,\hfill \\ {}_0{}^{C}D^{q}u\left(t\right)\hfill & =-dxy-gu,\hfill \end{array}\right.$$

(7)

where the Caputo derivative of order q allows the system to capture long-term dependencies and nonlocal behavior, which are crucial in modeling real financial markets. When $q=1$, the classical system (6) is recovered.

3. Analysis of Noise on Ordinary Financial Systems

Financial systems are influenced by various external factors that introduce noise into their dynamics. This section examines how noise impacts system stability and sensitivity by comparing two scenarios: one without noise and one with noise [1,4].

3.1. Modification of the System

Financial systems frequently experience disruptions arising from factors like market fluctuations and regulatory interventions [2,3]. To account for these effects, bounded random disturbances are introduced into the system, altering its dynamic behavior. Consequently, the perturbed financial model based on Equation (6) is expressed as

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=z+(y-a)x+u+w_x\left(t\right),\hfill \\ \dot{y}\left(t\right)=1-by-x^2+w_y\left(t\right),\hfill \\ \dot{z}\left(t\right)=xy-x-cz+w_z\left(t\right),\hfill \\ \dot{u}\left(t\right)=-dxy-gu+w_u\left(t\right),\hfill \end{array}\right.$$

(8)

where the noise terms $w_x\left(t\right),w_y\left(t\right),w_z\left(t\right),w_u\left(t\right)$ satisfy the following bound:

$$\parallel w_i\left(t\right)\parallel \le {ϵ}_i,{ϵ}_i>0,i\in \{x,y,z,u\}.$$

(9)

This constraint ensures that the uncertainties or external noise in the system remain within a predefined bound, allowing for a more controlled and realistic analysis of system stability.

3.2. Computational Approach and System Parameters

The nonlinear financial system described in (8) was numerically simulated using MATLAB on line [8] to investigate its dynamic behavior under both deterministic and stochastic conditions. The following parameter values were employed in all simulations:

$$a=0.1,b=0.1,c=1.2,d=0.1,g=0.15.$$

These values were selected based on the work of Xia Lu [16], where they were shown to generate complex dynamical behaviors such as chaos and periodicity in a four-dimensional financial system model. The adoption of these parameters provided consistency with the established literature and facilitated a realistic representation of market dynamics under uncertainty.

To analyze the effect of external disturbances, two simulation scenarios were considered:

1. With noise: The system was subjected to bounded external disturbances, where each noise term $w_i\left(t\right)$, for $i\in \{x,y,z,u\}$, satisfied the condition

$$\parallel w_i\left(t\right)\parallel \le {ϵ}_i,\mathrm{with}{ϵ}_i=0.6.$$

2. Without noise: The system was evaluated in a deterministic setting by setting

$${ϵ}_i=0,\forall i\in \{x,y,z,u\}.$$

This comparative framework allowed for a comprehensive assessment of the system’s stability characteristics and its sensitivity to external perturbations, thus offering insights into the robustness of the financial system under various operational conditions.

3.3. Results and Discussion

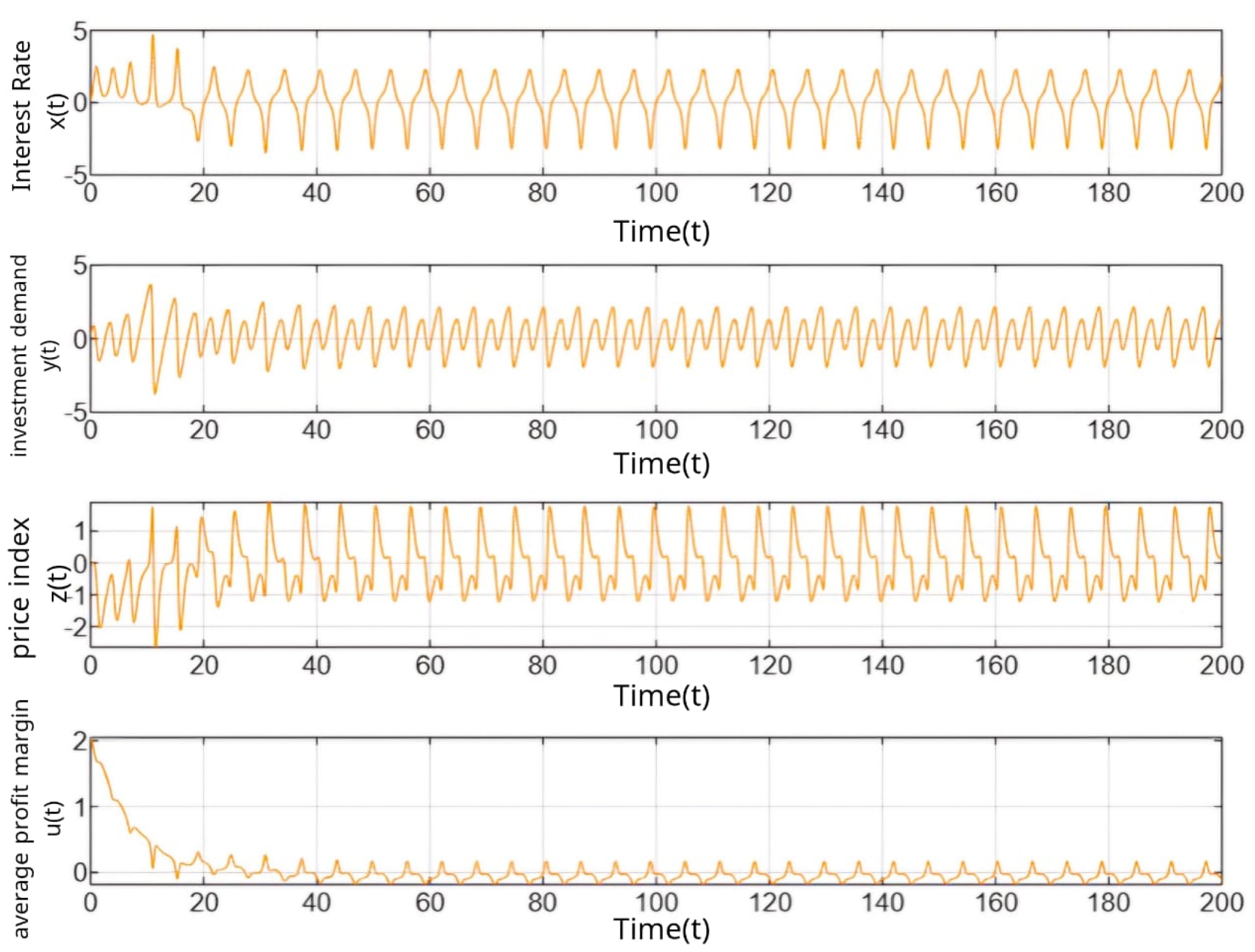
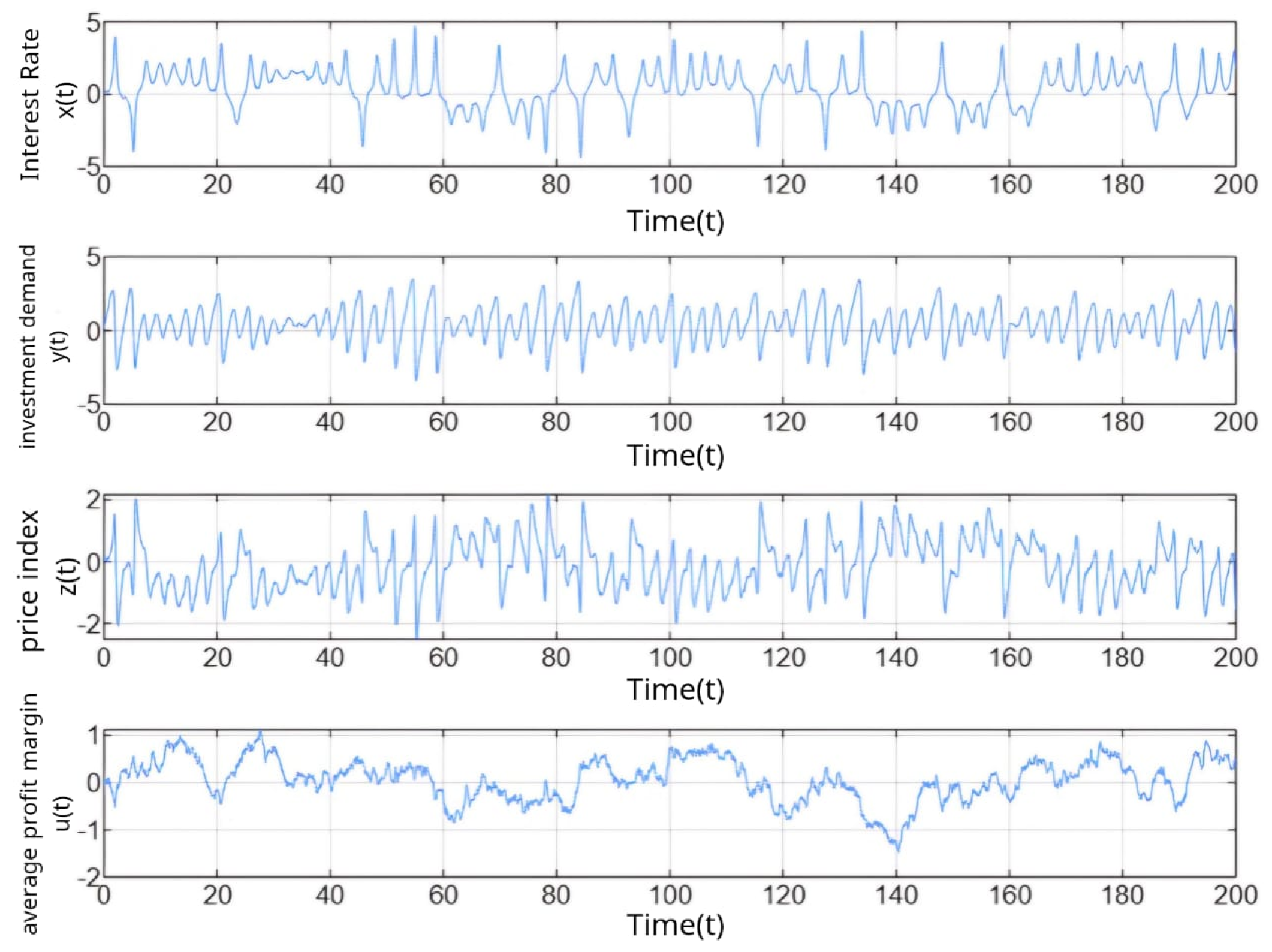
In order to assess how bounded noise influenced the dynamic behavior of the financial model (8), numerical experiments were performed under two conditions: in the presence and absence of noise. Figure 1 and Figure 2 display the trajectories of the system variables $x\left(t\right)$, $y\left(t\right)$, $z\left(t\right)$, and $u\left(t\right)$ across the time span $t\in [0,200]$.

• Without noise: Figure 1 illustrates the deterministic case ($ϵ=0$), where all the variables exhibited smooth, bounded oscillations. The system tended toward a periodic regime, and the control input $u\left(t\right)$ decayed quickly to near zero, indicating stable behavior without external disturbances.
• With noise: Figure 2 depicts the system’s response when subjected to bounded noise ($ϵ=0.6$). The dynamic components $x\left(t\right)$, $y\left(t\right)$, and $z\left(t\right)$ demonstrated sustained oscillations accompanied by irregular variations, highlighting the influence of stochastic disturbances. Although fluctuations were evident, all the states remained confined within finite bounds and $u\left(t\right)$ continued its decaying trend, displaying only minor residual oscillations, which indicates the resilience of the system.

The results show that while the deterministic system converged toward a periodic steady state, the presence of bounded noise introduced irregularities and increased complexity. However, all the state variables remained bounded, confirming the system’s stability under the disturbance constraints (9) and demonstrating its robustness in uncertain financial environments.

3.4. Sensitivity Analysis of System Parameters

To examine the stability of the model under uncertainties in parameter estimation, a sensitivity study was carried out by perturbing the principal parameters $(a,b,c,d,g)$ within a range of $\pm 20\%$ around their baseline values. The objective was to determine the extent to which such deviations influence the system’s dynamic response, particularly focusing on the evolution of $x\left(t\right)$ (representing the interest rate), $y\left(t\right)$ (representing the investment demand), $z\left(t\right)$ (representing the price index), and $u\left(t\right)$ (representing the profit margin).

The results indicate the following:

• The parameter a (saving amount) significantly influenced the initial growth rate of $x\left(t\right)$, with lower values producing faster oscillations.
• The parameter b (cost per investment) directly affected the damping behavior of $y\left(t\right)$, where higher values tended to stabilize the investment component.
• The parameter c (elasticity of demand) modified the decay and volatility patterns in $z\left(t\right)$.
• The parameters d and g governed the evolution of $u\left(t\right)$, where increased values led to more rapid convergence to equilibrium levels.

These observations confirm that while the model was sensitive to certain parameter changes, its overall qualitative behavior—such as boundedness and oscillatory dynamics—remained intact. This suggests that the model is reasonably robust for practical financial simulations.

4. Fractional Systems with Gaussian Noise

Fractional-order systems effectively model memory-dependent processes by incorporating fractional derivatives, offering greater flexibility than integer-order models [5,17]. These systems have been widely used in engineering, physics, and finance to describe real-world phenomena that exhibit long-range dependencies and nonlocal dynamics [6].

4.1. Modification of the System with FGN

To account for stochastic fluctuations, we have introduced FGN into the system (7). The modified equations include a Noise term ${\xi }_H\left(t\right)$ with a Hurst exponent H, representing memory effects [12]. The system is given by

$$\left\{\begin{array}{c}{}_0{}^{C}D^{q}x\left(t\right)=z+(y-a)x+u+{\sigma }_x{\xi }_H\left(t\right),\hfill \\ {}_0{}^{C}D^{q}y\left(t\right)=2-by-x^2+{\sigma }_y{\xi }_H\left(t\right),\hfill \\ {}_0{}^{C}D^{q}z\left(t\right)=xy-x-cz+{\sigma }_z{\xi }_H\left(t\right),\hfill \\ {}_0{}^{C}D^{q}u\left(t\right)=-dxy-gu+{\sigma }_u{\xi }_H\left(t\right),\hfill \end{array}\right.$$

(10)

where ${\sigma }_x,{\sigma }_y,{\sigma }_z,{\sigma }_u$ control the noise intensity for each variable. The inclusion of FGN helps us study how randomness impacts system behavior.

The Hurst exponent H determines the correlation in noise. We set $H=0.7$ to model long-term dependence, which is particularly relevant in financial systems, where market fluctuations exhibit memory effects and long-range correlations [6].

4.2. Computational Approach and System Parameters

To ensure a fair and consistent comparison, the same parameter values employed in the ordinary system were also used in this section.

To analyze the impact of stochastic perturbations, two scenarios were considered:

With noise: The system was subjected to fractional Gaussian noise with the following intensities:

$${\sigma }_x=0.6,{\sigma }_y=0.6,{\sigma }_z=0.6,{\sigma }_u=0.6.$$

Without noise: The system was examined in a purely deterministic setting, where the noise intensities were set to

$${\sigma }_x=0,{\sigma }_y=0,{\sigma }_z=0,{\sigma }_u=0.$$

This configuration enabled a clear comparison between the stochastic and deterministic dynamics, providing insight into how random disturbances impact both the system’s stability and its overall behavior when operating under identical parameter settings.

4.3. Results and Discussion

The system was analyzed under two distinct scenarios to evaluate the influence of fractional Gaussian noise (fGn) on its dynamic behavior.

• Without noise:
  Figure 3 shows the fractional-order system without noise. The dynamic states $x\left(t\right)$, $y\left(t\right)$, and $z\left(t\right)$ exhibited regular, periodic oscillations with mild damping from the memory effect. The variable $u\left(t\right)$ remains bounded with smooth, low-amplitude fluctuations, indicating stable and predictable system behavior.

• With fGn noise:
  Figure 4 illustrates the system under fGn noise ($ϵ=0.6$). The state variables became more irregular and less predictable; $x\left(t\right)$ and $y\left(t\right)$ lost periodicity with noticeable spikes, while $z\left(t\right)$ fluctuated rapidly. The variable $u\left(t\right)$ showed continuous random-like motion, reflecting the system’s response to persistent noise.
  These observations are consistent with findings from [11,18], where systems subjected to long-memory stochastic disturbances exhibited extended deviations and reduced convergence to equilibrium. Our results further demonstrate that the presence of fGn significantly amplifies the effect of noise compared to ordinary Gaussian noise, reinforcing the need for memory-aware models in financial dynamics.

This comparison clearly demonstrates that the inclusion of fGn affects the system’s regularity and stability, leading to increased complexity and reduced predictability. Such analysis is essential for understanding the system’s response to random external influences within a fractional-order framework.

5. Comparison of Results: Ordinary vs. Fractional-Order Financial Systems

This section provides a comparative analysis of the ordinary and fractional-order financial systems under both deterministic and stochastic conditions. The aim is to understand how the introduction of memory via fractional derivatives, along with different noise types, influences system behavior and stability.

Structured Behavior in Fractional Systems:

Fractional-order systems show smoother and more regular responses due to their memory effect. The Caputo derivative allows current states to depend on past values, which helps reduce abrupt changes and noise sensitivity [19,20]. This leads to more stable and structured dynamics compared to ordinary systems, which react only to present inputs.

5.1. Response to Noise: Short-Term vs. Long-Term Effects

Ordinary System:

• Exhibits short-term deviations when exposed to bounded noise.
• Gradually returns to its stable oscillatory regime, indicating fast recovery [21].

Fractional-Order System:

• Experiences more persistent and irregular fluctuations under fGn.
• The memory effect amplifies the influence of noise, leading to long-lasting deviations [19].

5.2. Implications of Derivative Type and Noise Structure

The use of Caputo fractional derivatives introduces nonlocal memory effects [20], making the system more responsive to persistent stochastic inputs. When combined with fGn, this results in complex, less predictable dynamics. In contrast, the ordinary system reacts to noise in a more localized and transient manner.

5.3. Key Findings and Practical Insights

1.

Resilience to Noise:

• The ordinary system shows strong resilience and rapid return to equilibrium, similar to short-term monetary models used in stable economic periods.
• The fractional system is more sensitive and requires longer to stabilize, reflecting real-world phenomena like prolonged volatility after financial crises.

2.

Behavioral Structure:

• The ordinary system maintains a regular oscillatory pattern, aligning with models that assume rapid mean reversion.
• The fractional system exhibits richer but more irregular dynamic structures, capturing market behaviors observed during persistent shocks, such as during the 2008 crisis.

3.

Modeling Real-World Financial Systems:

• Fractional-order models capture long-term dependencies in financial behavior [7], important for modeling delayed effects in markets.
• Ordinary models may suit short-term forecasting where historical influence is limited and immediate policy actions dominate outcomes.

These results show the balance between keeping financial models simple and making them realistic. Ordinary models are easier to handle and more stable, but they might miss the long-lasting effects of major events. In comparison, fractional-order models, by adding memory effects, can better describe the complex behavior of markets during long periods of uncertainty, like global crises or economic downturns caused by pandemics.

6. Financial Interpretation of Results

Understanding the behavior of financial systems under deterministic and stochastic conditions provides valuable insights into market dynamics, resilience, and policymaking. The results obtained from both ordinary and fractional-order models highlight how different structural properties—such as memory effects and noise sensitivity—can influence key economic variables, including interest rates, investment demand, price levels, and profit margins.

6.1. Impact of Noise on Financial Stability

External shocks such as policy shifts, inflationary pressure, or investor sentiment often introduce uncertainty into financial systems [2,3]. In the analyzed models, introducing bounded stochastic noise produced observable fluctuations across all state variables. The ordinary system demonstrated short-term volatility with a tendency to return to baseline behavior, while the fractional-order system exhibited more persistent disturbances—consistent with real-world financial environments where historical dependencies intensify market reactions [22]:

• Interest Rates: Fluctuations in $x\left(t\right)$, representing interest rates, reflect sensitivity to random shocks such as monetary policy changes or inflation. In both models, interest rates remained bounded, but the presence of noise disrupted their regularity—more so in the fractional case.
• Investment Demand: The variable $y\left(t\right)$ showed strong sensitivity to stochastic influence, aligning with theories that link investment activity to investor confidence and perceived risk [23]. This behavior emphasizes the need for responsive fiscal tools to stabilize investment under uncertain conditions [24].

Real-World Contextualization:

These findings are highly relevant in the context of real financial crises. For instance, during the COVID-19 pandemic in 2020 global markets experienced extended volatility and slow recovery periods due to investor uncertainty and delayed policy reactions. The persistent irregular behavior observed in the fractional-order model under fGn mirrors such prolonged disturbances, suggesting that incorporating memory effects provides a more realistic depiction of financial market behavior during turbulent times.

6.2. Profit Margin Volatility and Economic Resilience

The system variable $u\left(t\right)$, representing average profit margins, was particularly impacted by noise. In the absence of disturbances, $u\left(t\right)$ decayed smoothly toward a low equilibrium level, indicating self-regulating profitability. However, under stochastic conditions—especially in the fractional system—$u\left(t\right)$ exhibited sustained irregular behavior, mirroring real-world scenarios of prolonged profit instability during economic turbulence [25]:

• These dynamics correspond to the behavior predicted by models incorporating uncertainty, such as stochastic volatility frameworks [26].
• For firms operating in volatile environments, the results underscore the importance of financial planning, adaptive pricing strategies, and risk management to maintain profitability.

Application to Emerging Markets:

An important area where the fractional-order framework can be effectively applied is the study of cryptocurrency markets. These digital currencies are characterized by extreme volatility, persistent speculative behavior, and pronounced memory effects. The irregular, non-cyclic patterns captured by the fractional model under the influence of fractional Gaussian noise (fGn) closely mirror the real-world dynamics of cryptocurrency prices, positioning the model as a promising tool for deeper exploration in this field.

6.3. Policy Implications and Practical Applications

The outcomes of this research offer valuable insights for financial policy design and regulatory strategies. Given that interest rates and other key economic indicators exhibit different responses to noise under ordinary and fractional-order models, it becomes crucial for central banks to adopt frameworks that incorporate noise sensitivity and memory effects. In particular, fractional models underscore the importance of proactive measures such as adaptable capital buffers and risk management practices that address long-term dependencies [27,28,29].

Modern monetary tools like forward guidance and quantitative easing rely on the idea that markets respond over time, not just instantly. Fractional-order models reflect this behavior by capturing how past conditions shape present outcomes. As such, they can help policymakers better simulate and prepare for delayed reactions in markets, improving long-term planning and financial stability.

7. Challenges and Limitations

This study has several limitations worth noting. The use of Caputo fractional derivatives introduces memory effects that add mathematical complexity and make analytical solutions difficult [5]. Since no closed-form solutions exist, the results depend on numerical methods, which are sensitive to step size, stability, and approximation errors [6]. Simulations are also computationally demanding, especially for long time spans and high-dimensional models [11].

Additionally, the model simplifies many real-world features by excluding behavioral, political, and macroeconomic factors [2]. Another key limitation is the absence of empirical validation using actual market data. While simulations offer useful insights, testing the model on historical events such as the 2008 crisis or the COVID-19 market shock would help assess its practical relevance and forecasting ability.

8. Future Directions

Future studies could improve the model by using more efficient numerical methods and testing other types of noise, such as heavy-tailed or regime-switching disturbances. It would also be valuable to apply the model to real financial data from events like the 2008 crisis or the COVID-19 shock, to evaluate its accuracy in practical settings.

In addition, combining ordinary and fractional models may provide a better balance between short-term dynamics and long-term memory. These steps can enhance the model’s use in forecasting and financial policy.

9. Conclusions

This study analyzed the impact of stochastic noise on ordinary and fractional-order financial systems. Under deterministic conditions, both systems remained stable. However, with noise, the ordinary system showed short-term fluctuations, while the fractional system responded with more persistent and irregular behavior due to its memory effect [5,7].

These results show the benefit of including both noise and memory in financial modeling to better reflect real market dynamics. Future work could focus on adaptive control methods, faster numerical techniques, and testing the model with real financial data to improve its practical use [2,6].