Multifractal Characterization of Pore Structure of Coals Using Gas Adsorption Experiment and Mercury Intrusion Porosimetry (MIP)
Abstract
1. Introduction
2. Materials and Methods
2.1. Sampling
2.2. CO2 Adsorption, N2 Adsorption/Desorption and MIP Measurements
2.3. Multifractal Theory
3. Results
3.1. Coal Characteristics
3.2. Pores Structure Property Identified by CO2 Adsorption
3.3. Pores Structure Property Identified by N2 Adsorption
3.4. Pore Structure Properties Identified by MIP
4. Discussion
4.1. Estimation of Compression Coefficient for Coal Matrix
4.2. Correction of MIP PSDs
4.3. Full-Size Pore Structure Analysis
4.4. Multifractal Features of the Corrected PSDs
4.5. Petrophysical Characteristics and Multifractal Parameters
5. Conclusions
- (1)
- The compressibility of the coal matrix significantly impacts MIP data if pressure exceeds 10 MPa. By incorporating low-temperature nitrogen adsorption data, the MIP pore size distribution in the 6 to 135 nm range can be corrected. After correction, the reduction in mesopore volume ranged from 59.85% to 96.31%, and the reduction in macropore volume ranged from 3.11% to 15.53%, with a substantial decrease in mercury intrusion volume compared to uncorrected volumes. The coal matrix compressibility coefficient ranged between 0.78 10−10~3.56 10−10 m2/N.
- (2)
- The full PSD characterization reveals that in sample L1, pore volume is primarily contributed by macropores, with distributions across both micropore and mesopore ranges. In contrast, in samples M1 and H1, pore volume is mainly distributed within the micropore range, with fewer mesopores and some macropore distribution. Approximately 90% of the total specific surface area of the experimental coal specimens is derived from micropores. In general, the distribution of specific surface area exhibits fluctuations with pore size, reaching its maximum value at 0.6 nm.
- (3)
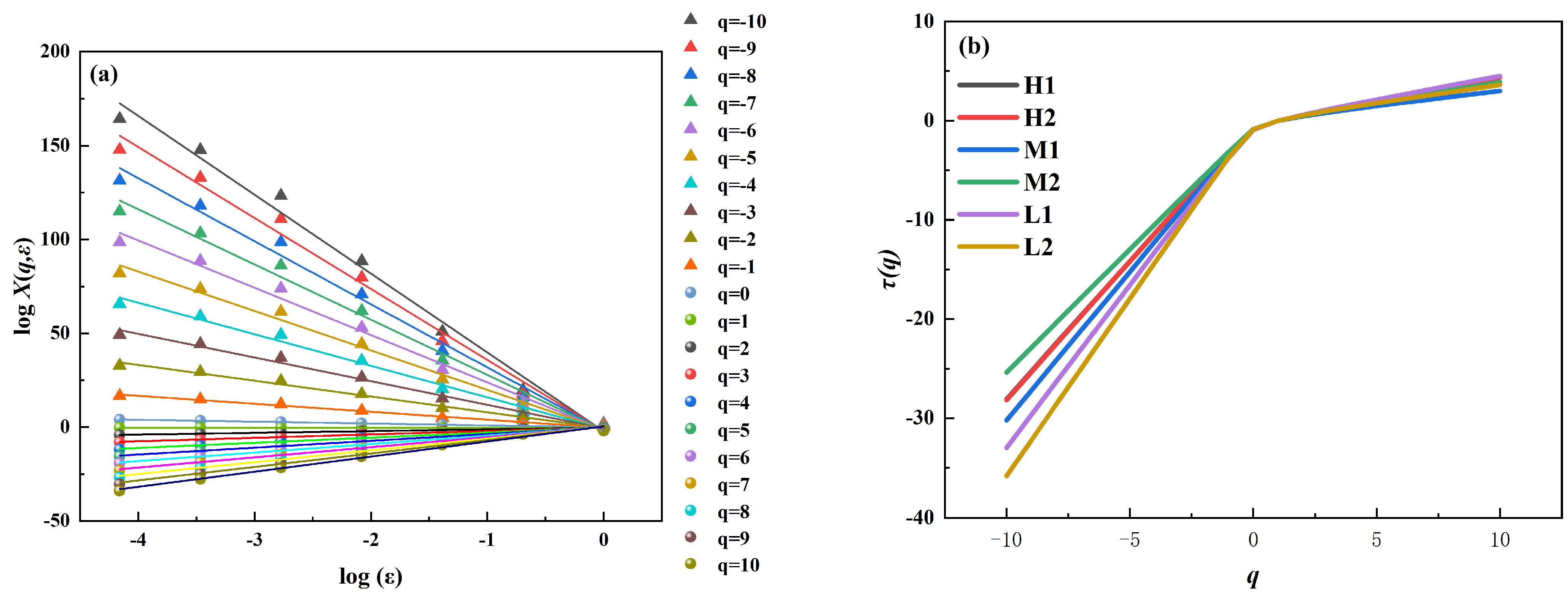
- Multifractal analysis of CO2 data, N2 data, and corrected MIP data indicates that the full pore size distribution exhibits significant multifractal characteristics. The multifractal spectrum exhibits a distinctive convex parabolic form. When q < 0, τ (q) exhibits a noticeable upward trend as q increases, while the growth is more gradual when q > 0. The singularity strength range Δα is between 2.397 and 3.218, and the Hurst index ranges from 0.724 to 0.791.
- (4)
- As the level of coalification rises (i.e., with higher Ro,max values), the multifractal parameters Dmin-D0, D0-Dmax, Δα, and H show a significant negative correlation. Moisture content and volatile matter content are positively correlated with Dmin-D0, Δα, and H, while mineral content has a significant negative correlation with Dmin-D0, Δα, and H. Inertinite content shows a positive correlation with D0-Dmax.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| r | The radius of the pore, nm |
| H | The Hurst index |
| N(ε) | The segmentation of data set |
| ε | The division scale |
| Pi(ε) | The probability density distribution |
| k | The number of boxes |
| i | A positive integer |
| vi(ε) | The cumulative porosity or pore volume of the ith box |
| α | The singularity strength |
| f(α) | The multifractal spectrum or singular spectrum |
| q | The matrix |
| τ(q) | The mass function |
| X(q,ε) | The partition function |
| α | Singularity strength |
| α(q) | Singular strength of the q value |
| Δα | The spectral width |
| αmax | The maximum values of singularity strength |
| αmin | The minimum values of singularity strength |
References
- Moore, T.A. Coalbed methane: A review. Int. J. Coal. Geol. 2012, 101, 36–81. [Google Scholar] [CrossRef]
- Cai, Y.; Liu, D.; Pan, Z.; Yao, Y.; Li, J.; Qiu, Y. Pore structure and its impact on CH4 adsorption capacity and flow capability of bituminous and subbituminous coals from Northeast China. Fuel 2013, 103, 258–268. [Google Scholar] [CrossRef]
- Cai, Y.; Liu, D.; Yao, Y.; Li, J.; Qiu, Y. Geological controls on prediction of coalbed methane of No. 3 coal seam in Southern Qinshui Basin, North China. Int. J. Coal Geol. 2011, 88, 101–112. [Google Scholar] [CrossRef]
- Zheng, S.; Yao, Y.; Liu, D.; Cai, Y.; Liu, Y. Characterizations of full-scale pore size distribution, porosity and permeability of coals: A novel methodology by nuclear magnetic resonance and fractal analysis theory. Int. J. Coal. Geol. 2018, 196, 148–158. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Pajdak, A.; Kudasik, M.; Skoczylas, N.; Wierzbicki, M.; Teixeira Palla Braga, L. Studies on the competitive sorption of CO2 and CH4 on hard coal. Int. J. Greenh. Gas Control 2019, 90, 102789. [Google Scholar] [CrossRef]
- Lu, F.; Liu, C.; Zhang, X.; Jia, B.; Wang, Y.; Liu, S.; Tang, Y.; Liu, J.; Lin, P. Study on full-scale pores characterization and heterogeneity of coal based on low-temperature nitrogen adsorption and low-field nuclear magnetic resonance experiments. Sci. Rep. 2024, 14, 16910. [Google Scholar] [CrossRef]
- Yuan, J.; Chen, J.; Wang, Y.; Xia, J.; Chen, M. Evolution characteristics of pore structure of coal under freeze-thaw cycles combined with scanning electron microscope instrument and nitrogen adsorption experiment. Energy Source Part A 2023, 46, 424–438. [Google Scholar] [CrossRef]
- Chen, L.; Yuan, M.; Li, B.; Zhang, C.; Lv, Q.; Xu, S.; Geng, J. Effect of hydrofluoric acid on Guizhou anthracite structure modification and response to enhanced hydrolysis and permeability of coal. Energy Sources Part A Recovery Util. Environ. Eff. 2024, 46, 5306–5323. [Google Scholar] [CrossRef]
- Liu, P.; Zhao, Y.; Zhao, Z.; Yang, H.; Nie, B.; He, H.; Li, Q.; Bao, G. Image-based quantitative probing of 3D heterogeneous pore structure in CBM reservoir and permeability estimation with pore network modeling. Int. J. Coal Sci. Technol. 2024, 11, 72. [Google Scholar] [CrossRef]
- Jiang, P.; Cheng, Z.; Huang, J.; Li, G. Analysis of pore-fracture structure evolution and permeability in tar-rich coal under high-temperature pyrolysis using μCT technology. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 104. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, S.; Li, Z.; Guo, S.; Wang, R. Application of Multifractal Theory for Determination of Fluid Movability of Coal-Measure Sedimentary Rocks Using Nuclear Magnetic Resonance (NMR). Fractal Fract. 2023, 7, 503. [Google Scholar] [CrossRef]
- Lin, W.; Zhao, X.; Li, M.; Zhuang, Y. Pore Structure Characterization and Fractal Characteristics of Tight Limestone Based on Low-Temperature Nitrogen Adsorption and Nuclear Magnetic Resonance. Fractal Fract. 2024, 8, 371. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, S.; Wu, J.; Li, Z.; Wang, X. Full-Scale Pore Structure Characterization and Its Impact on Methane Adsorption Capacity and Seepage Capability: Differences between Shallow and Deep Coal from the Tiefa Basin in Northeastern China. Fractal Fract. 2024, 8, 48. [Google Scholar] [CrossRef]
- Guo, X.; Yao, Y.; Liu, D. Characteristics of Coal Matrix Compressibility: An Investigation by Mercury Intrusion Porosimetry. Energy Fuels 2014, 28, 3673–3678. [Google Scholar] [CrossRef]
- Cai, Y.; Li, Q.; Liu, D.; Zhou, Y.; Lv, D. Insights into matrix compressibility of coals by mercury intrusion porosimetry and N2 adsorption. Int. J. Coal Geol. 2018, 200, 199–212. [Google Scholar] [CrossRef]
- Krohn, C.E.; Thompson, A.H. Fractal sandstone pores: Automated measurements using scanning-electron-microscope images. Phys. Rev. B 1986, 33, 6366–6374. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Tang, D.; Tang, S.; Huang, W. Fractal characterization of adsorption-pores of coals from North China: An investigation on CH4 adsorption capacity of coals. Int. J. Coal. Geol. 2008, 73, 27–42. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, S.; Xun, X.; Wang, H.; Sun, X.; He, M. Pore Structure and Fractal Characteristics of Coal-Measure Sedimentary Rocks Using Nuclear Magnetic Resonance (NMR) and Mercury Intrusion Porosimetry (MIP). Energies 2023, 16, 3812. [Google Scholar] [CrossRef]
- Peng, R.; Yang, Y.; Ju, Y.; Mao, L.; Yang, Y. Computation of fractal dimension of rock pores based on gray CT images. Chin. Sci. Bull. 2011, 56, 3346–3357. [Google Scholar] [CrossRef]
- Zheng, S.; Sang, S.; Yao, Y.; Liu, D.; Liu, S.; Wang, M.; Feng, G. A multifractal-based method for determination NMR dual T2 cutoffs in coals. J. Pet. Sci. Eng. 2022, 214, 110488. [Google Scholar] [CrossRef]
- Li, W.; Liu, H.; Song, X. Multifractal analysis of Hg pore size distributions of tectonically deformed coals. Int. J. Coal Geol. 2015, 144–145, 138–152. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, X.; Wang, S.; Wang, R.; Wu, J.; Li, Z.; Song, Y. Multifractal characteristics on pore structure of Longmaxi shale using nuclear magnetic resonance (NMR). Geoenergy Sci. Eng. 2024, 241, 213176. [Google Scholar] [CrossRef]
- Zheng, S.; Yao, Y.; Zhang, S.; Liu, Y.; Yang, J. Insights into Multifractal Characterization of Coals by Mercury Intrusion Porosimetry. Energies 2019, 12, 4743. [Google Scholar] [CrossRef]
- GB/T 23561.1-2009; Determination of Coal Rock Physical and Mechanical Properties—Part 1: General Requirements. Standardization Administration of China: Beijing, China, 2009.
- GB/T 6948-2008; Method for Determination of Vitrinite Reflectance of Coal. Standardization Administration of China: Beijing, China, 2008.
- GB/T 212-2008; Proximate Analysis of Coal. Standardization Administration of China: Beijing, China, 2008.
- GB/T 8899-2013; Method for Determination of Maceral Composition and Minerals in Coal. Standardization Administration of China: Beijing, China, 2013.
- GB/T 29172-2012; Method for Determination of Permeability of Coal Reservoir. Standardization Administration of China: Beijing, China, 2012.
- GB/T 21650.3-2011; Evaluation Method of Specific Surface Area and Pore Size Distribution in Low Temperature Physical Adsorption—Part 3: BJH Method for Mesopore Distribution. Standardization Administration of China: Beijing, China, 2011.
- GB/T 29171-2012; Method for Determination of Adsorption Constant of Coal Reservoir. Standardization Administration of China: Beijing, China, 2012.
- Chen, Y.; Qin, Y.; Wei, C.; Huang, L.; Shi, Q.; Wu, C.; Zhang, X. Porosity changes in progressively pulverized anthracite subsamples: Implications for the study of closed pore distribution in coals. Fuel 2018, 225, 612–622. [Google Scholar] [CrossRef]
- Ge, X.; Fan, Y.; Li, J.; Aleem Zahid, M. Pore structure characterization and classification using multifractal theory—An application in Santanghu basin of western China. J. Pet. Sci. Eng. 2015, 127, 297–304. [Google Scholar] [CrossRef]
- Bu, H.; Ju, Y.; Tan, J.; Wang, G.; Li, X. Fractal characteristics of pores in non-marine shales from the Huainan coalfield, eastern China. J. Nat. Gas Sci. Eng. 2015, 24, 166–177. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A Gen. Phys. 1986, 33, 1141–1151. [Google Scholar] [CrossRef]
- Chhabra, A.; Jensen, R.V. Direct determination of the f(alpha) singularity spectrum. Phys. Rev. Lett. 1989, 62, 1327–1330. [Google Scholar] [CrossRef]
- Li, Y.-H.; Lu, G.Q.; Rudolph, V. Compressibility and Fractal Dimension of Fine Coal Particles in Relation to Pore Structure Characterisation Using Mercury Porosimetry. Part. Part. Syst. Charact. 1999, 16, 25–31. [Google Scholar] [CrossRef]
- Debelak, K.; Schrodt, J. Comparison of Pore Structure In Kentucky Coals by Mercury Penetration and Carbon-Dioxide Adsorption. Fuel 1979, 58, 732–736. [Google Scholar] [CrossRef]
- Xu, L.; Liu, C.; Xian, X.; Zhang, D. Compressibility of coal matter and coal pore. Colloids Surf. A-Physicochem. Eng. Asp. 1999, 157, 219–222. [Google Scholar] [CrossRef]
- Caniego, F.; Martín, M.; San José, F. Singularity features of pore-size soil distribution:: Singularity strength analysis and entropy spectrum. Fractals 2001, 9, 305–316. [Google Scholar] [CrossRef]
- Wang, D.; Hu, H.; Wang, T.; Tang, T.; Li, W.; Zhu, G.; Chen, X. Difference between of coal and shale pore structural characters based on gas adsorption experiment and multifractal analysis. Fuel 2024, 371, 132044. [Google Scholar] [CrossRef]
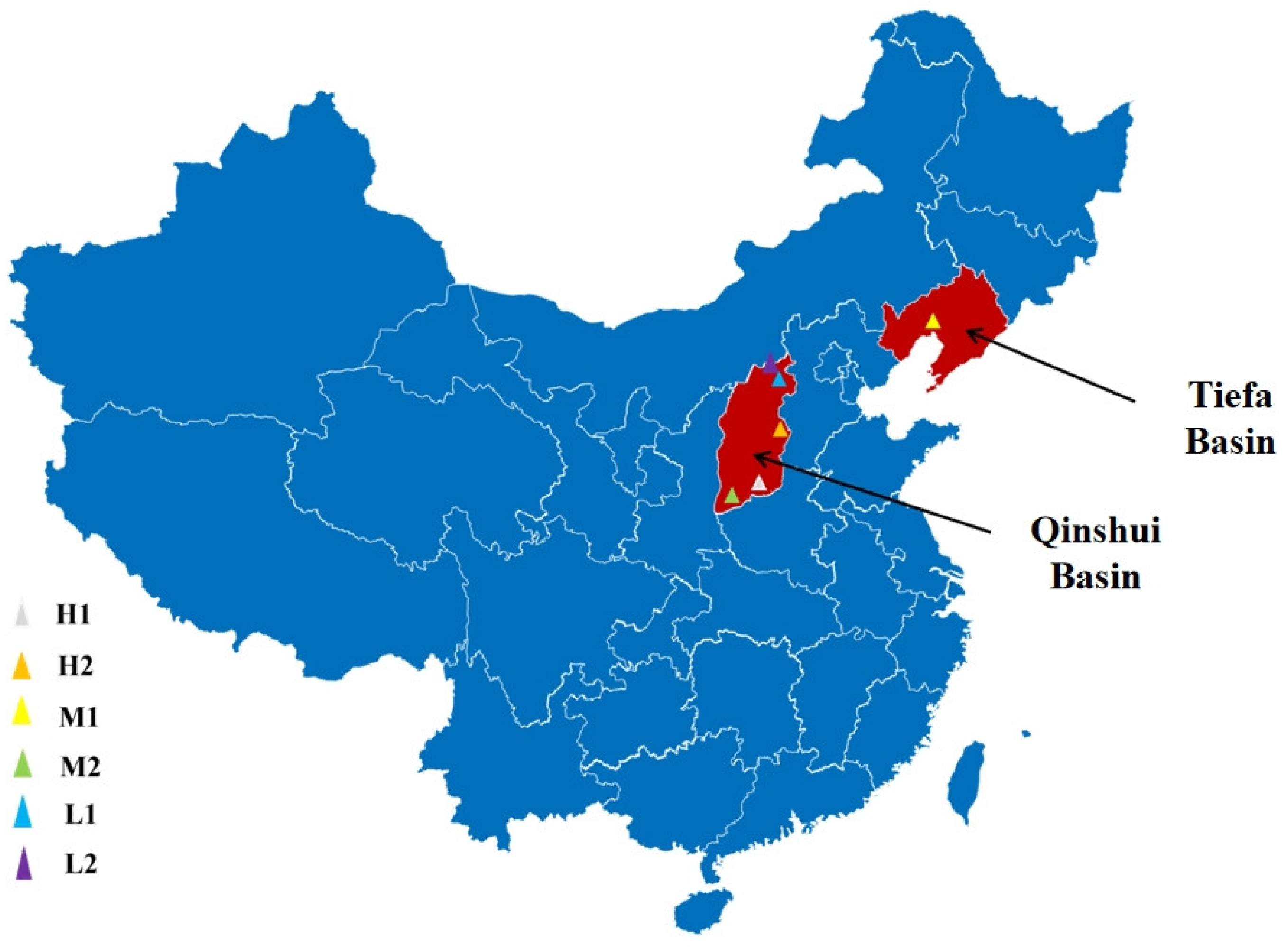

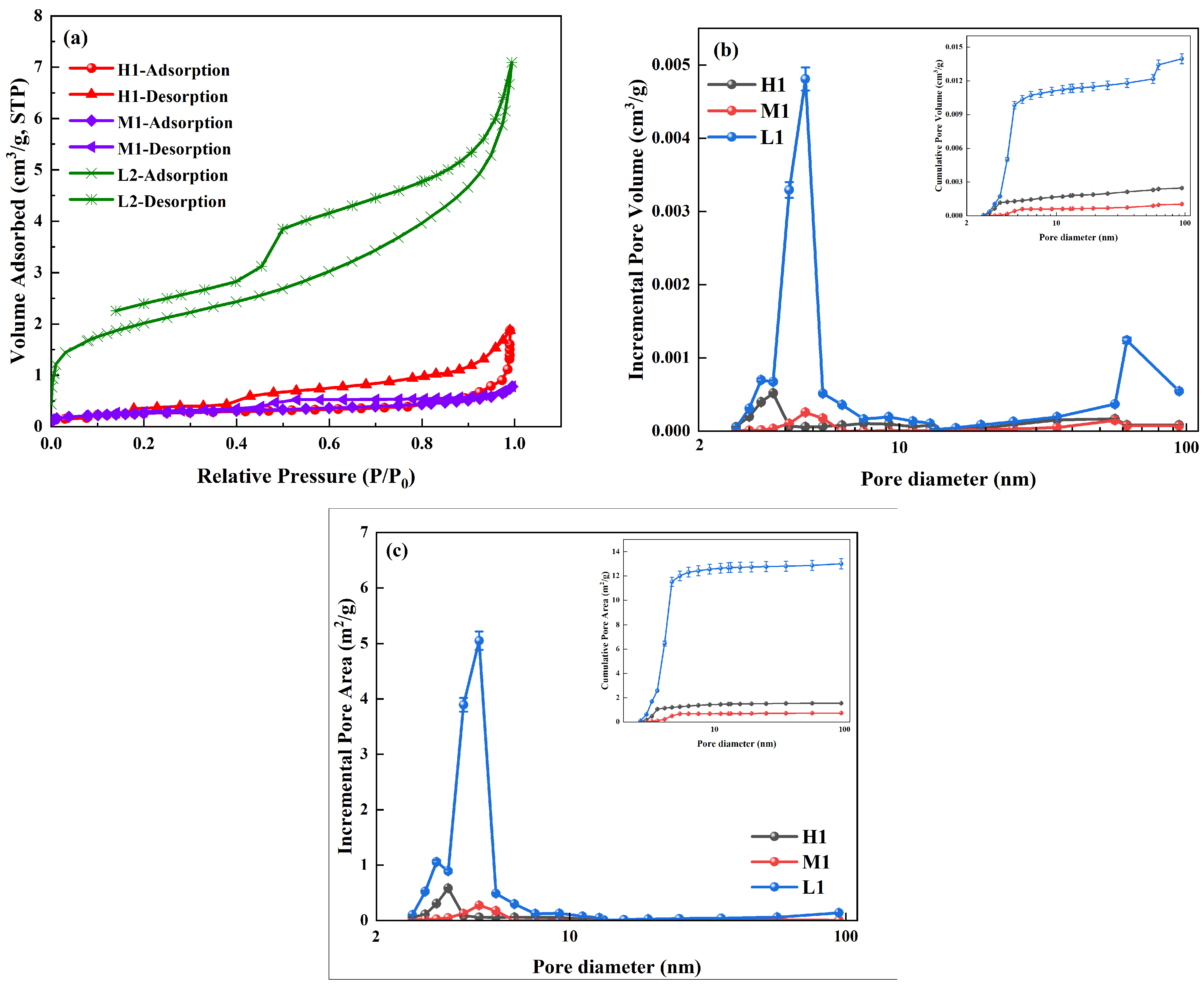


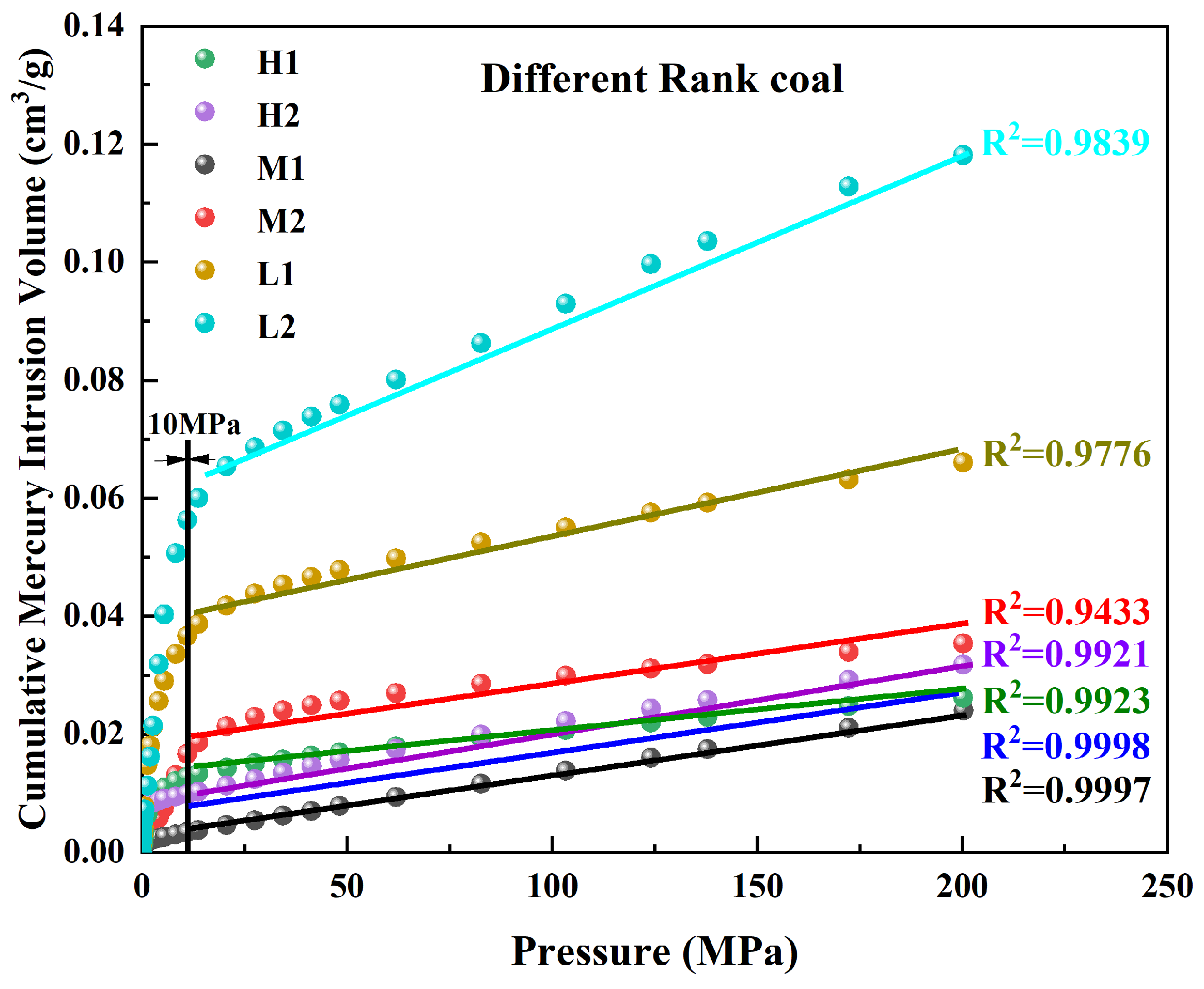
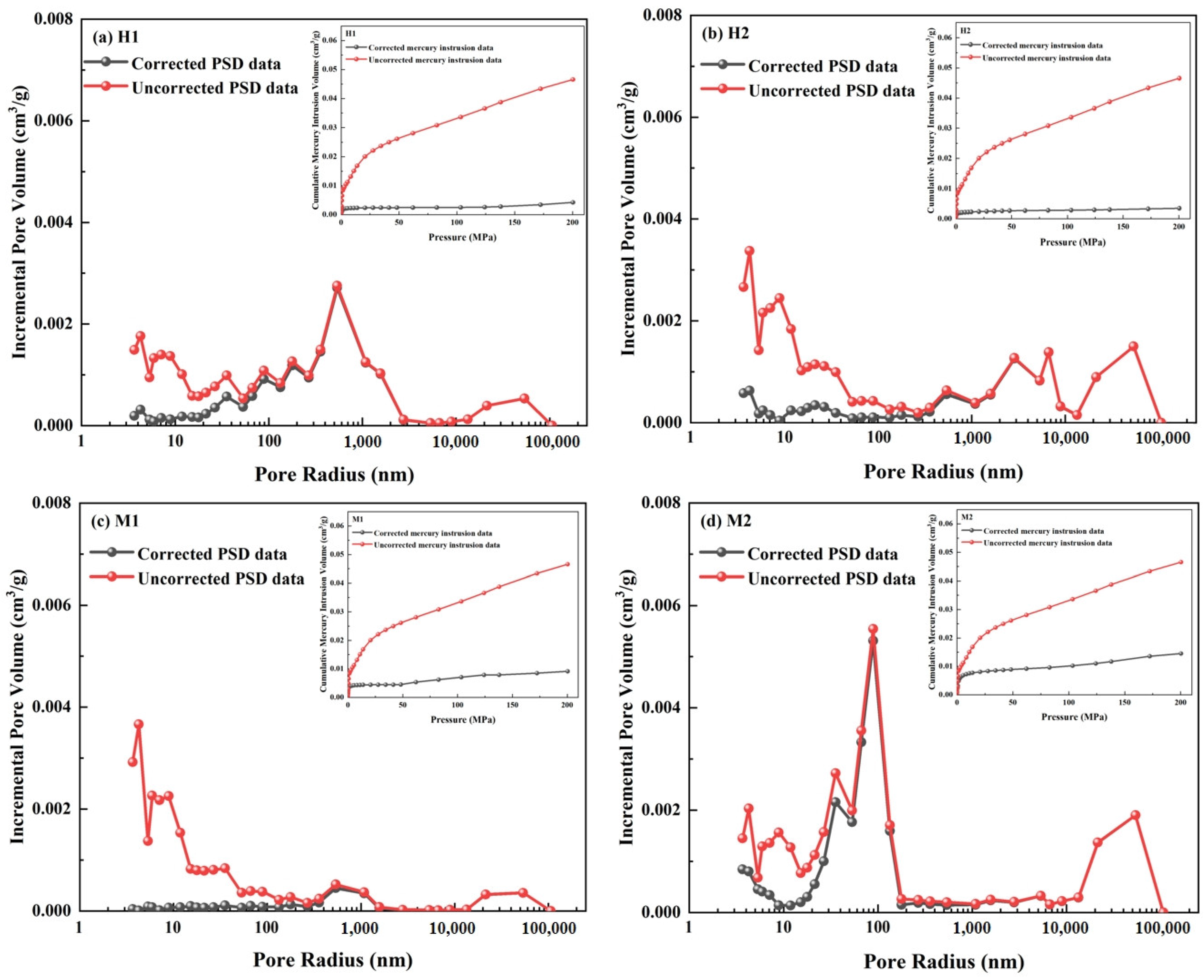




| No. | Ro, Max (%) | Porosity φ (%) | Permeability K (mD) | Proximate Analysis (%) | Coal Composition (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mad | Aad | VMad | FCad | Vitrinite/ Huminite | Inertinite | Exinite | Mineral | ||||
| H1 | 3.28 | 8.68 | 0.76 | 1.94 | 5.56 | 5.41 | 87.09 | 81.2 | 12.3 | 2.2 | 2.6 |
| H2 | 2.40 | 5.89 | 0.93 | 1.87 | 17.70 | 9.43 | 71.00 | 40.3 | 50.6 | 2.8 | 4 |
| M1 | 1.96 | 2.55 | 2.57 | 0.89 | 17.39 | 15.88 | 65.84 | 51.6 | 40.2 | 3.6 | 2.7 |
| M2 | 1.90 | 1.58 | 1.26 | 0.80 | 13.17 | 17.18 | 68.85 | 39.4 | 47.5 | 6.7 | 3.6 |
| L1 | 0.63 | 21.74 | 4.61 | 4.24 | 19.25 | 36.22 | 40.29 | 47.4 | 45.8 | 2.3 | 2.4 |
| L2 | 0.51 | 25.95 | 3.57 | 3.50 | 3.44 | 31.83 | 61.23 | 44.7 | 48.2 | 1.8 | 2.1 |
| Sample No. | MIP | LTNA | Mesopore Volume (cm3/g) | Macropore Volume (cm3/g) | ||||
|---|---|---|---|---|---|---|---|---|
| (m2/N) | Before Correction | After Correction | Before Correction | After Correction | Before Correction | After Correction | ||
| H1 | 11.67 10−5 | 1.56 10−10 | 0.112 10−3 | 0.099 10−3 | 0.0215 | 0.0016 | 0.0103 | 0.0087 |
| H2 | 6.93 10−5 | 0.78 10−10 | 2.518 10−3 | 1.702 10−3 | 0.0129 | 0.0021 | 0.0133 | 0.0125 |
| M1 | 8.84 10−5 | 1.19 10−10 | 0.976 10−3 | 0.298 10−3 | 0.0163 | 0.0006 | 0.0085 | 0.0073 |
| M2 | 8.63 10−5 | 1.31 10−10 | 0.872 10−3 | 0.749 10−3 | 0.0167 | 0.0044 | 0.0186 | 0.0175 |
| L1 | 31.53 10−5 | 3.56 10−10 | 14.349 10−3 | 2.675 10−3 | 0.0581 | 0.0065 | 0.0600 | 0.0559 |
| L2 | 14.38 10−5 | 2.11 10−10 | 8.826 10−3 | 2.794 10−3 | 0.0274 | 0.0110 | 0.0386 | 0.0374 |
| Sample No. | Vtotal/ (cm3·g−1) | V1 (cm3·g−1) | V2 (cm3·g−1) | V3 (cm3·g−1) | Stotal/ (m2·g−1) | S1 (m2·g−1) | S2 (m2·g−1) | S3 (m2·g−1) |
|---|---|---|---|---|---|---|---|---|
| H1 | 0.0626 | 0.0518 | 0.0022 | 0.0086 | 161.67 | 160.09 | 1.54 | 0.04 |
| H2 | 0.0397 | 0.0248 | 0.0028 | 0.0121 | 83.09 | 81.55 | 1.43 | 0.10 |
| M1 | 0.0261 | 0.0178 | 0.0010 | 0.0073 | 57.95 | 57.17 | 0.74 | 0.04 |
| M2 | 0.0231 | 0.0157 | 0.0023 | 0.0051 | 51.56 | 51.12 | 0.17 | 0.27 |
| L1 | 0.0959 | 0.0278 | 0.0138 | 0.0543 | 107.20 | 92.60 | 13.86 | 0.73 |
| L2 | 0.0635 | 0.0194 | 0.0077 | 0.0364 | 71.60 | 65.54 | 5.69 | 0.37 |
| Sample No. | Dmax | Dmin | D0 | D1 | D2 | Dmin-D0 | D0-Dmax | Δα | H |
|---|---|---|---|---|---|---|---|---|---|
| H1 | 0.483 | 2.553 | 0.857 | 0.695 | 0.533 | 1.696 | 0.374 | 2.397 | 0.767 |
| H2 | 0.483 | 2.562 | 0.882 | 0.712 | 0.541 | 1.680 | 0.399 | 2.342 | 0.770 |
| M1 | 0.333 | 2.748 | 0.848 | 0.648 | 0.448 | 1.900 | 0.515 | 2.705 | 0.724 |
| M2 | 0.432 | 2.309 | 0.866 | 0.685 | 0.505 | 1.444 | 0.433 | 2.082 | 0.752 |
| L1 | 0.499 | 2.998 | 0.948 | 0.765 | 0.583 | 2.051 | 0.449 | 2.824 | 0.791 |
| L2 | 0.401 | 3.257 | 0.887 | 0.708 | 0.568 | 2.370 | 0.486 | 3.218 | 0.784 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Chen, F.; Yue, S.; Hu, J.; Ding, H.; Lu, A. Multifractal Characterization of Pore Structure of Coals Using Gas Adsorption Experiment and Mercury Intrusion Porosimetry (MIP). Fractal Fract. 2025, 9, 183. https://doi.org/10.3390/fractalfract9030183
Wang S, Chen F, Yue S, Hu J, Ding H, Lu A. Multifractal Characterization of Pore Structure of Coals Using Gas Adsorption Experiment and Mercury Intrusion Porosimetry (MIP). Fractal and Fractional. 2025; 9(3):183. https://doi.org/10.3390/fractalfract9030183
Chicago/Turabian StyleWang, Shuaidong, Fengyin Chen, Shenghui Yue, Jing Hu, Hongrui Ding, and Anhuai Lu. 2025. "Multifractal Characterization of Pore Structure of Coals Using Gas Adsorption Experiment and Mercury Intrusion Porosimetry (MIP)" Fractal and Fractional 9, no. 3: 183. https://doi.org/10.3390/fractalfract9030183
APA StyleWang, S., Chen, F., Yue, S., Hu, J., Ding, H., & Lu, A. (2025). Multifractal Characterization of Pore Structure of Coals Using Gas Adsorption Experiment and Mercury Intrusion Porosimetry (MIP). Fractal and Fractional, 9(3), 183. https://doi.org/10.3390/fractalfract9030183





