Abstract
This study explores the motivational factors behind alcohol consumption and its societal impacts. It identifies key reasons for drinking, such as improving sociability, boosting confidence, coping with challenges, participating in rituals, and seeking detoxification. The study highlights the substantial societal harm caused by the use of alcohol and drugs, with a particular emphasis on the increase in sexual violence, both within and outside families, as a result of impaired behavior. In this work, we present a newly developed mathematical model within the Caputo fractional framework, designed to reflect the lifestyle and behaviors of individuals in the alcohol model. We analyze the existence and uniqueness of solutions using the Lipschitz growth condition and fixed point theory. In addition, we explore equilibrium points, compute basic reproduction numbers, and explore the Hyers–Ulam stability of the alcohol model. Finally, we develop a numerical scheme for computational analysis of the proposed fractional model.
Keywords:
alcohol; Caputo fractional derivative; existence; uniqueness; Hyers–Ulam stability; epidemic; numerical methods MSC:
28A80; 34A08; 92C45; 34K20; 65L07
1. Introduction
In recent years, numerous challenges in the natural sciences, engineering, economics, and medicine have prompted the exploration of mathematical models that incorporate rates of change. These models are essential for analyzing problems where the behavior of a solution evolves over time [1,2]. Ordinary differential equations serve as a fundamental framework for such models, as they describe systems involving derivatives, applicable to functions where the concept of differentiation is well-defined. Differential equations are commonly used to represent dynamic systems, including physical processes like particle motion, chemical reactions, elastic vibrations, fluid dynamics, electromagnetic oscillations, and even financial phenomena. The study of these models constitutes a vital area of applied mathematics, often referred to as mathematical modeling [3,4,5]. This field highlights the power of mathematics in collecting, interpreting, and generalizing scientific data to understand and predict complex systems.
Alcohol consumption is a widespread behavior in many societies and often leads to addiction for a significant portion of the population. Alcohol addiction has been extensively studied due to its profound physical and psychological impacts. However, traditional models primarily focus on the mechanisms of addiction and strategies to control alcohol consumption, frequently overlooking the depressive tendencies that often accompany addiction. Depression, often co-occurring with addiction, intensifies its adverse effects on individuals’ well-being and further complicates treatment approaches. Understanding the relationship between alcohol addiction and depression is essential for developing comprehensive models that can inform more effective intervention strategies. This study seeks to address this gap by incorporating the effects of depression into models of alcohol addiction, offering a more realistic representation of the challenges faced by individuals dealing with both conditions. Alcohol abuse is on the rise, posing a growing threat to global communities. Among younger generations, the misuse of alcohol is escalating rapidly, often driven by the pursuit of fun and enjoyment. Over recent decades, the consequences of alcohol addiction have extended beyond financial costs, disrupting marriages, family life, and social structures. Alcohol addiction negatively impacts neighborhoods, schools, workplaces, healthcare systems, and society at large. It is a significant risk factor for numerous chronic illnesses and disorders, including certain types of cancer, psychiatric conditions, cardiovascular diseases, and digestive disorders. It also increases the likelihood of diabetes, stroke, and heart disease. In the past two decades, researchers have made considerable efforts to identify the factors contributing to the spread of these harmful effects within society.
Fractional-order mathematical models play a crucial role in representing the dynamic behavior of real-world problems and offer numerous advantages. Compared to conventional integer-order models, fractional-order models are more accurate and reliable as they incorporate hereditary and memory effects along with other properties. Fractional calculus, a generalization of traditional calculus, has been extensively studied over the past two decades. Its primary advantage lies in its ability to account for historical effects through memory, enhancing the analysis and study of real-world phenomena. Fractional calculus has been widely applied in various fields of engineering and science [6,7,8]. It extends the concept of differentiation and integration to fractional orders, enabling more flexible and precise modeling. For example, Zitane [9] proposed an innovative extension involving non-local and non-singular kernels in fractional calculus, introducing fractional operators where the order depends on variables such as time, space, or other factors. Applications of fractional-order models in real-world scenarios are diverse. Jan et al. [10] investigated plant infections and developed preventive strategies for the spread of the yellow virus in red chilli plants. Boulaaras et al. [11] analyzed the dynamics of typhoid fever infections, incorporating the effects of vaccination and carriers. Similarly, Bahi et al. [12] studied the transmission dynamics of sexually transmitted human papillomavirus (HPV) to provide insights for public health interventions. These studies highlight the versatility and effectiveness of fractional calculus in addressing complex problems across various disciplines.
In recent years, fractional analysis has revolutionized problem-solving with mathematical models, offering highly efficient methods that have revitalized mathematics and applied sciences. Fractional analysis provides greater effectiveness than classical techniques, particularly in addressing processes or problems that traditional methods struggle to describe adequately. Developing novel derivative and integral operators has significantly advanced this field, making it a focal point of intensive research [13]. With its wide range of applications, fractional calculus is rapidly gaining popularity and has become the subject of numerous research initiatives. This area has drawn the attention of mathematicians across various disciplines [14]. Previously, analytical and numerical methods were employed to solve problems within the Caputo fractional differential framework. Additionally, researchers have explored the use of fractional derivatives in control systems [15,16,17]. Recent advancements in fractional calculus have opened new avenues for capturing intricate dynamics in various fields. These include economic and environmental mathematical models [18], brain tumour modeling [19], and the transmission dynamics of Lassa fever [20]. Furthermore, researchers have investigated numerical solutions [21] and approximation methods [22] using fractional derivatives, highlighting the versatility and growing impact of this mathematical tool.
The Caputo fractional derivative is a widely used operator in fractional calculus, a branch of mathematical analysis that extends the concept of differentiation to non-integer orders. Unlike classical derivatives, which measure instantaneous rates of change, fractional derivatives incorporate memory effects, making them suitable for modeling complex systems with hereditary properties. The Caputo derivative is defined in terms of an integral operator and a traditional derivative, ensuring compatibility with initial conditions expressed in terms of integer-order derivatives [23,24].
The primary objective of functional equation theory is to establish stability. This field has gained significant attention due to its wide range of applications in both pure and applied mathematics. The foundational problems in this area were introduced by D. H. Hyers and S. M. Ulam in 1940 and later independently revisited by Th. M. Rassias in 1978. Subsequently, researchers identified similar types of stability issues in f-quadratic and f-Cauchy equations [25,26]. The stability problem of the linear functional equation with a scalar coefficient function can be traced back to Ulam [27]. Our study is driven by the motivation to explore Hyers–Ulam stability in mathematical analysis. This research provides a foundation for further investigations into solutions of the contractive functional equation. It is particularly significant as it establishes a connection between the solutions of functional equations and contractive difference equations. Moreover, our work contributes to constructing and analyzing the stability of differential equations associated with contractive functional difference equations, building on our notable success in solving the contractive difference equation.
This paper aims to utilize the Caputo fractional derivative to solve a novel alcohol addiction model and examine its existence, uniqueness, and various Hyers–Ulam stabilities of solutions. A key advantage of the proposed model is its ability to capture a broader range of families with depressive tendencies and addictions. This allows researchers to gain deeper insights into the underlying physical dynamics of the system and make more accurate predictions about its behavior. The study focuses on exploring the impact of alcohol addiction on individuals’ mental health, emphasizing its potential to cause depression at any stage of life. The novelty of this research lies in its detailed analysis of how alcohol addiction can lead to depression through various social and psychological factors. These include social comparison, increased feelings of loneliness, harassment, negative feedback from others, decreased motivation, elevated stress levels, reduced real-life social interactions, and relationship issues. By incorporating these factors into a fractional mathematical model, the study offers a comprehensive understanding of the interplay between alcohol addiction and depression. This relationship is visually represented in Figure 1, which depicts the alcohol model diagram. The proposed mathematical model for alcohol addiction is based on the following hypotheses:
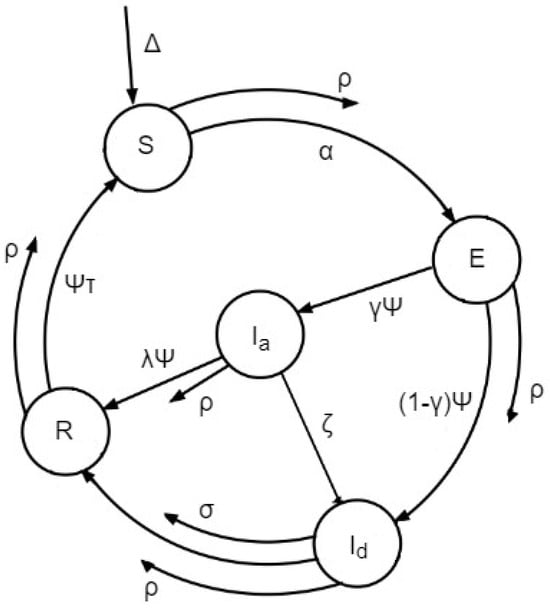
Figure 1.
Schematic diagram of alcohol model.
- The alcohol addiction model is studied within a closed environment.
- Economic status and gender do not influence the risk of alcohol addiction.
- All participants interact with each other uniformly and to the same degree.
- The alcohol consumption of addicted individuals can influence those who are not yet addicted.
- Alcohol use plays a significant role in the spread of depression among addicted individuals, with personal differences either mitigating or intensifying this effect.
To the best of our knowledge, there is a gap in research investigating the Hyers–Ulam stability analysis of the alcohol model with fractional derivative operators. This lack of research highlights the need for more study. To address this gap, this study employs the fractional derivative in the Caputo sense to investigate the Hyers–Ulam stability analysis of the alcohol model with fractional derivative operators. This paper aims to address the gap in research based on the aforementioned facts and motivation. The primary contributions of this work are summarized below:
- Insufficient research has focused on the analysis of the Hyers–Ulam stability, which leads to a gap in the existing literature. Our primary objective is to examine the Hyers–Ulam stability of a fractional-order alcohol model.
- The methodology employs a fixed point approach to examine the existence and uniqueness solution, as well as investigate the Hyers–Ulam stability and highlight other interesting findings related to the stability of this system, which have not been previously explored in this context.
- In addition, this approach simplifies the calculation of approximate solutions for the given problem, enabling us to test and examine the theoretical results using real-world scenarios.
Our contributions seek to address this research gap and bring new perspectives to the field of fractional derivatives. We provide valuable theoretical and numerical results for studying fractional-order differential equations using Caputo sense.
The structure of this paper is organized as follows: Section 2 introduces the mathematical framework of the proposed model. Section 3 presents key definitions, associated concepts, and an overview of a basic computational approach. Section 4 identifies the equilibrium points of the model. Section 5 focuses on finding a unique solution involving the Caputo fractional derivative, while Section 6 demonstrates the Hyers–Ulam stability of the model. Section 7 involves numerical simulations are carried out to illustrate the effect of key parameters on the dynamics of the system using the Adams–Bashforth method. Finally, Section 8 provides a brief conclusion.
2. Model Description for the Alcohol Model
This model categorizes the population into five compartments: Susceptible individuals (S) are those who do not currently consume alcohol but are at risk of starting. Exposed individuals (E) are occasional alcohol users who are at risk of developing an addiction. Addictive individuals () are frequent alcohol users who are currently suffering from addiction. Depressed individuals () are individuals experiencing depression as a result of alcohol consumption. Recovered individuals (R) are those who have completed treatment and recovered from addiction. The total number of individuals (population), denoted by , is given as
Susceptible individuals are recruited into the population at a rate of . Peer pressure from addicted individuals influences these susceptible individuals to use alcohol at a contact rate of , with a possible transmission rate of , leading them to join the exposed class. The exposed population, affected by alcohol use, transitions to the addicted class at a rate of , while the remainder recovers through treatment at a rate of . Addicted individuals become depressed at a rate of , and those who leave treatment or require a second dose also become depressed at a rate of . Depressed individuals either transition to the recovered class through education and/or treatment at a rate of or succumb to depression at a rate of . The probability of achieving recovery through treatment is , and the overall population average death rate is .
Next, we present a novel approach to the proposed model in fractional form (1) given as
along with the initial condition, and .
3. Preliminaries
Here, we review some fundamental concepts of projection techniques that are critical to the depth of this study.
Definition 1
([28]). The Caputo time-fractional derivative of order for a function is defined as
Definition 2.
From the above function, as discussed, the integral fractional operator in the Caputo fractional operator is displayed as
Lemma 1
([29]). Consider , then the solution of fractional differential equation
such that
Here , .
4. Equilibrium Points of Alcohol Model
This section aims to determine the equilibrium points of the alcohol model.
Solving the above set of model (1) yields two equilibrium points in the feasible region. Note that we have
It is seen in the alcohol model that when , there is no infection with the specified values
The reproduction number represents the expected number of secondary infections produced by a single infected individual during their infectious period. If , the infection will not cause an epidemic within the population. Conversely, if , the infection will persist and potentially spread throughout the population. The reproduction number , provides a crucial measure for controlling the spread of the infection.
which implies that
which, with the help of the Jacobi matrices of F and V for the alcohol model, can be rewritten as
Now the matrix is given by,
Therefore, is determined by selecting the dominant eigenvalue from the matrix .
- Here, .
5. Existence and Uniqueness Results
This section aims to discuss the existence and uniqueness of solutions for the alcohol model using a fixed point method.
Suppose that we have a Banach space in which the norm is defined as,
where
If we employ the last relation, then we can write Equation (4) by using (2)
Thanks to Lemma 1 and the solution of Equation (5), this can be expressed in the following form
We now provide some interesting facts for existence: we shall assume that and are true
- (A1) For the constants , such that
- (A2) For the constants £, with then,
The observability of the operator as
Theorem 1.
If the inequalities and hold true, then the system given in has at least one solution.
Proof.
System provides at least one fixed point in the solution representation of the system. The projected problem outcome applies Kransoselki’s fixed point theorem. We split the proof into the following steps:
- Step 1: In this step, we shall prove that the state variables can be displayed in terms of the continuity of the operator T as follows: Suppose that , for , .As a result, the continuity ∇, with the , consequently T is continuous.
- Step 2: In this step, we verify that this requirement for T is bounded. Assume that , the operator T, which satisfies the growth conditions as follows:We characterize to be a bounded subset of B and there exist we have . With the help of the growth condition, it follows that , in the same manner, such thatSo, we reach this goal as is bounded.
- Step 3: In addition, we prove that the continuity of T is continuous. For this purpose, let , such that , we have
- Step 4: Suppose that and , such that
Finally, E is bounded. Therefore, the consider operator is relatively compact, so it is completely continuous. Based on the results obtained, we can infer that the operator T possesses a unique fixed point. □
6. Stability for Solution
Here, we discuss the stability criterion for solutions of the alcohol model . In the following theorem, we prove the Hyers–Ulam stability, which obviously also improves the result of Hyers–Ulam–Rassias stability using the fractional derivative method.
Definition 3.
([30]). Suppose that and assume that Y be any solution of the inequality given by
The solution of the Equation is Hyers–Ulam stable, if there exists a solution for the Equation with the constant and satisfying
will also be generalized Hyers–Ulam stable, if for the function with , such that
Remark 1.
Notice that is termed as solution Equation , if , we have
- 1.
- .
- 2.
- = .
Lemma 2.
Suppose that be a solution of the equation
Then the above relation will be satisfied.
Theorem 2.
The solution of Equation is Hyers–Ulam stable and consequently generalized Hyers–Ulam stable with Lemma 2 if the condition holds .
Proof.
Assume that Y and are a unique solution of Equation , then taking
Then the fractional model is said to be Hyers–Ulam stable. □
Definition 4.
Assume that and let Y be any solution of the inequality given by function
The solution of the Equation is Hyers–Ulam–Rassias stable, if there exists a solution with the constant and satisfy
Remark 2.
If will satisfy Equation , if , we have
- 1.
- .
- 2.
- = .
Lemma 3.
Suppose that be a solution, so we can write it as follows
Then the above expression, as follows Equation yields that
Theorem 3.
The solution of (5) is Hyers–Ulam–Rassias stable and consequently generalized Hyers–Ulam–Rassias stable if the condition holds with the Lemma.
Proof.
Assume that Y and be a unique solution of , then taking
Then the fractional model is said to be the Hyers–Ulam–Rassias stable. □
7. Numerical Scheme
According to model , the numerical scheme of the adopted fractional model using the Adams–Bashforth method demonstrates the technique. We assess the precision of this approach based on the exact results. In this section, we utilize graphs created through numerical simulation. We employed a fractional differential equation nonlinear system to mathematically analyze the alcohol model. Compared to ordinary derivatives, we discover a greater degree of flexibility in the fractional alcohol model. Through numerical simulation, we were able to obtain the compression for various values of n.
Furthermore, it is presumed that the Volterra integral of the above Equation is displayed as
Again integrating the above equation, we gain as
Observe that . By making use of the above scheme for the suggested novel model, we obtain the following solution
Results and Discussion
Using MATLAB 2021a for graphical representation, we simulate the numerical schemes using Equation . Using the initial data and with the parameters given in Table 1, we provide this summary of the findings of a numerical simulation of addiction dynamics. The simulation results indicate that, at the peak of addiction, the proportions of exposed and addicted individuals stabilize at 0.06 and 0.10, respectively. The rapid increase in addiction levels initially causes a rise in the number of depressed individuals, which eventually stabilizes at 0.10. Meanwhile, the percentage of recovered individuals fluctuates over time as the number of exposed, addicted, and depressed individuals decreases. It finally settles at 0.2, with changes in the parameter , as shown in Figure 2.

Table 1.
Parameters.
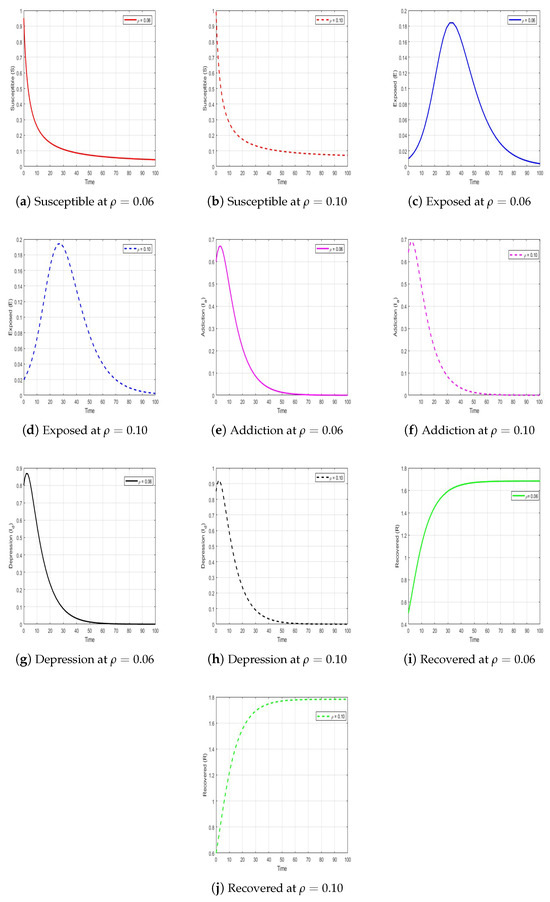
Figure 2.
Dynamical behavior of variables over time with respect to , and R in the context of addiction and depression, considering the variation of the input parameter and .
8. Conclusions
In this study, we used the Caputo fractional derivative to establish a connection between alcohol consumption and the impacts of alcohol addiction. This relationship was formulated as a Caputo fractional differential equation. To validate the authenticity of the proposed model, we verified the existence and uniqueness of the solution. Our analysis reveals that, under specific conditions, the model solution exists and is unique.
The alcohol-free equilibrium point highlights the importance of considering the population’s interplay with addiction and sadness to achieve a more realistic representation. Remarkably, the data generated by our model align closely with the actual observations, reinforcing the reliability of our projections. The inclusion of fractional derivatives has expanded the scope for analyzing the behavior of these categories. Specifically, we observed that fractional derivatives in the current model effectively represent the coexistence dynamics inherent in ecological phenomena.
Using fixed-point theory, we established the existence and uniqueness of solutions and demonstrated Hyers–Ulam stability. Numerical results were graphically represented using the fractional Adams–Bashforth method for iterative solutions, underscoring the significance of the fractional-order derivative. Our findings indicate that as the number of exposed individuals increases, the transmission of addiction also rises, leading to a corresponding increase in the number of depressed individuals.
From an epidemiological perspective, the study shows that reducing and maintaining the reproduction number below one can lead to the eradication of the disease. However, if the reproduction rate reaches one, the disease will persist and continue to spread throughout the population. Future studies can incorporate environmental factors such as seasonality, wealth, interaction rate, age structure, and optimal control.
Author Contributions
Conceptualization, M.S. and S.S.; Methodology, M.S., S.B. and S.S.; Validation, S.B.; Investigation, S.B. and S.S.; Writing—original draft, M.S.; Writing—review & editing, S.B. and S.S.; funding project, S.B.; Supervision, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
The Researchers would like to thank the Deanship of Graduate Studies and Scientific Research at Qassim University for financial support (QU-APC-2025).
Institutional Review Board Statement
This article does not contain any studies with human participants or animals performed by any of the authors.
Data Availability Statement
All data regarding the research work are clearly mentioned in the study.
Acknowledgments
The Researchers would like to thank the Deanship of Graduate Studies and Scientific Research at Qassim University for financial support (QU-APC-2025).
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Ahmad, I.; Ahmad, N.; Shah, K.; Abdeljawad, T. Some appropriate results for the existence theory and numerical solutions of fractals-fractional order malaria disease mathematical model. Results Control. Optim. 2024, 14, 100386. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.J.; Tian, X. Conservation laws for systems of non-standard Birkhoffians with fractional derivatives. Commun. Nonlinear Sci. Numer. Simul. 2024, 130, 107722. [Google Scholar] [CrossRef]
- Singh, J.; Agrawal, R.; Baleanu, D. Dynamical analysis of fractional order biological population model with carrying capacity under Caputo-Katugampola memory. Alex. Eng. J. 2024, 91, 394–402. [Google Scholar] [CrossRef]
- Ismael, M.; Hat, S.; Alabdali, O.; Lone, S.A.; Ali, A.H. Modified optimal auxiliary function method for approximate-analytical solutions in fractional order nonlinear Foam Drainage equations. Partial. Differ. Equ. Appl. Math. 2024, 10, 100700. [Google Scholar] [CrossRef]
- Elsonbaty, A.; Adel, W.; Sabbar, Y.; El-Mesady, A. Nonlinear dynamics and optimal control of a fractional order cotton leaf curl virus model incorporating climate change influences. Partial. Differ. Equ. Appl. Math. 2024, 10, 100727. [Google Scholar] [CrossRef]
- Brahim, M.S.T.; Alloush, T.A.; Cherif, B.B.; Ahmed, A.H. The Study of Asymptotic Behavior of Positive Solutions and its Stability for a New Class of Hyperbolic Differential System. Appl. Math. Inf. Sci. 2019, 13, 341–349. [Google Scholar]
- Shah, K.; Ali, A.; Zeb, S.; Khan, A.; Alqudah, M.A.; Abdeljawad, T. Study of fractional order dynamics of nonlinear mathematical model. Alex. Eng. J. 2022, 61, 11211–11224. [Google Scholar] [CrossRef]
- Eneeva, L.; Pskhu, A.; Rekhviashvili, S. Ordinary differential equation with left and right fractional derivatives and modeling of oscillatory systems. Mathematics 2020, 8, 2122. [Google Scholar] [CrossRef]
- Zitane, H.; Torres, D.F. A class of fractional differential equations via power non-local and non-singular kernels: Existence, uniqueness and numerical approximations. Phys. D Nonlinear Phenom. 2024, 457, 133951. [Google Scholar] [CrossRef]
- Jan, A.; Boulaaras, S.; Abdullah, F.A.; Jan, R. Dynamical analysis, infections in plants, and preventive policies utilizing the theory of fractional calculus. Eur. Phys. J. Spec. Top. 2023, 232, 2497–2512. [Google Scholar] [CrossRef]
- Jan, R.; Boulaaras, S.; Alnegga, M.; Abdullah, F.A. Fractional-calculus analysis of the dynamics of typhoid fever with the effect of vaccination and carriers. Int. J. Numer. Model. Electron. Netw. Devices Fields 2024, 37, e3184. [Google Scholar] [CrossRef]
- Bahi, M.C.; Bahramand, S.; Jan, R.; Boulaaras, S.; Ahmad, H.; Guefaifia, R. Fractional view analysis of sexual transmitted human papilloma virus infection for public health. Sci. Rep. 2024, 14, 3048. [Google Scholar] [CrossRef] [PubMed]
- Saber, H.; Ferhat, M.; Benaissa Cherif, A.; Blouhi, T.; Himadan, A.; Alraqad, T.; Moumen, A. Asymptotic Behavior for a Coupled Petrovsky-Petrovsky System with Infinite Memories. Mathematics 2023, 11, 4457. [Google Scholar] [CrossRef]
- Zaman, U.H.M.; Arefin, M.A.; Akbar, M.A.; Uddin, M.H. Utmost travelling wave phenomena to the fractional type nonlinear evolution equation in mathematical physics. Partial. Differ. Equ. Appl. Math. 2024, 10, 100678. [Google Scholar] [CrossRef]
- Mathiyalagan, K.; Renugadevi, T.V.; Zhang, H.; Shi, Y. Boundary stabilization of semi-linear time fractional reaction-diffusion systems with delays. Asian J. Control 2024, 1–14. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Liu, H. Consensus control of fractional-order systems based on delayed state fractional order derivative. Asian J. Control 2017, 19, 2199–2210. [Google Scholar] [CrossRef]
- Bouafoura, M.K.; Braiek, N.B. A state feedback control design for generalized fractional systems through orthogonal functions: Application to a fractional inverted pendulum. Asian J. Control 2013, 15, 773–782. [Google Scholar] [CrossRef]
- Chen, Q.; Sabir, Z.; Raja, M.A.Z.; Gao, W.; Baskonus, H.M. A fractional study based on the economic and environmental mathematical model. Alex. Eng. J. 2023, 65, 761–770. [Google Scholar] [CrossRef]
- Ganji, R.M.; Jafari, H.; Moshokoa, S.P.; Nkomo, N.S. A mathematical model and numerical solution for brain tumor derived using fractional operator. Results Phys. 2021, 28, 104671. [Google Scholar] [CrossRef]
- Abidemi, A.; Owolabi, K.M. Unravelling the dynamics of Lassa fever transmission with nosocomial infections via non-fractional and fractional mathematical models. Eur. Phys. J. Plus 2024, 139, 1–30. [Google Scholar] [CrossRef]
- Pooseh, S.; Almeida, R.; Torres, D.F.M. Numerical approximations of fractional derivatives with application. Asian J. Control 2013, 15, 698–712. [Google Scholar] [CrossRef]
- Khanra, M.; Pal, J.; Biswas, K. Rational approximation and analog realization of fractional order transfer function with multiple fractional powered terms. Asian J. Control 2012, 15, 723–735. [Google Scholar] [CrossRef]
- Qureshi, S. Real life application of Caputo fractional derivative for measles epidemiological autonomous dynamical system. Chaos Solitons Fractals 2020, 134, 109744. [Google Scholar] [CrossRef]
- Ul Haq, I.; Ali, N.; Bariq, A.; Akgül, A.; Baleanu, D.; Bayram, M. Mathematical modelling of COVID-19 outbreak using Caputo fractional derivative: Stability analysis. Appl. Math. Sci. Eng. 2024, 32, 2326982. [Google Scholar] [CrossRef]
- Ulam, S.M. Problem in Modern Mathematics; John Wiley and Sons: New York, NY, USA, 1964. [Google Scholar]
- Hyers, D.H. On the stability of the linear functional equation. Proc. Natl. Acad. Sci. USA 1941, 27, 222–224. [Google Scholar] [CrossRef]
- Rassias, T.M. On the stability of the linear mappings in Banach Spaces. Proc. Am. Math. Soc. 1978, 72, 297–300. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Tassaddiq, A.; Qureshi, S.; Soomro, A.; Arqub, O.A.; Senol, M. Comparative analysis of classical and Caputo models for COVID-19 spread: Vaccination and stability assessment. Fixed Point Theory Algorithms Sci. Eng. 2024, 2024, 1–23. [Google Scholar] [CrossRef]
- Li, M.; Yang, X.; Song, Q.; Chen, X. Iterative sequential approximate solutions method to Hyers-Ulam stability of time-varying delayed fractional-order neural networks. Neurocomputing 2023, 557, 126727. [Google Scholar] [CrossRef]
- Sher, M.; Shah, K.; Sarwar, M.; Alqudah, M.A.; Abdeljawad, T. Mathematical analysis of fractional order alcoholism model. Alex. Eng. J. 2023, 78, 281–291. [Google Scholar] [CrossRef]
- Matthews, K.; Heravi, S.; Morgan, P.; Page, N.; Shepherd, J.; Sivarajasingam, V. Alcohol prices, the April effect, and the environment, in violence-related injury in England and Wales. Eur. J. Health Econ. 2024, 25, 237–255. [Google Scholar] [CrossRef]
- Suganya, V.; Padmasekaran, S.; Dickson, S. Stability analysis of a dynamic cancer mathematical model with the impact of smoking and alcohol consumption. Bol. Soc. Mat. Mex. 2024, 30, 26. [Google Scholar] [CrossRef]
- Din, A.; Li, Y. The extinction and persistence of a stochastic model of drinking alcohol. Results Phys. 2021, 28, 104649. [Google Scholar] [CrossRef]
- Li, S.; Samreen Ullah, S.; Riaz, M.B.; Awwad, F.A.; Teklu, S.W. Global dynamics and computational modeling approach for analyzing and controlling of alcohol addiction using a novel fractional and fractal-fractional modeling approach. Sci. Rep. 2024, 14, 5065. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).