Abstract
The main goal of this study is to provide new q-Fejer and q-Hermite-Hadamard type integral inequalities for uniformly convex functions and functions whose second quantum derivatives in absolute values are uniformly convex. Two basic inequalities as power mean inequality and Holder’s inequality are used in demonstrations. Some particular functions are chosen to illustrate the investigated results by two examples analyzed and the result obtained have been graphically visualized.
1. Introduction and Preliminaries
Convex functions theory is useful in numerous fields as information theory, optimization and especially inequalities theory. The theory of inequalities contains important applications in applied analysis and in fractional calculus. Inequalities are one of the branches of mathematics that have seen many applications in various researches such as statistics, information theory, approximation of averages.
Integral inequalities, as a main part of mathematical inequalities, can be useful for investigating the qualitative and also quantitative features of integrals. Integral inequalities have applications in fractional calculus being an important tool to predict upper and lower bounds in various sciences like probability theory, interpolation spaces and in information theory.
In numerical integration, new formulas have been developed, and new error bounds have been founded by researchers in mathematical inequalities, especially in the realm of fractional calculus and quantum calculus.
The power of existing fractional integrals and derivatives can not describe specific physical phenomena so new types of fractional operators are introduced to offer new insights into fractional variational problems, and for modeling complex systems.
One of the most important inequality is the Hermite-Hadamard inequality. This inequality, which is one of the convex analysis inequalities, was first introduced and proved by C. Hermite and J. Hadamard [1]. Other important and well-known inequality is the Fejer inequality [2]. This inequality has been obtained in the last decade [3] for various functions [4,5,6] such as M-convex, strongly convex, uniformly convex, etc., and many applications of it have been presented (refer to [7,8]).
Hermite-Hadamard inequality and Fejer inequality are two of the most studied integral inequalities if we consider the property of the convexity of functions.
In the tventielh century, the q-derivative or Jackson derivative was defined by Jackson in the field of combinatorics and q-calculus [9]. In 1966, Al-Salam [10] introduced a q-analogue of the q-fractional integral and q-Riemann-Liouville fractional. In q-calculus, the classical derivative is replaced by the q-difference operator in order to deal with non-differentiable functions (see Almeida [11] and Torres and Cresson al [12]). In 1996 the q-Coulomb problem and q-hydrogen atom were investigated in [13,14,15].
Applications of quantum calculus play significant roles in many branches of mathematics and physics in combinatorics, fractals, special functions, cryptography, computer science, mechanics, therefore the q-calculus can be viewed as a bridge between mathematics and physics. Due to the importance and application of Hermite-Hadamard inequality [16], recently this inequality [17,18,19] has been investigated [20,21,22] in the quantum concept [23,24] for convex functions see [25,26,27]. Hermite-Hadamard type inequalities and Fejer type inequalities have been obtained for Riemann-Liouville fractional integrals [28], for q-calculus [19,24,29,30] for example, and for (p,q)-calculus in [31,32,33] for example. q-estimates of Hermite-Hadamard type of inequalities for twice q-differentiable convex functions were given in [32].
The q-calculus was used for fractional integrals recently. In [34] some trapezoid and midpoint type inequalities have been obtained via fractional
-calculus. In addition, for coordinated convex functions some q-Hermite-Hadamard like inequalities have been obtained in [35,36]. In [37] it was obtained some results on Hermite-Hadamard-Fejer type inequalities for fractional integrals. Further results involving these two inequalities and their applications to fractional integral can be found in [38,39,40,41]. Then in 2017 in [42] have been presented a new Hermite-Hadamard and Hermite-Hadamard-Fejer type inequalities by using the Katugampola fractional integrals. In 2020 in [43] several local fractional integral inequalities which give the bounds for the well-known Hermite-Hadamard-Fejer inequality have been analyzed.
In [44], in 2023, the authors obtained some fractional quantum analogue of Hermite-Hadamard inequalities and in [45], recently several fractional quantum estimates of trapezoid type inequalities by using the preinvexity properties of the functions.
New variants of Hermite-Hadamard inequalities for preinvex interval-valued functions (preinvex FVFS) and Hermite-Hadamard-Fejer type inequalities for generalized interval-valued convex functions were given in [46]. In [19] Alp et al. presented for convex functions a version of q-Hermite-Hadamard type inequality by using the left q-integrals. A similar result was given in [20] for the right q-integrals, which is a version of q-Hermite-Hadamard type inequality for convex functions by using the right q-integrals.
In this article, due to the fact that uniformly convex functions are important functions of convex analysis, Hermite-Hadamard inequality is presented in the quantum concept along with its applications in approximation of averages. Motivated by the research from [16,19,47,48] our goal was to study what would become the Hermite-Hadamard-Fejer and Hermite-Hadamard type inequalities in the case of uniformly convex functions.
The paper has been structured in four sections. In Section 1, it will be briefly resume the notions used here, definitions of different types of convexities, Hermite-Hadamard integral and Fejer inequality and then the basic properties regarding q-calculus. In Section 2, we obtain q-Hermite-Hadamard for uniformly convex functions. In Section 3 we formulate and demonstrate the main results in Theorem 4, Theorem 5, Theorem 6, and Theorem 7. In these theorems are given new q-Fejer and q-H-H type integral inequalities for functions whose the second left and right q-derivatives in absolute value are uniformly convex with modulus
. The main advantage of the newly established inequalities arises from the fact that the concept of uniform convexity it is more general than the concept of convexity or strong convexity, therefore we can regain Hermite-Hadamard and Hermite-Hadamard-Fejer type inequalities given for convex or strongly convex functions. The second advantage is that Theorem 1 can have various refinements for q-calculus and fractional integrals and their combinations. It can be seen that in Theorem 3 in our case appears in left member and also in right member terms that contain the modulus
which doesn’t appear in the corresponding theorem from [19] because there the function is only convex. Two examples are presented for checking the validity of our results.In fact, it was investigated the validity of inequality (3) from Theorem 5 in the particular case of Example 1 and Example 2 when the domain of the function is
and
respectively and the modulus is
. It can be seen that the graphic of the right member(magenta) is above the graphic of the left member(green) for Example 2. We used for Figure 1 the Matlab R2023b software version in the given examples. Then several applications to fractional calculus for Fejer inequality from Theorem 1, Section 1 are presented and an application to arithmetic mean as a special mean it is formulated. In addition, interesting applications to special means of real numbers can be formulated. Section 4 is dedicated to discussion and conclusions.
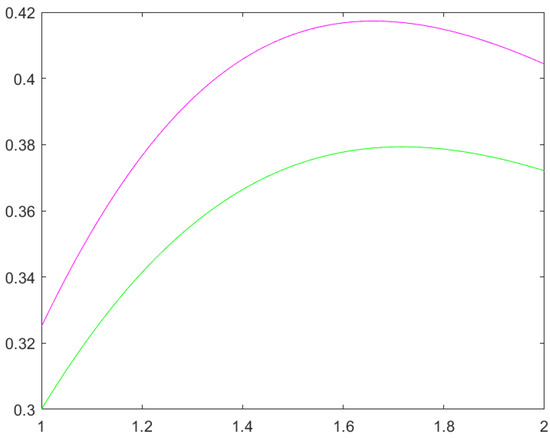
Figure 1.
An example for the inequality (3) from Theorem 5 for function g with uniformly convex right q-derivative of order two,
and
, with modulus
, when
is as in Lemma 1 (b). The magenta line in graphic represents the function of the right member of inequality (3) and the green line represents the function of the left member of inequality (3).
1.1. Convex Functions and Hermite-Hadamard’s Inequality
We recall here three different types of convexities which will be used below in this paper. First, we begin with the definition of the classical convexity, which say that a function
is convex if
for all
and
Definition 1
([4]). “A function
is called strongly convex with modulus
if
holds for all
and
”
The definition of uniformly convex functions with modulus
, can be found in [49].
Definition 2
([49]). “Let
be a function. The function f is called uniformly convex with modulus
if Φ is increasing, vanishes only at 0, and
holds for every
, and
.”
The well-known Hermite-Hadamard’s inequality can be stated as “if
is a convex function, then the following inequality holds:
and when f is a concave function, then previous inequality holds but in the opposite direction” [1]. This inequality is known also as trapezium inequality. A new Fejer type inequality and some new classes of uniformly convex functions given in [48], are two important tools for the results obtained in Section 3 and will be recalled below.
Theorem 1
(Fejer type inequality [48]). “Let f be a uniformly convex function with modulus Φ on
Then we have
where
is integrable function and symmetric with respect to
”
Remark 1.
If we set
in Theorem 1, we get the classical inequality of Hermite-Hadamard for uniformly convex functions as follows:
Lemma 1
([48]). Suppose that
is defined by
(a) If n is an even natural number and
, then
is uniformly convex with modulus
(b) If
then
is uniformly convex with modulus
1.2. Preliminaries on q-Calculus
Let
be a real interval,
and
The q-number is defined for any number n,
.
Several basic definitions, remarks and lemmas of the q-calculus will be presented because they will be used in next section of this paper. We start with definition of right q-derivative of a function.
Definition 3
([20,23]). “The right or
-derivative of
at
is expressed as:
Noe we restate the definition of the left q-derivative of a function [23].
Definition 4
([18,23]). “The left or
-derivative of
at
is expressed as:
Definition 5
([20,23]). “The right or
-integral of
at
is defined as:
Definition 6
([23,25]). “The left or
-integral of
at
is defined as:
Definition 7
([23]). “We have the equality for
- integrals
for
”
For the fundamental properties of these q-derivatives and q-integrals, see for example, [18,26,27]. Recently, new refinements and generalizations of q-Hermite-Hadamard integral inequalities for q-differentiable functions [19,20,21] were given in papers like [22,23,24].
The following two results from
-calculus will be used in calculus of q-left and q-right integrals in Section 3 when
.
Definition 8
([16]). “We have the following equalities
for
”
Lemma 2
([16]). “Consider a mapping
which is twice
-differentiable and
is a continuous and integrable on I. Then the following equality holds:
where
”
We say that a function f defined on I has support at
with modulus
if there exists an affine function
such that
for every
. The graph of the support function f is called a line of support for f at
.
Theorem 2
([49]). “Let
be a function.
- If is uniformly convex with modulus ϕ on , then there is at least one line of support with modulus ϕ for f at each .
- If there is at least one line of support with modulus ϕ for f at each , and , for every and , then f is uniformly convex with modulus ϕ on .”
2. Main Result
In this section we give Hermite-Hadamard inequality for uniformly convex functions for q-calculus.
2.1. q-Hermite-Hadamard Inequality for Uniformly Convex Function
Theorem 3.
Let
be a uniformly convex function with modulus ϕ on
and
. Then we have
Proof.
Since f is uniformly convex with modulus of
, then we have
for every
. By q-integrating on
with respect t we obtain
Hence,
Now, by using Definition 6 we have
Also, we obtain
Finally, by using Definition 6 we get
Proof of other inequality: Since f is uniformly convex, by using Theorem 2 with
, we have
By q-integrate on
we conclude that
Thus
So, we have
hence
□
Remark 2.
If we set
in Theorem 3, we get right of the classical inequality of Hermite-Hadamard as follows:
Proposition 1
([50]). Let
be proper and convex, with exact modulus of convexity ϕ. Then
,
,
and ϕ is increasing.
Remark 3.
In Proposition 1, with
we have
.
Remark 4.
In view of Remark 3, if we set
in Theorem 3, we get left of the classical inequality of Hermite-Hadamard as follows:
Note that this lower bound for uniformly convex functions is better than lower bound in [5].
2.2. q-Fejer Inequality for Uniformly Convex Function
A new Fejer-type q-inequality for uniformly convex functions is presented in this section and then some new q-Hermite-Hadamard type integral inequalities for twice q-differentiable uniformly convex functions, having as a starting point the results formulated in [16,48] are given. In addition, two examples are presented in order to check the established results.
Theorem 4.
Let
be a uniformly convex function with modulus Φ on
If
are q-integrable functions with
symmetric with respect to
then we have,
Proof.
We take
in Definition 2 relation (1) and then as in [48], replacing x by
and y by
we obtain:
Now multiplying previous inequalities by
and q-integrating the obtained inequality with respect to t over
, we find,
By Definition 5 we can see that
and
For
we see that
and using that g is symmetric with respect to
we have by Definition 6
Taking into account that
we can write
Last integral,
will be,
First we compute
thus:
and then
is
□
Theorem 5.
If
is a twice
- differentiable function on
so that
and integrable on
, and if
is uniformly convex with modulus
on
then we have,
Proof.
By using modulus on Lemma 2 [16], and then the definition of uniform convexity with modulus for
it will be obtained:
By calculus we get the desired inequality. □
Example 1.
For the function
defined by
it can be seen that
is strongly convex with modulus
, (i.e.
), see Example 2.2 from [7]. Thus the hypothesys of Theorem 5 are satisfied and the inequality (3) holds. For the calculus of
it was used Definition 3.
Then we get,
The right member becomes
That means we need to check that
or equivalent,
which is obvious because
Example 2.
We consider the function
defined by
. By calculus, using the Definition 3 we obtain
. Now using the Lemma 1, (b) we obtain
Thus g is uniformly convex function with modulus Φ,
and then the conditions of Theorem 5 are satisfied. The inequality (3) becomes:
Again the right member becomes,
For the left member we first compute,
and then we get,
The magenta line in Figure 1 represents the function of the right member of inequality (3) and the green line represents the function of the left member of inequality (3).
Theorem 6.
If
is a twice
-differentiable function on
so that
and integrable on
, and if
,
is uniformly convex with modulus
on
then we have,
Proof.
By using the modulus properties in Lemma 2 [16], and the q-power mean inequality, we have,
Then by definition of uniform convexity with modulus
for the function
, we find
□
Theorem 7.
Let
be a twice
- differentiable function on
so that
and integrable on
. If
is uniformly convex with modulus
on
, for some
and
then the following inequality holds:
where
Proof.
By using the modulus properties in Lemma 2 [16], and the well-known q-Holder’s inequality we have,
By using the hypothesis that
is uniformly convex with modulus
on
it will be obtained
which leads to desired results. □
3. Applications to Fractional Calculus
In this section, an application to the fractional calculus of the Fejer inequality given in [48] is presented. First, it is necessary to recall the definition of the classical Riemann–Liouville fractional integrals.
Definition 9.
“Let
. The Riemann–Liouville fractional integrals
and
of order
, with
, are defined as follows:
and
respectively, where Γ is the well-known gamma function.”
Theorem 8.
Let
and f be a uniformly convex function with modulus Φ on
Then we have,
where
is symmetric function with respect to
Proof.
We use the same method as in the demonstration of Theorem 1. We take
in Definition 2 relation (1) and then replacing x by
and y by
we get:
Now multiplying previous inequalities by
and integrating the obtained inequality with respect to t over
, we find,
By calculus, we have
where
, and
For next integral,
, it will be used the symmetry of g with respect to
and that
, obtaining
Using again that
, in
, we have,
The integral, G is the expression,
which will be written:
where
when
and
when
. □
Theorem 9.
Let
and f be a uniformly convex function with modulus Φ on
Then we have,
where
is symmetric function with respect to
Proof.
We use the same method as in the demonstration of Theorem 1. □
Combining the inequalities from Theorem 8 and Theorem 9, we find the following companion like inequality:
Remark 5.
Let
, f be a uniformly convex function with modulus Φ on
and
is a symmetric function with respect to
Then the following inequality holds:
Proof.
It will be used last two inequalities from Theorem 8 and Theorem 9. □
Remark 6.
If we take
and
in equality from Lemma 2, [47] then this inequality can be rewritten as follows:
Theorem 10.
If the hypothesis of previous remark take place and
is uniformly convex with modulus Φ, then the following inequality holds:
Proof.
The modulus property in the identity from Lemma 2 is used, and we get
and by calculus, we obtain the desired inequality. □
As application to special means, in fact an application to arithmetic mean, it will be presented below, rewriting Theorem 10.
Remark 7.
If the hypothesis of previous remark take place and
is uniformly convex with modulus Φ, then next inequality is true:
where
is the arithmetic mean of the real numbers a and b.
If, in addition, we particularize the function f from previous remark, then new means inequalities could be also obtained.
4. Discussion and Conclusions
The main findings of this paper are designed to give new refinements of q-Hermite-Hadamard-Fejer inequality and of q-Hermite-Hadamard-type integral inequalities for functions whose second left and right q-derivatives are uniformly convex. Basic inequalities such as q-Holder’s integral inequality and q-power mean inequality have been used to establish the new estimated bounds. We used the Matlab R2023b software version for Figure 1 and for some calculus in the given examples. The examples presented illustrate the validity of the given results. Applications of the Fejer inequality from Theorem 1 are given for uniformly convex functions with modulus
on
in the case of Riemann-Liouville fractional integrals. Many interesting consequences and applications to special means can be formulated. An application to arithmetic mean as a special mean of real numbers it is presented.There are two important advantages of the newly established results derived from the fact that we used uniformly convex functions which are more general than convex or strongly convex functions, and the second advantage is that the Theorem 1 supports various kind of generalizations for q-calculus, parametrized quantum integral calculus,
-calculus, fractional calculus and q-fractional calculus.
Therefore, it is interesting to extend such findings to other new kinds of convexities,
-calculus, q-fractional inequalities. We hope that these results will enrich the literature in the field.
Author Contributions
Conceptualization, H.B., S.M., Y.S. and L.C.; methodology, H.B., S.M., Y.S. and L.C.; software, H.B., S.M., Y.S. and L.C.; validation, H.B. and L.C.; formal analysis, S.M., Y.S. and L.C.; investigation, H.B.; resources, L.C.; data curation, H.B.; writing—original draft preparation, H.B. and L.C.; writing—review and editing, H.B. and L.C.; visualization, H.B., S.M., Y.S. and L.C.; supervision, H.B., S.M., Y.S. and L.C.; project administration, H.B. and L.C.; funding acquisition, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hadamard, J. Etude sur les proprietes des fonctions entieres en particulier d’une fonction consideree par Riemann. J. Math. Pures Appl. 1893, 58, 171–215. [Google Scholar]
- Fejer, L. Uber die Fourierreihen, II. Math. Naturwiss. Anz. Ungar. Akad. Wiss. 1906, 24, 369–390. (In Hungarian) [Google Scholar]
- Barsam, H.; Sayyari, Y. On some inequalities of differentable uniformly convex mapping with applications. Numer. Funct. Anal. Optim. 2023, 44, 368–381. [Google Scholar] [CrossRef]
- Khan, M.A.; Anwar, S.; Khalid, S.; Sayed, Z.M.M.M. Inequalities of the type Hermite-Hadamard-Jensen-Mercer for strong convexity. Math. Probl. Eng. 2021, 2021, 5386488. [Google Scholar]
- Niezgoda, M. Fejer and Hermite-Hadamard type results for H-invex functions with applications. Positivity 2019, 23, 531–543. [Google Scholar] [CrossRef]
- Sayyari, Y. New Entropy Bounds Via Uniformly Convex Functions. Chaos Solitons Fractals 2020, 141, 110360. [Google Scholar] [CrossRef]
- Sayyari, Y.; Barsam, H.; Ciurdariu, L. A new refinement of Jensen-Type inequality with respect to uniformly convex functions with applications in information theory. J. Math. Inequal. 2023, 17, 1311–1322. [Google Scholar] [CrossRef]
- Sayyari, Y.; Barsam, H. New inequalities related to entropy and relative entropy with respect to Hermite-Hadamard inequality. Filomat 2024, 38, 1265–1277. [Google Scholar] [CrossRef]
- Jackson, F.H. On a q-definite integrals. Q. J. Pure Appl. Math. 1910, 41, 193–203. [Google Scholar]
- Al-Salam, W. Some fractional q-integrals and q-derivatives. Proc. Edinb. Math. Soc. 1966, 15, 135–140. [Google Scholar] [CrossRef]
- Almeida, R.; Torres, D.F.M. Non-differentiable variational principles in terms of a quantum operator. Math. Methods Appl. Sci. 2011, 34, 2231–2241. [Google Scholar]
- Cresson, J.; Frederico, G.S.F.; Torres, D.F.M. Constants of motion for non-differentiable quantum variational problems. Topol. Methods Nonlinear Anal. 2019, 37, 217–231. [Google Scholar] [CrossRef]
- Chen, F.L.; Finkelstein, R.J. q-deformation of the Coulomb problem. J. Math. Phys. 1994, 35, 3273–3284. [Google Scholar] [CrossRef]
- Cadavid, A.C.; Finkelstein, R.J. The q-Coulomb problem in configuration space. J. Math. Phys. 1996, 37, 3675–3683. [Google Scholar] [CrossRef]
- Finkelstein, R.J. The q-Coulomb problem. J. Math. Phys. 1996, 37, 2628–2636. [Google Scholar] [CrossRef]
- Sitthiwirattham, T.; Murtaza, G.; Ali, M.A.; Ntouyas, S.K.; Adeel, M.; Soontharanon, J. On some new trapezoidal type inequalities for twice (p,q) differentiable convex functions in post quantum calculus. Symmetry 2021, 13, 1605. [Google Scholar] [CrossRef]
- Tariboon, J.; Ntouyas, S.K. Quantum calculus on finite intervals and aplications to impulsive difference equations. Adv. Differ. Equ. 2013, 2013, 282. [Google Scholar] [CrossRef]
- Tariboon, J.; Ntouyas, S.K. Quantum integral inequalities on finite intervals. J. Inequal. Appl. 2014, 13, 121. [Google Scholar] [CrossRef]
- Alp, N.; Sarikaya, M.Z.; Kunt, M.; Iscan, I. q2-Hermite-Hadamard inequalities and quantum estimates for midpoint type inequalities via convex and quasi-convex functions. J. King Saud Univ. Sci. 2018, 30, 193–203. [Google Scholar] [CrossRef]
- Bermudo, S.; Korus, P.; Valdes, J.N. On q-Hermite-Hadamard inequalities for general convex functions. Acta Math. Hungar. 2020, 162, 364–374. [Google Scholar] [CrossRef]
- Kara, H.; Budak, H.; Alp, N.; Kalsoom, H.; Sarikaya, M.Z. On new generalized quantum integrals and related Hermite-Hadamard inequalities. J. Inequal. Appl. 2021, 2021, 180. [Google Scholar] [CrossRef]
- Jhanthanam, S.; Tariboon, J.; Ntouyas, S.K.; Nonlaopon, K. On q-Hermite-Hadamard inequalities for differentiable convex functions. Mathematics 2019, 7, 632. [Google Scholar] [CrossRef]
- Alp, N.; Budak, H.; Sarikaya, M.Z.; Ali, M.A. On new refinements and generalizations of q-Hermite-Hadamard inequalities for convex functions. Rocky Mt. J. Math. 2023, 54, 361–374. [Google Scholar] [CrossRef]
- Zhao, D.; Ali, M.A.; Luangboon, W.; Budak, H.; Nonlaopon, K. Some Generalizations of Different Types of Quantum Integral Inequalities for Differentiable Convex Functions with Applications. Fractal Fract. 2022, 6, 129. [Google Scholar] [CrossRef]
- Rajkovic, P.M.; Stankovic, M.S.; Marinkovic, S.D. The zeros of polynomials orthogonal with respect to q-integral on several intervals in the complex plane. In Proceedings of the Fifth International Conference of Geometry Integrability and Quantization, Varna, Bulgaria, 5–12 June 2003; pp. 178–188. [Google Scholar]
- Ernst, T.A. Comprehensive Treatment of q-Calculus; Springer: Basel, Switzerland, 2012. [Google Scholar]
- Kac, V.; Cheung, P. Quantum Calculus; Springer: New York, NY, USA, 2003; p. 652. [Google Scholar]
- Kang, Q.; Butt, S.I.; Nazeer, W.; Nadeem, M.; Nasir, J.; Yang, H. New variant of Hermite-Hadamard-Mercer inequalities via Riemann-Liouville fractional integral operators. J. Math. 2020, 2020, 4303727. [Google Scholar] [CrossRef]
- Kunt, M.; Iscan, I.; Alp, N.; Sarikaya, M.Z. (p,q)-Hermite-Hadamard inequalities and (p,q)-estimations for midpoint type inequalities via convex and quasi-convex functions. Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. 2018, 112, 969–992. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Awan, M.U.; Talib, S.; Kashuri, A.; Noor, M.A. Some new post-quantum integral inequalities involving twice (p,q)-differentiable ϕ-preinvex functions and applications. Axioms 2021, 10, 283. [Google Scholar] [CrossRef]
- Noor, M.; Noor, K.; Awan, M. Quantum Ostrowski inequalities for q-differentiable convex functions. J. Math. Inequal. 2016, 10, 1013–1018. [Google Scholar] [CrossRef]
- Liu, W.; Zhuang, H. Some quantum estimates of Hermite-Hadamard inequalities for convex functions. J. Appl. Anal. Comput. 2016, 7, 501–522. [Google Scholar]
- Vivas-Cortez, M.; Kashuri, A.; Liko, R.; Hernadez, J.E. Quantum trapezium-type inequalities using generalized Φ-convex functions. Axioms 2020, 9, 12. [Google Scholar] [CrossRef]
- Neang, P.; Nanlaopon, K.; Tariboon, J.; Ntouyas, S.K.; Aagarwal, P. Some trapezoid and midpoint type inequalities via fractional (p,q)-calculus. Adv. Differ. Equ. 2021, 2021, 333. [Google Scholar] [CrossRef]
- Budak, H.; Ali, M.A.; Tarhanaci, M. Some new quantum Hermite-Hadamard-like inequalities for coordinated convex functions. J. Optim. Theory Appl. 2020, 186, 899–910. [Google Scholar] [CrossRef]
- Kunt, M.; Latif, M.A.; Iscan, I.; Dragomir, S.S. Quantum Hermite-Hadamard type inequality and some estimates of quantum midpoint type inequalities for double integrals. Sigma J. Eng. Nat. Sci. 2019, 37, 207–223. [Google Scholar]
- Iscan, I. Hermite-Hadamard-Fejertype inequalities for convex functions via fractional integrals. arXiv 2014, arXiv:1404.7722. [Google Scholar]
- Chen, F. Extensions of the Hermite-Hadamard inequality for harmonically convex functions via fractional integrals. Appl. Math. Comput. 2015, 268, 121–128. [Google Scholar] [CrossRef]
- Iscan, I.; Wu, S. Hermite-Hadamard type inequalities for harmonically convex functions via fractional integrals. Appl. Math. Comput. 2014, 238, 237–244. [Google Scholar]
- Set, E.; Iscan, I.; Sarikaja, M.Z.; Ozdemir, M.E. On new inequalities of Hermite-Hadamad-Fejer type for convex functions via fractional integrals. Appl. Math. Comput. 2015, 259, 875–881. [Google Scholar]
- Almeida, R.; Bastos, N. An approximation formula for the Katugampola integral. J. Math. Anal. 2016, 7, 23–30. [Google Scholar]
- Chen, H.; Katugampola, U.N. Hermite-Hadamard and Hermite-Hadamard-Fejer type inequalities for generalized fractional integrals. J. Math. Anal. Appl. 2017, 446, 1274–1291. [Google Scholar] [CrossRef]
- Luo, C.; Wang, H.; Du, T. Fejer-Hermite-Hadamard type inequalities involving generalized h-convexity on fractal sets and their applications. Chaos Solitons Fractals 2020, 131, 109547. [Google Scholar] [CrossRef]
- Kunt, M.; Aljasem, M. Fractional quantum Hermite-Hadamard type inequalities. Konuralp J. Math. 2020, 8, 122–136. [Google Scholar]
- Chu, Y.M.; Awan, M.U.; Talib, S.; Noor, M.A.; Noor, K.I. Fractional quantum analogues of trapezoid like inequalities. J. Math. Inequal. 2023, 17, 31–47. [Google Scholar] [CrossRef]
- Khan, M.B.; Marcias-Dias, J.E.; Treanta, S.; Soliman, M.S. Some Fejer type inequalities for Generalized Interval-Valued Convex functions. Mathematics 2022, 10, 385. [Google Scholar] [CrossRef]
- Ciurdariu, L.; Grecu, E. Hermite-Hadamard-Mercer-Type Inequalities for Three-Times Differentiable Functions. Axioms 2024, 13, 413. [Google Scholar] [CrossRef]
- Barsam, H.; Sayyari, Y. Fejer type inequality and some inequalities of Hermite-Hadamard type via uniformly convex function. submitted.
- Zalinescu, C. On uniformly convex functions. J. Math. Anal. Appl. 1983, 95, 344–374. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).