Direct Synthesis of Fractional-Order Controllers Using Only Two Design Equations with Robustness to Parametric Uncertainties
Abstract
1. Introduction
2. Theoretical Background
2.1. Second-Order Canonical Transfer Function
2.2. Fractional Calculus
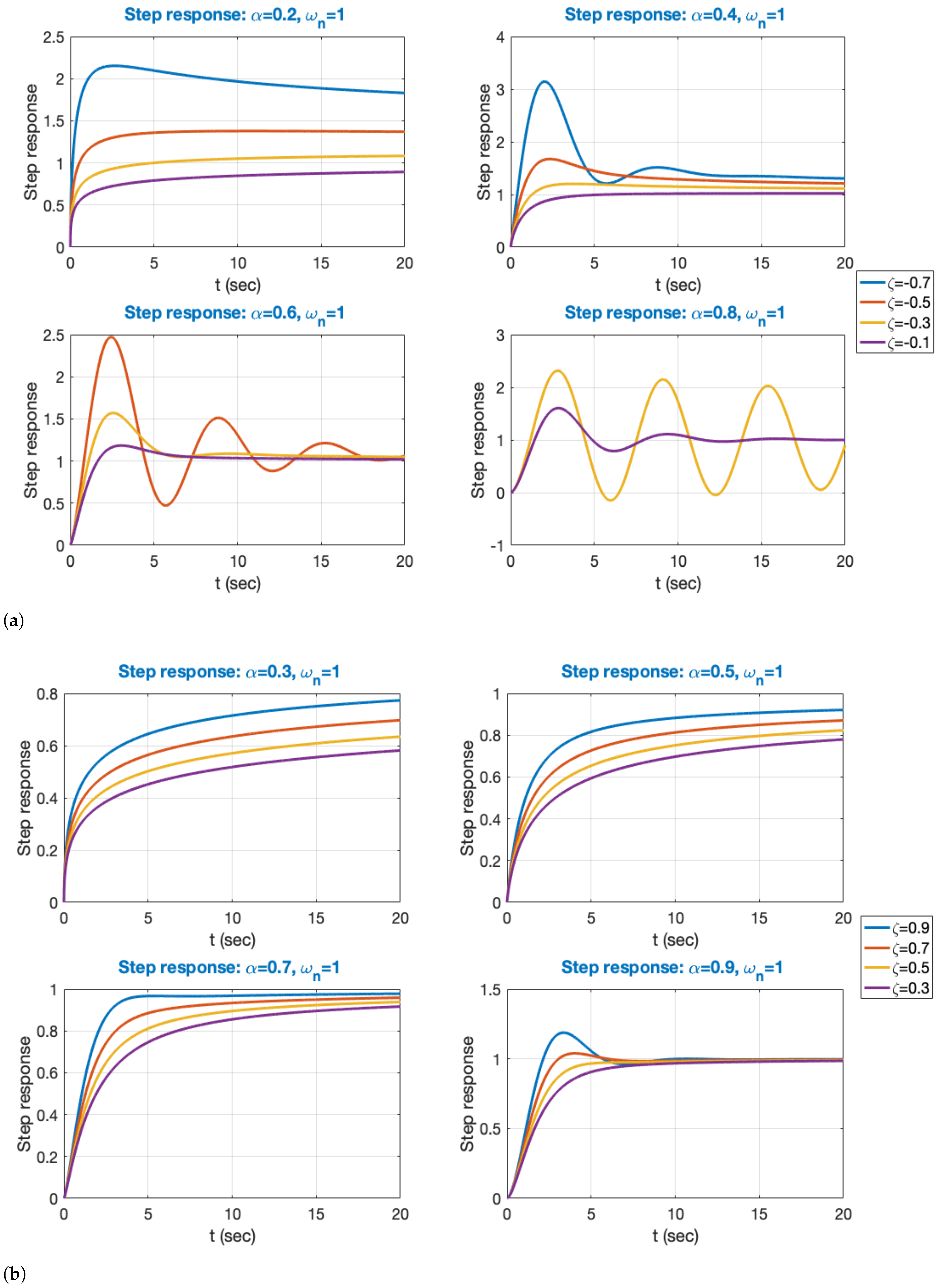
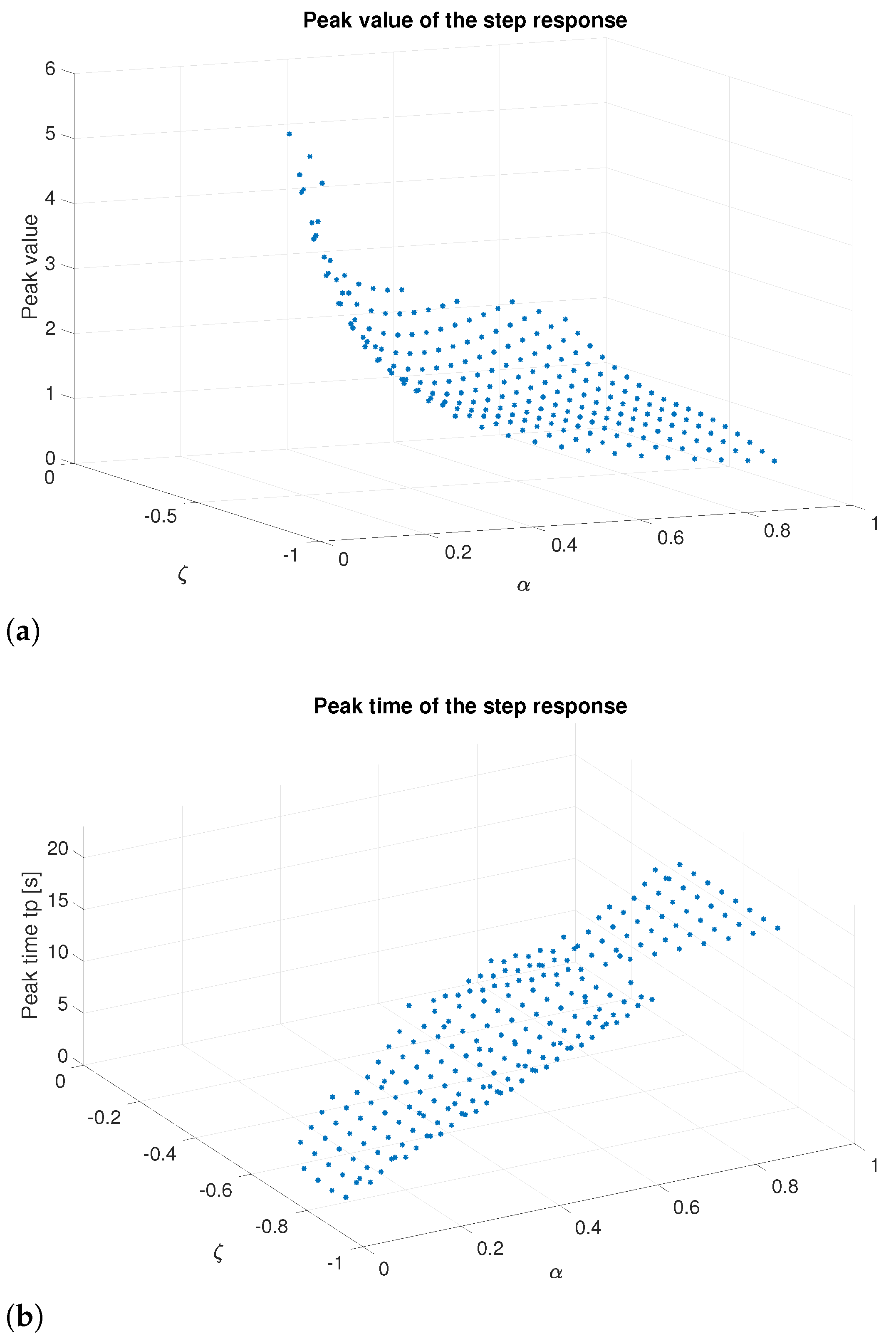
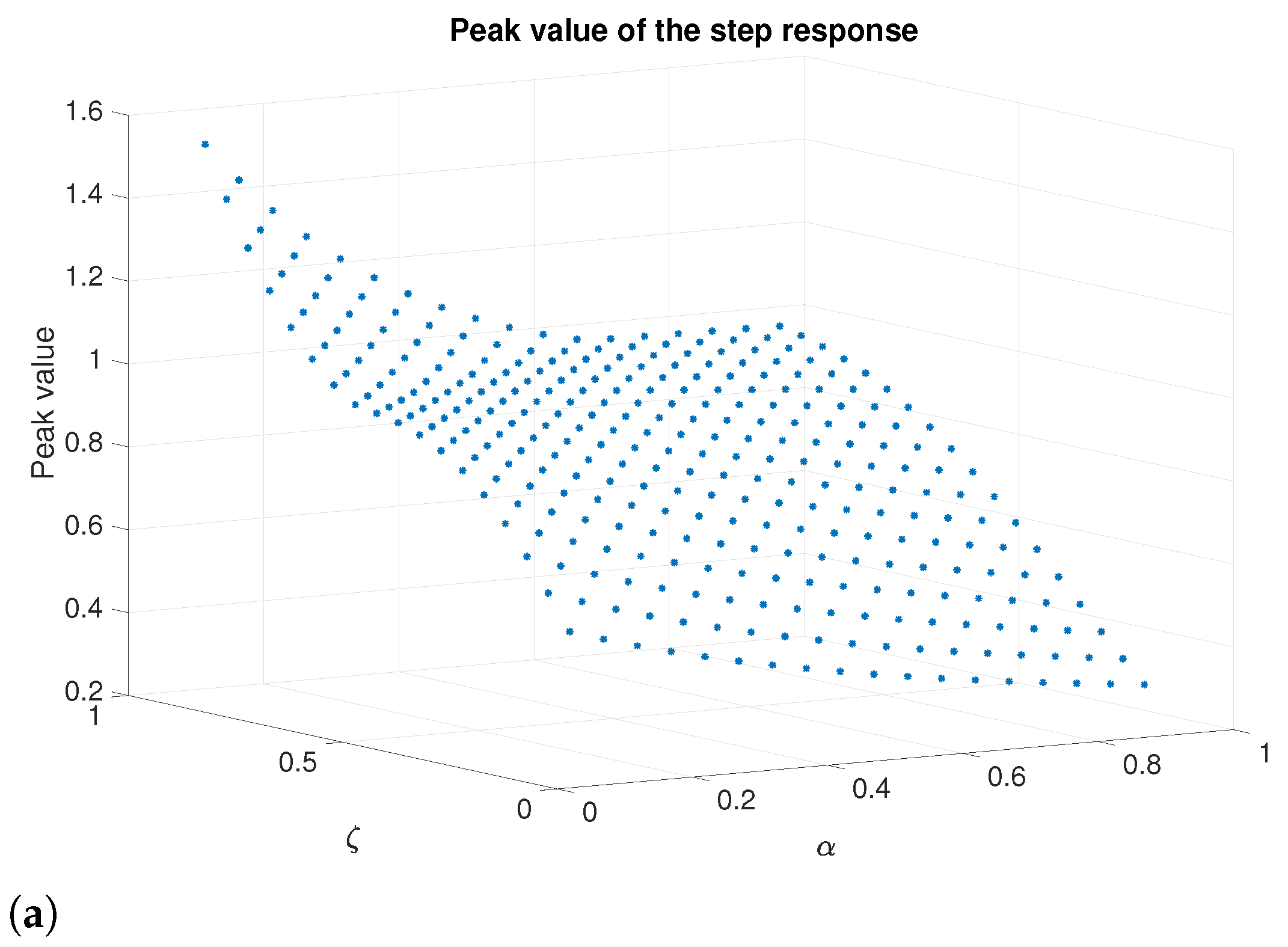
2.3. Three-Term Fractional-Order Canonical Form
2.4. Controllers
2.4.1. Integer-Order Phase Lead/Lag Compensator
2.4.2. Fractional-Order PID Controller
2.4.3. Fractional-Order ID Controller
2.4.4. Fractional-Order Direct Synthesis Control
2.5. Performance Metrics and Statistical Analysis
2.5.1. Integrated Square Error (ISE)
2.5.2. Integral Square Control Error Performance Index (ISCE)
2.5.3. Monte Carlo Analysis
- % MonteCarlo Analysis
- % Parameter variations and normal distribution
- Kp = 1; % nominal gain
- N = 400; % number of cases
- des = 0.25; % 25% std deviation
- % Gain variation
- Kp_mc = normrnd(Kp, des∗Kp).
2.5.4. Lilliefors Normality Test
2.5.5. Levene’s Test
2.5.6. Kruskal–Wallis Test
3. Proposed Method
3.1. Stability Analysis
3.2. Phase Margin
3.3. Disturbance Response
3.4. Gain Margin
3.5. Implementation Steps
4. Example
4.1. Utilization of the Method
4.2. Direct Synthesis
5. Evaluation of the Proposed Method Based on Simulations Results
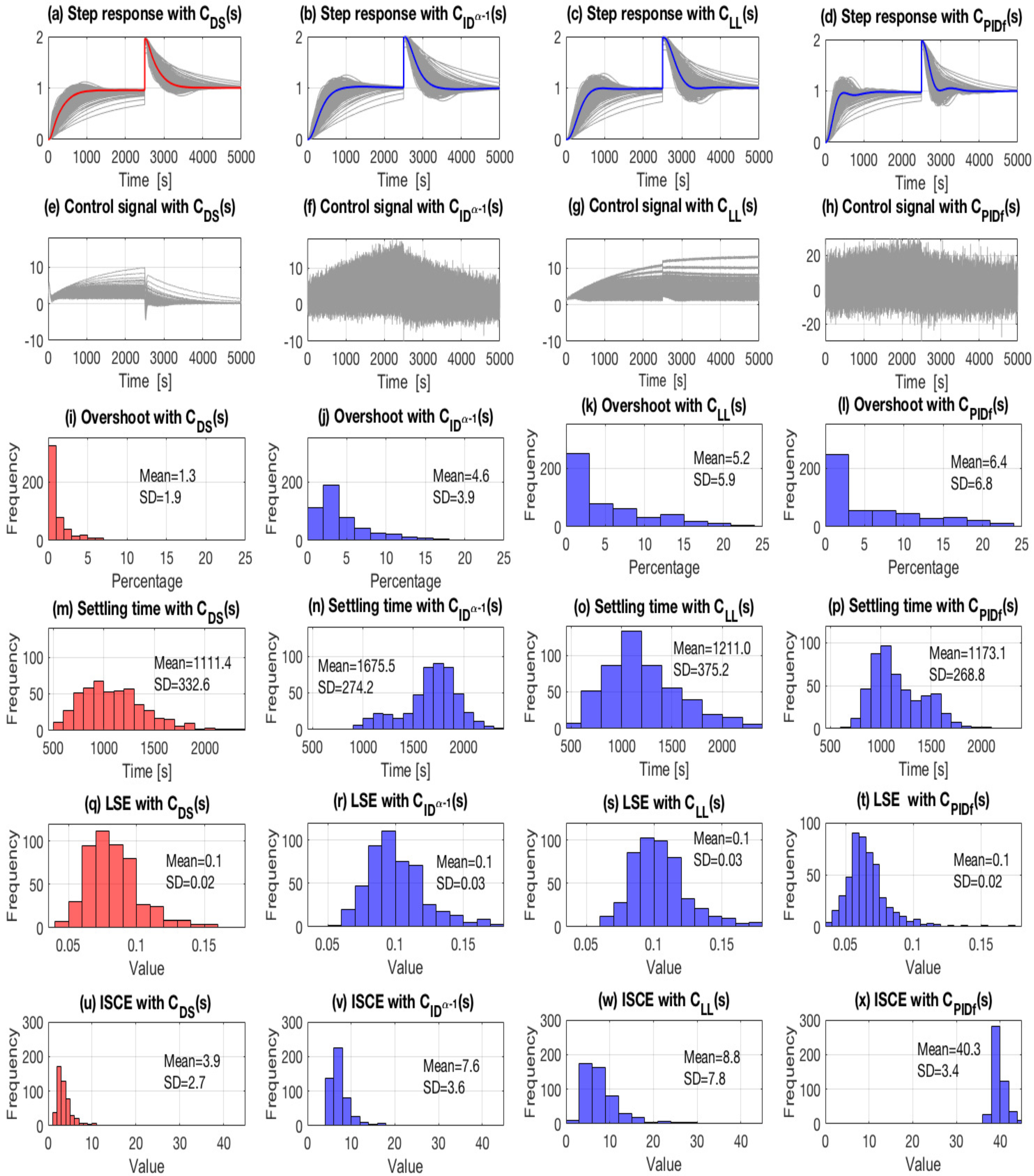
5.1. Scenario Without Parameter Variations
5.2. Scenario with Parameter Variations: Monte Carlo Analysis
5.3. Inferential Statistical Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FOC | Fractional-Order Controller |
| IOC | Integer-Order Controller |
| FOPID | Fractional-Order PID Controller |
| FOID | Fractional-Order ID Controller |
| DS | Direct Synthesis |
| FO-DS | Fractional-order Direct Synthesis |
| Integrated square error | |
| Normalized ISE | |
| Integrated square control and error index | |
| Normalized ISCE | |
| IMC | Internal Model Controller |
| , | Reference signal (setup) |
| , | Noise signal |
| Error signal | |
| Control signal | |
| Controlled signal | |
| System transfer function (process) | |
| Closed-loop transfer function | |
| Loop gain | |
| Fractional-order closed-loop transfer function | |
| Direct synthesis controller | |
| Fractional-order ID controller | |
| Lead-lag phase compensator | |
| Fractional-order PID controller | |
| Integer-order damping factor | |
| Fractional-order damping factor | |
| Overshoot | |
| Settling time to 2% | |
| Phase crossover frequency | |
| Steady-state error | |
| Integer-order gain crossover frequency | |
| Fractional-order natural frequency | |
| Loop gain | |
| Phase margin | |
| Gain margin | |
| Disturbances bandwidth | |
| A | Gain at in dB |
| Fractional order of | |
| , | Fractional orders of |
| N | Number of Monte Carlo runs |
| n | Number of terms in the integer-order approximation |
References
- Oustaloup, A.; Melchior, P. The great principles of the Crone control. In Proceedings of the IEEE Systems Man and Cybernetics Conference—SMC, Le Touquet, France, 17–20 October 1993; Volume 2, pp. 118–129. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-Order Systems and Fractional-Order Controllers; Institute of Experimental Physics, Slovak Academy of Sciences: Kosice, Slovakia, 1994; Volume 12, pp. 1–18. Available online: https://igor.podlubny.website.tuke.sk/pspdf/uef0394.pdf (accessed on 1 November 2024).
- Pérez, R.R.; García, F.C.; Moriano, J.S.; Batlle, V.F. Control robusto de orden fraccionario de la presión del vapor en el domo superior de una caldera bagacera. Rev. Iberoam. Autom. Inform. Ind. 2014, 11, 20–31. [Google Scholar] [CrossRef]
- Memlikai, E.; Kapoulea, S.; Psychalinos, C.; Baranowski, J.; Bauer, W.; Tutaj, A.; Piatek, P. Design of fractional-order lead compensator for a car suspension system based on curve-fitting approximation. Fractal Fract. 2021, 5, 46. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Moore, K.L.; Vinagre, B.M.; Podlubny, I. Robust PID controller autotuning with an isodamping property through a phase shaper. In Fractional Differentiation and Its Applications; Ubooks Verlag: Mossautal, Germany, 2005; pp. 687–706. [Google Scholar]
- Monje, C.A.; Vinagre, B.M.; Feliu, V.; Chen, Y. Tuning and auto-tuning of fractional order controllers for industry applications. Control. Eng. Pract. 2008, 16, 798–812. [Google Scholar] [CrossRef]
- Fergani, N. Direct synthesis-based fractional-order PID controller design: Application to AVR system. Int. J. Dyn. Control 2022, 10, 2124–2138. [Google Scholar] [CrossRef]
- Muresan, C.I.; Keyser, R.D. Revisiting Ziegler–Nichols: A fractional order approach. ISA Trans. 2022, 129, 287–296. [Google Scholar] [CrossRef] [PubMed]
- Saleem, O.; Ali, S.; Iqbal, J. Robust MPPT control of stand-alone photovoltaic systems via adaptive self-adjusting fractional-order PID controller. Energies 2023, 16, 5039. [Google Scholar] [CrossRef]
- Ghamari, S.M.; Jouybari, T.Y.; Mollaee, H.; Khavari, F.; Hajihosseini, M. Design of a novel robust adaptive cascade controller for DC-DC buck-boost converter optimized with neural network and fractional-order PID strategies. J. Eng. 2023, 2023, 12244. [Google Scholar] [CrossRef]
- Trivedi, R.; Verma, B.; Padhy, P. Indirect optimal tuning rules for fractional-order proportional integral derivative controller. Int. J. Numer. Model. Electron. Netw. 2020, 34, e2838. [Google Scholar] [CrossRef]
- Nassef, A.M.; Abdelkareem, M.A.; Maghrabie, H.M.; Baroutaji, A. Metaheuristic-based algorithms for optimizing fractional-order controllers—A recent, systematic, and comprehensive review. Fractal Fract. 2023, 7, 553. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Advances in Industrial Control; Springer: London, UK, 2010. [Google Scholar]
- Chen, Y.; Petras, I.; Xue, D. Fractional order control - a tutorial. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 1397–1411. [Google Scholar] [CrossRef]
- Das, S.; Saha, S.; Das, S.; Gupta, A. On the selection of tuning methodology of FOPID controllers for the control of higher order processes. ISA Trans. 2011, 50, 376–388. [Google Scholar] [CrossRef]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Muñiz-Montero, C.; García-Jiménez, L.V.; Sánchez-Gaspariano, L.A.; Sánchez-López, C.; González-Díaz, V.R.; Tlelo-Cuautle, E. New alternatives for analog implementation of fractional-order integrators, differentiators and PID controllers based on integer-order integrators. Nonlinear Dyn. 2017, 90, 241–256. [Google Scholar] [CrossRef]
- Nie, Z.; Zheng, Y.; Wang, Q.G.; Liu, R.; Xiang, L.J. Fractional-order PID controller design for time-delay systems based on modified Bode’s ideal transfer function. IEEE Access 2020, 8, 103500–103510. [Google Scholar] [CrossRef]
- Soukkou, A.; Belhour, M.C.; Leulmi, S. Review, design, optimization and stability analysis of fractional-order PID controller. Int. J. Intell. Syst. Appl. 2016, 8, 73. [Google Scholar] [CrossRef]
- Laifa, S.; Boudjehem, B.; Gasmi, H. Direct synthesis approach to design fractional PID controller for SISO and MIMO systems based on Smith predictor structure applied for time-delay non-integer-order models. Int. J. Dyn. Control 2022, 10, 760–770. [Google Scholar] [CrossRef]
- Kumar, A.; Pan, S. Design of fractional-order PID controller for load frequency control system with communication delay. ISA Trans. 2022, 129, 138–149. [Google Scholar] [CrossRef]
- Ahmed, S. Fractional-order controller design using the direct synthesis method. In Proceedings of the 2022 IEEE International Symposium on Advanced Control of Industrial Processes (AdCONIP), Vancouver, BC, Canada, 7–9 August 2022; pp. 337–342. [Google Scholar] [CrossRef]
- Arya, P.P.; Chakrabarty, S. A robust internal model-based fractional-order controller for fractional-order plus time delay processes. IEEE Control Syst. Lett. 2020, 4, 862–867. [Google Scholar] [CrossRef]
- Yumuk, E.; Güzelkaya, M.; Eksin, I. Optimal fractional-order controller design using direct synthesis method. IET Control Theory Appl. 2020, 14, 2960–2967. [Google Scholar] [CrossRef]
- Vavilala, S.K.; Thirumavalavan, V. Analytical design of the fractional order controller and robustness verification. IAES Int. J. Robot. Autom. (IJRA) 2021, 10, 10–23. [Google Scholar] [CrossRef]
- Icmez, Y.; Can, M.S. Smith predictor controller design using the direct synthesis method for unstable second-order and time-delay systems. Processes 2023, 11, 941. [Google Scholar] [CrossRef]
- Ajmeri, M.; Ali, A. Analytical design of modified Smith predictor for unstable second-order processes with time delay. Int. J. Syst. Sci. 2017, 48, 1671–1681. [Google Scholar] [CrossRef]
- Nise, N.S. Control Systems Engineering, 6th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Thammarat, C.; Puangdownreong, D. CS-based optimal PIλDμ controller design for induction motor speed control system. Int. J. Electr. Eng. Inform. 2019, 11, 638–661. [Google Scholar] [CrossRef]
- Colin-Cervantes, J.D.; Sanchez-Lopez, C.; Ochoa-Montiel, R.; Torres-Muñoz, D.; Hernandez-Mejia, C.M.; Sanchez-Gaspariano, L.A.; Gonzalez-Hernandez, H.G. Rational approximations of arbitrary order: A survey. Fractal Fract. 2021, 5, 267. [Google Scholar] [CrossRef]
- Reddy, A.S.; Reddy, G.N. Novel applications of Oustaloup recursive approximation and modified Oustaloup recursive approximation methods in linear fractional order control design. Int. J. Dyn. Control 2024, 12, 2236–2246. [Google Scholar] [CrossRef]
- Yuan, I.; Xiu, G.; Shi, B. Equivalence of the Initialized Riemann-Liouville Derivatives and the Initialized Caputo Derivatives. arXiv 2018, arXiv:1811.11537. [Google Scholar]
- Merrikh-Bayat, F.; Karimi-Ghartemani, M. Some properties of three-term fractional order system. Fract. Calc. Appl. Anal. (FCAA) 2008, 11, 3. Available online: http://www.diogenes.bg/fcaa/volume11/fcaa113/FMBayat_MK%20Ghartemani_fcaa113.pdf (accessed on 1 November 2024).
- Wang, F.Y. The exact and unique solution for phase-lead and phase-lag compensation. IEEE Trans. Educ. 2003, 46, 258–262. [Google Scholar] [CrossRef]
- Muñiz-Montero, C.; Sánchez-Gaspariano, L.A.; Sánchez-López, C.; González-Díaz, V.R.; Tlelo-Cuautle, E. On the electronic realizations of fractional-order phase-lead-lag compensators with opamps and FPAAs. In Fractional Order Control and Synchronization of Chaotic Systems; Azar, A., Vaidyanathan, S., Ouannas, A., Eds.; Studies in Computational Intelligence; Springer: Cham, Switzerland, 2017; Volume 688, pp. 95–118. [Google Scholar] [CrossRef]
- Kumarasamy, V.; Thottam, K.; Ramasamy, V.; Chrasekaran, G.; Chinnaraj, G.; Sivalingam, P.; Kumar, N.S. A review of integer order PID and fractional order PID controllers using optimization techniques for speed control of brushless DC motor drive. Int. J. Syst. Assur. Eng. Manag. 2023, 14, 1139–1150. [Google Scholar] [CrossRef]
- Da Silva, C.S.; Da Silva, N.J.; Júnior, F.A.; Medeiros, R.L.; Silva, L.E.; Lucena, V.F. Experimental implementation of hydraulic turbine dynamics and a fractional order speed governor controller on a small-scale power system. IEEE Access 2024, 12, 40480–40495. [Google Scholar] [CrossRef]
- Rahimian, M.A.; Tavazoei, M.S. Improving integral square error performance with implementable fractional-order PI controllers. Optim. Control. Appl. Methods 2014, 35, 303–323. [Google Scholar] [CrossRef]
- Roongmuanpha, N.; Satansup, J.; Pukkalanun, T.; Tangsrirat, W. Design of mixed-mode analog PID controller with CFOAs. Sensors 2024, 24, 3125. [Google Scholar] [CrossRef]
- Adhikari, A.; Schaffer, J. Modified Lilliefors test. J. Mod. Appl. Stat. Methods 2015, 14, 53–69. [Google Scholar] [CrossRef]
- Schultz, B.B. Levene’s test for relative variation. Syst. Biol. 1985, 34, 449–456. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Angel, L.; Viola, J. Design and statistical robustness analysis of FOPID, IOPID and SIMC PID controllers applied to a motor-generator system. IEEE Lat. Am. Trans. 2015, 13, 3724–3734. [Google Scholar] [CrossRef]
- Makhbouche, A.; Boudjehem, B.; Birs, I.; Muresan, C.I. Fractional-order PID controller based on immune feedback mechanism for time-delay systems. Fractal Fract. 2023, 7, 53. [Google Scholar] [CrossRef]
- Skogestad, S. Simple analytic rules for model reduction and PID controller tuning. J. Process. Control 2003, 13, 291–309. [Google Scholar] [CrossRef]
- Li, Y.; Ang, K.H.; Chong, G.C.Y. PID control system analysis and design. IEEE Control Syst. Mag. 2006, 26, 32–41. [Google Scholar] [CrossRef]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. FOMCON: A MATLAB toolbox for fractional-order system identification and control. Int. J. Microelectron. Comput. Sci. 2011, 2, 51–62. [Google Scholar]
- Duddeti, B.B.; Naskar, A.K.; Meena, V.; Bahadur, J.; Meena, P.K.; Hameed, I.A. FOMCON toolbox-based direct approximation of fractional order systems using gaze cues learning-based grey wolf optimizer. Fractal Fract. 2024, 8, 477. [Google Scholar] [CrossRef]
- Muñiz-Montero, C.; Munoz-Pacheco, J.M.; Arizaga-Silva, J.A.; Martínez, W.O. Exploring Four Direct Synthesis Scenarios for Fractional-Order Controllers. Authorea 2024. [Google Scholar] [CrossRef]




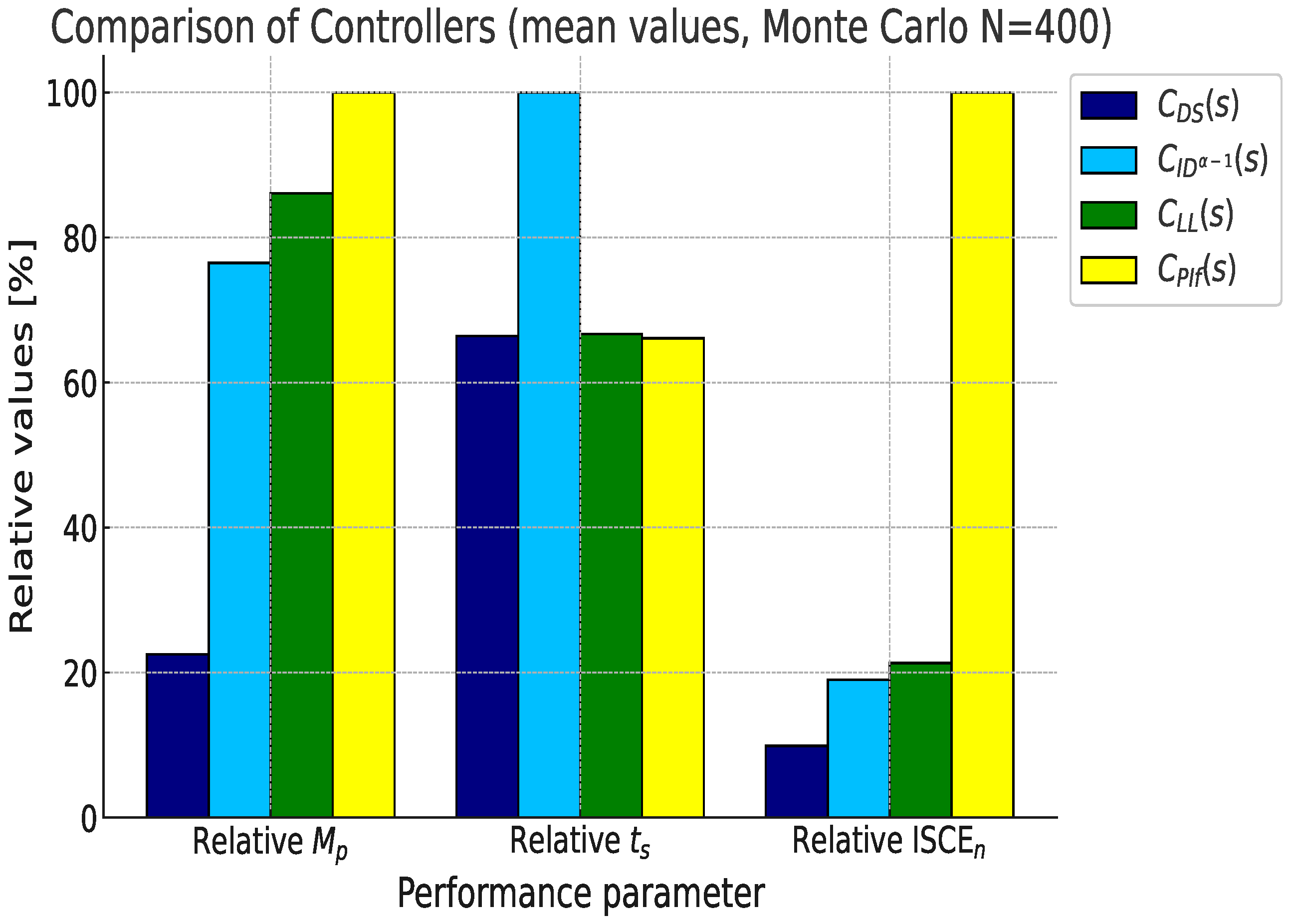

| 64.63∘ | 64.63∘ | 64.63∘ | 60∘ | |
| 5% | 5% | 5% | 8.7% | |
| 0.0693 | 0.01 | 0.003 | 0.01 | |
| 1000 s | 586 s | 2000 s | 586 s | |
| A | −40 dB | - | - | −40 dB |
| 0.6% | 3.7% | 4% | 5.5% | |
| 858 s | 1838 s | 1104 s | 997 s | |
| 0.1 | 0.1 | 0.1 | 0.1 | |
| 3.2 | 4.5 | 6.8 | 12.4 | |
| 857 s | 832 s | 650 s | 640 s | |
| 5.94 | 18 | 1.78 | 31.17 |
| Param | ||
| M = 1.4%, SD = 1.9% | M = 4.8%, SD = 3.8% | |
| M = 1116.4 s, SD = 330.2 s | M = 1660.9 s, SD = 299.2 s | |
| M = 0.1, SD = 0.02 | M = 0.1, SD = 0.03 | |
| M = 3.9, SD = 2.2 | M = 7.6, SD = 2.8 | |
| Param | ||
| M = 5.4%, SD = 5.7% | M = 6.3%, SD = 6.5% | |
| M = 1224 s, SD = 361.9 s | M = 1113.4 s, SD = 244.7 s | |
| M = 0.1, SD = 0.02 | M = 0.1, SD = 0.02 | |
| M = 8.6, SD = 5.9 | M = 40.8, SD = 2.6 |
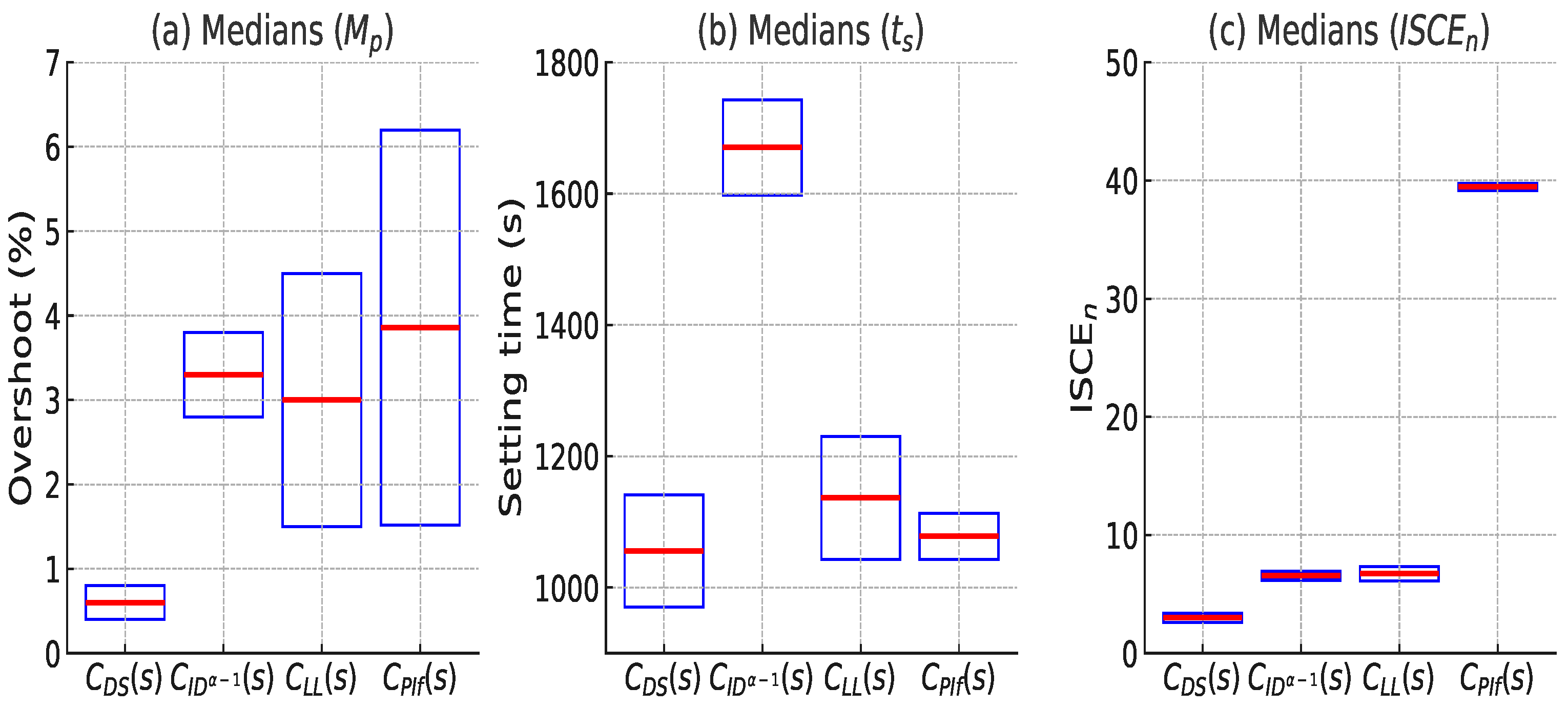
| Parameter | ||||
|---|---|---|---|---|
| Median | 0.49 | 3.18 | 2.80 | 3.02 |
| C. Interval | (0.41, 0.68) | (2.67, 3.55) | (0.79, 4.11) | (1.05, 4.74) |
| Median (s) | 1043.8 | 1684.8 | 1134.5 | 1066.2 |
| C. Interval (s) | (971.2, 1116.4) | (1546.9, 1761.2) | (1071.0, 1204.6) | (1014.7, 1083.7) |
| Median | 3.21 | 4.61 | 6.91 | 39.28 |
| C. Interval | (3.01, 3.36) | (4.39, 4.83) | (6.27, 7.41) | (39.06, 39.56) |
| Method | Analytical | Analytical | Analytical | Numerical |
| (2 equations) | -Numerical | (4 equations | (FOMCON) | |
| Bode plots) | ||||
| No. of parameters | 4 | 3 | 3 | 5 |
| Parameters | , , A, | , , | , , | , , A, , |
| Difficulty | Easy | Medium | Medium | Medium |
| Position in | ||||
| the comparison | ||||
| 1st | 4th | 2nd | 3rd | |
| 1st | 4th | 3rd | 2nd | |
| Energy efficiency | 1st | 2nd | 3rd | 4th |
| No. of parameters | 2nd | 3rd | 3rd | 1st |
| adjusted |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñiz-Montero, C.; Munoz-Pacheco, J.M.; Sánchez-Gaspariano, L.A.; Sánchez-López, C.; Molinar-Solís, J.E.; Chavez-Portillo, M. Direct Synthesis of Fractional-Order Controllers Using Only Two Design Equations with Robustness to Parametric Uncertainties. Fractal Fract. 2025, 9, 101. https://doi.org/10.3390/fractalfract9020101
Muñiz-Montero C, Munoz-Pacheco JM, Sánchez-Gaspariano LA, Sánchez-López C, Molinar-Solís JE, Chavez-Portillo M. Direct Synthesis of Fractional-Order Controllers Using Only Two Design Equations with Robustness to Parametric Uncertainties. Fractal and Fractional. 2025; 9(2):101. https://doi.org/10.3390/fractalfract9020101
Chicago/Turabian StyleMuñiz-Montero, Carlos, Jesus M. Munoz-Pacheco, Luis A. Sánchez-Gaspariano, Carlos Sánchez-López, Jesús E. Molinar-Solís, and Melissa Chavez-Portillo. 2025. "Direct Synthesis of Fractional-Order Controllers Using Only Two Design Equations with Robustness to Parametric Uncertainties" Fractal and Fractional 9, no. 2: 101. https://doi.org/10.3390/fractalfract9020101
APA StyleMuñiz-Montero, C., Munoz-Pacheco, J. M., Sánchez-Gaspariano, L. A., Sánchez-López, C., Molinar-Solís, J. E., & Chavez-Portillo, M. (2025). Direct Synthesis of Fractional-Order Controllers Using Only Two Design Equations with Robustness to Parametric Uncertainties. Fractal and Fractional, 9(2), 101. https://doi.org/10.3390/fractalfract9020101










