Hybrid Fourier Series and Weighted Residual Function Method for Caputo-Type Fractional PDEs with Variable Coefficients
Abstract
1. Introduction
- Time-fractional sub-diffusion models, as explored in [7,8,9,10,11], constitute a prominent subclass of fractional PDEs that describe anomalous transport phenomena in which the mean squared displacement grows sub-linearly with time. These models typically involve Caputo derivatives of order , which capture memory effects and non-local temporal behavior. They are particularly effective in modeling processes such as contaminant diffusion in porous media, charge transport in disordered systems, and biological diffusion involving trapping mechanisms.
- Time-fractional telegraph equations, as discussed in [12,13], extend classical telegraph models by incorporating fractional-order time derivatives, typically of the Caputo type. These equations are particularly effective in capturing the wave–diffusion duality in media exhibiting memory effects, such as viscoelastic materials or biological tissues. The fractional order enables the modeling of damped wave propagation with non-local temporal behavior, providing a more accurate representation of signal transmission, relaxation phenomena, and anomalous transport processes.
- Multi-term time-fractional diffusion and diffusion-wave models, as introduced in [14,15,16,17], extend classical formulations by incorporating multiple fractional derivatives of distinct orders. These models are particularly effective in capturing complex memory effects and layered temporal dynamics, which are often observed in heterogeneous media and viscoelastic systems. By accommodating a combination of sub-diffusive and wave-like behaviors, multi-term formulations provide enhanced flexibility for simulating anomalous transport, relaxation phenomena, and hybrid diffusion–wave processes.
- Anomalous sub-diffusion equations involving fractional-time operators, as presented in [18,19,20,21,22,23,24,25], are formulated to model transport processes in which particle motion deviates from classical Brownian behavior. These equations typically involve Caputo derivatives of order , effectively capturing long-range temporal correlations and memory effects. Such models are especially relevant in heterogeneous or disordered media, where trapping, crowding, or structural complexity gives rise to sub-linear scaling of the mean squared displacement. Owing to their flexibility and accuracy, these models serve as valuable tools in fields from geophysics and biology to materials science and finance.
2. Basic Definitions and Notations
3. Solution Framework and Implementation
3.1. Decomposition of the Main Equation
3.2. Solution of the Obtained Independent Time-Fractional ODEs (10)
3.3. Convergence Analysis
- The integral exists and is finite;
- possesses a finite number of local extrema over its domain;
- contains a finite number of finite discontinuities.
3.4. Computational Procedure Corresponding to the Introduced Method
| Algorithm 1: Hybrid Fourier Series and Weighted Residual Function Method for Solving FPDE (1) |
Input: , . ; ; if then ; end if fordo end for ; ; ifthen ; end if ifthen ; else ifthen ; for do ; ; end for end if ; ; Construct: ; fordo ; ; ; ; if then ; ; else ifthen ; ; end if ; ; Construct: ; ; ; Construct: ; end for . |
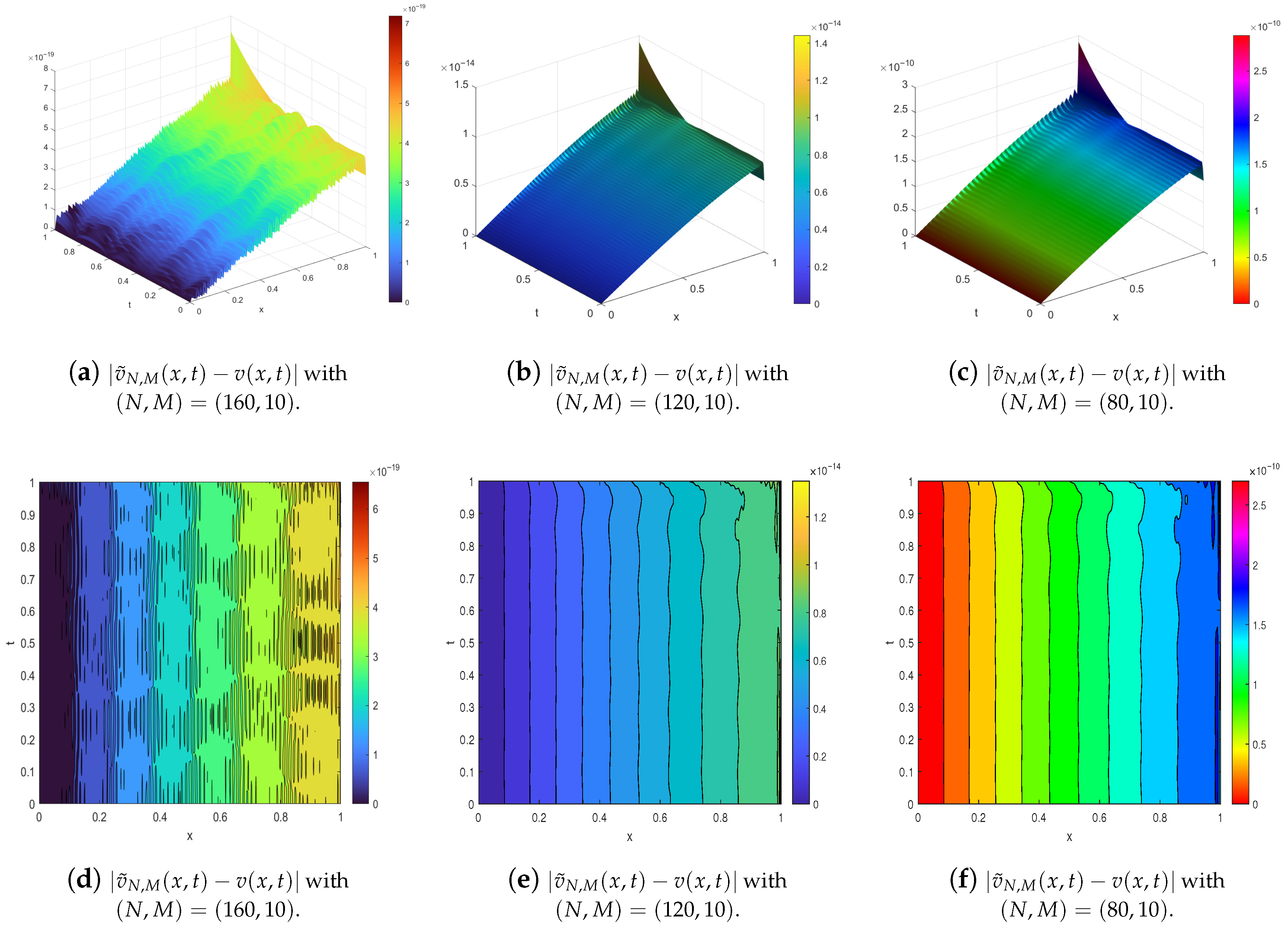
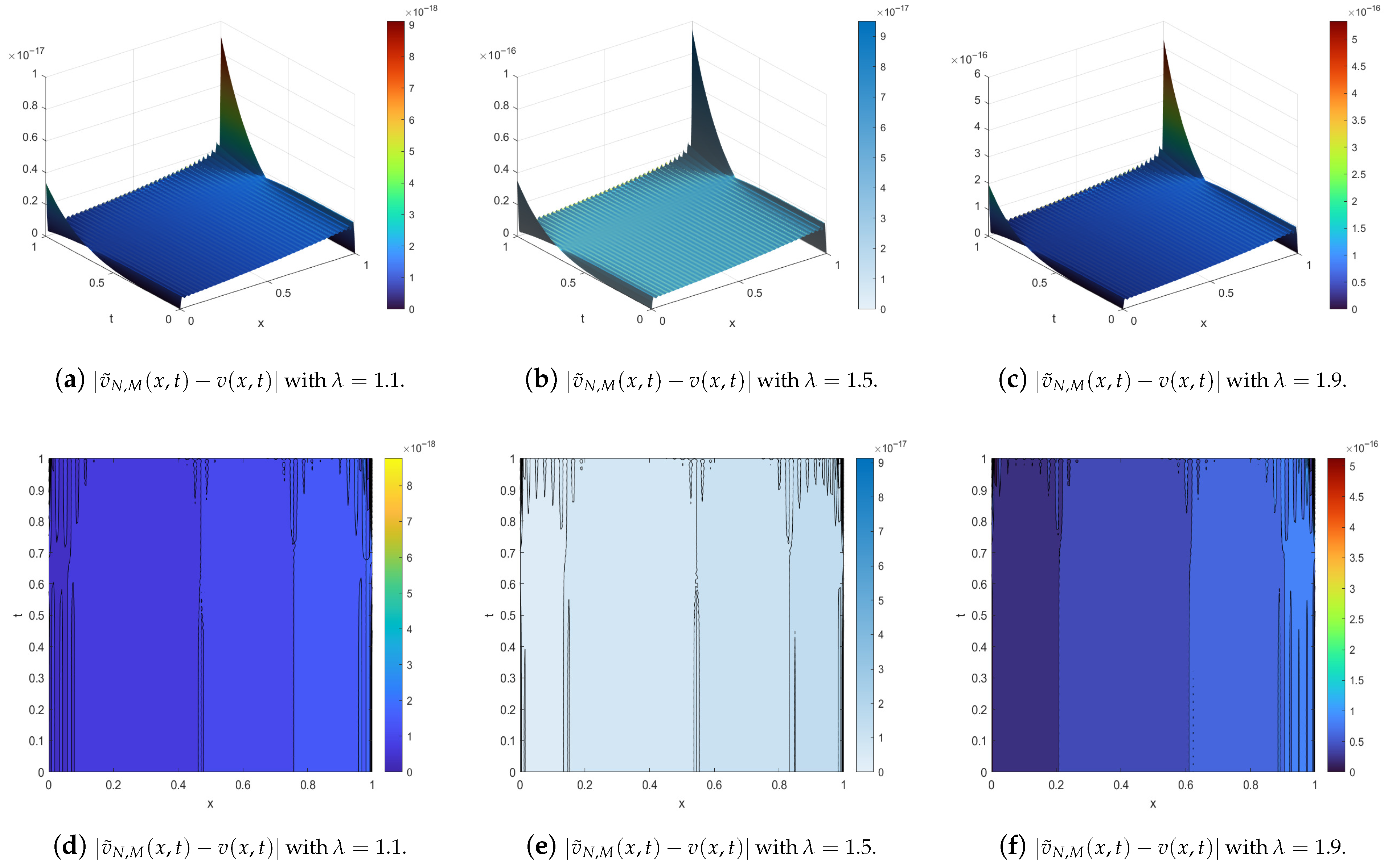
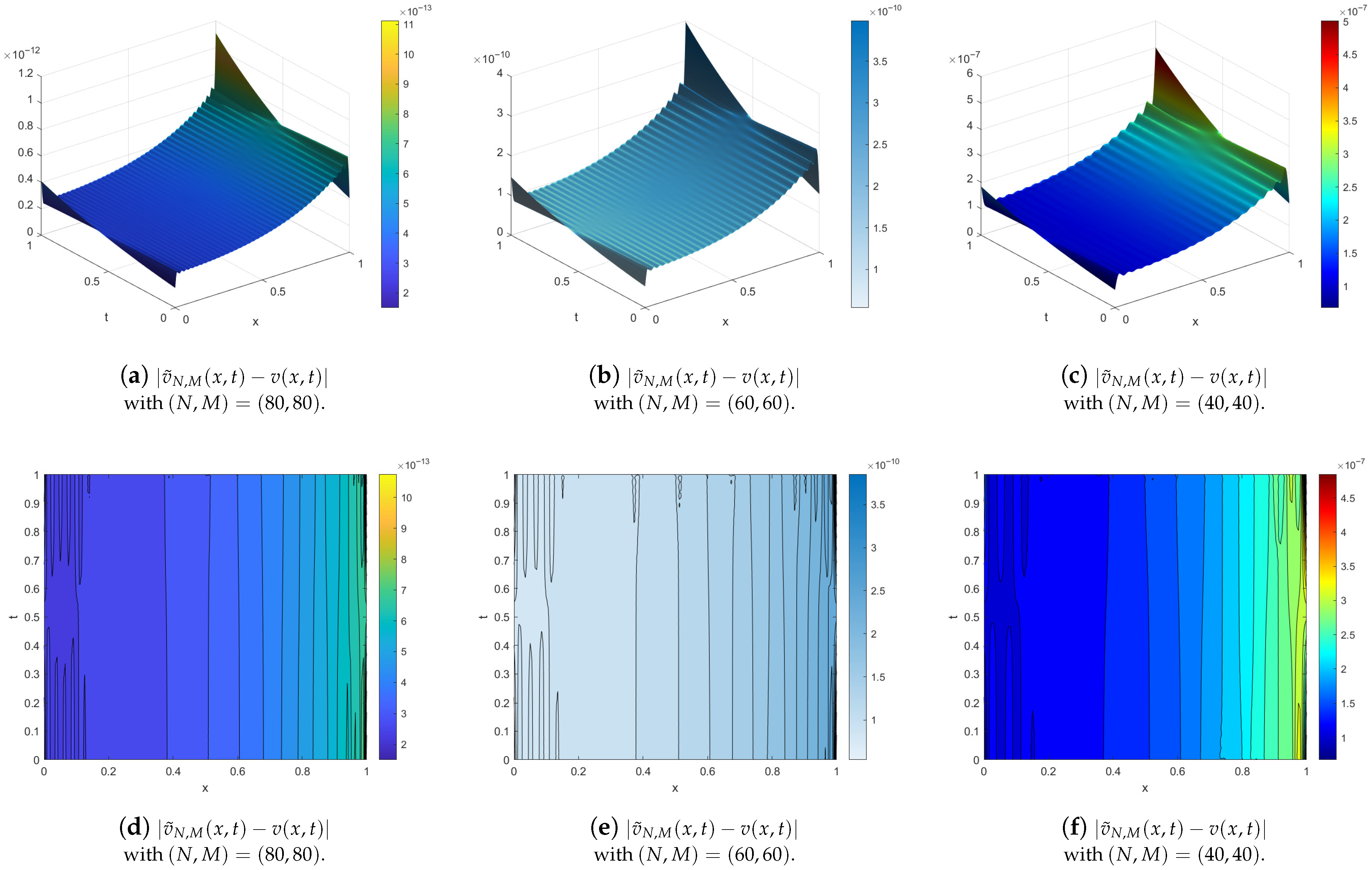
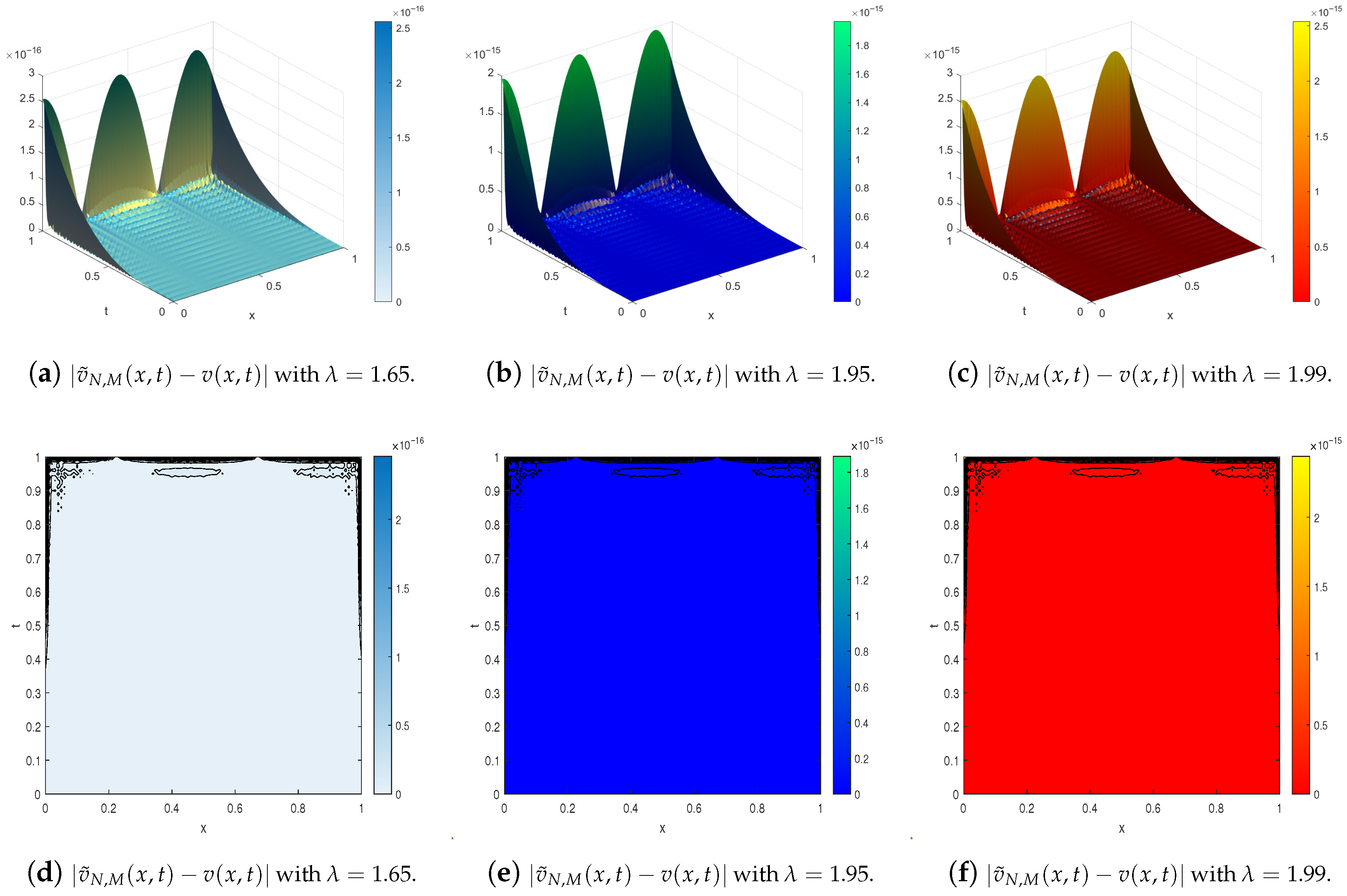
4. Illustrative Examples
- The exact solution is used as a reference;
- The numerical solution is computed using the developed method;
- Error metrics, including absolute error, relative error, and root mean square error (RMSE), are evaluated to quantify accuracy;
- Computational efficiency is discussed, including convergence behavior and sensitivity to parameters such as , M, and N.
- Has high accuracy across a range of test cases.
- Exhibits robustness with respect to variations in fractional order and discretization parameters.
- Maintains stability and convergence even for stiff or singular problems.
- Max absolute error (M.A.E.):
- Relative error (R.E.):
- Root mean square of errors (R.M.S.E.):
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Number of FLOPs
Appendix A.1. Computational Procedure Corresponding to the Proposed Method
Appendix A.2. Computational Cost of Constructing the Residual Functions
Appendix A.3. Formation and Solution of the Linear Systems
Appendix A.4. Computational Cost of Constructing the Approximate Solution
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar] [CrossRef]
- Das, S. Functional Fractional Calculus for System Identification and Controls; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010; Volume 2004. [Google Scholar] [CrossRef]
- Cui, Z.; Yu, P.; Mao, Z. Existence of solutions for nonlocal boundary value problems of nonlinear fractional differential equations. Adv. Dyn. Syst. Appl. 2012, 7, 31–40. [Google Scholar]
- Hashemi, M. Invariant subspaces admitted by fractional differential equations with conformable derivatives. Chaos Solitons Fractals 2018, 107, 161–169. [Google Scholar] [CrossRef]
- Gao, G.H.; Sun, Z.Z.; Zhang, H.W. A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 2014, 259, 33–50. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, C. Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 2007, 225, 1533–1552. [Google Scholar] [CrossRef]
- Cui, M. Compact finite difference method for the fractional diffusion equation. J. Comput. Phys. 2009, 228, 7792–7804. [Google Scholar] [CrossRef]
- Khader, M. On the numerical solutions for the fractional diffusion equation. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2535–2542. [Google Scholar] [CrossRef]
- Zeng, F.; Li, C.; Liu, F.; Turner, I. Numerical algorithms for time-fractional subdiffusion equation with second-order accuracy. SIAM J. Sci. Comput. 2015, 37, A55–A78. [Google Scholar] [CrossRef]
- Bahşı, A.K.; Yalçınbaş, S. Numerical solutions and error estimations for the space fractional diffusion equation with variable coefficients via Fibonacci collocation method. SpringerPlus 2016, 5, 1375. [Google Scholar] [CrossRef]
- Mollahasani, N.; Moghadam, M.M.M.; Afrooz, K. A new treatment based on hybrid functions to the solution of telegraph equations of fractional order. Appl. Math. Model. 2016, 40, 2804–2814. [Google Scholar] [CrossRef]
- Xu, X.; Xu, D. Legendre wavelets direct method for the numerical solution of time-fractional order telegraph equations. Mediterr. J. Math. 2018, 15, 1–33. [Google Scholar] [CrossRef]
- Dehghan, M.; Safarpoor, M.; Abbaszadeh, M. Two high-order numerical algorithms for solving the multi-term time fractional diffusion-wave equations. J. Comput. Appl. Math. 2015, 290, 174–195. [Google Scholar] [CrossRef]
- Bhrawy, A.; Doha, E.; Baleanu, D.; Ezz-Eldien, S. A spectral tau algorithm based on Jacobi operational matrix for numerical solution of time fractional diffusion-wave equations. J. Comput. Phys. 2015, 293, 142–156. [Google Scholar] [CrossRef]
- Zheng, M.; Liu, F.; Anh, V.; Turner, I. A high-order spectral method for the multi-term time-fractional diffusion equations. Appl. Math. Model. 2016, 40, 4970–4985. [Google Scholar] [CrossRef]
- Dehghan, M.; Abbaszadeh, M.; Deng, W. Fourth-order numerical method for the space–time tempered fractional diffusion-wave equation. Appl. Math. Lett. 2017, 73, 120–127. [Google Scholar] [CrossRef]
- Liu, F.; Yang, C.; Burrage, K. Numerical method and analytical technique of the modified anomalous subdiffusion equation with a nonlinear source term. J. Comput. Appl. Math. 2009, 231, 160–176. [Google Scholar] [CrossRef]
- Mohebbi, A.; Abbaszadeh, M.; Dehghan, M. A high-order and unconditionally stable scheme for the modified anomalous fractional sub-diffusion equation with a nonlinear source term. J. Comput. Phys. 2013, 240, 36–48. [Google Scholar] [CrossRef]
- Wang, Z.; Vong, S. Compact difference schemes for the modified anomalous fractional sub-diffusion equation and the fractional diffusion-wave equation. J. Comput. Phys. 2014, 277, 1–15. [Google Scholar] [CrossRef]
- Dehghan, M.; Abbaszadeh, M.; Mohebbi, A. Legendre spectral element method for solving time fractional modified anomalous sub-diffusion equation. Appl. Math. Model. 2016, 40, 3635–3654. [Google Scholar] [CrossRef]
- Cao, X.; Cao, X.; Wen, L. The implicit midpoint method for the modified anomalous sub-diffusion equation with a nonlinear source term. J. Comput. Appl. Math. 2017, 318, 199–210. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M.; Zhou, Y. Alternating direction implicit-spectral element method (ADI-SEM) for solving multi-dimensional generalized modified anomalous sub-diffusion equation. Comput. Math. Appl. 2019, 78, 1772–1792. [Google Scholar] [CrossRef]
- Kheybari, S.; Darvishi, M.T.; Hashemi, M.S. A semi-analytical approach to Caputo type time-fractional modified anomalous sub-diffusion equations. Appl. Numer. Math. 2020, 158, 103–122. [Google Scholar] [CrossRef]
- Kheybari, S.; Alizadeh, F.; Darvishi, M.T.; Hosseini, K. A Fourier Series Technique for Approximate Solutions of Modified Anomalous Time-Fractional Sub-Diffusion Equations. Fractal Fract. 2024, 8, 718. [Google Scholar] [CrossRef]
- Li, X.; Xu, C. Existence and uniqueness of the weak solution of the space-time fractional diffusion equation and a spectral method approximation. Commun. Comput. Phys. 2010, 8, 1016. [Google Scholar] [CrossRef]
- Chen, J.; Liu, F.; Anh, V. Analytical solution for the time-fractional telegraph equation by the method of separating variables. J. Math. Anal. Appl. 2008, 338, 1364–1377. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, F.; Turner, I.; Burrage, K. Analytical solutions for the multi-term time–space Caputo–Riesz fractional advection–diffusion equations on a finite domain. J. Math. Anal. Appl. 2012, 389, 1117–1127. [Google Scholar] [CrossRef]
- Zaky, M.A. Existence, uniqueness and numerical analysis of solutions of tempered fractional boundary value problems. Appl. Numer. Math. 2019, 145, 429–457. [Google Scholar] [CrossRef]
- Stojanović, M.; Gorenflo, R. Nonlinear two-term time fractional diffusion-wave problem. Nonlinear Anal. Real World Appl. 2010, 11, 3512–3523. [Google Scholar] [CrossRef]
- Alizadeh, F.; Hashemi, M.S.; Haji-Badali, A. Lie symmetries, exact solutions, and conservation laws of the nonlinear time-fractional Benjamin-Ono equation. Comput. Methods Differ. Equ. 2022, 10, 608–616. [Google Scholar] [CrossRef]
- Alizadeh, F.; Hincal, E.; Hosseini, K.; Hashemi, M.S.; Das, A. The (2 + 1)-dimensional generalized time-fractional Zakharov Kuznetsov Benjamin Bona Mahony equation: Its classical and nonclassical symmetries, exact solutions, and conservation laws. Opt. Quantum Electron. 2023, 55, 1061. [Google Scholar] [CrossRef]
- Reutskiy, S.; Lin, J. A semi-analytic collocation method for space fractional parabolic PDE. Int. J. Comput. Math. 2018, 95, 1326–1339. [Google Scholar] [CrossRef]
- Reutskiy, S. A new semi-analytical collocation method for solving multi-term fractional partial differential equations with time variable coefficients. Appl. Math. Model. 2017, 45, 238–254. [Google Scholar] [CrossRef]
- Aylin Bayrak, M.; Demir, A. A new approach for space-time fractional partial differential equations by residual power series method. Appl. Math. Comput. 2018, 336, 215–230. [Google Scholar] [CrossRef]
- Kheybari, S. Numerical algorithm to Caputo type time–space fractional partial differential equations with variable coefficients. Math. Comput. Simul. 2021, 182, 66–85. [Google Scholar] [CrossRef]
- Kheybari, S.; Alizadeh, F.; Darvishi, M.T.; Hosseini, K.; Hincal, E. A Novel Semi-Analytical Scheme to Deal with Fractional Partial Differential Equations (PDEs) of Variable-Order. Fractal Fract. 2024, 8, 425. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Dehghan, M. A new operational matrix for solving fractional-order differential equations. Comput. Math. Appl. 2010, 59, 1326–1336. [Google Scholar] [CrossRef]
- Dehghan, M.; Manafian, J.; Saadatmandi, A. Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Methods Partial. Differ. Equ. Int. J. 2010, 26, 448–479. [Google Scholar] [CrossRef]
- Kheybari, S.; Darvishi, M. An efficient technique to find semi-analytical solutions for higher order multi-point boundary value problems. Appl. Math. Comput. 2018, 336, 76–93. [Google Scholar] [CrossRef]
- Kheybari, S.; Darvishi, M.T.; Alizadeh, F.; Hincal, E.; Hosseini, K.; Chen, X. Solving Multi-Point Boundary Value Differential Equations with a Novel Semi-Analytical Algorithm. Int. J. Comput. Methods 2025, 22, 2450086. [Google Scholar] [CrossRef]
- Borwein, P.; Erdélyi, T.; Zhang, J. Müntz systems and orthogonal Müntz-Legendre polynomials. Trans. Am. Math. Soc. 1994, 342, 523–542. [Google Scholar] [CrossRef] [PubMed]
- Mokhtary, P.; Ghoreishi, F.; Srivastava, H. The Müntz-Legendre Tau method for fractional differential equations. Appl. Math. Model. 2016, 40, 671–684. [Google Scholar] [CrossRef]
- Jeffrey, A. Advanced Engineering Mathematics; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Mulimani, M.; Kumbinarasaiah, S. Numerical solution of time-fractional telegraph equations using wavelet transform. Int. J. Dyn. Control 2024, 12, 2166–2189. [Google Scholar] [CrossRef]
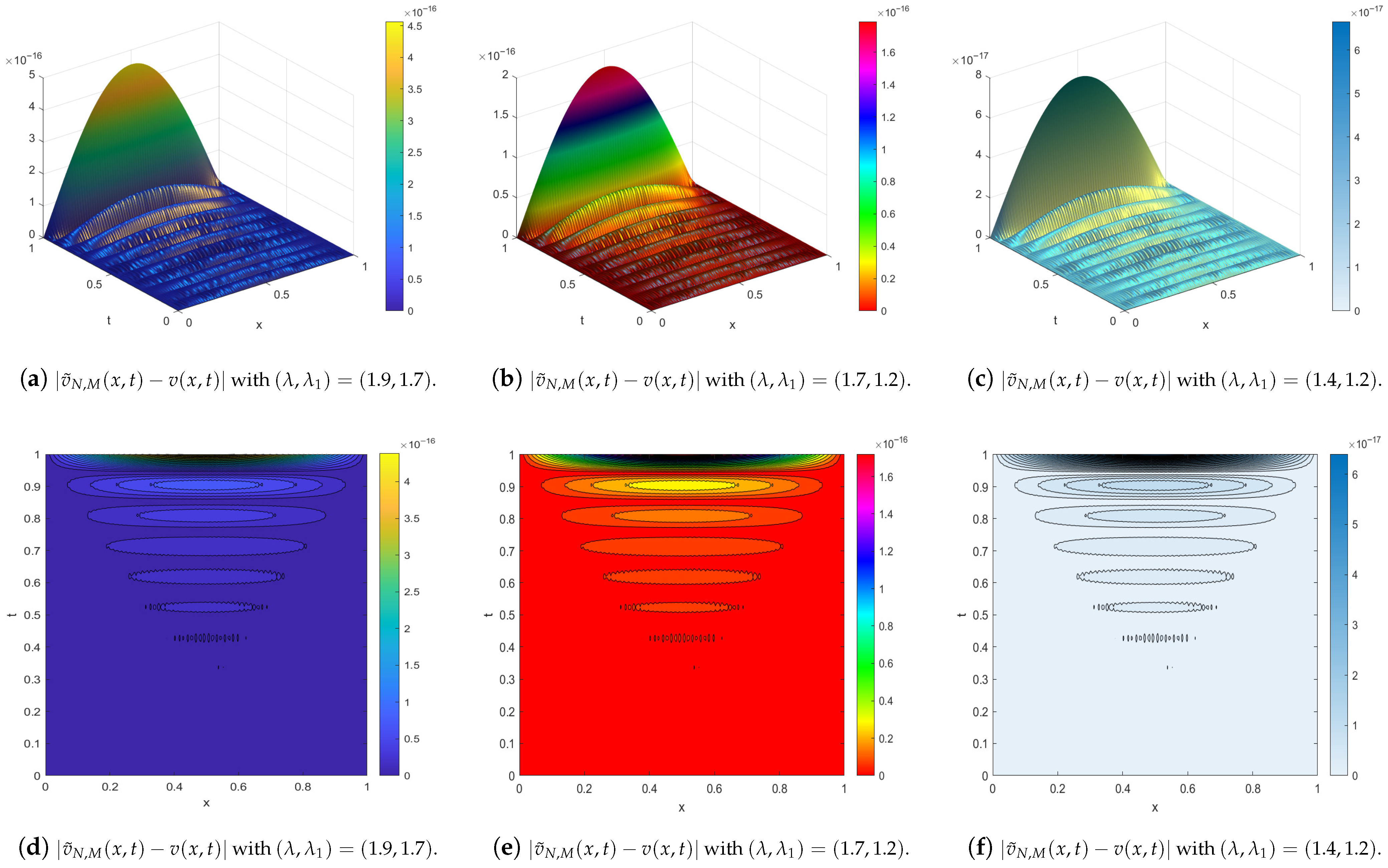
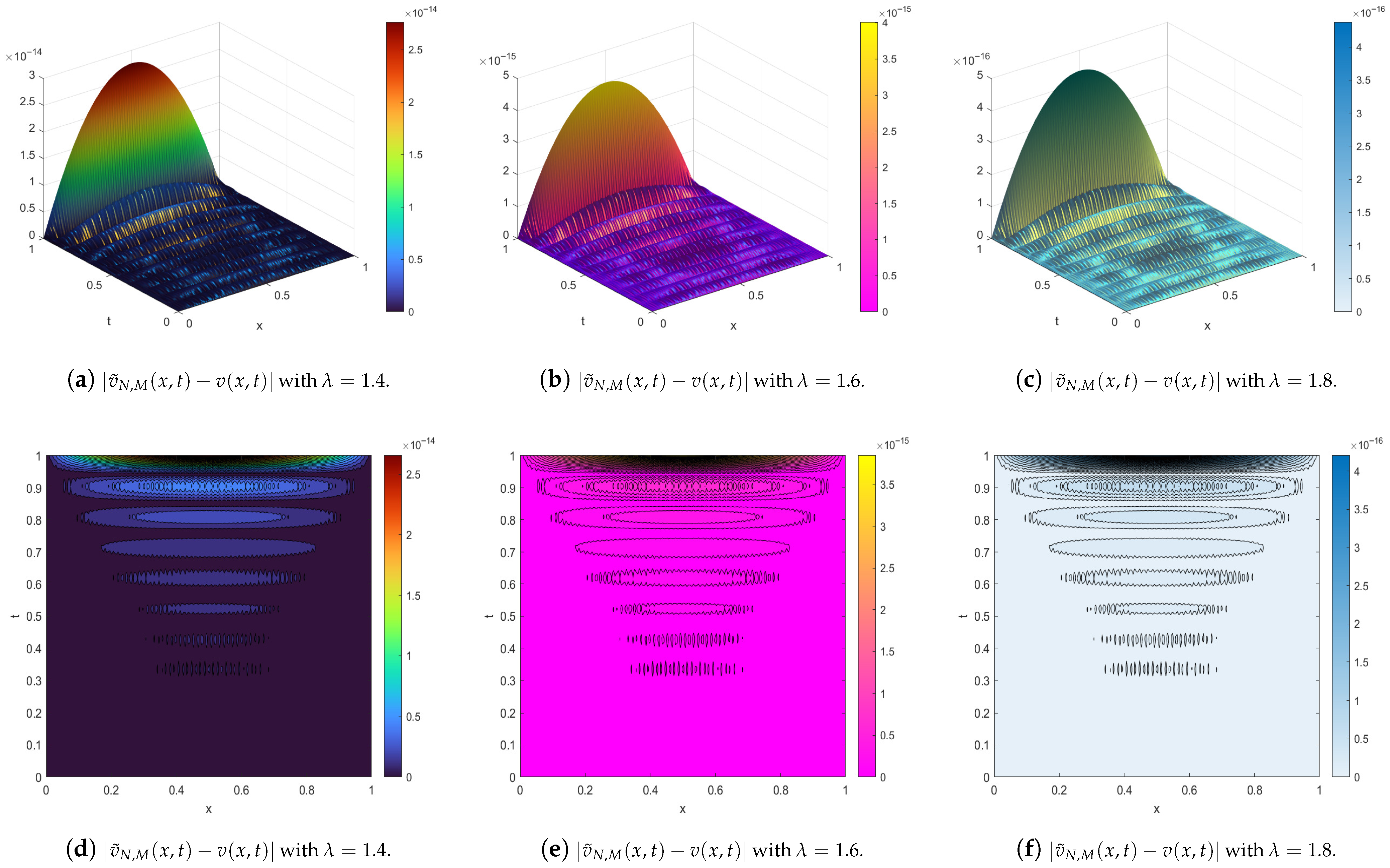
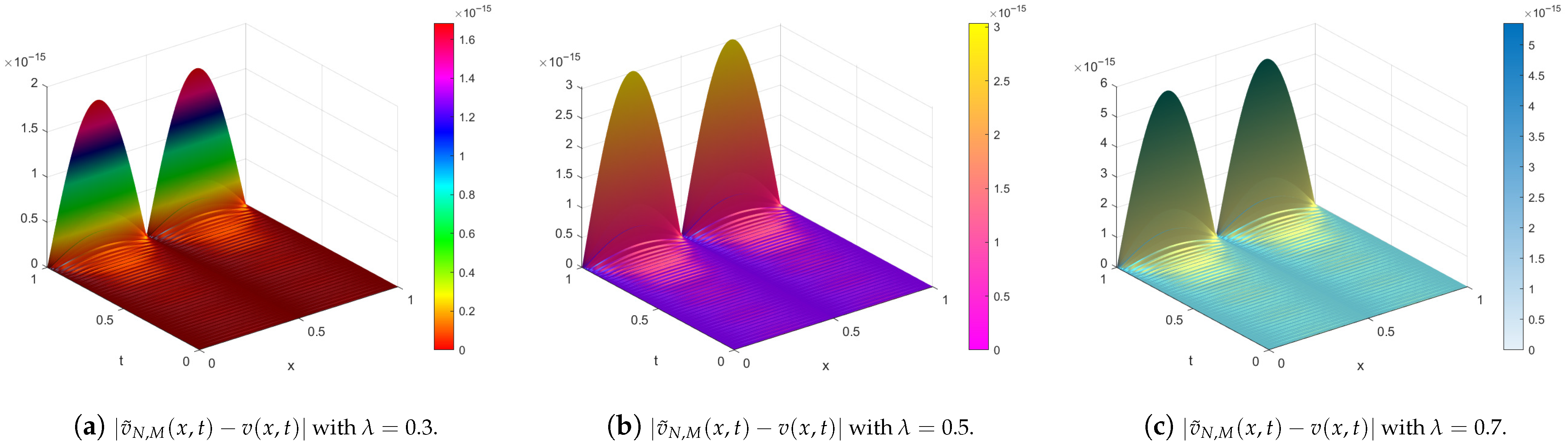
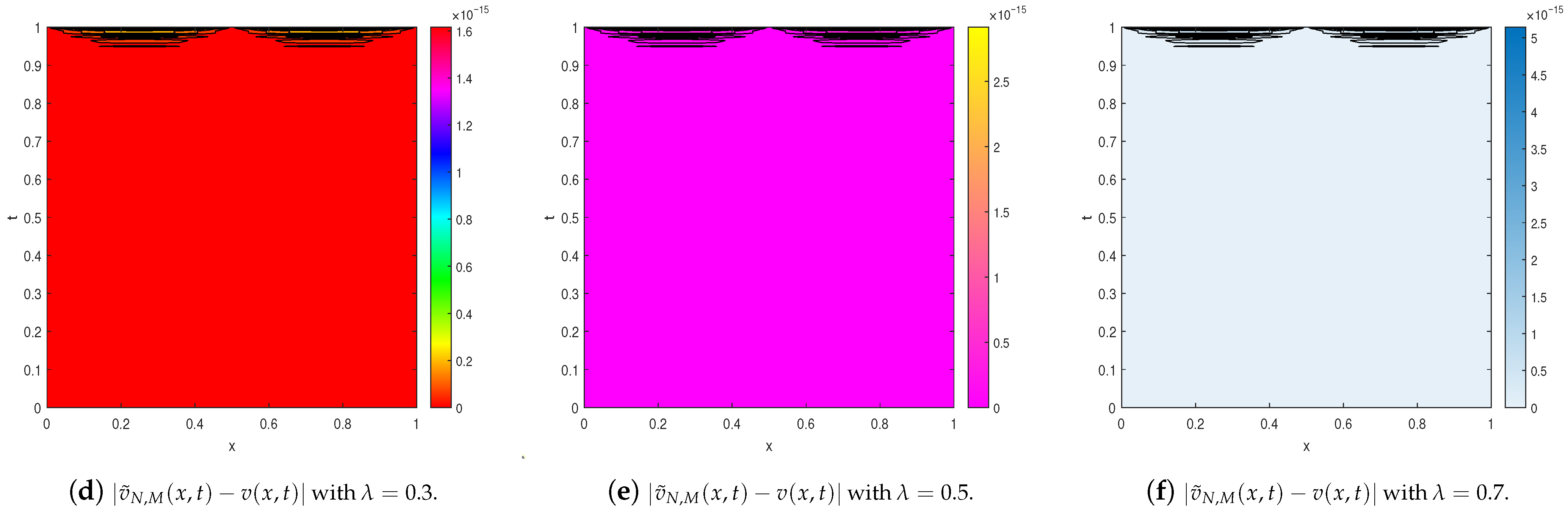
| Our Results | Method [14] | ||||||
|---|---|---|---|---|---|---|---|
| 10 | 10 | ||||||
| 20 | |||||||
| 40 | |||||||
| 80 | |||||||
| 160 | |||||||
| 10 | 10 | ||||||
| 20 | |||||||
| 40 | |||||||
| 80 | |||||||
| 160 | |||||||
| 10 | 10 | ||||||
| 20 | |||||||
| 40 | |||||||
| 80 | |||||||
| 160 | |||||||
| N | M | M.A.E. | R.E. | R.M.S.E. | CPU Time (s) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1.9 | 1.3 | 20 | 10 | |||||||
| 40 | ||||||||||
| 60 | ||||||||||
| 80 | ||||||||||
| 100 | ||||||||||
| 120 | ||||||||||
| 140 | ||||||||||
| 160 | ||||||||||
| 1.7 | 1.2 | 20 | 10 | |||||||
| 40 | ||||||||||
| 60 | ||||||||||
| 80 | ||||||||||
| 100 | ||||||||||
| 120 | ||||||||||
| 140 | ||||||||||
| 160 | ||||||||||
| 1.4 | 1.2 | 20 | 10 | |||||||
| 40 | ||||||||||
| 60 | ||||||||||
| 80 | ||||||||||
| 100 | ||||||||||
| 120 | ||||||||||
| 140 | ||||||||||
| 160 | ||||||||||
| Our Results | Method [15] | ||||||
|---|---|---|---|---|---|---|---|
| 60 | 10 | 0 | 0 | 1 | |||
| 70 | 1 | 1 | |||||
| 80 | |||||||
| 90 | |||||||
| 100 | |||||||
| 60 | 10 | 0 | 0 | 1 | |||
| 70 | 1 | 1 | |||||
| 80 | |||||||
| 90 | |||||||
| 100 | |||||||
| 60 | 10 | 0 | 0 | 1 | |||
| 70 | 1 | 1 | |||||
| 80 | |||||||
| 90 | |||||||
| 100 | |||||||
| N | M | M.A.E. | R.E. | R.M.S.E. | CPU Time (s) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1.4 | 20 | 10 | |||||||
| 40 | |||||||||
| 60 | |||||||||
| 80 | |||||||||
| 100 | |||||||||
| 120 | |||||||||
| 140 | |||||||||
| 160 | |||||||||
| 1.6 | 20 | 10 | |||||||
| 40 | |||||||||
| 60 | |||||||||
| 80 | |||||||||
| 100 | |||||||||
| 120 | |||||||||
| 140 | |||||||||
| 160 | |||||||||
| 1.8 | 20 | 10 | |||||||
| 40 | |||||||||
| 60 | |||||||||
| 80 | |||||||||
| 100 | |||||||||
| 120 | |||||||||
| 140 | |||||||||
| 160 | |||||||||
| Our Results | Method [20] | |||||
|---|---|---|---|---|---|---|
| 10 | 10 | |||||
| 20 | 20 | |||||
| 30 | 30 | |||||
| 40 | 40 | |||||
| 50 | 50 | |||||
| 60 | 60 | |||||
| 10 | 10 | |||||
| 20 | 20 | |||||
| 30 | 30 | |||||
| 40 | 40 | |||||
| 50 | 50 | |||||
| 60 | 60 | |||||
| 10 | 10 | |||||
| 20 | 20 | |||||
| 30 | 30 | |||||
| 40 | 40 | |||||
| 50 | 50 | |||||
| 60 | 60 | |||||
| N | M | M.A.E. | R.E. | R.M.S.E. | CPU Time (s) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0.3 | 10 | 10 | |||||||
| 20 | 20 | ||||||||
| 30 | 30 | ||||||||
| 40 | 40 | ||||||||
| 50 | 50 | ||||||||
| 60 | 60 | ||||||||
| 70 | 70 | ||||||||
| 80 | 80 | ||||||||
| 0.5 | 10 | 10 | |||||||
| 20 | 20 | ||||||||
| 30 | 30 | ||||||||
| 40 | 40 | ||||||||
| 50 | 50 | ||||||||
| 60 | 60 | ||||||||
| 70 | 70 | ||||||||
| 80 | 80 | ||||||||
| 0.7 | 10 | 10 | |||||||
| 20 | 20 | ||||||||
| 30 | 30 | ||||||||
| 40 | 40 | ||||||||
| 50 | 50 | ||||||||
| 60 | 60 | ||||||||
| 70 | 70 | ||||||||
| 80 | 80 | ||||||||
| Our Results | Method [36] | ||||
|---|---|---|---|---|---|
| 40 | 10 | 16 | 4 | ||
| 60 | 8 | ||||
| 80 | 12 | ||||
| 100 | 16 | ||||
| 120 | 20 | ||||
| 140 | 24 | ||||
| 160 | 28 | ||||
| N | M | M.A.E. | R.E. | R.M.S.E. | CPU Time (s) | |||
|---|---|---|---|---|---|---|---|---|
| 20 | 10 | |||||||
| 40 | ||||||||
| 60 | ||||||||
| 80 | ||||||||
| 100 | ||||||||
| 120 | ||||||||
| 140 | ||||||||
| 160 | ||||||||
| Our Results | Method [13] | |||||
|---|---|---|---|---|---|---|
| 10 | 10 | 2 | 3 | |||
| 20 | 20 | 4 | ||||
| 30 | 30 | 5 | ||||
| 40 | 40 | 6 | ||||
| 50 | 50 | 7 | ||||
| 60 | 60 | 8 | ||||
| 10 | 10 | 2 | 3 | |||
| 20 | 20 | 4 | ||||
| 30 | 30 | 5 | ||||
| 40 | 40 | 6 | ||||
| 50 | 50 | 7 | ||||
| 60 | 60 | 8 | ||||
| 10 | 10 | 2 | 3 | |||
| 20 | 20 | 4 | ||||
| 30 | 30 | 5 | ||||
| 40 | 40 | 6 | ||||
| 50 | 50 | 7 | ||||
| 60 | 60 | 8 | ||||
| N | M | M.A.E. | R.E. | R.M.S.E. | CPU Time (s) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1.1 | 10 | 10 | |||||||
| 20 | 20 | ||||||||
| 30 | 30 | ||||||||
| 40 | 40 | ||||||||
| 50 | 50 | ||||||||
| 60 | 60 | ||||||||
| 70 | 70 | ||||||||
| 80 | 80 | ||||||||
| 1.5 | 10 | 10 | |||||||
| 20 | 20 | ||||||||
| 30 | 30 | ||||||||
| 40 | 40 | ||||||||
| 50 | 50 | ||||||||
| 60 | 60 | ||||||||
| 70 | 70 | ||||||||
| 80 | 80 | ||||||||
| 1.9 | 10 | 10 | |||||||
| 20 | 20 | ||||||||
| 30 | 30 | ||||||||
| 40 | 40 | ||||||||
| 50 | 50 | ||||||||
| 60 | 60 | ||||||||
| 70 | 70 | ||||||||
| 80 | 80 | ||||||||
| Absolute Errors of Our Obtained Results for | Reported Results in [13] for | |||||
|---|---|---|---|---|---|---|
| N | M | M.A.E. | R.E. | R.M.S.E. | CPU Time (s) | |||
|---|---|---|---|---|---|---|---|---|
| 10 | 10 | |||||||
| 20 | 20 | |||||||
| 30 | 30 | |||||||
| 40 | 40 | |||||||
| 50 | 50 | |||||||
| 60 | 60 | |||||||
| 70 | 70 | |||||||
| 80 | 80 | |||||||
| Absolute Errors of Our Obtained Results for | Reported Results in [13] for | Reported Results in [45] for | ||||
|---|---|---|---|---|---|---|
| 1.25 | ||||||
| 1.65 | ||||||
| 1.95 | ||||||
| 1.99 | ||||||
| N | M | M.A.E. | R.E. | R.M.S.E. | CPU Time (s) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1.25 | 10 | 10 | |||||||
| 20 | 20 | ||||||||
| 30 | 30 | ||||||||
| 40 | 40 | ||||||||
| 50 | 50 | ||||||||
| 60 | 60 | ||||||||
| 70 | 70 | ||||||||
| 80 | 80 | ||||||||
| 1.65 | 10 | 10 | |||||||
| 20 | 20 | ||||||||
| 30 | 30 | ||||||||
| 40 | 40 | ||||||||
| 50 | 50 | ||||||||
| 60 | 60 | ||||||||
| 70 | 70 | ||||||||
| 80 | 80 | ||||||||
| 1.95 | 10 | 10 | |||||||
| 20 | 20 | ||||||||
| 30 | 30 | ||||||||
| 40 | 40 | ||||||||
| 50 | 50 | ||||||||
| 60 | 60 | ||||||||
| 70 | 70 | ||||||||
| 80 | 80 | ||||||||
| 1.99 | 10 | 10 | |||||||
| 20 | 20 | ||||||||
| 30 | 30 | ||||||||
| 40 | 40 | ||||||||
| 50 | 50 | ||||||||
| 60 | 60 | ||||||||
| 70 | 70 | ||||||||
| 80 | 80 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kheybari, S.; Alizadeh, F.; Darvishi, M.T.; Hosseini, K. Hybrid Fourier Series and Weighted Residual Function Method for Caputo-Type Fractional PDEs with Variable Coefficients. Fractal Fract. 2025, 9, 765. https://doi.org/10.3390/fractalfract9120765
Kheybari S, Alizadeh F, Darvishi MT, Hosseini K. Hybrid Fourier Series and Weighted Residual Function Method for Caputo-Type Fractional PDEs with Variable Coefficients. Fractal and Fractional. 2025; 9(12):765. https://doi.org/10.3390/fractalfract9120765
Chicago/Turabian StyleKheybari, Samad, Farzaneh Alizadeh, Mohammad Taghi Darvishi, and Kamyar Hosseini. 2025. "Hybrid Fourier Series and Weighted Residual Function Method for Caputo-Type Fractional PDEs with Variable Coefficients" Fractal and Fractional 9, no. 12: 765. https://doi.org/10.3390/fractalfract9120765
APA StyleKheybari, S., Alizadeh, F., Darvishi, M. T., & Hosseini, K. (2025). Hybrid Fourier Series and Weighted Residual Function Method for Caputo-Type Fractional PDEs with Variable Coefficients. Fractal and Fractional, 9(12), 765. https://doi.org/10.3390/fractalfract9120765








