Advances in the Application of Fractal Theory to Oil and Gas Resource Assessment
Abstract
1. Introduction
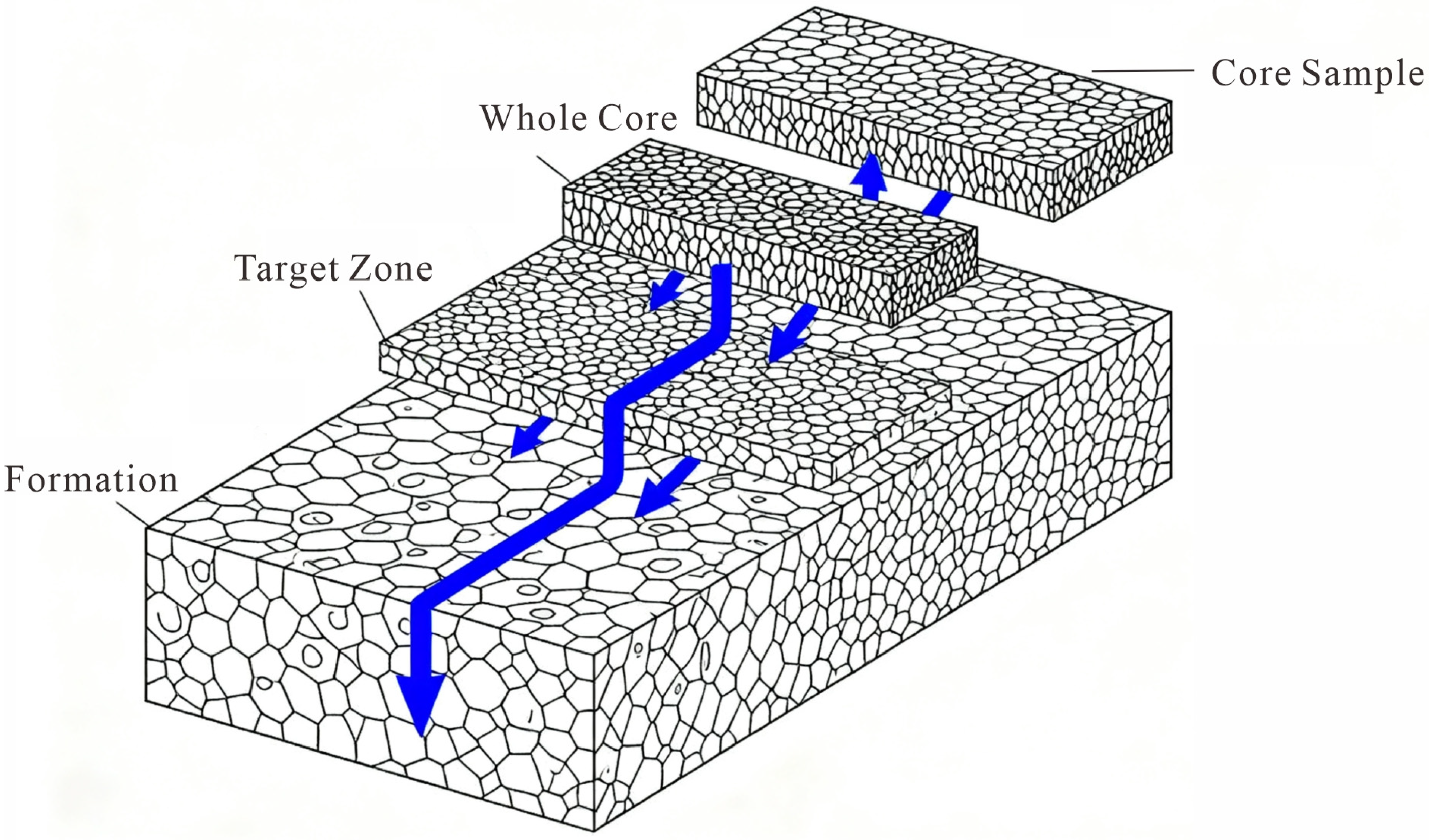
2. Methodology
3. Overview of Fractal Theory
4. Fractal Theory and Hydrocarbon Resource Assessment
4.1. Historical Development
4.2. Application Context
5. Application of Fractal Theory in Hydrocarbon Resource Assessment
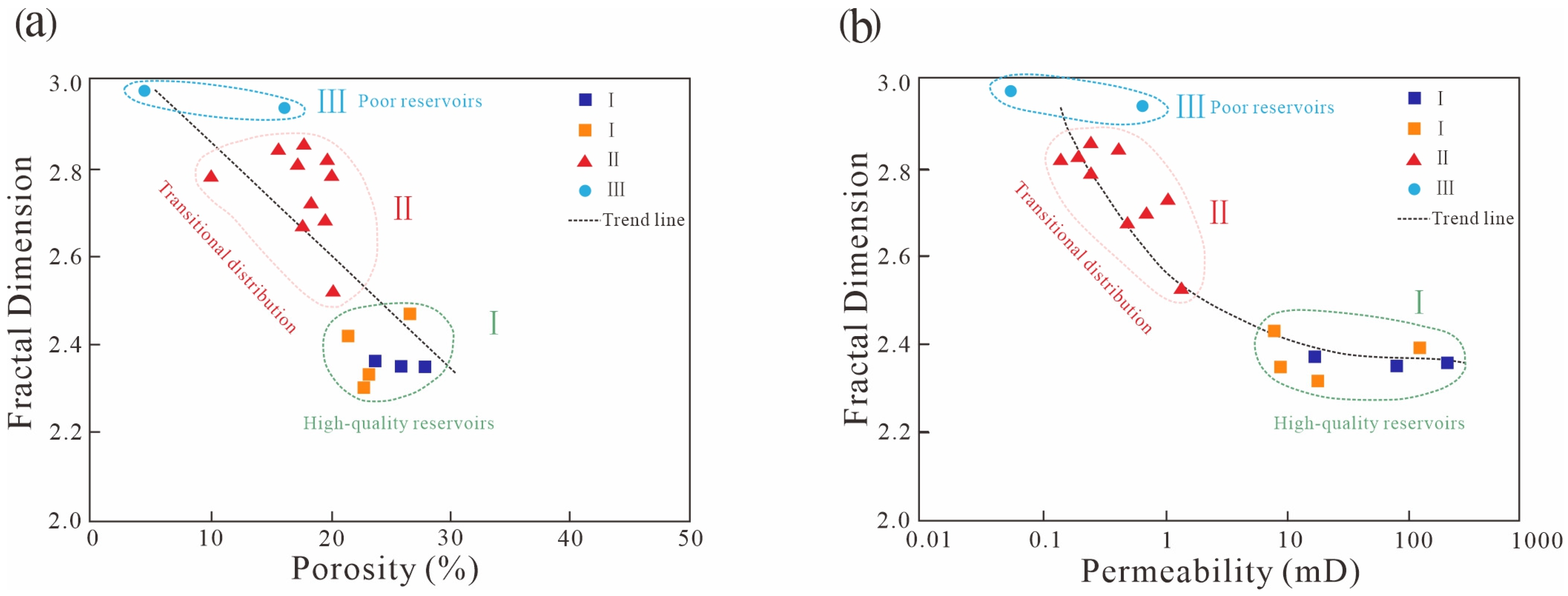
5.1. Reservoir Classification and Evaluation
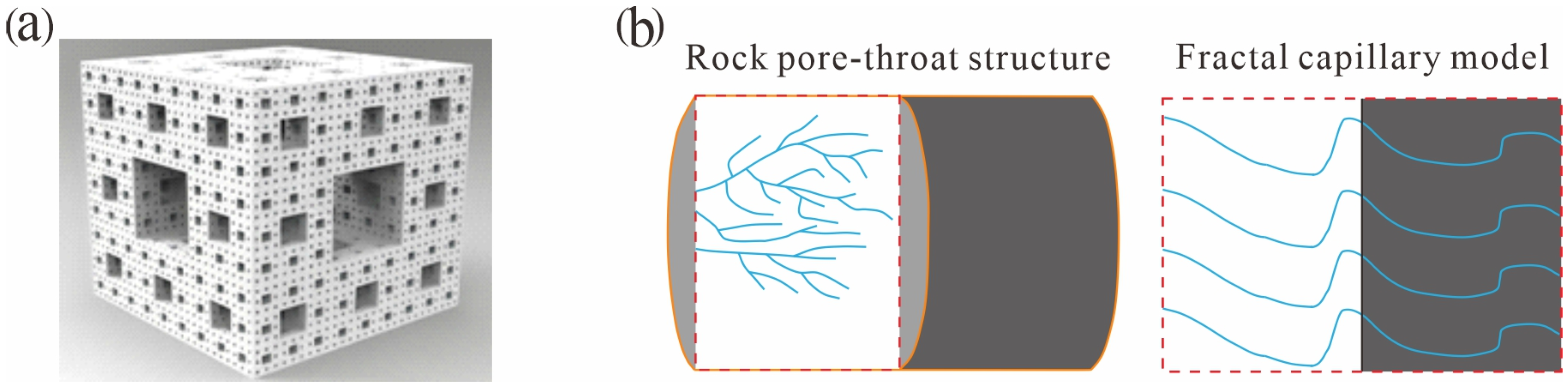
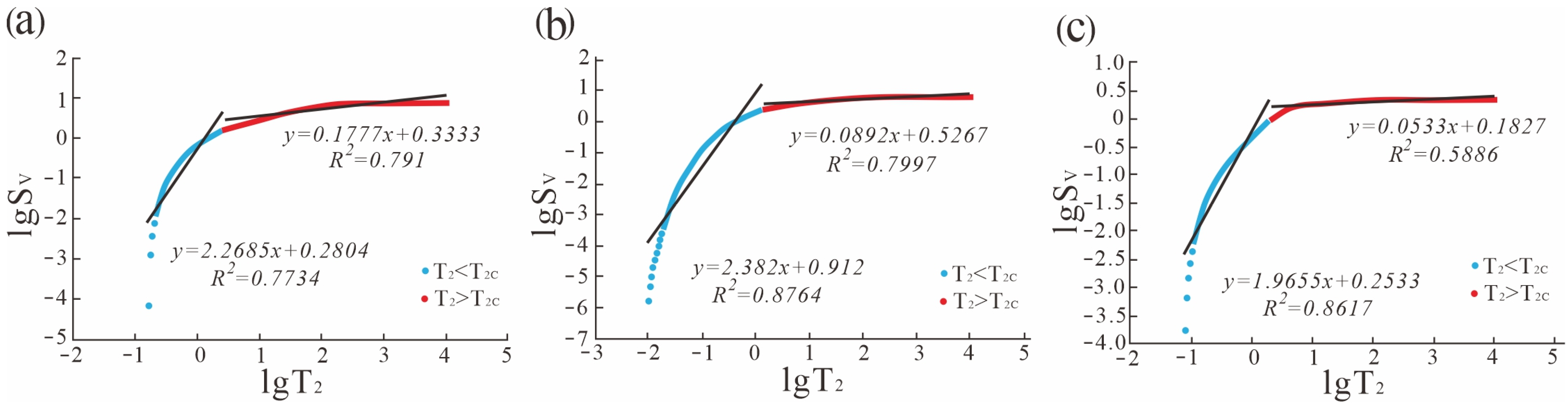
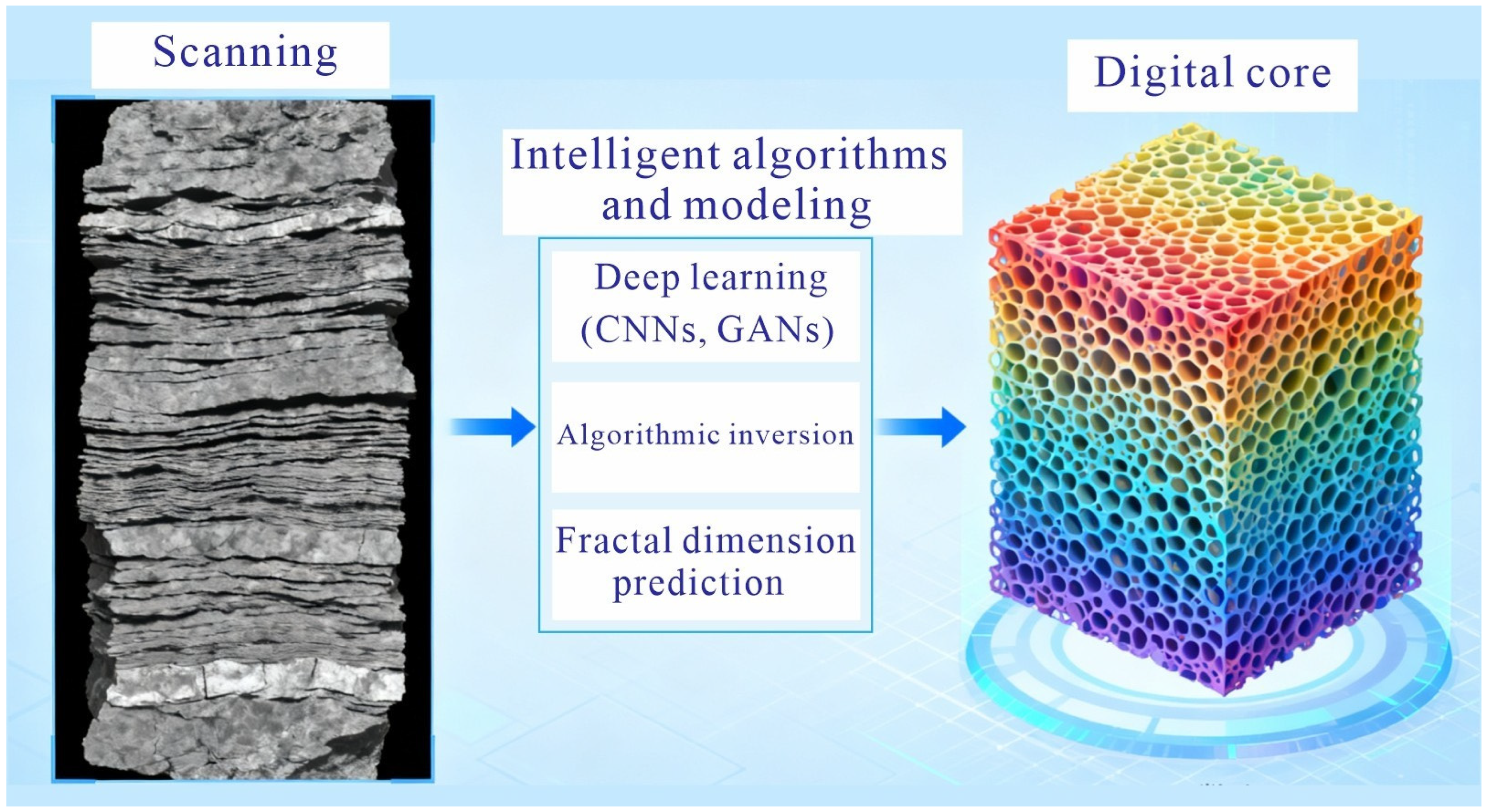
5.2. Fractal Characterization of Reservoir Pore Structures
5.3. Fractal Theory and Applications in Flow Behavior Characterization
5.4. Fractal Modeling and Evaluation of Fracture Systems
6. Development Trends
7. Discussion
7.1. Advantages of Fractal Theory in Petroleum Applications
7.2. Limitations and Challenges of Fractal Theory in Petroleum Applications
7.3. Controversial Studies and Divergent Interpretations
7.4. Discussion on Method Universality and Research Sufficiency
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two dimensional |
| 3D | Three dimensional |
| BET | Brunauer–Emmett–Teller |
| CO2 | Carbon dioxide |
| CRMI | Constant-rate mercury injection |
| CT | Computed tomography |
| D | Fractal dimension |
| DFN | Discrete fracture network |
| FHH | Frenkel–Halsey–Hill |
| GRNN | Generalized Regression Neural Network |
| HPMI | High-pressure mercury injection |
| MICP | Mercury injection capillary pressure |
| NMR | Nuclear magnetic resonance |
| SEM | Scanning electron microscopy |
| SRV | Stimulated Reservoir Volume |
| UAV | Unmanned Aerial Vehicle |
| XRD | X-ray diffraction |
References
- Litvinenko, V. The role of hydrocarbons in the global energy agenda: The focus on liquefied natural gas. Resources 2020, 9, 59. [Google Scholar] [CrossRef]
- Egorov, A.S.; Prischepa, O.M.; Nefedov, Y.V.; Kontorovich, V.A.; Vinokurov, L.Y. Deep structure, tectonics and petroleum potential of the western sector of the Russian arctic. J. Mar. Sci. Eng. 2021, 9, 258. [Google Scholar] [CrossRef]
- Jin, Z. Hydrocarbon accumulation and resources evaluation: Recent advances and current challenges. Adv. Geo-Energy Res. 2023, 8, 1–4. [Google Scholar] [CrossRef]
- Mi, S.; Guo, Q.; Zhang, Q.; Wang, J. Classification and potential of continental shale oil resources in China and resource evaluation methods and criteria. Oil Shale 2023, 40, 283–320. [Google Scholar] [CrossRef]
- Wang, Y.; Li, N.; Pang, X.; Zhang, H.; Wang, C.; Yao, Y. Evolutionary mechanisms of pore-fracture network development in oil shale during pyrolysis: Current research progress and perspectives. Sustain. Energy Fuels 2025, 9, 3495–3522. [Google Scholar] [CrossRef]
- Wang, Y.; Zhong, B.; Yang, L.; Zhu, Y.; Xiang, J.; Zhang, T.; Zhang, H. Multiscale Fractal Evolution Mechanism of Pore Heterogeneity in Hydrocarbon Source Rocks: A Thermal Simulation Experiment in the Xiamaling Formation. Fractal Fract. 2025, 9, 351. [Google Scholar] [CrossRef]
- Rahner, M.S.; Halisch, M.; Fernandes, C.P.; Weller, A.; dos Santos, V.S.S. Fractal dimensions of pore spaces in unconventional reservoir rocks using X-ray nano-and micro-computed tomography. J. Nat. Gas Sci. Eng. 2018, 55, 298–311. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, N.; Fadlelmula, M.; Wang, Y. Structural regeneration of fracture-vug network in naturally fractured vuggy reservoirs. J. Pet. Sci. Eng. 2018, 165, 28–41. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals and the rebirth of iteration theory. In The Beauty of Fractals: Images of Complex Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1986; pp. 151–160. [Google Scholar] [CrossRef]
- Giles, J. Benoit Mandelbrot: Father of fractals. Nature 2004, 432, 266–268. [Google Scholar] [CrossRef]
- Dong, S.; Yu, X.; Zeng, L.; Ye, J.; Wang, L.; Ji, C.; Fu, K.; Wang, R. Relationship between box-counting fractal dimension and properties of fracture networks. Unconv. Resour. 2024, 4, 100068. [Google Scholar] [CrossRef]
- Li, B.; Zhang, T.; Bai, L.; Miao, X. Estimation of Undiscovered Hydrocarbon Resources Potential through Fractal Geometry Based on GIS. In Proceedings of the 2009 International Workshop on Chaos-Fractals Theories and Applications, Shenyang, China, 6–8 November 2009; pp. 399–403. [Google Scholar] [CrossRef]
- Guo, Q.; Ren, H.; Wu, X.; Liu, Z.; Wei, Y.; Liu, J.; Liu, H.; Yu, J.; Zhang, Q. A fractal simulation method for simulating the resource abundance of oil and gas and its application. Math. Geosci. 2022, 54, 873–901. [Google Scholar] [CrossRef]
- Ji, G.; Li, K.; Zhang, G.; Li, S.; Zhang, L. An assessment method for shale fracability based on fractal theory and fracture toughness. Eng. Fract. Mech. 2019, 211, 282–290. [Google Scholar] [CrossRef]
- Liu, B.; Yao, L.; Fu, X.; He, B.; Bai, L. Application of the fractal method to the characterization of organic heterogeneities in shales and exploration evaluation of shale oil. J. Mar. Sci. Eng. 2019, 7, 88. [Google Scholar] [CrossRef]
- Barton, C.C.; Scholz, C.H. The fractal size and spatial distribution of hydrocarbon accumulations: Implications for resource assessment and exploration strategy. In Fractals in Petroleum Geology and Earth Processes; Springer: Boston, MA, USA, 1995; pp. 13–34. [Google Scholar] [CrossRef]
- Hu, B.; Wang, J.G.; Sun, R.; Zhao, Z. A permeability model for the fractal tree-like fracture network with self-affine surface roughness in shale gas reservoirs. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 24. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, S.; Yang, Y.; Zhang, P.; Wei, G. Numerical simulation by hydraulic fracturing engineering based on fractal theory of fracture extending in the coal seam. J. Nat. Gas Geosci. 2016, 1, 319–325. [Google Scholar] [CrossRef]
- Habib, M.; Yao, G.; Xie, C.; Charles, S.P.; Jakada, H.; Danlami, M.S.; Ahmed, H.A.; Omeiza, I.A. Optimizing oil and gas field management through a fractal reservoir study model. J. Pet. Explor. Prod. Technol. 2017, 7, 43–53. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G. Fractal analysis of tight gas sandstones using high-pressure mercury intrusion techniques. J. Nat. Gas Sci. Eng. 2015, 24, 185–196. [Google Scholar] [CrossRef]
- He, T.; Zhou, Y.; Chen, Z.; Zhang, Z.; Xie, H.; Shang, Y.; Cui, G. Fractal characterization of the pore-throat structure in tight sandstone based on low-temperature nitrogen gas adsorption and high-pressure mercury injection. Fractal Fract. 2024, 8, 356. [Google Scholar] [CrossRef]
- Turlapati, V.Y.; Prusty, B.K.; Bakshi, T. Detailed pore structure study of Damodar Valley and upper Assam basin shales using fractal analysis. Energy Fuels 2020, 34, 14001–14011. [Google Scholar] [CrossRef]
- Liu, F.; Yang, M.; Wu, K.; Zong, J.; Song, H.; Wang, F. Pore structure characterization and permeability prediction with fractal theory considering the tortuosity effect. Fuel 2025, 394, 134978. [Google Scholar] [CrossRef]
- You, X.T.; Liu, J.Y.; Jia, C.S.; Li, J.; Liao, X.Y.; Zheng, A.W. Production data analysis of shale gas using fractal model and fuzzy theory: Evaluating fracturing heterogeneity. Appl. Energy 2019, 250, 1246–1259. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Li, T.; Liang, Z.; Meng, S.; Zheng, L.; Wu, N. Fracture Complexity and Mineral Damage in Shale Hydraulic Fracturing Based on Microscale Fractal Analysis. Fractal Fract. 2025, 9, 535. [Google Scholar] [CrossRef]
- Palmore, J. A review of nonlinear dynamics, chaos and fractals. J. Geol. Educ. 1991, 39, 393–397. [Google Scholar] [CrossRef]
- Aguirre, J.; Viana, R.L.; Sanjuán, M.A. Fractal structures in nonlinear dynamics. Rev. Mod. Phys. 2009, 81, 333–386. [Google Scholar] [CrossRef]
- Guo, H.; Yuan, L.; Cheng, Y.; Wang, K.; Xu, C. Experimental investigation on coal pore and fracture characteristics based on fractal theory. Powder Technol. 2019, 346, 341–349. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, C.; Ning, L.; Zhao, H.; Bi, J. Pore and fracture development in coal under stress conditions based on nuclear magnetic resonance and fractal theory. Fuel 2022, 309, 122112. [Google Scholar] [CrossRef]
- Cai, J.; You, Q. Fractal theory and its application in studying the feature of landforms. In Proceedings of the 2010 International Workshop on Chaos-Fractal Theories and Applications, Kunming, China, 29–31 October 2010; pp. 440–444. [Google Scholar] [CrossRef]
- Gallos, L.K.; Song, C.; Makse, H.A.A. review of fractality and self-similarity in complex networks. Phys. A Stat. Mech. Its Appl. 2007, 386, 686–691. [Google Scholar] [CrossRef]
- Lapidus, M.L.; Radunović, G. An Invitation to Fractal Geometry: Fractal Dimensions, Self-Similarity, and Fractal Curves; American Mathematical Society: Providence, RI, USA, 2024; Volume 247. [Google Scholar]
- Velde, B.; Dubois, J.; Moore, D.; Touchard, G. Fractal patterns of fractures in granites. Earth Planet. Sci. Lett. 1991, 104, 25–35. [Google Scholar] [CrossRef]
- Higuchi, T. Relationship between the fractal dimension and the power law index for a time series: A numerical investigation. Phys. D Nonlinear Phenom. 1990, 46, 254–264. [Google Scholar] [CrossRef]
- Zhang, B.; Yu, B.; Wang, H.; Yun, M. A fractal analysis of permeability for power-law fluids in porous media. Fractals 2006, 14, 171–177. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Niccolini, G.; Puzzi, S. Morphological fractal dimension versus power-law exponent in the scaling of damaged media. Int. J. Damage Mech. 2009, 18, 259–282. [Google Scholar] [CrossRef]
- Li, W.; Kou, L.; Sun, M.; Wang, Y.; Shi, X.; Liang, H. Fractal analysis of effective permeability for power-law fluid in porous media with effective pore radius. Arab. J. Sci. Eng. 2024, 49, 9747–9756. [Google Scholar] [CrossRef]
- Liu, S.; Qiao, J.; Zeng, J.; Li, C.; Liu, Y.; Kong, Z.; Liu, X. Heterogeneity of Micro-and Nanopore Structure of Lacustrine Shales with Complex Lamina Structure. Fractal Fract. 2024, 8, 245. [Google Scholar] [CrossRef]
- Zhu, Z.; Fu, Q.; Hu, Z.; Duan, H.; Yang, B.; Xing, L.; Chen, G. Pore Structure and Heterogeneity in the Lacustrine Shale of the Second Member of the Paleogene Funing Formation, Subei Basin, China. Minerals 2024, 14, 1248. [Google Scholar] [CrossRef]
- La Pointe, P.R. Estimation of undiscovered hydrocarbon potential through fractal geometry. In Fractals in Petroleum Geology and Earth Processes; Springer: Boston, MA, USA, 1995; pp. 35–57. [Google Scholar] [CrossRef]
- Sheng, G.; Su, Y.; Wang, W.; Javadpour, F.; Tang, M. Application of fractal geometry in evaluation of effective stimulated reservoir volume in shale gas reservoirs. Fractals 2017, 25, 1740007. [Google Scholar] [CrossRef]
- Barton, C.A.; Zoback, M.D. Self-similar distribution and properties of macroscopic fractures at depth in crystalline rock in the Cajon Pass Scientific Drill Hole. Geophys. Res. Solid Earth 1992, 97, 5181–5200. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, S.; Wang, J.; Hu, Q.; Wang, M.; Chao, J. Applying fractal theory to characterize the pore structure of lacustrine shale from the Zhanhua Depression in Bohai Bay Basin, Eastern China. Energy Fuels 2018, 32, 7539–7556. [Google Scholar] [CrossRef]
- Katz, A.J.; Thompson, A.H. Fractal sandstone pores: Implications for conductivity and pore formation. Phys. Rev. Lett. 1985, 54, 1325. [Google Scholar] [CrossRef]
- Wong, P.Z.; Howard, J.; Lin, J.S. Surface roughening and the fractal nature of rocks. Phys. Rev. Lett. 1986, 57, 637. [Google Scholar] [CrossRef]
- Pfeifer, P.; Liu, K.Y. Multilayer adsorption as a tool to investigate the fractal nature of porous adsorbents. Stud. Surf. Sci. Catal. 1997, 104, 625–677. [Google Scholar] [CrossRef]
- Song, N.; Wang, T.G.; Liu, D.Y.; Gao, D.Q. Application of fractal methods to petroleum resource assessment in the Jinhu Depression, Subei Basin. Geol. Sci. 2006, 41, 578–585. [Google Scholar]
- Guo, Q.L.; Xie, H.B.; Mi, S.Y.; Chen, N.S.; Liang, K.; Hu, S.Y. Fractal characteristics of hydrocarbon resource distribution and its applications. Acta Pet. Sin. 2009, 30, 379–385. [Google Scholar]
- Dashtian, H.; Jafari, G.R.; Sahimi, M.; Masihi, M. Scaling, multifractality, and long-range correlations in well log data of large-scale porous media. Physica A 2011, 390, 2096–2111. [Google Scholar] [CrossRef]
- Babadagli, T.; Ren, X.; Develi, K. Effects of fractal surface roughness and lithology on single and multiphase flow in a single fracture: An experimental investigation. Int. J. Multiph. Flow 2015, 68, 40–58. [Google Scholar] [CrossRef]
- Ji, G.; Yang, Z.; Li, X.; Lu, Y.; Luo, D. A Model of the Fractal Fluid Loss Coefficient and its Effect on Fracture Length and Well Productivity. Chem. Technol. Fuels Oils 2015, 51, 168–180. [Google Scholar] [CrossRef]
- Jiang, F.; Chen, D.; Chen, J.; Li, Q.; Liu, Y.; Shao, X.; Hu, T.; Dai, J. Fractal analysis of shale pore structure of continental gas shale reservoir in the Ordos Basin, NW China. Energy Fuels 2016, 30, 4676–4689. [Google Scholar] [CrossRef]
- Liu, K.; Ostadhassan, M. Quantification of the microstructures of Bakken shale reservoirs using multi-fractal and lacunarity analysis. Nat. Gas Sci. Eng. 2017, 39, 62–71. [Google Scholar] [CrossRef]
- Cheng, H.; Jin, Z.K.; Yu, W.D.; Li, B.Q.; Zhu, X.E.; Chen, B.; Wu, Z.Z. Reservoir Classification and Evaluation Based on Fractal Theory and Factor Analysis: A case study of the Third member of the Funing Formation, Qintong Sag, Subei Basin. Acta Sedimentol. Sin. 2023, 41, 828–838. [Google Scholar]
- Lu, C.; Wang, X.; Ma, S.; Li, S.; Xue, T.; Li, Q. The Classification and Evaluation of an Interlayer Shale Oil Reservoir Based on the Fractal Characteristics of Pore Systems: A Case Study in the HSN Area, China. Fractal Fract. 2024, 8, 167. [Google Scholar] [CrossRef]
- Meneley, R.A.; Calverley, A.E.; Logan, K.G.; Procter, R.M. Resource assessment methodologies: Current status and future direction. AAPG Bull. 2003, 87, 535–540. [Google Scholar] [CrossRef]
- Guo, Q.; Chen, N.; Liu, C.; Xie, H.; Wu, X.; Wang, S.; Hu, J.; Gao, R. Research advance of hydrocarbon resource assessment method and a new assessment software system. Acta Pet. Sin. 2015, 36, 1305. [Google Scholar] [CrossRef]
- Qu, Y.; Chen, F.; Ma, L.; Jiang, P.; Li, B.; Ren, J.; Lv, R.; Liu, G.; Song, Z.; Chang, P.; et al. Fractal Characterization of a Multi-Scale Pore Structure in Ultra-Deep Coal Seams. Fractal Fract. 2025, 9, 250. [Google Scholar] [CrossRef]
- Guan, Q.; Dong, D.; Deng, B.; Chen, C.; Li, C.; Jiao, K.; Ye, Y.; Liang, H.; Yue, H. Structure and Fractal Characteristics of Organic Matter Pores in Wufeng-Lower Longmaxi Formations in Southern Sichuan Basin, China. Fractal Fract. 2025, 9, 410. [Google Scholar] [CrossRef]
- Wang, W.; Su, Y.; Sheng, G.; Cossio, M.; Shang, Y. A mathematical model considering complex fractures and fractal flow for pressure transient analysis of fractured horizontal wells in unconventional reservoirs. J. Nat. Gas Sci. Eng. 2015, 23, 139–147. [Google Scholar] [CrossRef]
- Zhang, M.; Jia, A.; Lei, Z.; Lei, G.A. Comprehensive Asset Evaluation Method for Oil and Gas Projects. Processes 2023, 11, 2398. [Google Scholar] [CrossRef]
- Song, X.; Feng, C.; Li, T.; Zhang, Q.; Pan, X.; Sun, M.; Ge, Y. Quantitative classification evaluation model for tight sandstone reservoirs based on machine learning. Sci. Rep. 2024, 14, 20712. [Google Scholar] [CrossRef]
- Cheng, Z.H.; Li, W.H.; Xue, H.T.; Lu, S.F.; Tan, Z.Z. Classification and evaluation criteria for tight sandstone reservoirs based on high-pressure mercury injection technology and fractal theory. J. Northeast. Pet. Univ. 2019, 43, 50–59+8. [Google Scholar]
- Shi, Y.H. Application of fractal theory in tight oil reservoir classification: A case study of lacustrine carbonate rocks in Leijia area, Liaohe Basin. Neijiang Sci. Technol. 2023, 44, 22–23. [Google Scholar]
- Li, S.; Bian, H.; Zhang, D.; Liu, Y.; Liu, G.; Wang, F. Research on pore structure and classification evaluation of tight oil reservoirs based on fractal theory. Acta Geophys. 2024, 72, 4079–4089. [Google Scholar] [CrossRef]
- Yang, B.; Wu, H.; Peng, M. Deep Sandstone Reservoir Characteristics and Pore Structure Classification Based on Fractal Theory: A Case Study of the Bayingobi Formation in Guaizihu Sag, Yin’e Basin. ACS Omega 2024, 9, 16976–16991. [Google Scholar] [CrossRef]
- Hazra, B.; Wood, D.A.; Vishal, V.; Varma, A.K.; Sakha, D.; Singh, A.K. Porosity controls and fractal disposition of organic-rich Permian shales using low-pressure adsorption techniques. Fuel 2018, 220, 837–848. [Google Scholar] [CrossRef]
- Bogahawaththa, M.; Mohotti, D.; Hazell, P.J.; Wang, H.; Wijesooriya, K.; Lee, C.K. Effect of fractal dimension on mechanical behaviour and energy absorption of Menger sponge-inspired fractal structures. Thin Wall. Struct. 2025, 206, 112704. [Google Scholar] [CrossRef]
- Wang, W.; Lin, C.; Zhang, X. Fractal Characteristics of Pore Throat and Throat of Tight Sandstone Sweet Spot: A Case Study in the East China Sea Basin. Fractal Fract. 2024, 8, 684. [Google Scholar] [CrossRef]
- Zhang, J. Characterization of shale pore structure combining fractal theory and method of moments. Complex Hydrocarb. Reserv. 2022, 15, 53–60. [Google Scholar] [CrossRef]
- Chen, F.Y.; Zhou, Y.; Yang, D.J.; Wan, H.F. Fractal-based study on pore structure of tight sandstone reservoirs: A case study of Yanchang Formation Chang 7 member in Qingcheng area, Ordos Basin. J. China Univ. Min. Technol. 2022, 51, 941–955. [Google Scholar] [CrossRef]
- Miao, T.; Yang, S.; Long, Z.; Yu, B. Fractal analysis of permeability of dual-porosity media embedded with random fractures. Int. J. Heat Mass Transf. 2015, 88, 814–821. [Google Scholar] [CrossRef]
- Cheng, Y.; Luo, X.; Zhuo, Q.; Gong, Y.; Liang, L. Description of pore structure of carbonate reservoirs based on fractal dimension. Processes 2024, 12, 825. [Google Scholar] [CrossRef]
- Li, J.H.; Zheng, B. Reconstruction Method of Digital Core and Pore Network Model Based on Stochastic Fractal Theory. CN104573198B, 15 August 2017. [Google Scholar]
- Guan, W.; Cai, W.; Li, Z.; Lu, H. Microscopic Characterization and Fractal Analysis of Pore Systems for Unconventional Reservoirs. J. Mar. Sci. Eng. 2024, 12, 908. [Google Scholar] [CrossRef]
- Wang, T.; Jiang, Y.Q.; Yang, C.C.; Wang, Z.L.; Zhu, X.; Pan, H.; Zhou, Y.D.; Yuan, Y.L.; He, Y. Pore structure and fluid movability of the tight sandstone reservoir in the Tianfu Gas Area of the Sichuan Basin. Sci. Technol. Eng. 2025, 25, 4900–4912. [Google Scholar]
- Wang, H.; Wu, W.; Chen, T.; Yu, J.; Pan, J. Pore structure and fractal analysis of shale oil reservoirs: A case study of the Paleogene Shahejie Formation in the Dongying Depression, Bohai Bay, China. J. Petrol. Sci. Eng. 2019, 177, 711–723. [Google Scholar] [CrossRef]
- Yu, B. Analysis of flow in fractal porous media. Appl. Mech. Rev. 2008, 61, 050801. [Google Scholar] [CrossRef]
- Wang, J.; Wei, Y.; Qi, Y. Semi-analytical modeling of flow behavior in fractured media with fractal geometry. Transp. Porous Media 2016, 112, 707–736. [Google Scholar] [CrossRef]
- Xia, Y.X. Fractal Characterization of Micro-Pore Structure and Seepage Characteristics in Low-Permeability Reservoirs. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2022. [Google Scholar] [CrossRef]
- Wang, G. Development of a Relative Permeability Prediction Model Based on Fractal Theory. Master’s Thesis, China University of Petroleum, Beijing, China, 2022. [Google Scholar] [CrossRef]
- Wang, S.F.; Wu, T.; Deng, Y.J.; Zheng, Q.S. A new fractal model for permeability of porous media. Chin. Q. Mech. 2016, 37, 293–301. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Xue, H.; Shen, Z.; Chen, L. Fractal characteristics of shale pore structure and its influence on seepage flow. R. Soc. Open Sci. 2021, 8, 202271. [Google Scholar] [CrossRef]
- Zhou, Z.; Su, Y.; Wang, W.; Yan, Y. Application of the fractal geometry theory on fracture network simulation. J. Pet. Explor. Prod. Technol. 2017, 7, 487–496. [Google Scholar] [CrossRef]
- Wang, W.D.; Su, Y.L.; Zhang, Q.; Xiang, G.; Cui, S.M. Performance-based fractal fracture model for complex fracture network simulation. Pet. Sci. 2018, 15, 126–134. [Google Scholar] [CrossRef]
- Hirata, T. Fractal dimension of fault systems in Japan: Fractal structure in rock fracture geometry at various scales. Pure Appl. Geophys. 1989, 131, 157–170. [Google Scholar] [CrossRef]
- Hu, B.; Wang, J.; Ma, Z. A fractal discrete fracture network based model for gas production from fractured shale reservoirs. Energies 2020, 13, 1857. [Google Scholar] [CrossRef]
- Li, X.Y. Establishment of a rough fracture model based on fractal theory and its impact on proppant transport. Chem. Eng. Manag. 2024, 74–77. [Google Scholar] [CrossRef]
- Su, X. Flow Analysis in Fractured-Vuggy Carbonate Reservoirs Based on Fractal Theory. Master’s Thesis, China University of Petroleum (East China), Dongying, China, 2022. [Google Scholar] [CrossRef]
- He, Q. Effectiveness of Hydraulic Fracture Networks in Oil Shale Based on Fractal and Topological Analysis. Master’s Thesis, Sichuan University, Chengdu, China, 2021. [Google Scholar] [CrossRef]
- Wadood, A.; Yousaf, A.F.; Alatwi, A.M. An Enhanced Multiple Unmanned Aerial Vehicle Swarm Formation Control Using a Novel Fractional Swarming Strategy Approach. Fractal Fract. 2024, 8, 334. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Q.; Lyu, Q.; Xue, Z.; Cao, X.; Liu, Z. Evaluation technology and practice of continental shale oil development in China. Pet. Explor. Dev. 2022, 49, 1098–1109. [Google Scholar] [CrossRef]
- Watanabe, K.; Takahashi, H. Parametric study of the energy extraction from hot dry rock based on fractal fracture network model. Geothermics 1995, 24, 223–236. [Google Scholar] [CrossRef]
- Ren, Q.; Gao, T.; Jiang, R.; Wang, J.; Li, M.; Feng, J.; Du, H. Fractal-Fractional Synergy in Geo-Energy Systems: A Multiscale Framework for Stress Field Characterization and Fracture Network Evolution Modeling. Fractal Fract. 2025, 9, 322. [Google Scholar] [CrossRef]


| No. | Dimension | Traditional Methods (Volumetric/Statistical Approaches) | Fractal Theory | References |
|---|---|---|---|---|
| 1 | Theoretical Foundation | Euclidean geometry (regular shapes), linear statistical models, reservoir homogeneity assumptions | Fractal geometry (self-similarity, scale invariance), nonlinear theory | Adapted from [26,27] |
| 2 | Core Assumptions | Reservoir homogeneity, regular geometric forms (e.g., cubic sand bodies, cylindrical traps) | Reservoir heterogeneity, cross-scale complex structures (pores-fractures-traps) | Adapted from [38] |
| 3 | Data Dependency | Limited exploration data (well points, 2D seismic profiles) | Multi-scale digital data (CT scans, FIB-SEM 3D reconstruction) | Adapted from [59,60] |
| 4 | Characterization Capability | Qualitative descriptions dominate, limited ability to quantify heterogeneity | Quantitative parameters: fractal dimension (D), multifractal spectrum width (Quantifies the fluctuations in heterogeneity within complex systems) (Δα) | Adapted from [34,35] |
| 5 | Typical Limitations | Fails to capture nano-pore complexity in shale; lacks patterns for subtle reservoir distribution | Nano-pore fractal dimension D = 2.5–3.0; Fracture network multifractal spectrum width Δα = 0.3–0.6 | Adapted from [38,39] |
| 6 | Engineering Application | Empirical fracturing design; SRV evaluation ignores fracture network connectivity | Fractal dimension correlated with brittleness index to optimize fracturing parameters | Adapted from [38] |
| 7 | Applicable Scenarios | Conventional reservoirs with strong homogeneity (e.g., high-permeability sandstone) | Unconventional reservoirs with strong heterogeneity (shale gas, tight oil), fractured reservoirs (carbonate) | Adapted from [40] |
| No. | Assessment Aspect | Key Progress | Outstanding Challenges |
|---|---|---|---|
| 1 | Reservoir classification and evaluation | Quantified correlations between fractal dimension and porosity/permeability enable robust reservoir typing and sweet spot identification. Higher fractal dimensions reliably indicate stronger heterogeneity | Limited integration of dynamic production data; absence of universal classification standards across different geological regions |
| 2 | Pore structure characterization | Fractal dimensions from multi-source data (e.g., MIP, SEM) effectively quantify pore complexity and connectivity, improving digital rock model accuracy | Models are predominantly static; lack of dynamic coupling between fractal parameters and reservoir performance during production |
| 3 | Seepage behavior analysis | Fractal capillary models accurately predict key parameters (e.g., permeability), with errors <5%, and clarify flow mechanisms in nanoscale pores | Poor performance for transient multiphase flow; high computational cost for complex fractal model solutions |
| 4 | Fracture network modeling and evaluation | Fractal dimensions (box-counting, etc.) quantify network complexity; DFN models reveal links between fractal geometry, productivity, and stimulation design | Idealized model assumptions mismatch real fracture geometry; inability to simulate dynamic fracture evolution under changing field stresses |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Zhang, X.; Zou, C.; Zhao, L.; He, H. Advances in the Application of Fractal Theory to Oil and Gas Resource Assessment. Fractal Fract. 2025, 9, 676. https://doi.org/10.3390/fractalfract9100676
Liu B, Zhang X, Zou C, Zhao L, He H. Advances in the Application of Fractal Theory to Oil and Gas Resource Assessment. Fractal and Fractional. 2025; 9(10):676. https://doi.org/10.3390/fractalfract9100676
Chicago/Turabian StyleLiu, Baolei, Xueling Zhang, Cunyou Zou, Lingfeng Zhao, and Hong He. 2025. "Advances in the Application of Fractal Theory to Oil and Gas Resource Assessment" Fractal and Fractional 9, no. 10: 676. https://doi.org/10.3390/fractalfract9100676
APA StyleLiu, B., Zhang, X., Zou, C., Zhao, L., & He, H. (2025). Advances in the Application of Fractal Theory to Oil and Gas Resource Assessment. Fractal and Fractional, 9(10), 676. https://doi.org/10.3390/fractalfract9100676






