Solving Fully Intuitionistic Fuzzy Multi-Level Multi-Objective Fractional Optimization Problems via Two Different Approaches
Abstract
1. Introduction
Motivation
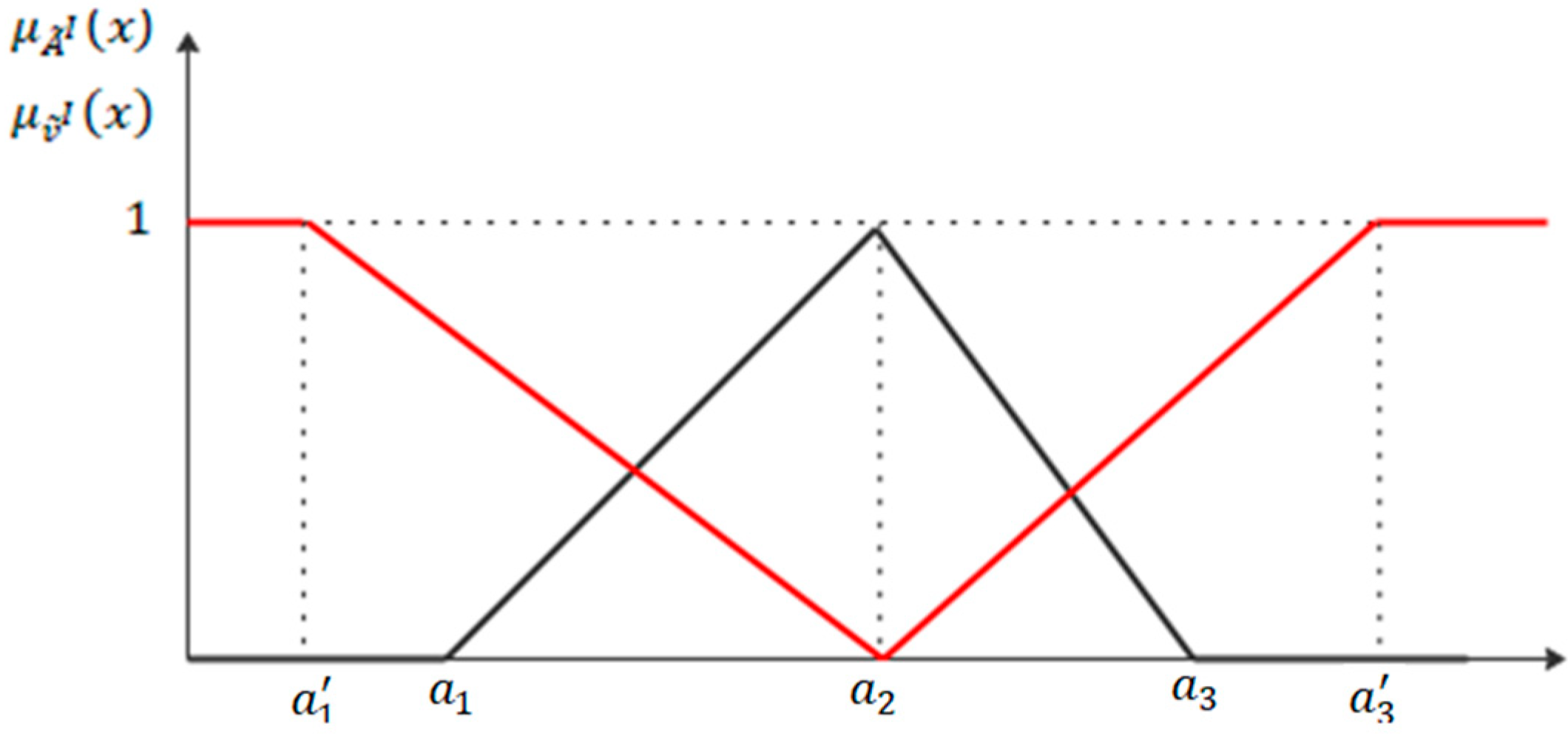
2. Preliminaries
3. Mathematical Formulation
Non-Fractional Model Development
4. Deterministic Model Formulation
5. Interactive Approach to FIF-MLMOFPP
5.1. FLDM -Constraint Model
| Algorithm 1. Solution for the FLDM | |
| Step 1. | Assign the satisfactoriness . Let initially and let consequently. |
| Step 2. | Adjust the -constraint model if has no solution or has an optimal solution with , then go to Step 1, to adjust . If not, proceed to Step 3. |
| Step 3. | If the DM is satisfied with , then it is the preferred solution of the LDM, go to Step 5. If not, proceed to Step 4. |
| Step 4. | Modify satisfactoriness, let and go to step 2. |
| Step 5. | Stop. |
5.2. SLDM -Constraint Model
5.3. -constraint model
5.4. Interactive Algorithm for FIF-MLMOFPP
| Step 1. | Set up the non-fractional model, Equations (19)–(24), of FIF-MLMOFPP. |
| Step 2. | Apply the ranking functions and ordering relations to set up the deterministic model, Equations (31)–(34). |
| Step 3. | Compute the individual maximum and minimum values of each objective. |
| Step 4. | Set . |
| Step 5. | Follow the instructions in Algorithm I to generate a list of the FLDM problem’s preferred solutions. The following format is used by the FLDM to arrange these solutions: Preferred solution Preferred ranking |
| Step 6. | Given to the SLDM issue. Solve the SLDM issue to obtain |
| Step 7. | If then go to Step 8. Otherwise go to Step 11. |
| Step 8. | Given to the LDM issue, solve the LDM issue following Algorithm I to obtain |
| Step 9. | If then go to Step 10. If not go to Step 11. |
| Step 10. | If the FLDM is pleased with and , then is the preferred solution of the FIF-MLMOFPP, go to Step 12. If not go to Step 11. |
| Step 11. | Let and go to Step 6. |
| Step 12. | Stop. |
6. Neutrosophic Fuzzy Goal Programming Approach
NFGP Algorithms for FIF-MLMOFPP
| Step 1. | Formulate the non-fractional model, Equations (19)–(24), of FIF-MLMOFPP. |
| Step 2. | Apply the ranking functions and ordering relations to set up the deterministic model, Equations (31)–(34). |
| Step 3. | Determine the distinct maximum and lowest values for each goal function. |
| Step 4. | Construct the different membership functions Equations (55)–(57). |
| Step 5. | Set up the numerical weights Equation (64). |
| Step 6. | Construct and solve the final NFGP model (58)–(63). |
7. Illustrative Example
7.1. Solution Based on Interactive Approach
| Intuitionistic Fuzzy Solution | Intuitionistic Objective Value |
7.2. Solution Based on NFGP Approach
8. Discussion
- -
- The proposed multi-level fractional optimization modeling approach handles intuitionistic fuzzy parameters, which involve membership as well as non-membership functions and are more realistic compared to fuzzy parameters;
- -
- The proposed NFGP approach addresses the indeterminacy degree, which is the area of uncertainty between the acceptance and rejection degrees of propositions.
- -
- The proposed model is able to handle the FIF-MLMOFPP because it is a simple concept, easy to implement, requires less execution effort, and is more flexible and adaptive to a wide variety of problems.
- -
- It can be easily implemented in different real-life problems, such as transportation, supplier selection, supply chain, manufacturing, inventory control, assignment problems, etc.
9. Conclusions
- -
- Multi-choice rough fractional ML-MOOP models utilizing the interactive approach;
- -
- Fully intuitionistic fuzzy fractional bi-level production planning models;
- -
- Intuitionistic fuzzy bi-level supply chain models using the NFGP approach.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FIF-MLMOFPP | Fully intuitionistic fuzzy multi-level multi-objective fractional programming problem |
| IFNs | Intuitionistic fuzzy numbers |
| FIF-MLMOPP | Fully intuitionistic fuzzy multi-level multi-objective programming problem |
| MOOP | Multi-objective optimization problem |
| NFGP | Neutrosophic fuzzy goal programming |
| DMs | Decision makers |
| ML-MOOPs | Multi-level multi-objective optimization problems |
| FST | Fuzzy set theory |
| FLDM | First-level decision maker |
| BLOPs | Bi-level programming problems |
| FGP | Fuzzy goal programming |
| IFS | Intuitionistic fuzzy sets |
| NS | Neutosophic sets |
| TIFN | Triangular intuitionistic fuzzy number |
| SLDM | Second-level decision maker |
| KLDM | K-level decision maker |
| TOPSIS | Technique of Order Preferences by Similarity to Ideal Solution |
References
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Singh, V.P.; Sharma, K.; Chakraborty, D.; Ebrahimnejad, A. A novel multi-objective bi-level programming problem under intuitionistic fuzzy environment and its application in production planning problem. Complex Intell. Syst. 2022, 8, 3263–3278. [Google Scholar] [CrossRef]
- Sharma, K.; Singh, V.P.; Ebrahimnejad, A.; Chakraborty, D. Solving a multi-objective chance constrained hierarchical optimization problem under intuitionistic fuzzy environment with its application. Expert Syst. Appl. 2023, 217, 119595. [Google Scholar] [CrossRef]
- Abo-Sinna, M.A.; Baky, I.A. Interactive balance space approach for solving multi-level multi-objective programming problems. Inf. Sci. 2007, 177, 3397–3410. [Google Scholar] [CrossRef]
- Abo-Elnagga, Y.; Elsisy, M.A.; El Sayed, M.A. A novel algorithm for generating Pareto frontier of bi-level multi-objective rough nonlinear programming problem. Ain Shams Eng. J. 2021, 12, 2125–2133. [Google Scholar]
- Baky, I.A. Solving multi-level multi-objective linear programming problems through fuzzy goal programming approach. Appl. Math. Model. 2010, 34, 2377–2387. [Google Scholar] [CrossRef]
- Osman, M.S.; Emam, O.E.; El Sayed, M.A. Interactive Approach for Multi-Level Multi-Objective Fractional Programming Problems with Fuzzy Parameters. Beni-Suef Univ. J. Basic Appl. Sci. 2018, 7, 139–149. [Google Scholar] [CrossRef]
- Pramanik, S.; Roy, T.K. Fuzzy goal programming approach to multi-level programming problems. Eur. J. Oper. Res. 2007, 176, 1151–1166. [Google Scholar] [CrossRef]
- Chen, L.H.; Chen, H.H. A two-phase fuzzy approach for solving multi-level decision-making problems. Knowl. Based Syst. 2015, 76, 189–199. [Google Scholar] [CrossRef]
- Lachhwani, K. Modified FGP approach for multi-level multi objective linear fractional programming problems. Appl. Math. Comput. 2015, 266, 1038–1049. [Google Scholar] [CrossRef]
- Osman, M.S.; Emam, O.E.; El Sayed, M.A. Stochastic fuzzy multi-level mutiobjective fractional programming problem: A FGP approach. OPSEARCH 2017, 54, 816–840. [Google Scholar] [CrossRef]
- Ren, A. A novel method for solving the fully fuzzy bi-level linear programming problem. Math. Prob. Eng. 2015, 2, 1–11. [Google Scholar]
- Baky, I.A. Fuzzy goal programming algorithm for solving decentralized bi-level multi-objective programming problems. Fuzzy Sets Systems 2009, 160, 2701–2713. [Google Scholar] [CrossRef]
- Baky, I.A.; Eid, M.H.; El Sayed, M.A. Bi-level multi-objective programming problem with fuzzy demands: A fuzzy goal programming algorithm. OPSEARCH 2014, 51, 280–296. [Google Scholar] [CrossRef]
- Arora, S.R.; Gupta, R. Interactive fuzzy goal programming approach for bi-level programming problem. Eur. J. Oper. Res. 2009, 194, 368–376. [Google Scholar] [CrossRef]
- Toksari, M.D.; Bilim, Y. Interactive fuzzy goal programming based on jacobian matrix to solve decentralized bi-level multi-objective fractional programming problems. Int. J. Fuzzy Syst. 2015, 17, 499–508. [Google Scholar] [CrossRef]
- Emam, O.E. Interactive approach to bi-level integer multi-objective fractional programming problem. Appl. Math. Comput. 2013, 233, 17–24. [Google Scholar] [CrossRef]
- Helmy, Y.M.; Emam, O.E.; Abdelwahab, A.M. On stochastic multi-level multiobjective fractional programming problems. J. Stat. Appl. Probab. 2015, 4, 93–101. [Google Scholar]
- El Sayed, M.A.; Baky, I.A.; Singh, P. A modified TOPSIS approach for solving stochastic fuzzy multi-level multi-objective fractional decision making problem. OPSEARCH 2020, 57, 1374–1403. [Google Scholar] [CrossRef]
- El Sayed, M.A.; Farahat, F.A.; Elsisy, M.A.; Alsabaan, M.; Ibrahem MIElwahsh, H. Two TOPSIS-Based Approaches for Multi-Choice Rough Bi-Level Multi-Objective Nonlinear Programming Problems. Mathematics 2025, 13, 1242. [Google Scholar] [CrossRef]
- Bhati, D.; Singh, P. Branch and bound computational method for multi-objective linear fractional optimization problem. Neural Comput. Appl. 2017, 28, 3341–3351. [Google Scholar] [CrossRef]
- AbdAlhakim, H.; Emam, O.E.; Abd El-Mageed, A.A. Architecting a fully fuzzy information model for multi-level quadratically constrained quadratic programming problem. OPSEARCH 2019, 56, 367–389. [Google Scholar] [CrossRef]
- Ahlatcioglu, M.; Tiryaki, F. Interactive fuzzy programming for decentralized two-level linear fractional programming problems. Omega 2007, 35, 432–450. [Google Scholar] [CrossRef]
- Emam, O.E.; El-Araby, M.; Belal, M.A. On Rough Multi-Level Linear Programming Problem. Inf. Sci. Lett. 2015, 4, 41–49. [Google Scholar]
- Nayak, S.; Ojha, A.K. An approach of fuzzy and TOPSIS to bi-level multi-objective nonlinear fractional programming problem. Soft Comput. 2019, 23, 5605–5618. [Google Scholar] [CrossRef]
- Abo-Sinna, M.A.; Amer, A.H. TOPSIS approach for solving bi-level non-linear fractional MODM problems. J. Adv. Math. 2018, 13, 7353–7370. [Google Scholar] [CrossRef]
- Guzel, N. A proposal to the solution of multi-objective linear fractional programming problem. Abstr. Appl. Anal. 2013, 2013, 435030. [Google Scholar] [CrossRef]
- Arya, R.; Singh, P.; Kumari, S.; Obaidat, M.S. An approach for solving fully fuzzy multi-objective linear fractional optimization problems. Soft Comput. 2019, 24, 9105–9119. [Google Scholar] [CrossRef]
- Angammal, S.; Hannah, G. A new bi-level TOPSIS based neutrosophic programming technique for land allocation to medium farm holders. Heliyon 2024, 10, e36166. [Google Scholar] [CrossRef]
- Ahmad, F.; Adhami, A.Y. Neutrosophic programming approach to multiobjective nonlinear transportation problem with fuzzy parameters. Int. J. Manag. Sci. Eng. Manag. 2019, 14, 218–229. [Google Scholar] [CrossRef]
- Ahmad, F.; Adhami, A.Y.; Smarandache, F. Single Valued Neutrosophic Hesitant Fuzzy Computational Algorithm for Multiobjective Nonlinear Optimization Problem. Neutrosophic Sets Syst. 2018, 22, 76–86. [Google Scholar]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic. In Philosophy; American Research Press: Champaign, IL, USA, 1999; pp. 1–141. [Google Scholar]
- Ahmad, F.; Adhami, A.Y.; Smarandache, F. Modified Neutrosophic Fuzzy Optimization Model for Optimal Closed-Loop Supply Chain Management Under Uncertainty. In Optimization Theory Based on Neutrosophic and Plithogenic Sets; Elsevier: Amsterdam, The Netherlands, 2020; pp. 343–403. [Google Scholar]
- Ahmad, S.; Ahmad, F.; Sharaf, M. Supplier selection problem with type-2 fuzzy parameters: A neutrosophic optimization approach. Int. J. Fuzzy Syst. 2021, 23, 755–775. [Google Scholar] [CrossRef]
- Almotairi, S.; Badr, E.; Elsisy, M.A.; Farahat, F.A.; El Sayed, M.A. Performance Analysis of Fully Intuitionistic Fuzzy Multi-Objective Multi-Item Solid Fractional Transportation Model. Fractal Fract. 2024, 8, 404. [Google Scholar] [CrossRef]
- Ahmad, F.; Ahmad, S.; Soliman, A.T.; Abdollahian, M. Solving multi-level multi-objective fractional programming problem with rough interval parameter in neutrosophic environment. RAIRO Oper. Res. 2021, 55, 2567–2581. [Google Scholar] [CrossRef]
- Ahmadini, A.A.H.; Ahmad, F. Solving intuitionistic fuzzy multiobjective linear programming problem under neutrosophic environment. AIMS Math. 2021, 6, 4556–4580. [Google Scholar] [CrossRef]
- Fathy, E.; Ammar, E.; Helmy, M.A. Fully intuitionistic fuzzy multi-level linear fractional programming problem. Alex. Eng. J. 2023, 77, 684–694. [Google Scholar] [CrossRef]
- El Sayed, M.A.; Abo-Sinna, M.A. A novel Approach for Fully Intuitionistic Fuzzy Multi-Objective Fractional Transportation Problem. Alex. Eng. J. 2021, 60, 1447–1463. [Google Scholar] [CrossRef]
- Mahajan, S.; Chauhan, A.; Gupta, S.K. On Pareto optimality using novel goal programming approach for fully intuitionistic fuzzy multiobjective quadratic problems. Expert Syst. Appl. 2024, 243, 122816. [Google Scholar] [CrossRef]
- Roy, S.K.; Ebrahimnejad, A.; Verdegay, J.L.; Das, S. New approach for solving intuitionistic fuzzy multi-objective transportation problem. Sadhana 2018, 43, 3. [Google Scholar] [CrossRef]
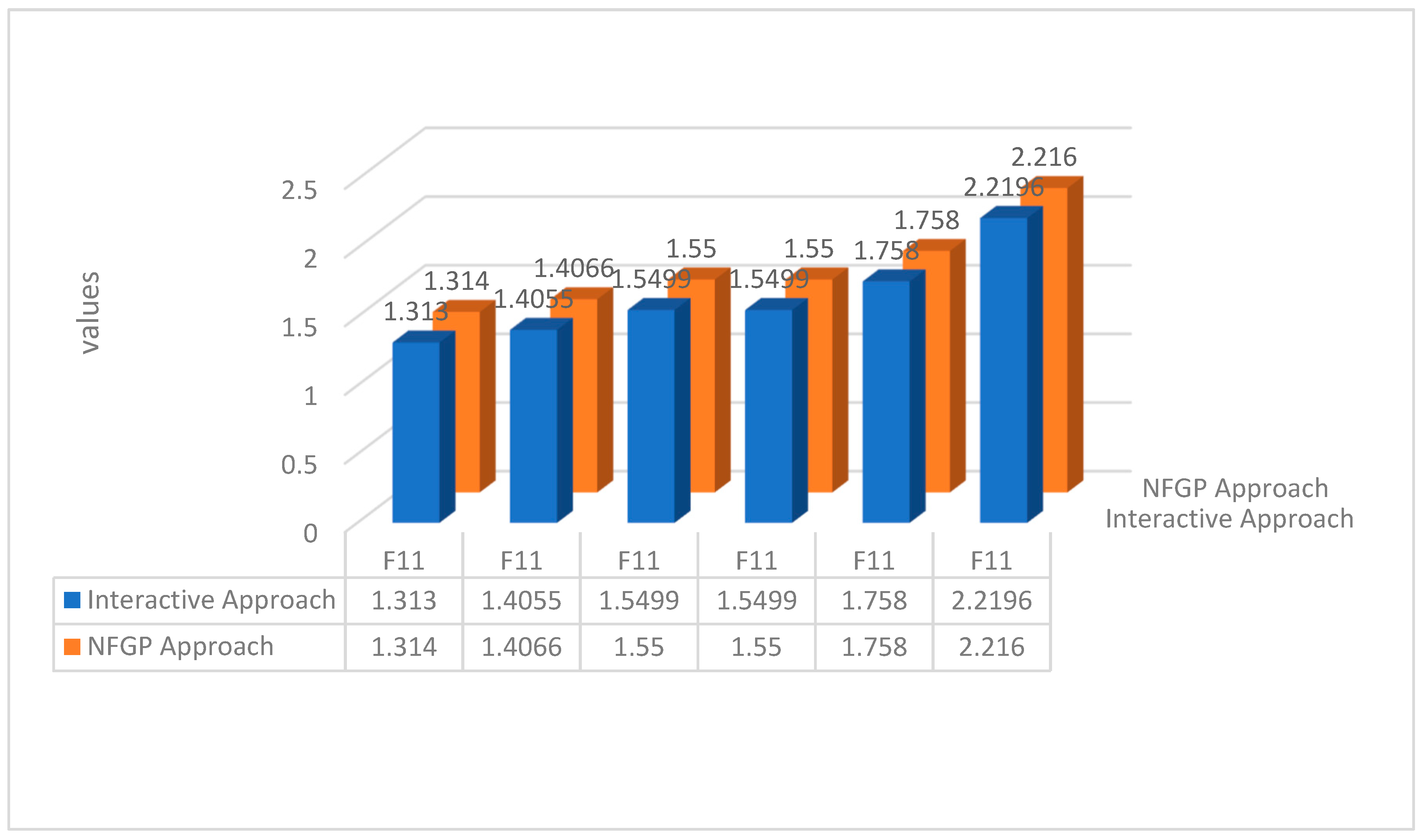
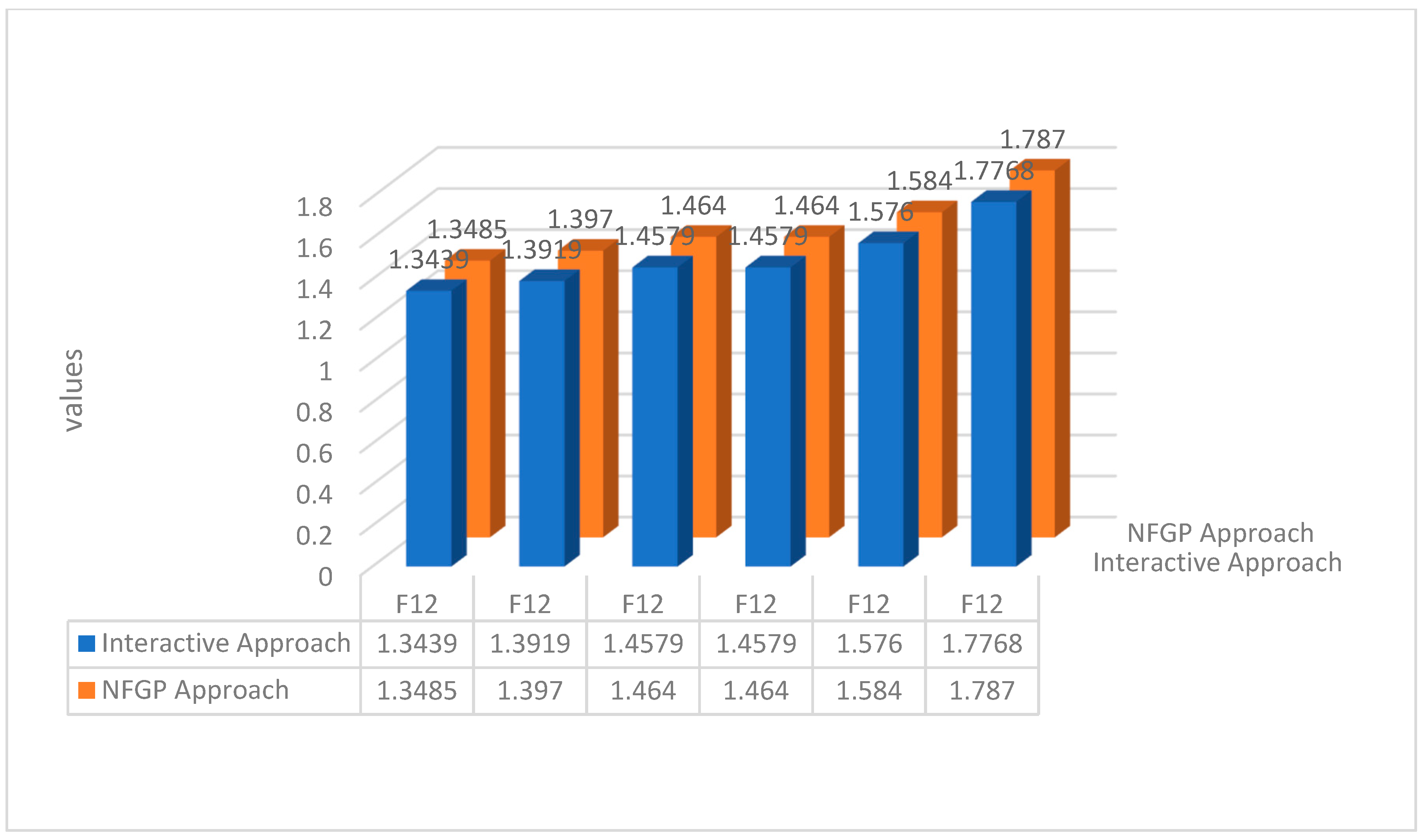
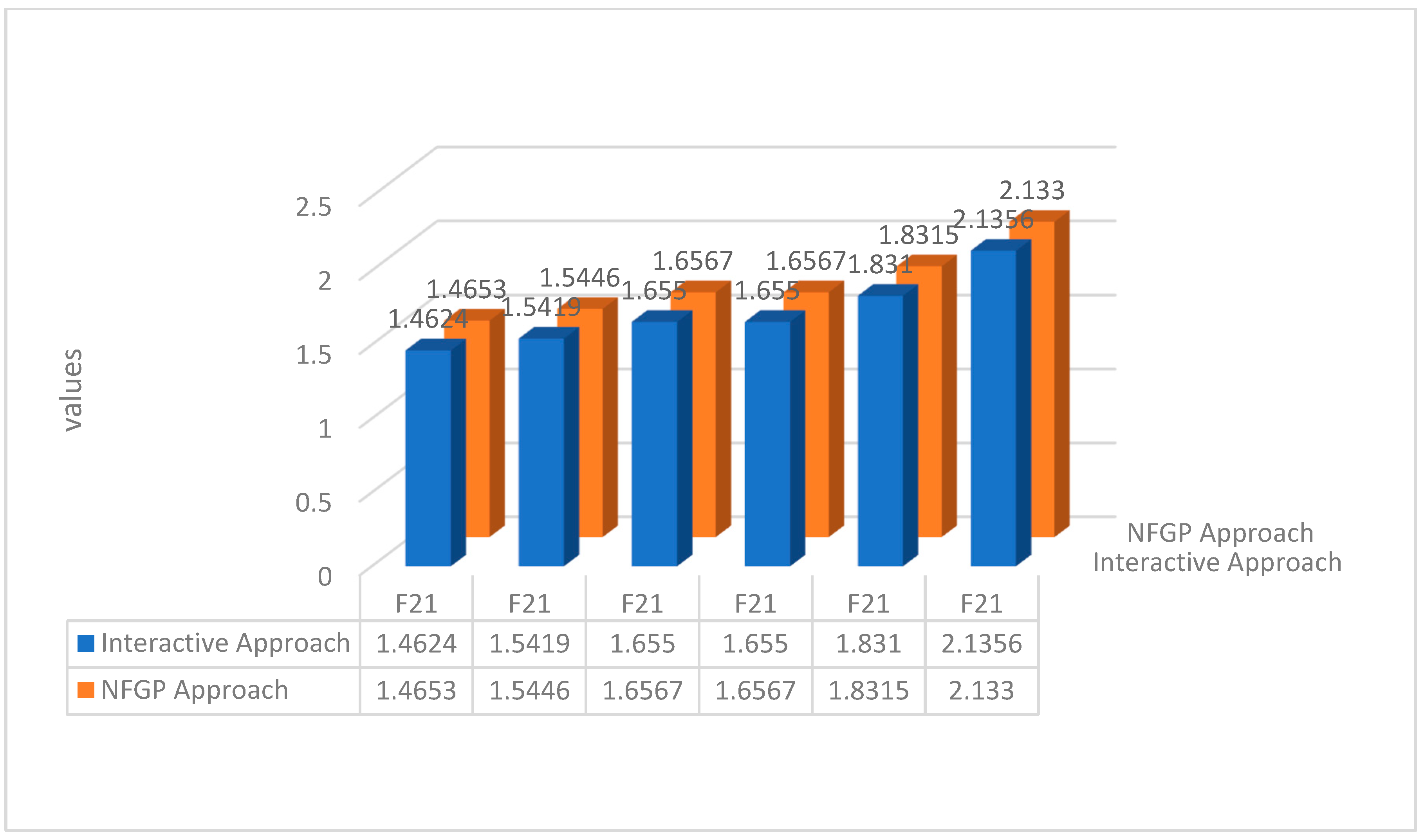
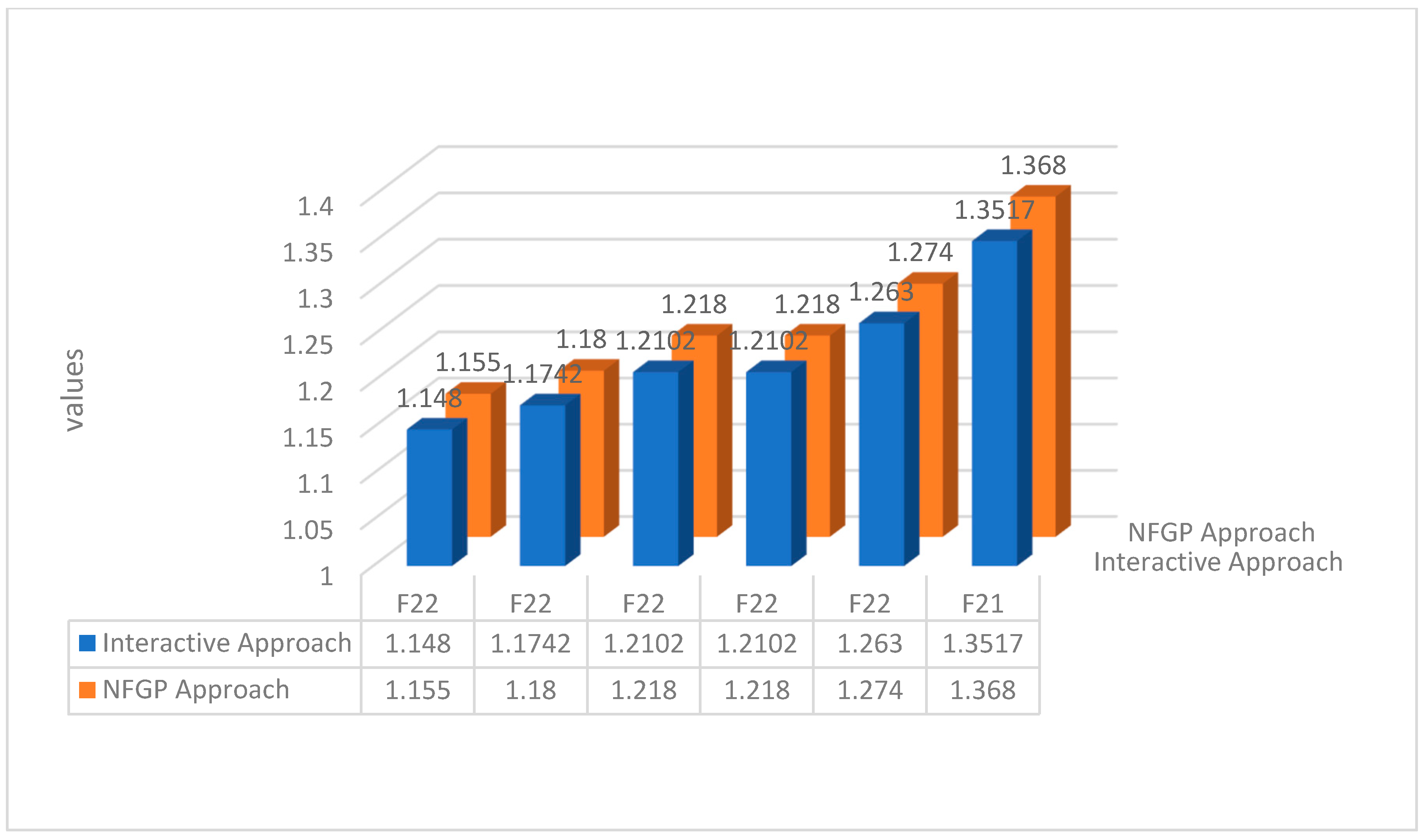
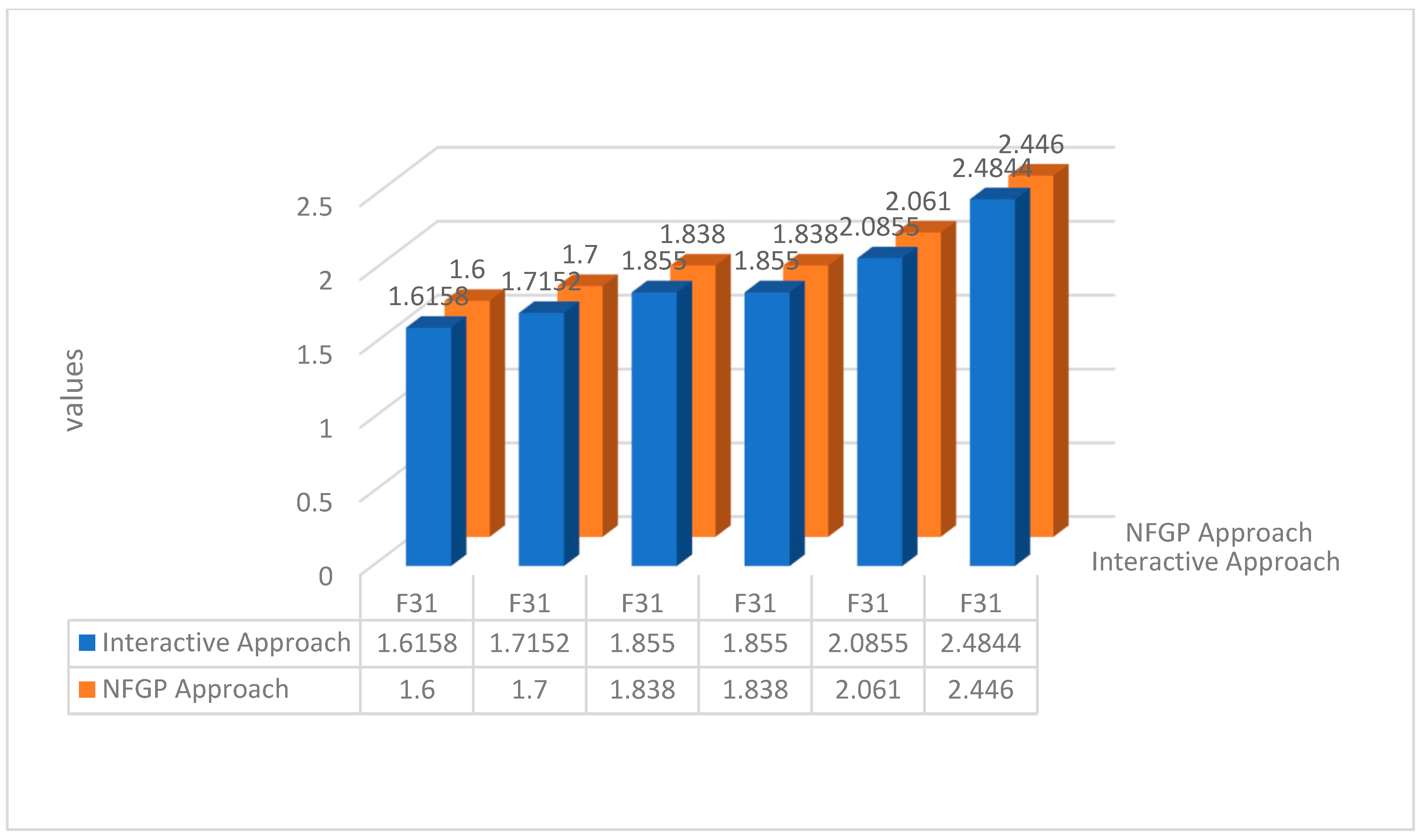

| 0.7944 | 1.026 | 1.139 | 0.9954 | 1.271 | 1.1759 | |
| 0.000158 | 0.000161 | 0.000194 | 0.000227 | 0.000199 | 0.000211 |
| Interactive Approach | NFGP Approach | |
|---|---|---|
| Total solver iteration | 20 | 16 |
| Elapsed runtime seconds | 0.10 | 0.13 |
| Model class | LP | LP |
| Total variables | 12 | 52 |
| Nonlinear variables | 0 | 0 |
| Integer variables | 0 | 0 |
| Total constraints | 68 | 107 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Sayed, M.A.; Elwahsh, H.; Hoxha, J.; Khalifa, T.; Farahat, F.A.; Elsisy, M.A.; Bukhari, F.A. Solving Fully Intuitionistic Fuzzy Multi-Level Multi-Objective Fractional Optimization Problems via Two Different Approaches. Fractal Fract. 2025, 9, 675. https://doi.org/10.3390/fractalfract9100675
El Sayed MA, Elwahsh H, Hoxha J, Khalifa T, Farahat FA, Elsisy MA, Bukhari FA. Solving Fully Intuitionistic Fuzzy Multi-Level Multi-Objective Fractional Optimization Problems via Two Different Approaches. Fractal and Fractional. 2025; 9(10):675. https://doi.org/10.3390/fractalfract9100675
Chicago/Turabian StyleEl Sayed, Mohamed A., Haitham Elwahsh, Julian Hoxha, Tarek Khalifa, Farahat A. Farahat, Mohamed A. Elsisy, and Fawzy A. Bukhari. 2025. "Solving Fully Intuitionistic Fuzzy Multi-Level Multi-Objective Fractional Optimization Problems via Two Different Approaches" Fractal and Fractional 9, no. 10: 675. https://doi.org/10.3390/fractalfract9100675
APA StyleEl Sayed, M. A., Elwahsh, H., Hoxha, J., Khalifa, T., Farahat, F. A., Elsisy, M. A., & Bukhari, F. A. (2025). Solving Fully Intuitionistic Fuzzy Multi-Level Multi-Objective Fractional Optimization Problems via Two Different Approaches. Fractal and Fractional, 9(10), 675. https://doi.org/10.3390/fractalfract9100675






