Finite-Time Synchronization and Mittag–Leffler Synchronization for Uncertain Fractional-Order Delayed Cellular Neural Networks with Fuzzy Operators via Nonlinear Adaptive Control
Abstract
1. Introduction
2. Fundamental Knowledge and Network Models
3. New Synchronization Results of UFODCNNs
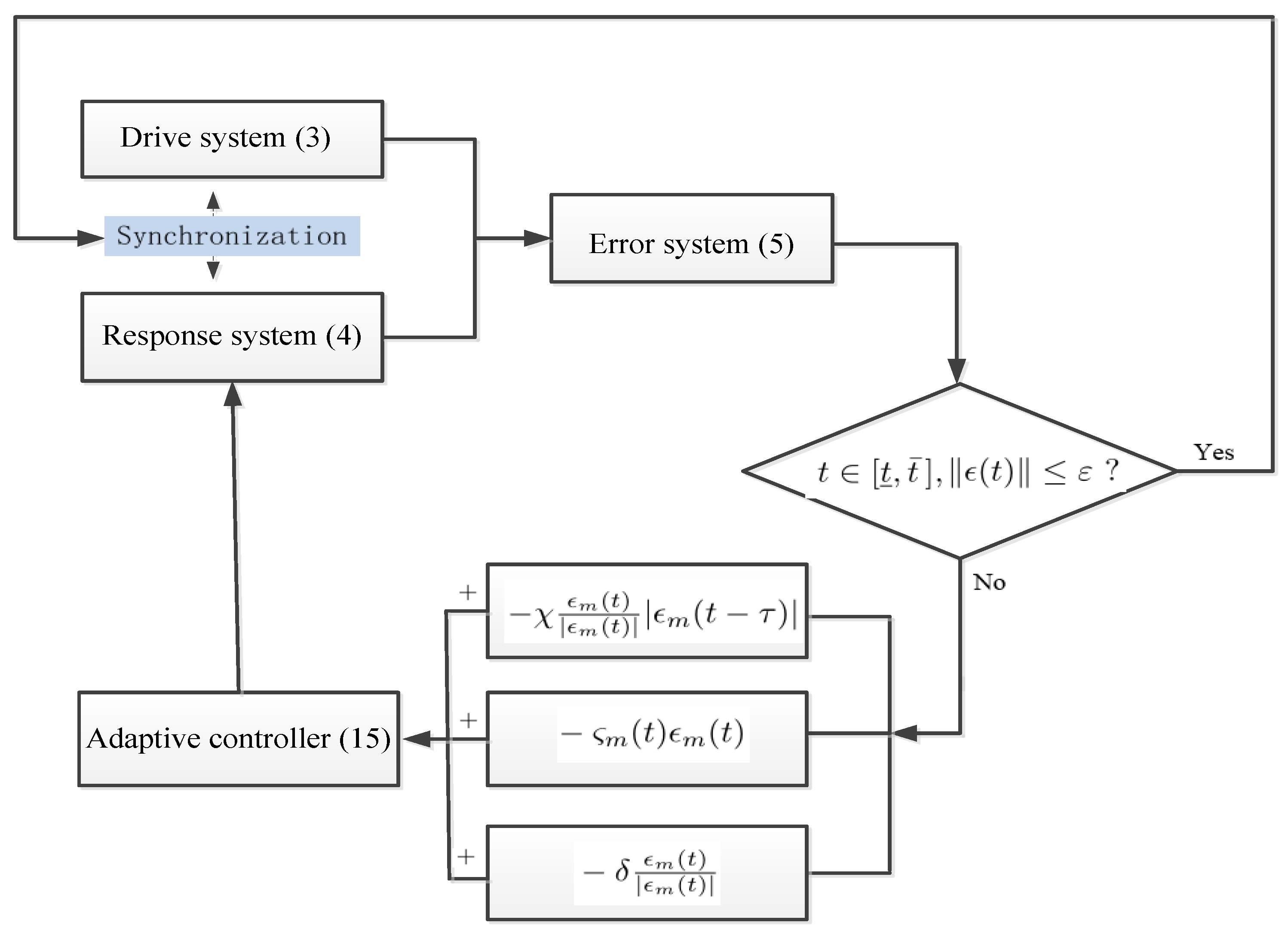
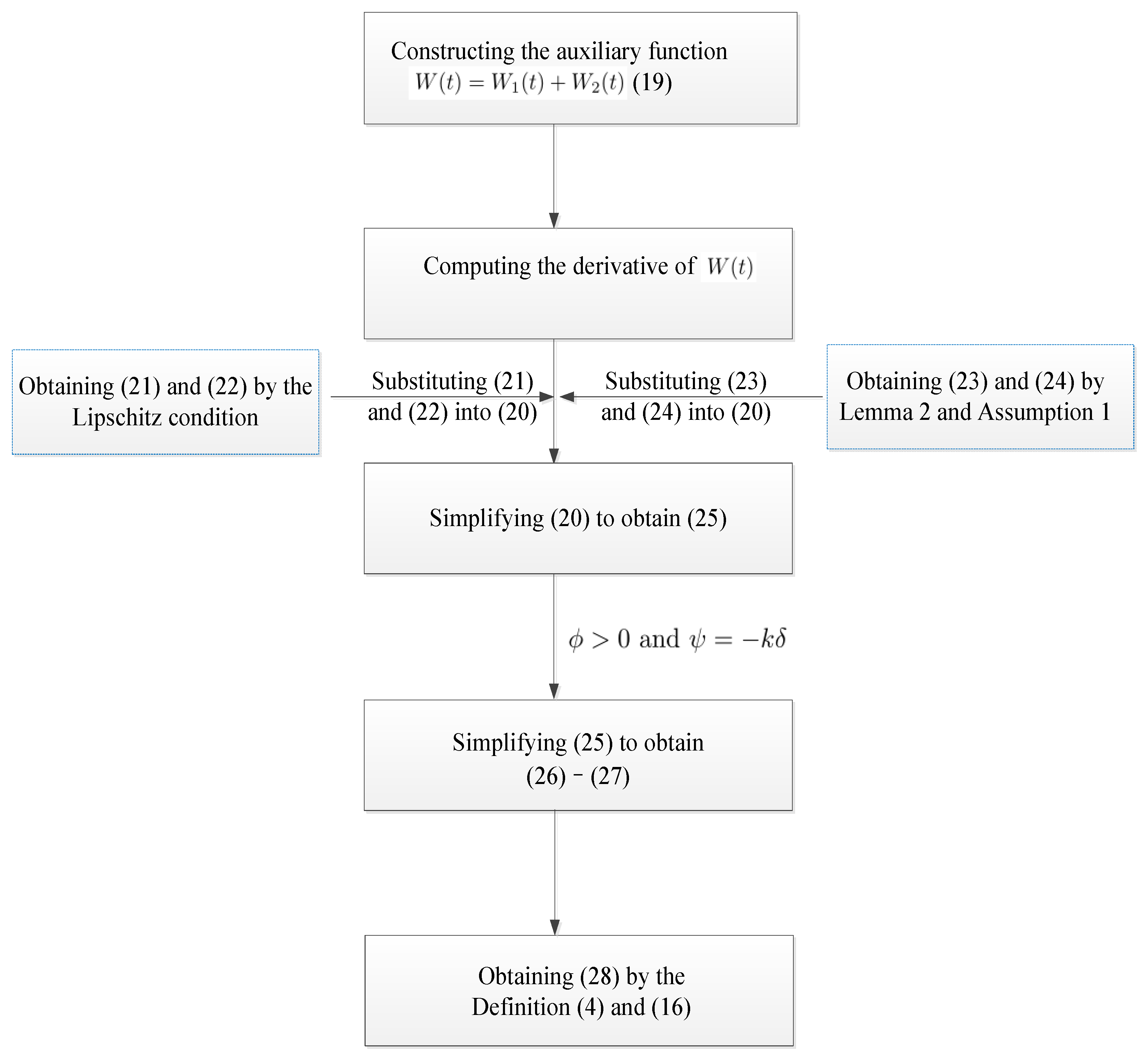
3.1. FT Synchronization Criteria
3.2. FT Mittag–Leffler Synchronization Criteria
3.3. FT Synchronization Corollary
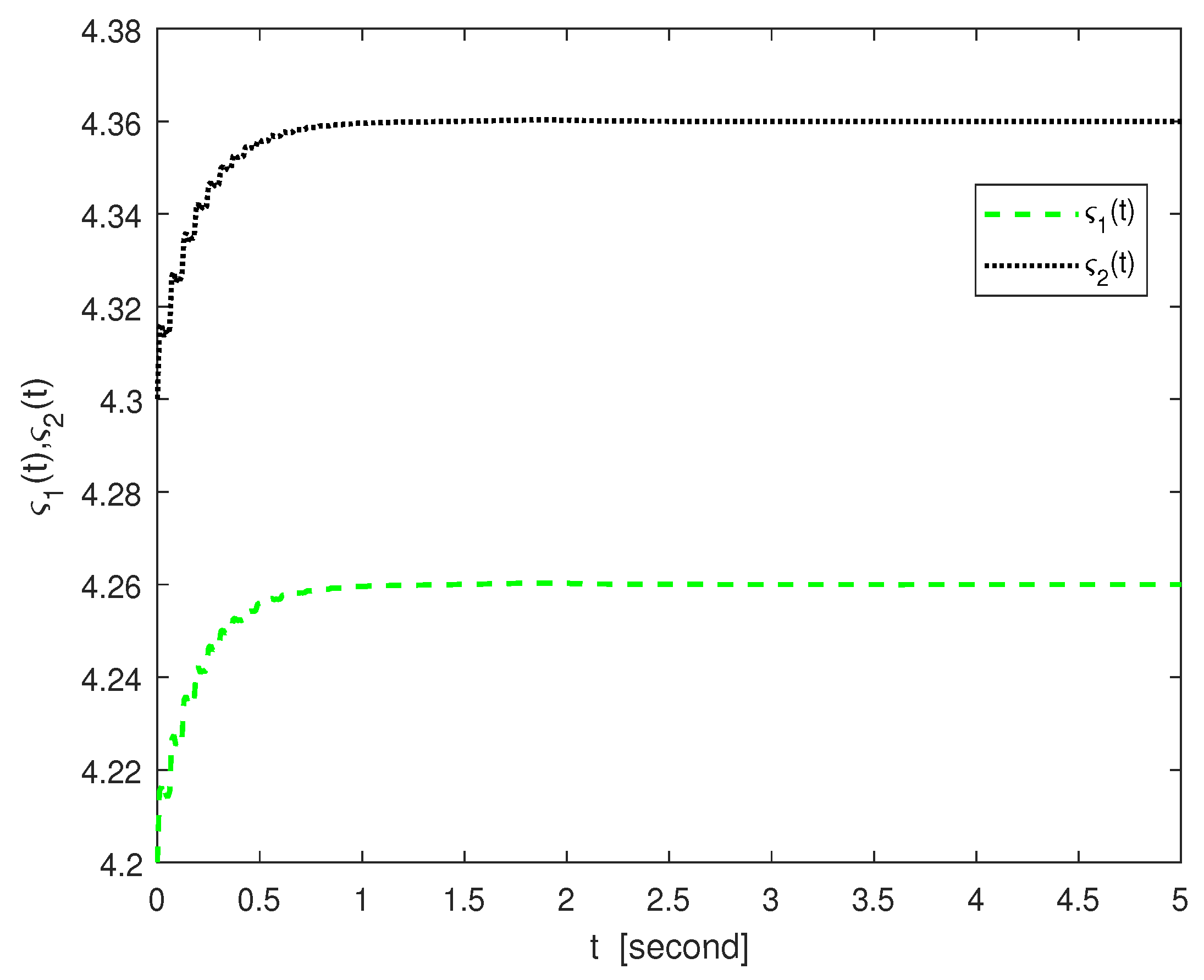
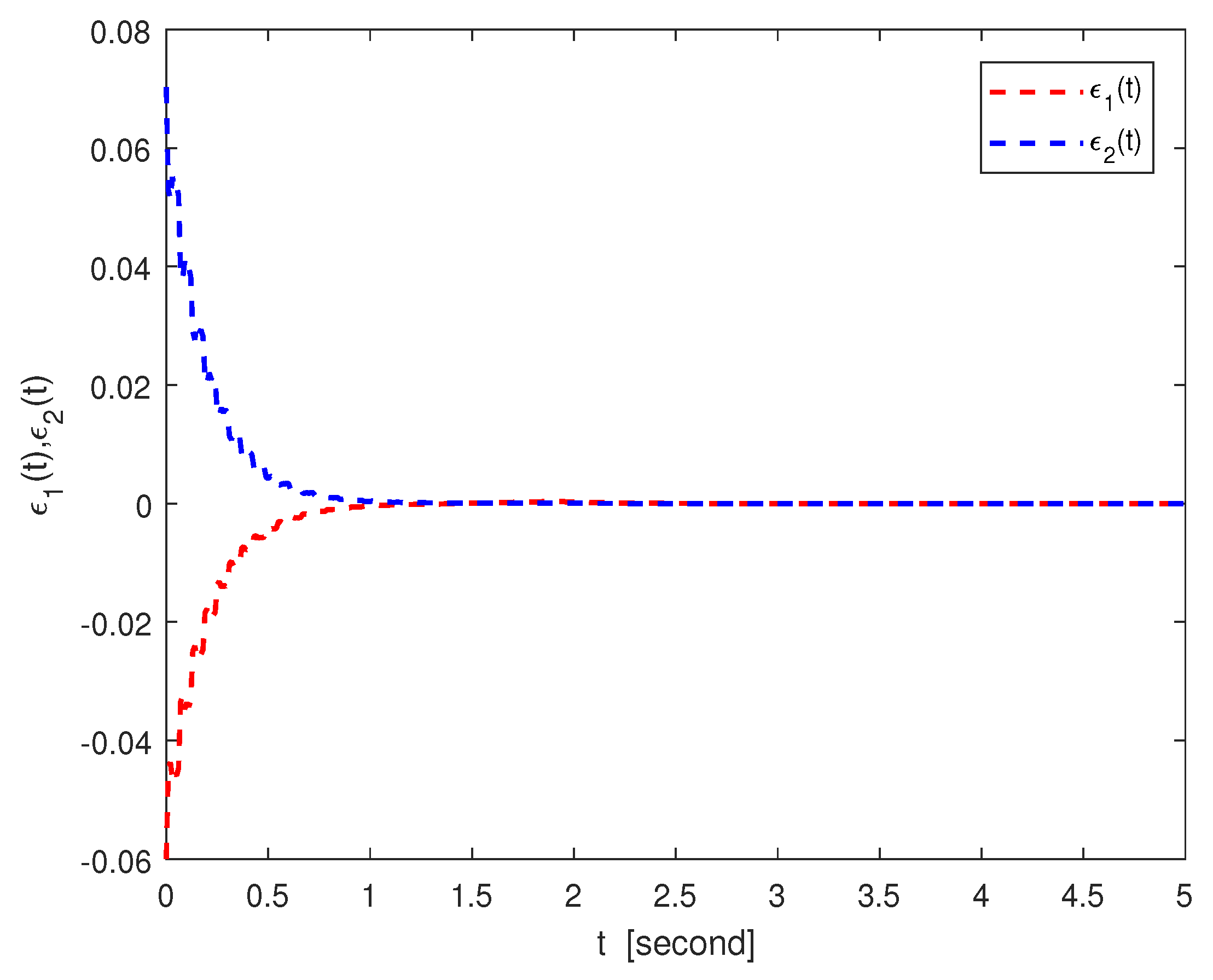
4. Simulation Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, D.; Tang, Z.; Park, J.H.; Ji, Z.C. Quasi-bipartite synchronization of derivatively coupled complex dynamic networks: Memory-based self-triggered approach. IEEE Trans. Syst. Man, Cybern. Syst. 2024, 54, 1611–1621. [Google Scholar] [CrossRef]
- Zhao, C.; Chen, Y.P.; Shi, K.B.; Zhang, L.; Nie, Y.J. A relaxed Lyapunov function lemma and genetic algorithm applying to time-delay systems. Chaos Solitons Fractals 2025, 199, 116687. [Google Scholar] [CrossRef]
- Xiao, J.Y.; Li, Y.T. Deep analysis on MLSY for fractional-order higher-dimension-valued neural networks under the action of free quadratic coefficients. Expert Syst. Appl. 2026, 298, 129586. [Google Scholar] [CrossRef]
- Pham, H.; Warin, X. Mean-field neural networks: Learning mappings on Wasserstein space. Neural Netw. 2023, 168, 380–393. [Google Scholar] [CrossRef] [PubMed]
- Ding, D.; Tang, Z.; Park, J.H.; Wang, Y.; Ji, Z.C. Dynamic self-triggered impulsive synchronization of complex networks with mismatched parameters and distributed delay. IEEE Trans. Cybern. 2023, 53, 887–899. [Google Scholar] [CrossRef]
- Luo, R.F.; Ren, J.J.; Shi, K.B. Stability analysis of delayed T-S fuzzy power system via a cubic function negative determination lemma. Nonlinear Dyn. 2025, 113, 5439–5456. [Google Scholar] [CrossRef]
- Fan, H.G.; Chen, X.J.; Shi, K.B.; Wen, H. Distributed delayed impulsive control for μ-synchronization of multi-link structure networks with bounded uncertainties and time-varying delays of unmeasured bounds: A novel Halanay impulsive inequality approach. Chaos Solitons Fractals 2024, 186, 115226. [Google Scholar] [CrossRef]
- Han, T.Y.; Liang, Y.; Fan, W.J. Dynamics and soliton solutions of the perturbed Schrodinger-Hirota equation with cubic-quintic-septic nonlinearity in dispersive media. Aims Math. 2025, 10, 754–776. [Google Scholar] [CrossRef]
- Zhang, K.; Cao, J.P.; Lyu, J.J. Dynamic behavior and modulation instability for a generalized nonlinear Schrodinger equation with nonlocal nonlinearity. Phys. Scr. 2025, 100, 015262. [Google Scholar] [CrossRef]
- Tang, Z.; Xuan, D.L.; Park, J.H.; Wang, Y.; Feng, J.W. Impulsive effects based distributed synchronization of heterogeneous coupled neural networks. IEEE Trans. Netw. Sci. Eng. 2021, 8, 498–510. [Google Scholar] [CrossRef]
- Cai, J.Y.; Yi, C.B.; Luo, X.; Xiao, C.R. Output feedback tracking consensus of switched stochastic uncertain multiagent systems via event-triggered control. IEEE Syst. J. 2024, 308, 130–141. [Google Scholar] [CrossRef]
- Ding, K.; Zhu, Q.X. A note on sampled-data synchronization of memristor networks subject to actuator failures and two different activations. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2097–2101. [Google Scholar] [CrossRef]
- Yi, C.B.; Cai, J.Y.; Guo, R. Synchronization of a class of nonlinear multiple neural networks with delays via a dynamic event-triggered impulsive control strategy. Electron. Res. Arch. 2024, 32, 4581–4603. [Google Scholar] [CrossRef]
- Yao, W.; Wang, C.H.; Sun, Y.C.; Gong, S.Q.; Lin, H.R. Event-triggered control for robust exponential synchronization of inertial memristive neural networks under parameter disturbance. Neural Netw. 2023, 164, 67–80. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Yang, Y.Q. Quasi-Mittag-Leffler projective synchronization of delayed chaotic fractional order neural network with mismatched parameters. Fractal Fract. 2025, 9, 379. [Google Scholar]
- Fan, H.G.; Shi, K.B.; Guo, Z.Z.; Zhou, A.R. Finite-time synchronization criteria for Caputo fractional-order uncertain memristive neural networks with fuzzy operators and transmission delay under communication feedback. Fractal Fract. 2024, 8, 619. [Google Scholar] [CrossRef]
- Zhao, L.H.; Wen, S.P.; Xu, M.; Shi, K.B.; Zhu, S.; Huang, T.W. PID control for output synchronization of multiple output coupled complex networks. IEEE Trans. Netw. Sci. Eng. 2022, 9, 1553–1566. [Google Scholar] [CrossRef]
- Liu, S.R.; Liu, X.W. Output synchronization and PID control for directed networks with multiple communications. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 1620–1633. [Google Scholar]
- Suid, M.H.; Ahmad, M.A. Optimal tuning of sigmoid PID controller using Nonlinear Sine Cosine Algorithm for the Automatic Voltage Regulator system. ISA Trans. 2022, 128, 265–286. [Google Scholar] [CrossRef]
- Ghazali, M.R.; Ahmad, M.A.; Ismail, R.M.T.R. A multiple-node hormone regulation of neuroendocrine-PID (MnHR-NEPID) control for nonlinear MIMO systems. IETE J. Res. 2022, 68, 4476–4491. [Google Scholar] [CrossRef]
- Li, L. A novel optimization control of gas turbine based on a hybrid method using the BELBIC and adaptive multi input multi output feedback control. J. Intell. Fuzzy Syst. 2023, 45, 863–876. [Google Scholar] [CrossRef]
- Huan, M.C.; Li, C.D. Synchronization of reaction-diffusion neural networks with sampled-data control via a new two-sided looped-functional. Chaos Solitons Fractals 2023, 167, 113059. [Google Scholar] [CrossRef]
- Cui, Y.; Ge, X.H.; Cheng, P.; Liu, X. Resilient synchronization of interconnected dynamical networks with DoS attacks: An adaptive event-triggered control approach. Neurocomputing 2025, 638, 130192. [Google Scholar] [CrossRef]
- Fan, H.G.; Rao, Y.; Shi, K.B.; Wen, H. Time-varying function matrix projection synchronization of Caputo fractional-order uncertain memristive neural networks with multiple delays via mixed open loop feedback control and impulsive control. Fractal Fract. 2024, 8, 301. [Google Scholar] [CrossRef]
- Alsaedi, A.; Cao, J.D.; Ahmad, B.; Alshehri, A.; Tan, X.G. Synchronization of master-slave memristive neural networks via fuzzy output-based adaptive strategy. Chaos Solitons Fractals 2022, 158, 112095. [Google Scholar] [CrossRef]
- Liu, F.; Song, Q.; Wen, G.H.; Cao, J.D.; Yang, X.S. Bipartite synchronization in coupled delayed neural networks under pinning control. Neural Netw. 2018, 108, 146–154. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Li, C.D.; Li, H.F.; Cao, Z.R. Synchronization of uncertain coupled neural networks with time-varying delay of unknown bound via distributed delayed impulsive control. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 3624–3635. [Google Scholar] [CrossRef]
- Hua, W.T.; Wang, Y.T.; Liu, C.Y. New method for global exponential synchronization of multi-link memristive neural networks with three kinds of time-varying delays. Appl. Math. Comput. 2024, 471, 128593. [Google Scholar] [CrossRef]
- Wan, P.; Zhou, Y.F.; Zeng, Z.G. Adaptive drive-response synchronization of timescale-type neural networks with unbounded time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 1056–1068. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Wei, X.F.; Wang, S.Z.; Lin, C.; Chen, J. Fixed-time pinning common synchronization and adaptive synchronization for delayed quaternion-valued neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 2276–2289. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Chen, B.S.; Chen, J.J. Global asymptotical ω-periodicity of a fractional-order non-autonomous neural networks. Neural Netw. 2015, 68, 78–88. [Google Scholar] [CrossRef]
- Bhalekar, S.; Gejji, V. A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order. J. Fract. Calc. Appl. 2011, 1, 1–9. [Google Scholar]
- Duan, L.; Wei, H.; Huang, L.H. Finite-time synchronization of delayed fuzzy cellular neural networks with discontinuous activations. Fuzzy Sets and Systems 2019, 361, 56–70. [Google Scholar] [CrossRef]
- Yang, X.J.; Li, C.D.; Song, Q.K.; Chen, J.Y.; Huang, J.J. Global Mittag-Leffler stability and synchronization analysis of fractional-order quaternion-valued neural networks with linear threshold neurons. Neural Networks 2018, 105, 88–103. [Google Scholar] [CrossRef] [PubMed]
- Peng, Q.; Lin, S.M.; Tan, M.C. Quantized hybrid impulsive control for finite-time synchronization of fractional-order uncertain multiplex networks with multiple time-varying delays. Commun. Nonlinear Sci. Numer. Simul. 2025, 142, 108540. [Google Scholar] [CrossRef]
- Pan, H.H.; Huang, C.D.; Cao, J.D.; Liu, H. Global Mittag-Leffler synchronization of discontinuous memristor-based fractional-order fuzzy inertial neural networks with mixed delays. Neurocomputing 2025, 626, 129475. [Google Scholar] [CrossRef]
- Xiao, J.Y.; Zhong, S.M.; Li, Y.T.; Xu, F. Finite-time Mittag-Leffler synchronization of fractional-order memristive BAM neural networks with time delays. Neurocomputing 2017, 219, 431–439. [Google Scholar] [CrossRef]
- Popa, C.A.; Kaslik, E. Finite-time Mittag-Leffler synchronization of neutral-type fractional-order neural networks with leakage delay and time-varying delays. Mathematics 2020, 8, 1146. [Google Scholar] [CrossRef]
- Xiao, J.Y.; Cao, J.D.; Cheng, J.; Zhong, S.M.; Wen, S.P. Novel methods to finite-time Mittag-Leffler synchronization problem of fractional-order quaternion-valued neural networks. Inf. Sci. 2020, 526, 221–244. [Google Scholar] [CrossRef]
- Du, F.F.; Lu, J.G. Adaptive finite-time synchronization of fractional-order delayed fuzzy cellular neural networks. Fuzzy Sets Syst. 2023, 466, 108480. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, Z.; Li, W.X.; Wu, Y.B. Exponential stability of fractional-order fuzzy multilayer networks with short memory and noninstantaneous impulses via intermittent control. IEEE Trans. Fuzzy Syst. 2025, 33, 1639–1649. [Google Scholar] [CrossRef]
- Su, Y.; Hu, C.; Yu, J.; Wen, S.P.; Li, H.L. Bipartite output synchronization of fuzzy fractional output-coupled networks via membership function-dependent adaptive control. IEEE Trans. Autom. Sci. Eng. 2025, 22, 14147–14157. [Google Scholar]
- Zhang, H.M.; Yin, X.N.; Zhang, H.; Zhang, W.W. Global Mittag-Leffler lag projective synchronization for Caputo-type delayed Cohen-Grossberg fuzzy neural networks. Int. J. Control Autom. Syst. 2025, 23, 212–222. [Google Scholar] [CrossRef]
- Li, R.X.; Cao, J.D. Stabilization and synchronization control of quaternion-valued fuzzy memristive neural networks: Nonlinear scalarization approach. Fuzzy Sets Syst. 2024, 477, 108832. [Google Scholar] [CrossRef]
- Li, H.L.; Cao, J.D.; Hu, C.; Zhang, L.; Jiang, H.J. Adaptive control-based synchronization of discrete-time fractional-order fuzzy neural networks with time-varying delays. Neural Netw. 2023, 168, 59–73. [Google Scholar] [CrossRef] [PubMed]
- Li, H.L.; Cao, J.D.; Hu, C.; Jiang, H.J.; Alsaedi, A. Synchronization analysis of nabla fractional-order fuzzy neural networks with time delays via nonlinear feedback control. Fuzzy Sets Syst. 2024, 475, 108750. [Google Scholar] [CrossRef]
- Zhao, F.; Jian, J.G.; Wang, B.X. Finite-time synchronization of fractional-order delayed memristive fuzzy neural networks. Fuzzy Sets Syst. 2023, 467, 108578. [Google Scholar] [CrossRef]
- Ansari, M.S.H.; Malik, M. Projective synchronization of fractional order quaternion valued uncertain neural networks. Chin. J. Phys. 2024, 88, 740–755. [Google Scholar] [CrossRef]
- Chen, R.; Li, H.L.; Liu, H.; Jiang, H.J.; Cao, J.D. Complete synchronization of discrete-time fractional-order T-S fuzzy complex-valued neural networks with time delays and uncertainties. IEEE Trans. Fuzzy Syst. 2025, 33, 842–856. [Google Scholar] [CrossRef]
- Du, F.F.; Luo, J.G. Finite-time synchronization of fractional-order delayed fuzzy cellar neural networks with parameter uncertainties. IEEE Trans. Fuzzy Syst. 2023, 31, 1769–1779. [Google Scholar] [CrossRef]
- Fan, H.G.; Chen, X.J.; Shi, K.B.; Liang, Y.H.; Wang, Y.; Wen, H. Mittag-Leffler synchronization in finite time for uncertain fractional-order multi-delayed memristive neural networks with time-varying perturbations via information feedback. Fractal Fract. 2024, 8, 422. [Google Scholar] [CrossRef]
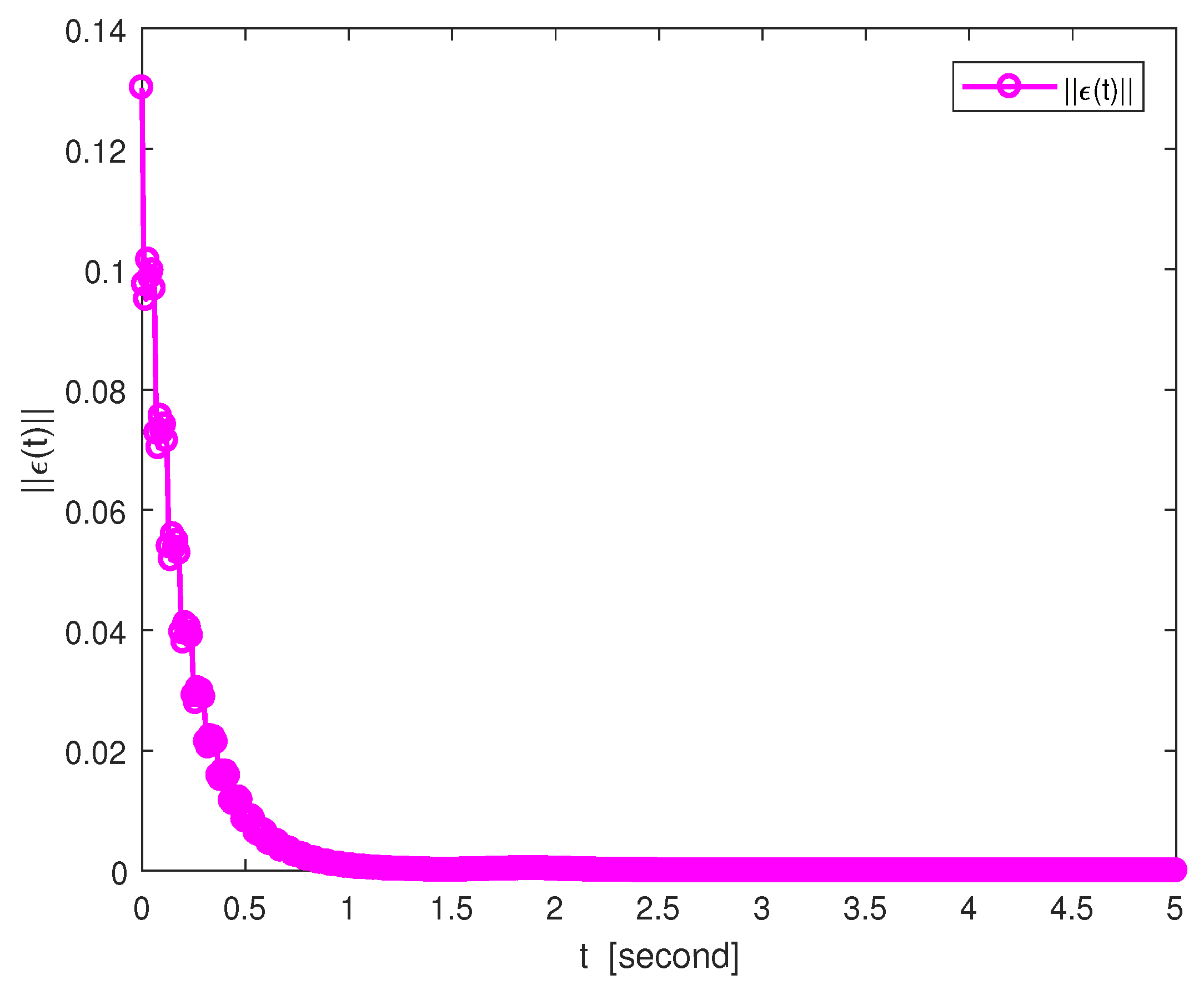
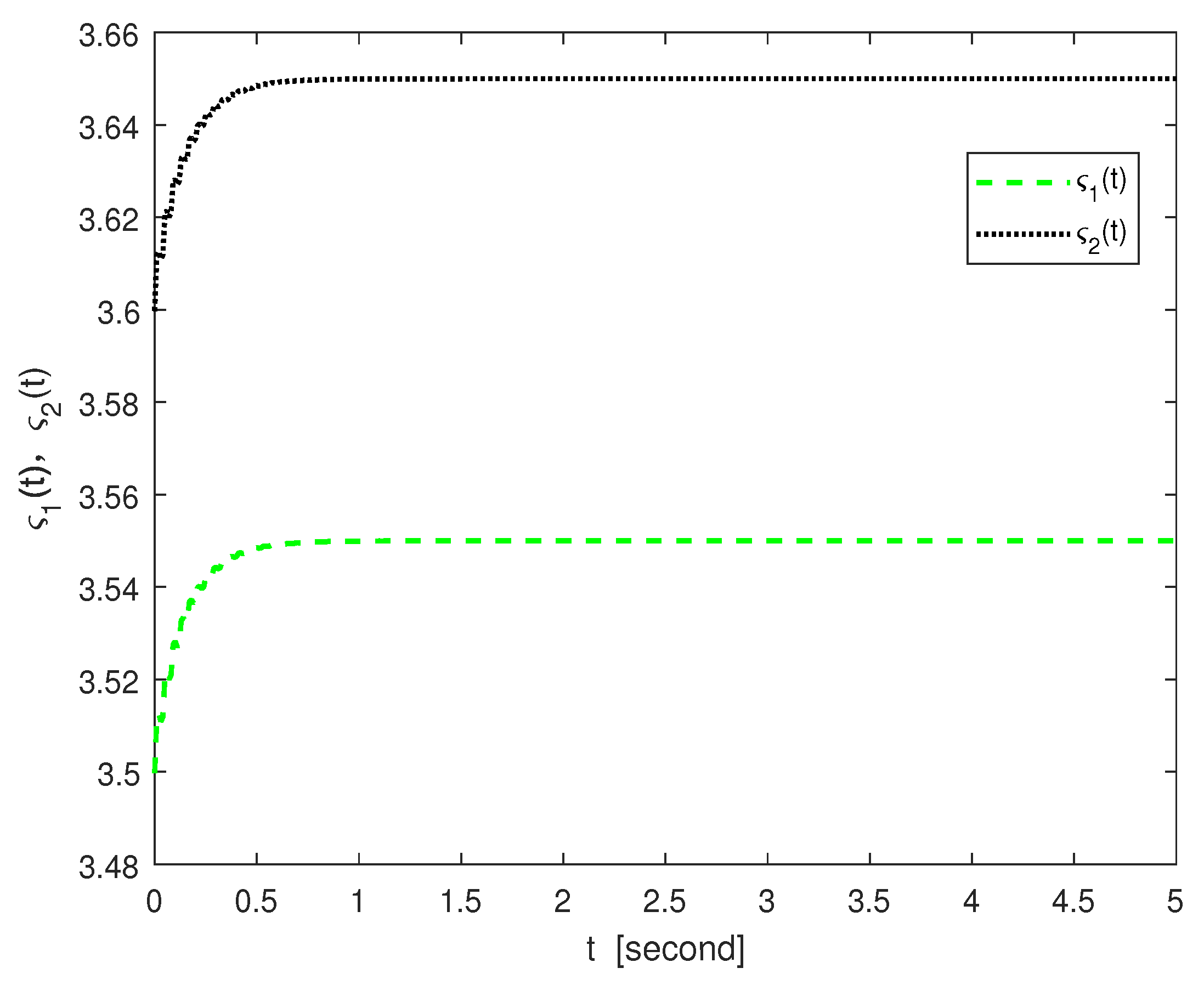
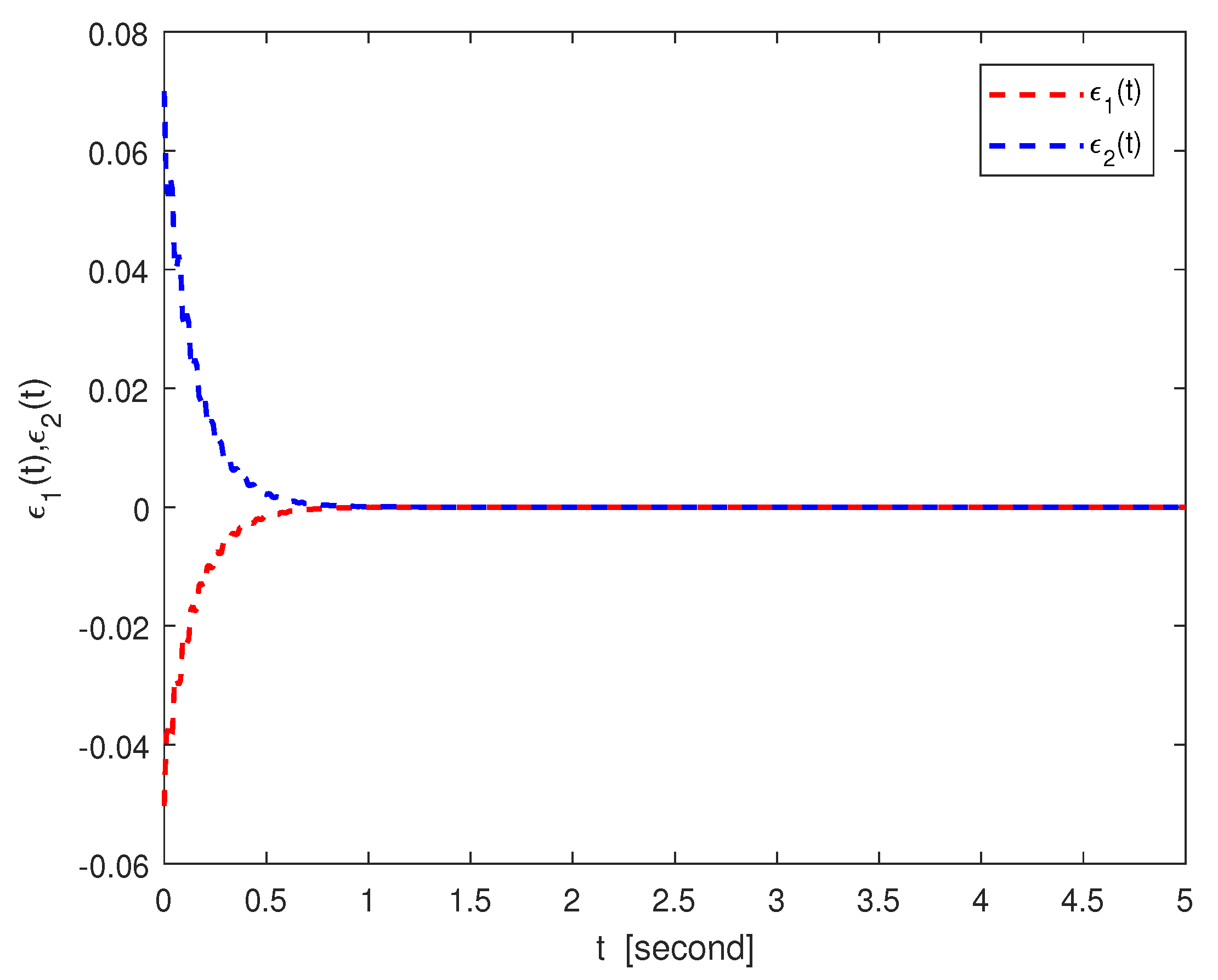

| Time t | 0.1 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 |
|---|---|---|---|---|---|---|---|
| Error norm | 0.0793 | 0.0418 | 0.0186 | 0.0052 | 0.0025 | 0.0010 | 0 |
| 0.15 sint | 0.20 sint | 0.25 sint | 0.30 sint | 0.35 sint | 0.40 sint | |
|---|---|---|---|---|---|---|
| Mean time | 1.246 | 1.424 | 1.713 | 2.178 | 2.559 | 2.959 |
| Variance | 0.023 | 0.024 | 0.028 | 0.028 | 0.029 | 0.032 |
| Delays | 0.05 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
|---|---|---|---|---|---|---|
| Mean time | 0.236 | 0.616 | 0.827 | 1.153 | 1.962 | 3.248 |
| Variance | 0.012 | 0.013 | 0.014 | 0.022 | 0.026 | 0.031 |
| Strengths | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 |
|---|---|---|---|---|---|---|
| Mean time | 1.152 | 0.993 | 0.784 | 0.635 | 0.493 | 0.346 |
| Variance | 0.021 | 0.019 | 0.018 | 0.018 | 0.017 | 0.016 |
| Strengths | 4.8 | 4.9 | 5.0 | 5.1 | 5.2 | 5.3 |
|---|---|---|---|---|---|---|
| Mean time | 1.143 | 1.092 | 1.014 | 0.957 | 0.865 | 0.732 |
| Variance | 0.020 | 0.019 | 0.019 | 0.018 | 0.018 | 0.017 |
| Time t | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
|---|---|---|---|---|---|---|---|
| Error norm | 0.0372 | 0.0243 | 0.0068 | 0.0037 | 0.0018 | 0.0005 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, H.; Shi, K.; Guo, Z.; Zhou, A.; Cai, J. Finite-Time Synchronization and Mittag–Leffler Synchronization for Uncertain Fractional-Order Delayed Cellular Neural Networks with Fuzzy Operators via Nonlinear Adaptive Control. Fractal Fract. 2025, 9, 634. https://doi.org/10.3390/fractalfract9100634
Fan H, Shi K, Guo Z, Zhou A, Cai J. Finite-Time Synchronization and Mittag–Leffler Synchronization for Uncertain Fractional-Order Delayed Cellular Neural Networks with Fuzzy Operators via Nonlinear Adaptive Control. Fractal and Fractional. 2025; 9(10):634. https://doi.org/10.3390/fractalfract9100634
Chicago/Turabian StyleFan, Hongguang, Kaibo Shi, Zizhao Guo, Anran Zhou, and Jiayi Cai. 2025. "Finite-Time Synchronization and Mittag–Leffler Synchronization for Uncertain Fractional-Order Delayed Cellular Neural Networks with Fuzzy Operators via Nonlinear Adaptive Control" Fractal and Fractional 9, no. 10: 634. https://doi.org/10.3390/fractalfract9100634
APA StyleFan, H., Shi, K., Guo, Z., Zhou, A., & Cai, J. (2025). Finite-Time Synchronization and Mittag–Leffler Synchronization for Uncertain Fractional-Order Delayed Cellular Neural Networks with Fuzzy Operators via Nonlinear Adaptive Control. Fractal and Fractional, 9(10), 634. https://doi.org/10.3390/fractalfract9100634








