Dynamics of Complex Systems and Their Associated Attractors in a Multifractal Paradigm of Motion

Abstract

In this paper we analyze complex systems dynamics using a multifractal framework derived from Scale Relativity Theory (SRT). By extending classical differential geometry to accommodate non-differentiable, scale-dependent behaviors, we formulate Schrödinger-type equations that describe multifractal geodesics. These equations reveal deep analogies between quantum mechanics and macroscopic complex dynamics. A key feature of this approach is the identification of hidden symmetries governed by multifractal analogs of classical groups, particularly the SL(2ℝ) group. These symmetries help explain universal dynamic behaviors such as double period dynamics, damped dynamics, modulated dynamics, or chaotic dynamics. The resulting framework offers a unified geometric and algebraic perspective on the emergence of order within complex systems, highlighting the fundamental role of fractality and scale covariance in nature.

1. Introduction

A defining characteristic of complex systems across all scientific domains—from the turbulent eddies in a fluid flow to the intricate networks of cardiac regulation and the large-scale structure of the cosmos—is the manifestation of structure and dynamics across a vast hierarchy of scales [1]. The branching patterns of the vascular system, for instance, exhibit a self-similar architecture that spans from major arteries down to microscopic capillaries [2]. Similarly, the temporal fluctuations of a healthy heartbeat display a fractal complexity that is statistically self-similar over multiple orders of magnitude in time [3]. This ubiquity of scale-dependent phenomena presents a profound challenge to traditional physical descriptions. Classical mechanics and general relativity, founded upon the mathematics of smooth, differentiable manifolds, provide powerful predictive frameworks at specific, well-defined scales but often struggle to offer a unified description that remains consistent and coherent across this entire hierarchy. The core problem lies in the assumption of differentiability itself, which implicitly presupposes a world that becomes smooth and simple at sufficiently small scales, a notion that is increasingly challenged by empirical observations of natural complexity.

The study of complex systems was revolutionized by the development of nonlinear dynamics and chaos theory. These frameworks provided, for the first time, a deterministic explanation for seemingly random and unpredictable behavior in a wide array of systems and applications [4]. The central discovery was that simple, deterministic nonlinear equations could generate extraordinarily complex dynamics, characterized by a sensitive dependence on initial conditions—commonly known as the “butterfly effect” [5]. This sensitivity renders long-term prediction impossible, as even infinitesimal uncertainties in the initial state grow exponentially over time [6].

A signal achievement of chaos theory was the recognition that the long-term evolution of these dissipative systems often converges onto geometric objects in phase space known as strange attractors. These attractors were found to possess a fractal structure, meaning they exhibit intricate, self-similar detail at arbitrarily small scales [7]. The mathematics of chaos theory, supported by a highly evolved language of stability theory and bifurcation analysis, has provided a sophisticated toolbox for describing and classifying these behaviors [8].

However, a crucial distinction must be made. While chaos theory and nonlinear dynamics are exceptionally powerful at describing how fractal structures emerge from the evolution of deterministic equations, they do not typically address the more fundamental question of why the underlying fabric of a system’s dynamics should be fractal in the first place. Fractality in this context is an emergent property, a result of the system’s evolution, rather than a foundational postulate about the nature of the space in which that evolution occurs. This distinction highlights a conceptual gap: these theories describe the properties of complexity without necessarily providing an ab initio geometric principle for its origin.

A parallel development in theoretical physics that directly engaged with the problem of scale was the formulation of the renormalization group (RG). Originating in quantum field theory and statistical mechanics, the RG is a formal mathematical apparatus for systematically investigating how the description of a physical system changes as it is viewed at different length or energy scales [9]. The core idea involves a “coarse-graining” or “blocking” procedure, where microscopic degrees of freedom are integrated out to yield an effective theory at a larger scale [10]. This process reveals how the parameters of the theory, such as coupling constants and masses, “flow” as the scale changes. The fixed points of this flow correspond to scale-invariant theories and explain the phenomenon of universality, where disparate microscopic systems exhibit identical behavior near critical points (e.g., phase transitions) [10].

The RG represents a monumental step towards a physics of scale. However, Laurent Nottale, the originator of Scale Relativity Theory, has pointed out that the standard RG framework can be viewed as a “Galilean version of scale relativity” [11,12,13]. This analogy is deeply insightful. In the relativity of motion, Galilean transformations are a low-velocity approximation to the more fundamental Lorentz transformations of special relativity. The latter are required when velocities approach an invariant, impassable speed—the speed of light. Nottale argues that the transformations of the RG are analogous to a Galilean group of scale transformations, which are valid in many regimes. Scale Relativity Theory (SRT) proposes to complete this picture by introducing a “Lorentzian” structure to the relativity of scales. In this new framework, the Planck scale is postulated to play the role of a minimal, impassable length scale, which is invariant under scale transformations (dilations), just as the speed of light is invariant under motion transformations (boosts) [11,12,13]. This positions SRT not as a competitor to the RG, but as its logical, relativistic generalization, one that should recover RG-like behavior in certain limits while also providing new physical insights where the full “Lorentzian” scale structure becomes significant.

This work is grounded in the framework of Scale Relativity Theory (SRT), first proposed by Nottale [11,12,13]. The theory’s foundational premise is a radical extension of Einstein’s principle of relativity. While Einstein’s theories established the relativity of position, orientation, and motion, SRT postulates that the laws of physics must also be covariant with respect to the scale of observation. In this view, resolution is not merely a feature of a measurement apparatus but a fundamental characteristic of the coordinate system itself, a “state of scale” that must be explicitly included in the physical description [11,12,13].

The most profound consequence of this postulate is the necessary abandonment of the assumption of spacetime differentiability. A physical quantity that depends explicitly on scale cannot be described by a smooth, differentiable function. If spacetime coordinates themselves are subject to the principle of scale relativity, then the geometry of spacetime must be continuous but fundamentally non-differentiable. Such a geometry is, by its nature, fractal. Therefore, in SRT, fractality is not an emergent property of dynamics but a foundational property of spacetime itself. The complex, non-differentiable trajectories of particles are understood as geodesics within this fractal spacetime.

The objective of this paper is to develop the consequences of this scale-relativistic postulate for the dynamics of complex systems. We will first elaborate on the mathematical formalism of motion in a multifractal space, clarifying key derivations and justifying underlying assumptions. We will then show how this formalism leads to the emergence of Schrödinger-type equations and reveals hidden symmetries, governed by the SL(2ℝ) group, that act as synchronization modes.

2. Key Aspects of the Scale Relativity Theory

In what follows, we admit that the motions of the structural units of any complex system are described by continuous and non-differentiable curves (multifractal curves). This departure from classical mechanics has several immediate and significant consequences [13,14]:

First, any such curve is explicitly dependent on the resolution scale, denoted $\delta t$. According to the Lebesgue theorem, the length of a non-differentiable curve tends to infinity as the measurement interval $\delta t$ tends to zero. This scale-divergent behavior is the defining characteristic of a fractal curve. Consequently, the space in which the system’s dynamics unfold is itself a fractal in the sense of Mandelbrot [15].

Second, the dynamics of any complex system are related to the behavior of a set of functions during the zoom operation of $\delta t$, i.e., $\delta t\equiv dt$ through the functionality of the substitution principle.

The dynamics of any complex system are described through multifractal variables. Then, two derivatives of any variable field $Q\left(t,dt\right)$ which describes the complex system dynamics, can be defined:

$$\begin{gathered} {\left({\displaystyle \frac{dQ}{dt}}\right)}_{+}=\underset{\Delta t\to 0}{\mathit{lim}}{\displaystyle \frac{Q\left(t,t+\Delta t\right)-Q\left(t,\Delta t\right)}{\Delta t}} \\ {\left({\displaystyle \frac{dQ}{dt}}\right)}_{-}=\underset{\Delta t\to 0}{\mathit{lim}}{\displaystyle \frac{Q\left(t,\Delta t\right)-Q\left(t-\Delta t,\Delta t\right)}{\Delta t}} \end{gathered}$$

(1)

The sign “$+$” corresponds to the forward dynamics, while the sign “$-$” corresponds to the backward ones.

The differential of the spatial coordinate field has the form:

$$d_{\pm }{X}^i\left(t,dt\right)=d_{\pm }{x}^i\left(t\right)+d_{\pm }\xi \left(t,dt\right)$$

(2)

The differentiable part of $X^i$, i.e., $d_{\pm }{x}^i\left(t\right)$ is scale resolution independent. The non-differentiable part of $X^i$, i.e., $d_{\pm }\xi \left(t,dt\right)$ is scale resolution dependent.

The non-differentiable part of the spatial coordinate field, which describes the complex system dynamics, satisfies the non-differentiable multifractal equation [15,16,17]

$$d_{\pm }{\xi }^i\left(t,dt\right)={{\lambda }_{\pm }^i\left(dt\right)}^{\left[{\displaystyle \frac{2}{f\left(\alpha \right)}}\right]-1}$$

(3)

where ${\lambda }_{\pm }^i$ are constant coefficients related to the differentiable–non-differentiable scale transition, $f\left(\alpha \right)$ is the singularity spectrum of order $\alpha$, of fractal dimension $D_F$, and $\alpha$ is the singularity index. One can find various definitions for fractal dimensions, like the ones given by Kolmogorov, or Hausdorff-Besikovich, etc. [15]. When employing one of these definitions in complex system dynamics, it is essential that the fractal dimension remains constant and arbitrary during the whole analysis. Usually, $D_F<2$ can be chosen for correlative processes, while $D_F>2$ is used for non–correlative processes [13]. In such a conjecture, through (3), it is possible to identify not only the “areas” of the complex system dynamics that are characterized by a certain fractal dimension (i.e., in the case of monofractal dimensions), but also the number of “areas” in which fractal dimensions are situated in a values interval (i.e., in the case of multifractal dimensions). Furthermore, the singularity spectrum $f\left(\alpha \right)$ enables the identification of universality classes within the dynamics of complex systems, even when regular or strange attractors exhibit distinct characteristics [15,17].

To recover time-reflection invariance at a formal level, we introduce a complex operator that combines these two derivatives. This outcome is a logical consequence of Cresson’s Theorem, which establishes a solid basis for this scale calculus [18]. The complex time derivative operator is defined as follows:

$${\displaystyle \frac{\widehat{d}}{dt}}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{d_{+}+d_{-}}{dt}}\right)-{\displaystyle \frac{i}{2}}\left({\displaystyle \frac{d_{+}-d_{-}}{dt}}\right)$$

(4)

Applying this operator to the spatial coordinate field $X^i$, yields a complex velocity field:

$${\widehat{V}}^i={\displaystyle \frac{\widehat{d}{X}^i}{dt}}=V_D^i-V_F^i$$

(5)

This complex velocity elegantly separates the dynamics into two distinct components:

$$\begin{gathered} V_D^i={\displaystyle \frac{1}{2}}{d}_{+}{X}^i+{\displaystyle \frac{d_{+}{X}^i}{dt}}, \\ {V}_F^i={\displaystyle \frac{1}{2}}{d}_{+}{X}^i-{\displaystyle \frac{d_{-}{X}^i}{dt}}, \\ i=1,2,3 \end{gathered}$$

(6)

The real part of ${\widehat{V}}^i$, i.e., $V_D^i$ (differential velocity) is scale resolution independent. The imaginary one $V_F^i$ (non–differentiable velocity) is scale resolution dependent. This separation is a powerful feature of the formalism, as it ensures that classical dynamics are recovered as the scale-independent, real component of the full complex dynamic.

Since the multifractalization describing complex system dynamics implies stochasticization [15,16,17], the whole statistic “arsenal” in the form of averages, variances, covariances, etc., becomes operational. Thus, let us choose for the average of $d_{\pm }{X}^i$ the following functionality:

$$⟨d_{\pm }{X}^i⟩\equiv d_{\pm }{x}^i$$

(7)

with

$$⟨d_{\pm }{\xi }^i⟩=0$$

(8)

Equation (8) implies that the average of the non-differential part of the spatial coordinate field is null.

A scale covariant derivative can be employed to describe complex system dynamics. This scale covariant derivative is given by the operator [14,19]:

$${\displaystyle \frac{\widehat{d}}{dt}}={\partial }_t+{\widehat{V}}^i{\partial }_i+{\displaystyle \frac{1}{4}}{\left(dt\right)}^{\left[{\displaystyle \frac{2}{f\left(\alpha \right)}}\right]-1}{D}^{lk}{\partial }_l{\partial }_k$$

(9)

where

$$D^{lk}{\partial }_l=\left({\lambda }_{+}^l{\lambda }_{+}^k-{\lambda }_{-}^l{\lambda }_{-}^k\right)+i\left({\lambda }_{+}^l{\lambda }_{+}^k+{\lambda }_{-}^l{\lambda }_{-}^k\right), {\partial }_t={\displaystyle \frac{\partial }{\partial t}}, {\partial }_i={\displaystyle \frac{\partial }{\partial X^i}}, {\partial }_l{\partial }_k={\displaystyle \frac{{\partial }^2}{\partial X^l\partial X^k}}$$

(10)

The third term from Equation (9), ${\left(dt\right)}^{\left[{\displaystyle \frac{2}{f\left(\alpha \right)}}\right]-1}{D}^{lk}{\partial }_l{\partial }_k$, is the novel contribution arising directly from the non-differentiable, multifractal nature of spacetime. It is a diffusion-like term, where the “diffusion” is not due to random molecular collisions in the classical sense, but is an intrinsic consequence of the fractal geometry. The coefficient of this term explicitly depends on the time resolution dt and the multifractal singularity spectrum $f\left(\alpha \right)$, highlighting the scale-dependent nature of these dynamics. The tensor $D^{lk}$ captures the anisotropies of this fractal diffusion process.

The general form of the scale covariant derivative in Equation (9) is complex. To proceed with deriving a tractable equation of motion, we introduce a simplifying assumption about the nature of the underlying stochastic process that is induced by multifractalization. Specifically, we consider the case of Markov-type stochastic processes [20].

A Markov process is one that is “memoryless,” meaning its future state depends only on its present state, not on the sequence of events that preceded it [21]. While many complex systems in nature do exhibit long-range memory, a hallmark of non-Markovian behavior, the Markovian assumption is a powerful and widely used approximation in modeling complex systems. It is particularly valid for systems where the influence of past states decays sufficiently rapidly, such that on the timescale of interest, the dynamics are dominated by the current state. This assumption makes the problem analytically tractable by significantly simplifying the mathematical structure [22]. We acknowledge that non-Markovian effects are significant in many real-world systems, and their inclusion represents an important avenue for future extensions of this model. However, the Markovian case provides a foundational framework from which the core principles of the theory can be elucidated.

In this context, for Markov-type stochastic processes [14,19]), i.e.,

$${\lambda }_{+}^i{\lambda }_{+}^l={\lambda }_{-}^i{\lambda }_{-}^l=2\lambda {\delta }^{il}$$

(11)

and

$$f\left(\alpha \right)\equiv D_F$$

(12)

where $\lambda$ is a specific coefficient associated with the multifractal–non-multifractal scale transition and ${\delta }^{il}$ is Kronecker’s pseudo-tensor, the scale covariant derivative becomes:

$${\displaystyle \frac{\widehat{d}}{dt}}={\partial }_t+{\widehat{V}}^l{\partial }_l-i\lambda {\left(dt\right)}^{\left[{\displaystyle \frac{2}{D_F}}\right]-1}{\partial }_l{\partial }^l$$

(13)

A particularly important case arises when the fractal dimension $D_F=2$. This corresponds to the dynamics of “Peano-type curves.” A Peano curve is a specific type of fractal curve known as a space-filling curve; it is a continuous function that maps a one-dimensional interval onto a two-dimensional square [23,24]. Such a curve is so convoluted and irregular that its fractal dimension is equal to the topological dimension of the space it fills, i.e., $D_F=2.$ In this special case, the scale covariant derivative (13) takes the standard form from the SRT:

$${\displaystyle \frac{\widehat{d}}{dt}}={\partial }_t+{{\widehat{V}}^i}^l{\partial }_l-iD{\partial }_l{\partial }^l$$

(14)

where $\lambda \equiv D$ is the diffusion coefficient associated with the fractal–non–fractal scale transition. Therefore, this model generalizes all the results of Nottale’s theory (i.e., Scale Relativity Theory) [11,12,13]. Moreover, for Compton scale resolution, (14) becomes the quantum operator [11,12,13].

3. Dynamics in Complex Systems Through Schrödinger-Type Regimes at Various Scale Resolutions

Now, accepting the functionality of the scale covariance principle [11,12,13], i.e., applying the operator (9) to the complex velocity fields (5), in the absence of any external constraint, the motion equation (geodesics equation) takes the following form:

$${\displaystyle \frac{{\widehat{d}\widehat{V}}^i}{dt}}={\partial }_t{\widehat{V}}^i+{\widehat{V}}^l{\partial }_l{\widehat{V}}^i+{\displaystyle \frac{1}{4}}{\left(dt\right)}^{\left[{\displaystyle \frac{2}{f\left(\alpha \right)}}\right]-1}{D}^{lk}{\partial }_l{\partial }_k{\widehat{V}}^i=0$$

(15)

This means that for any complex system dynamics, the multifractal acceleration, ${\partial }_t{\widehat{V}}^i$, the multifractal convection, ${\widehat{V}}^l{\partial }_l{\widehat{V}}^i$ and the multifractal dissipation $D^{lk}{\partial }_l{\partial }_k{\widehat{V}}^i$ make their balance in any point of the multifractal curve. Particularly, for (11) and (12), the motion equation (geodesics equation) (15) becomes

$${\displaystyle \frac{{\widehat{d}\widehat{V}}^i}{dt}}={\partial }_t{\widehat{V}}^i+{\widehat{V}}^l{\partial }_l{\widehat{V}}^i-i\lambda {\left(dt\right)}^{\left[{\displaystyle \frac{2}{D_F}}\right]-1}{\partial }_l{\partial }^l{\widehat{V}}^i=0$$

(16)

In what follows, we will separating the complex system dynamics on differentiable and non–differentiable scale resolutions. Thus, Equation (15) becomes

$$\begin{gathered} {\partial }_t{V}_D^i+V_D^l{\partial }_l{V}_D^i-V_F^l{\partial }_l{V}_F^i+{\displaystyle \frac{1}{4}}{\left(dt\right)}^{\left[{\displaystyle \frac{2}{f\left(\alpha \right)}}\right]-1}{D}^{lk}{\partial }_l{\partial }_k{V}_D^i=0 \\ {\partial }_t{V}_F^i+V_F^l{\partial }_l{V}_D^i+V_D^l{\partial }_l{V}_F^i+{\displaystyle \frac{1}{4}}{\left(dt\right)}^{\left[{\displaystyle \frac{2}{f\left(\alpha \right)}}\right]-1}{D}^{lk}{\partial }_l{\partial }_k{V}_F^i=0, \end{gathered}$$

(17)

while (16) takes the form:

$$\begin{gathered} {\partial }_t{V}_D^i+V_D^l{\partial }_l{V}_D^i-\left[V_F^l+\lambda {\left(dt\right)}^{\left[{\displaystyle \frac{2}{f\left(\alpha \right)}}\right]-1}{\partial }^l\right]{\partial }_l{V}_F^i=0 \\ {\partial }_t{V}_F^i+V_D^l{\partial }_l{V}_F^i+\left[V_F^l+\lambda {\left(dt\right)}^{\left[{\displaystyle \frac{2}{f\left(\alpha \right)}}\right]-1}{\partial }^l\right]{\partial }_l{V}_D^i=0. \end{gathered}$$

(18)

For irrotational motions of the complex system dynamics, the complex velocity fields (5) become

$${\widehat{V}}^i=-2i\lambda (dt{)}^{\left[{\displaystyle \frac{2}{f\left(\alpha \right)}}\right]-1}{\partial }^i\mathit{ln}\Psi$$

(19)

where

$$\chi =-2i\lambda (dt{)}^{\left[{\displaystyle \frac{2}{f\left(\alpha \right)}}\right]-1}\mathit{ln}\Psi$$

(20)

is the complex scalar potential of the complex velocity fields (5) and $\Psi$ is the states function (on the significances of $\Psi$, see [11,12,13]. In this context, by substituting Equation (19) in Equation (16) and by employing the mathematical procedures from [14,25], the geodesics Equation (16) can be written as a multifractal Schrödinger-type equation:

$$2{\lambda }^2(dt{)}^{\left[{\displaystyle \frac{4}{f\left(\alpha \right)}}\right]-2}{\partial }^l{\partial }_l\Psi +i\lambda (dt{)}^{\left[{\displaystyle \frac{2}{f\left(\alpha \right)}}\right]-1}{\partial }_t\Psi =0$$

(21)

Therefore, for the complex velocity fields (19), the dynamics of any complex system are described through multifractal-type Schrödinger regimes (i.e., Schrödinger-type equations at various scale resolutions).

4. Nonlinear Behaviors in Complex Systems in the One-Dimensional Stationary Case

To explore the deeper structures embedded within the multifractal Schrödinger equation, we analyze its simplest form: the one-dimensional, stationary case. By separating variables, Equation (21) reduces to a familiar Helmholtz-like equation

$${\displaystyle \frac{d^2\Psi }{d{x}^2}}+k_0^2\Psi =0$$

(22)

with

$$k_0^2={\displaystyle \frac{E}{2m_0{\lambda }^2{\left(dt\right)}^{\left[\frac{4}{f\left(\alpha \right)}\right]-2}}}$$

(23)

In Equation (23), $E$ is the multifractal energy of the complex systems structural unit and $m_0$ is the rest mass of the complex system’s structural unit.

The solution of Equation (22) can be written as

$$\Psi \left(x\right)=h{e}^{i\left(k_{0}x+\theta \right)}+\acute{h}{e}^{-i\left(k_{0}x+\theta \right)}$$

(24)

where $h$ is the complex amplitude, $\acute{h}$ is the complex conjugate of $h$ and $\theta$ is a phase. Thus, $h$, $\acute{h}$ and $\theta$ label each structural unit from complex systems that has as a “fundamental property”, the same $k_0$.

Equation (22) has a “hidden” symmetry by means of a homographic group of multifractal type. Indeed, the ratio $\epsilon$ of two independent linear solutions of Equation (22) is a solution of Schwartz’s differential equation of multifractal type [26]:

$$\left\{\epsilon ,x\right\}={\displaystyle \frac{d}{dx}}\left({\displaystyle \frac{\ddot{\epsilon }}{\dot{\epsilon }}}\right)-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\ddot{\epsilon }}{\dot{\epsilon }}}\right)}^2=2k_0^2$$

(25)

$$\dot{\epsilon }={\displaystyle \frac{d\epsilon }{dx}},\ddot{\epsilon }={\displaystyle \frac{d^2\epsilon }{d{x}^2}}$$

(26)

The left part of (25) is invariant with respect to the homographic transformations of multifractal type:

$$\epsilon \leftrightarrow {\epsilon }^{\prime }={\displaystyle \frac{a\epsilon +b}{c\epsilon +d}}$$

(27)

with $a$, $b$, $c$, and $d$ real parameters (of multifractal type). The relation (27) corresponding to all possible values of these parameters defines the multifractal-type SL(2ℝ) group.

Thus, all the complex system’s structural units having the same $k_0$ are in biunivocal correspondence with the transformations of the multifractal-type SL(2ℝ) group. This allows the construction of a state parameter of multifractal type, $\epsilon$, for each complex system’s structural unit, separately. To this purpose, let us choose the general form of the solution of Equation (25), written as

$${\epsilon }^{\prime }=l+mtan\left(k_{0}x+\theta \right)$$

(28)

Thus, through $l$, $m$ and $\theta$ it is possible to characterize any complex system’s structural unit. In such a conjecture, identifying the phase from Equation (28) with the one from Equation (24), the state parameter of multifractal type becomes

$${\epsilon }^{\prime }={\displaystyle \frac{h+\overline{h}\epsilon }{1+h}},h=l+\mathfrak{I}m,\overline{h}=l-\mathfrak{I}m,\epsilon \equiv e^{2i\left(k_{0}x+\theta \right)}$$

(29)

The ratio ${\epsilon }^{\prime }$ serves as a coordinate that uniquely specifies the state of a given structural unit within the collective dynamics. It is not an intrinsic property of an isolated unit, but rather a relational coordinate that encodes the unit’s complex amplitude, $h$, and phase, $\theta$, within the geometric phase space defined by the SL(2ℝ) group.

Equation (29) provides an explicit mapping. The state parameter ${\epsilon }^{\prime }$ is a coordinate on the SL(2ℝ) manifold, and its value for any given structural unit is determined by the complex amplitude h of that unit’s wavefunction. All units sharing the same $k_0$ are described by states on the same SL(2ℝ) manifold, and ${\epsilon }^{\prime }$ is the coordinate that locates a specific unit on that manifold.

The fact that (28) is also a solution of Equation (25) implies, by explaining Equation (27), the multifractal-type SL(2ℝ) group [12,17,25]:

$$h^{\prime }={\displaystyle \frac{ah+b}{ch+d}},\overline{h}={\displaystyle \frac{a\overline{h}+b}{c\overline{h}+d}},k^{\prime }={\displaystyle \frac{c\overline{h}+d}{ch+d}}k$$

(30)

Therefore, the group (30) works as synchronization modes among the various structural units of any complex system, process to which the amplitudes and phases of each of them obviously participate, in the sense that they are also connected. More precisely, through the group (30), the phase of $k$ is only moved with a quantity depending on the amplitude of the complex system’s structural units at the transition among various structural units. Furthermore, the amplitude of the structural unit of any complex systems is also affected from a homographic perspective. The usual synchronization manifested through the delay of the amplitudes and phases of the complex system’s structural units must represent here a particular case.

The structure of group (30) is typical of SL(2ℝ), which will be taken in the standard form:

$$\left[A_1,A_2\right]=A_1,\left[A_2,A_3\right]=A_3,\left[A_3,A_1\right]=-2A_2$$

(31)

where $A_k,$ $k=\mathrm{1,2},3$ are the infinitesimal generators of the group. Because the group is simple transitive, these generators can be easily found as the components of the multifractal-type Cartan coframe, from the relation

$$d\left(f\right)=\sum {\displaystyle \frac{\partial f}{\partial x^k}}d{x}^k=\left\{{\omega }^1\left[h^2{\displaystyle \frac{\partial }{\partial h}}+{\overline{h}}^2{\displaystyle \frac{\partial }{\partial \overline{h}}}+\left(h-\overline{h}\right)k{\displaystyle \frac{\partial }{\partial k}}\right]+2{\omega }^2\left(h{\displaystyle \frac{\partial }{\partial h}}+\overline{h}{\displaystyle \frac{\partial }{\partial \overline{h}}}\right)+{\omega }^3\left({\displaystyle \frac{\partial }{\partial h}}+{\displaystyle \frac{\partial }{\partial \overline{h}}}\right)\right\}\left(f\right)$$

(32)

where ${\omega }^k$ are the components of the multifractal-type Cartan coframe to be found from the system:

$$dh={\omega }^1{h}^2+2{\omega }^{2}h+{\omega }^3,d\overline{h}={\omega }^1{\overline{h}}^2+2{\omega }^2\overline{h}+{\omega }^3,dk={\omega }^{1}k\left(h-\overline{h}\right)$$

(33)

In this way we obtained both the infinitesimal generators and the multifractal coframe, by identifying the right-hand side of Equation (32) with the standard dot product of the SL(2ℝ) algebra:

$${\omega }^1{A}_3+{\omega }^3{A}_1-2{\omega }^2{A}_2$$

(34)

so that

$$A_1={\displaystyle \frac{\partial }{\partial h}}+{\displaystyle \frac{\partial }{\partial \overline{h}}},A_2=h{\displaystyle \frac{\partial }{\partial h}}+\overline{h}{\displaystyle \frac{\partial }{\partial \overline{h}}},A_3=h^2{\displaystyle \frac{\partial }{\partial h}}+{\overline{h}}^2{\displaystyle \frac{\partial }{\partial \overline{h}}}+\left(h-\overline{h}\right)k{\displaystyle \frac{\partial }{\partial k}}$$

(35)

and

$${\omega }^1={\displaystyle \frac{dk}{\left(h-\overline{h}\right)k}},{2\omega }^2={\displaystyle \frac{dh-d\overline{h}}{h-\overline{h}}}-{\displaystyle \frac{h+\overline{h}}{h-\overline{h}}}{\displaystyle \frac{dk}{k}},{\omega }^3={\displaystyle \frac{hdh-\overline{h}dh}{h-\overline{h}}}+{\displaystyle \frac{h\overline{h}dk}{\left(h-\acute{h}\right)k}}$$

(36)

In the following we will not use the previous differential forms, but the absolute invariant differentials:

$${\omega }^1={\displaystyle \frac{dh}{\left(h-\overline{h}\right)k}},{\omega }^2=-i\left({\displaystyle \frac{dk}{k}}-{\displaystyle \frac{dh+d\overline{h}}{h-\overline{h}}}\right),{\omega }^3={\displaystyle \frac{kd\overline{h}}{h-\overline{h}}}$$

(37)

The advantage of this representation is that it makes obvious the connection with the Poincaré representation of the Lobachevsky plane. Indeed, the metric here is as follows:

$${\displaystyle \frac{d{s}^2}{g}}={\left({\omega }^2\right)}^2-4{\omega }^1{\omega }^2={\left({\displaystyle \frac{dk}{k}}-{\displaystyle \frac{dh+d\overline{h}}{h-\overline{h}}}\right)}^2+4{\displaystyle \frac{dhd\overline{h}}{{\left(h-\overline{h}\right)}^2}}$$

(38)

where $g$ is a constant.

These metrics reduce to the Poincaré metrics in the case of ${\omega }^2=0$, which defines the variable $\theta$ as the angle of parallelism (in Levi-Civita sense) of the multifractal-type hyperbolic plane.

Returning to the homographic transformation (27), taking into account the previous presented implications of this transformation, we can observe that each structural unit of any complex system can be located either for homogenous coordinates $\left(a,b,c,d\right)$, or for three non-homogenous coordinates, when a parallelism of direction in the Levi-Civita sense becomes functional on the manifold induced by the multifractal-type SL(2ℝ) group. Now, the simultaneity condition of the complex system’s free structural units can be differently characterized from a multifractal-type Riccati equation in pure differentials (this shall be named the multifractal-type Riccati gauge) [27,28]:

$$d{\displaystyle \frac{a\epsilon +b}{c\epsilon +d}}=0$$

(39)

which implies

$$d\epsilon ={\omega }^1{\epsilon }^2+{\omega }^2\epsilon +{\omega }^3$$

(40)

where ${\omega }^1$, ${\omega }^2$, and ${\omega }^3$ are the components of the multifractal-type Cartan coframe given by Equation (36). Consequently, to characterize the dynamics of any complex system dynamics as a succession of states of an ensemble of simultaneous structural units, as it were, it suffices to have three differentiable 1-forms, representing a coframe of a multifractal-type SL(2ℝ) algebra. Therefore, a state of a complex system in specific dynamics can be organized as a metric plane space, i.e., a multifractal-type Riemannian three-dimensional space. Thus, the geodesics of such a Riemannian space are given by some conservations of multifractal-type equations:

$${\omega }^1=a^{1}d\tau ,{\omega }^2=a^{2}d\tau ,{\omega }^3=a^{3}d\tau$$

(41)

where $a^1$, $a^2$, and $a^3$ are constant and $\tau$ is the affine parameter of the geodesics, so that along these geodesics of differential equation, Equation (40) is a Riccati-type ordinary differential:

$${\displaystyle \frac{d\epsilon }{d\tau }}=a^1{\epsilon }^2+2a^2\epsilon +a^3$$

(42)

Let the following form of the previous equation be considered:

$$A{\displaystyle \frac{d\epsilon }{d\tau }}-{\epsilon }^2+2B\epsilon +AC=0$$

(43)

where

$${\displaystyle \frac{1}{a^1}}=A,-2{\displaystyle \frac{a^2}{a^1}}=B,-{\displaystyle \frac{a^3}{a^1}}=AC$$

(44)

Since the roots of the polynomial

$$P\left(\epsilon \right)={\epsilon }^2-2B\epsilon -AC$$

(45)

can be written in the form

$${\epsilon }_1=B+iA\Omega ,{\epsilon }_2=B-iA\Omega ,{\Omega }^2={\displaystyle \frac{C}{A}}-{\left({\displaystyle \frac{B}{A}}\right)}^2$$

(46)

the change in variable

$$z={\displaystyle \frac{\epsilon -{\epsilon }_1}{\epsilon -{\epsilon }_2}}$$

(47)

transforms in

$$\acute{z}=2i\Omega z$$

(48)

of solution

$$z\left(\tau \right)=z\left(0\right)e^{2i\Omega \tau }$$

(49)

Therefore, if the initial condition $z\left(0\right)$ is conveniently expressed, then it is possible to construct the general solution of Equation (42), by writing the transformation (47) in the form:

$$\epsilon ={\displaystyle \frac{{\epsilon }_1+r{e}^{2i\Omega \left(\tau -{\tau }_0\right)}{\epsilon }_2}{1+r{e}^{2i\Omega \left(\tau -{\tau }_0\right)}}}$$

(50)

where $r$ and ${\tau }_0$ are two integration constants. Using Equation (46), it is possible to write this solution in real terms:

$$z=B+A\Omega \left\{{\displaystyle \frac{2rsin\left[2\Omega \left(\tau -{\tau }_0\right)\right]}{1+r^2+2rcos\left[2\Omega \left(\tau -{\tau }_0\right)\right]}}+i{\displaystyle \frac{1-r^2}{1+r^2+2rcos\left[2\Omega \left(\tau -{\tau }_0\right)\right]}}\right\}$$

(51)

Therefore, synchronization modes in phase and amplitude of the complex system’s structural units imply group invariances of SL(2ℝ) type. Then, double period dynamics, damped dynamics, modulated dynamics, chaotic dynamics, etc., emerge as natural behaviors in complex systems dynamics [29,30].

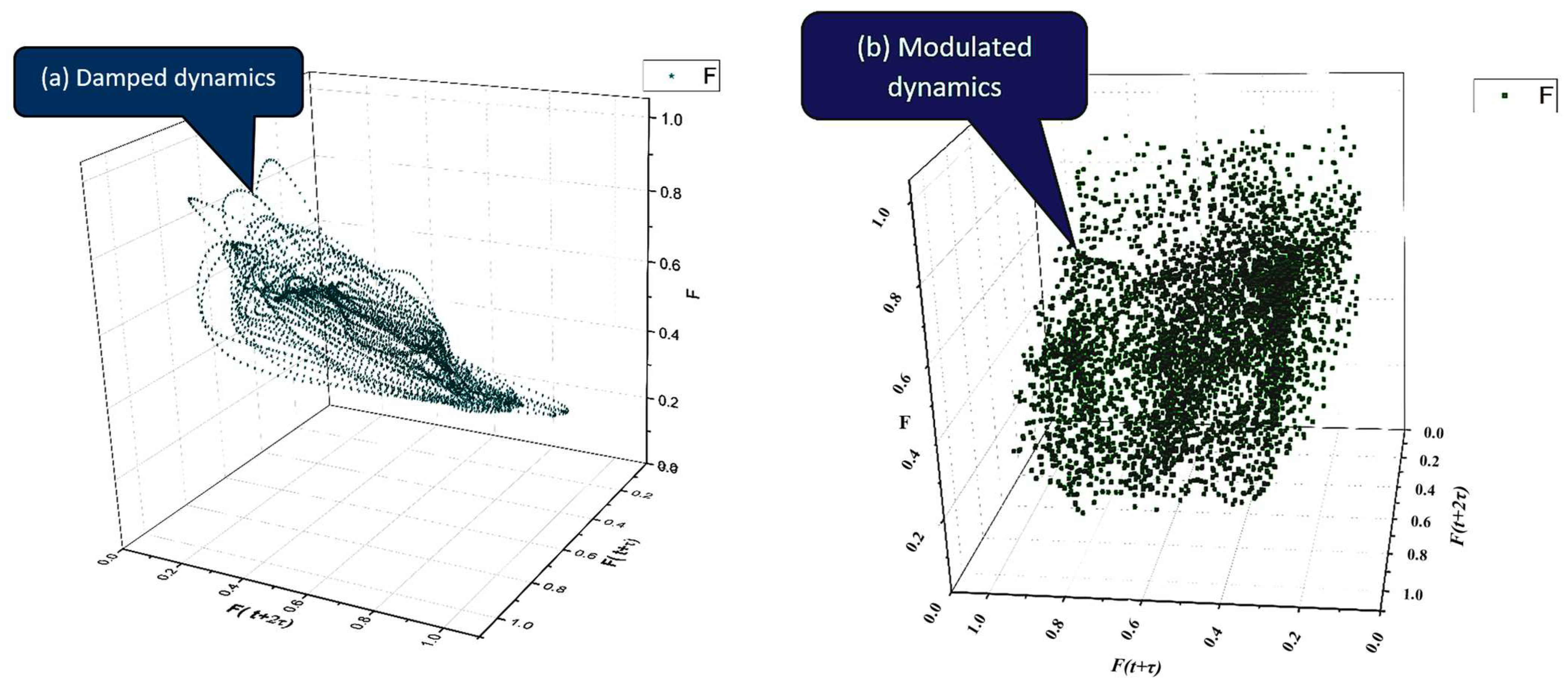
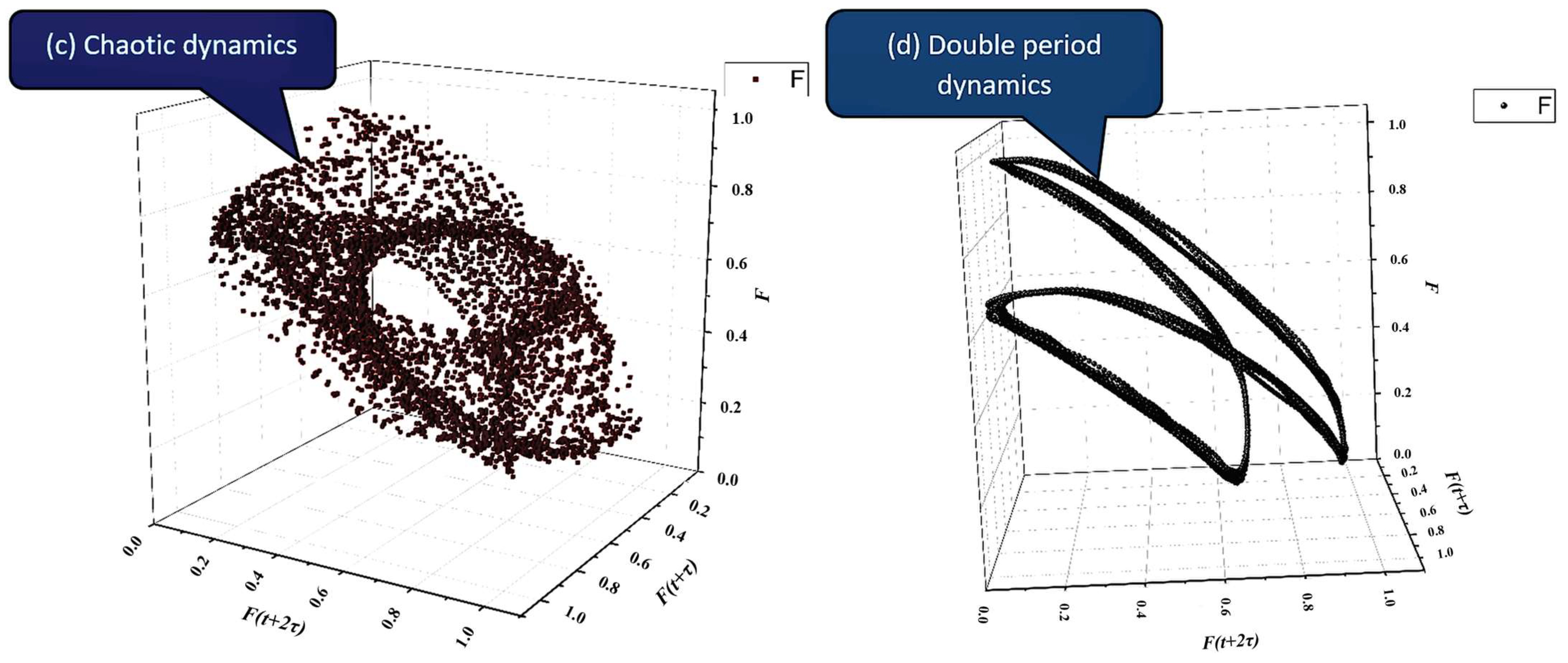
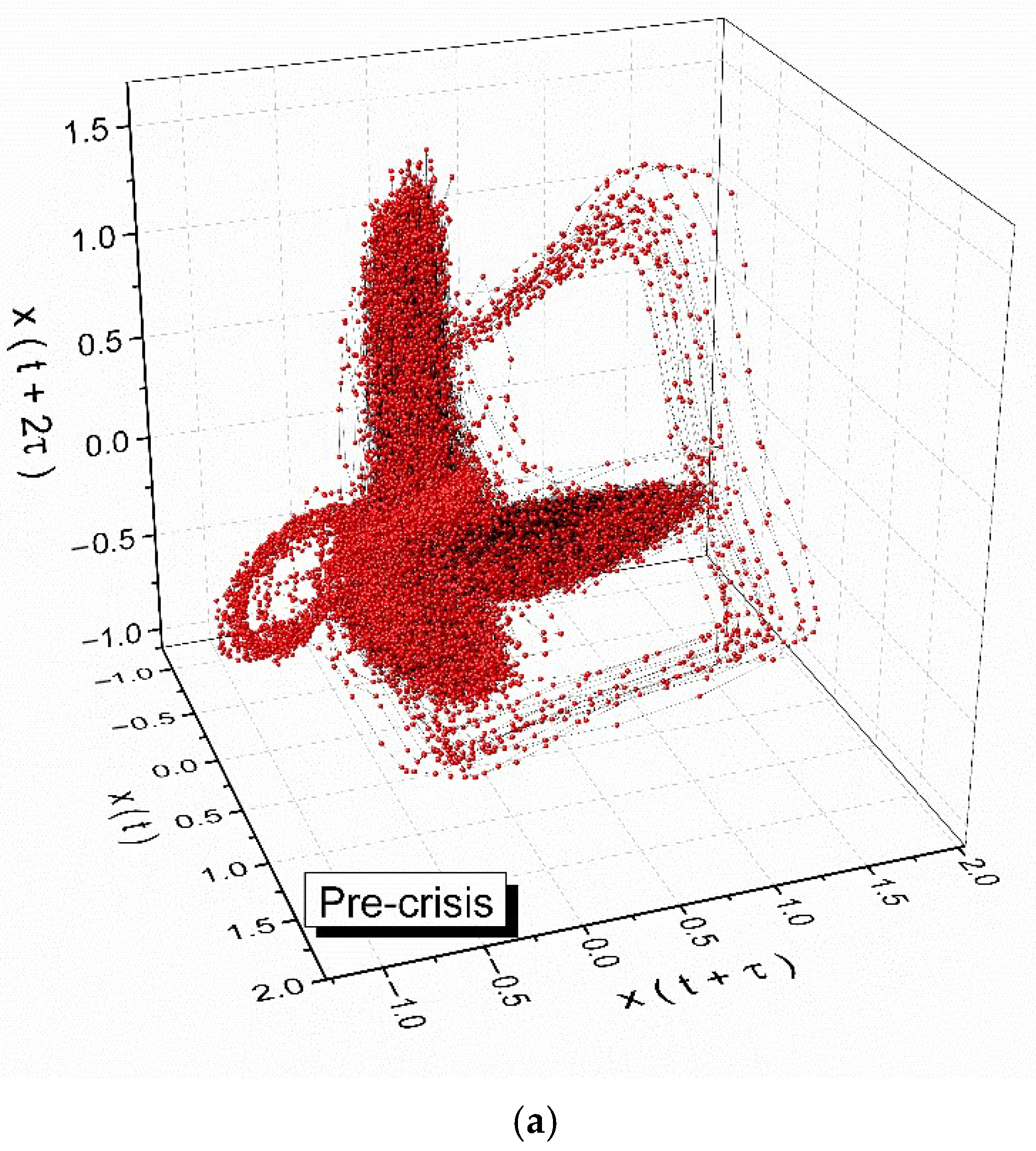
In Figure 1a–d we present the specific attractors within the phase space (reconstructed using the delay time approach) for various complex systems dynamics, based on Equation (51).

Equation (51) solutions were computed by substituting parameter sets ($A,B,\Omega ,\tau )$ into $F\left(\Omega ,\tau =time\right)\equiv {\displaystyle \raisebox{1ex}{$\left(z-B\right)$}\!\left/ \!\raisebox{-1ex}{$A$}\right.}$. Each regime arises from distinct parameter ranges: damped dynamics occur when $\Omega$ is real and positive with B > 0; modulated dynamics arise from small imaginary parts in $\Omega$; chaotic dynamics emerge for nonlinear coupling terms; double-period dynamics appear when two commensurate frequencies coexist (See

Table 1. Parameter sets ($A,B,\Omega ,\tau )$ for each dynamic regime in Figure 1.

Regime	A	B	$\mathit{\Omega }$	$\mathit{\tau }$
Damped	1.0	0.5	1.2	0.8
Modulated	1.0	0.5	1.2 + 0.1i	0.8
Chaotic	1.0	0.5	complex	varies
Double-period	1.0	0.5	0.8	1.6

for exact parameter values used for Figure 1a–d).

5. Discussions

5.1. Broader Implications of Our Model

Our multifractal model, grounded on Scale Relativity Theory (SRT), reveals extensive relevance across several scientific fields, encapsulating the intricate behavior of complex systems that display damped, modulated, chaotic, and double-period dynamics. Below, we present several scientific domains where, in our opinion, our model can be applied in order to better understand the various dynamics involved. For each dynamic regime, we will first reiterate the mathematical condition from the model and then provide a detailed, mechanistic interpretation for one key example.

5.1.1. Damped Dynamics in Neural Systems

In biology, damped dynamics are prominently observed in neural systems where oscillatory activities, such as gamma-band rhythms, decay following neuronal excitation. These dynamics are critical for processes like sensory integration and motor control. Recent electrophysiological research using multifractal techniques highlights the significant role of damped oscillations in cortical regions, providing insights into neural recovery mechanisms after intense neuronal activities [31,32].

Model Link: Damped dynamics in the model correspond to a solution with a real frequency $\Omega$ and a positive damping parameter B. The trajectory in phase space is a spiral that converges to a stable fixed point.

Mechanistic Mapping: In neuroscience, local populations of neurons frequently exhibit damped oscillations in response to a transient stimulus. This phenomenon is not merely incidental; it is a critical feature of stable neural processing, representing the circuit’s ability to process information and then quickly return to a baseline resting state, ready for the next input. We can propose a direct mechanistic mapping between our model and this process. The stable fixed-point of the attractor represents the neural circuit’s homeostatic baseline firing rate. An external stimulus, such as a sensory input, perturbs the system away from this fixed point, initiating an oscillation. The parameter B in our model, which governs the rate of damping, can be interpreted as the effective strength of inhibitory feedback within the neural circuit (e.g., the gain of recurrent inhibitory interneurons). This feedback is the physiological mechanism responsible for quenching the post-stimulus oscillations and ensuring the network remains stable and does not descend into runaway excitation. Thus, our model parameter B is not just an abstract number but a representation of a key physiological quantity: the efficacy of synaptic inhibition.

5.1.2. Modulated Dynamics and Theta-Gamma Coupling in the Brain

In neurobiology, modulated dynamics are exemplified by cross-frequency modulation such as theta-gamma coupling, fundamental in memory encoding and attention mechanisms. Multifractal analysis provides nuanced insights into these modulation patterns, enhancing our understanding of neural processing and potential implications for neurological disorders like schizophrenia and epilepsy [33,34].

Model Link: Modulated dynamics emerge from the model when the frequency parameter $\Omega$ is a complex number, $\Omega ={\Omega }_r+i{\Omega }_i$. This mathematical form naturally produces a high-frequency carrier wave, ${\Omega }_r$, whose amplitude is modulated by a lower-frequency envelope, ${\Omega }_i$.

Mechanistic Mapping: This mathematical structure is a direct and compelling analog of cross-frequency phase-amplitude coupling, a ubiquitous phenomenon in the brain that is strongly implicated in cognitive functions like working memory and information routing. The most studied example is theta-gamma coupling, where the phase of a slow theta rhythm (4–12 Hz) modulates the amplitude (power) of a fast gamma rhythm (30–100 Hz) [33,34]. Our model offers a novel, first-principles explanation for the origin of such signals. We propose a direct mapping: the real part of our frequency, ${\Omega }_r$, corresponds to the fast gamma oscillation, generated by local excitatory–inhibitory loops. The imaginary part, ${\Omega }_i$, corresponds to the slower, modulating theta rhythm, often driven by subcortical inputs from structures like the hippocampus or thalamus. In this view, theta-gamma coupling is not an ad hoc phenomenon but a natural mode of oscillation for any system governed by the underlying SL(2ℝ) symmetry of multifractal dynamics. This elevates the connection from a simple analogy to a proposed fundamental principle for the emergence of complex neural codes.

5.1.3. Chaotic Dynamics in Gene Regulatory Networks (GRNs)

Biological systems frequently display chaotic dynamics, particularly within gene regulatory networks where intricate feedback loops can lead to chaotic gene expression patterns. Recent multifractal analyses have offered insights into these regulatory mechanisms, improving our understanding of developmental biology and genetic disorder pathogenesis, and opening pathways for innovative therapeutic interventions [35,36].

Model Link: The chaotic regime in our model is characterized by a strange attractor, representing bounded, aperiodic dynamics that are highly sensitive to initial conditions.

Mechanistic Mapping: While once thought to be detrimental, chaotic dynamics are now understood to play a potential role in cellular adaptability and differentiation. Crucially, research shows that chaos in GRNs is not random but arises from specific network architectures, particularly the competition between multiple negative and positive feedback loops or different oscillatory modes [35,36]. The strange attractor generated by our model can be interpreted as the geometric representation of the system’s state (i.e., the vector of protein concentrations) as it moves aperiodically between the basins of attraction of these competing regulatory modes. The complex parameters of the chaotic solution in our model reflect the intricate, finely tuned balance of activation and inhibition rates within the GRN. This balance prevents the system from settling into a simple periodic behavior (like a cell cycle) and instead allows it to explore a wide range of expression states, a behavior that could be crucial for processes like developmental plasticity or searching for optimal responses to novel environmental stressors.

5.1.4. Double-Period Dynamics in Predator-Prey Systems

Double-period dynamics are clearly illustrated in biological systems via predator-prey interactions that frequently display alternating cycles of population abundance. Multifractal analysis has elucidated the dynamics and interdependencies within complex ecological systems, offering powerful instruments for ecological forecasting and biodiversity management [37,38].

Model Link: This regime is characterized by a phase-space attractor with two distinct lobes, the result of a period-doubling bifurcation.

Mechanistic Mapping: The cyclic rise and fall of predator and prey populations is a classic topic in ecology, often described by Lotka-Volterra equations. It is well-established that as ecological parameters are varied, these systems can undergo a series of period-doubling bifurcations, a classic route to chaos [37,38]. Our model’s double-period solution represents a fundamental pattern that mirrors these ecological phenomena. The transition from a single-period limit cycle (a simple annual cycle) to a double-period one in our model, which is achieved by tuning a parameter like $\tau$ can be mechanistically mapped to a change in a key ecological rate. For example, an increase in the predator’s hunting efficiency or a change in the prey’s reproductive rate due to environmental factors can push the system across a bifurcation threshold, leading to a stable two-year cycle instead of a one-year cycle. Our model thus captures a universal dynamic pattern that is independent of the specific species involved, suggesting that such bifurcations are a fundamental property of interacting populations governed by scale-dependent dynamics.

5.2. An Application of Our Model

In what follows, we will present a practical application of our model, highlighting the transition from regular to chaotic dynamics in physiological pathological processes.

To this purpose, we conducted an analysis on electrocardiograms obtained from the PhysioNet database. This database provides open access to a comprehensive collection of physiological signals [39,40,41] obtained from a diverse group of patients. It also offers specialized software for the visualization and analysis of these signals. It is freely accessible under the Open Data Commons Public Domain Dedication and License v1.0 (PDDL). Available resources are provided to encourage ongoing research in the field of analyzing intricate biomedical and physiological data.

The signal we examined possesses the subsequent characteristics: The recording has a duration of approximately 3 h, with a sampling interval of 4 milliseconds and a sampling rate of 250 recordings per second. It consists of a total of 9,205,760 data points, with amplitudes ranging from −0.6 millivolts to 0.9 millivolts.

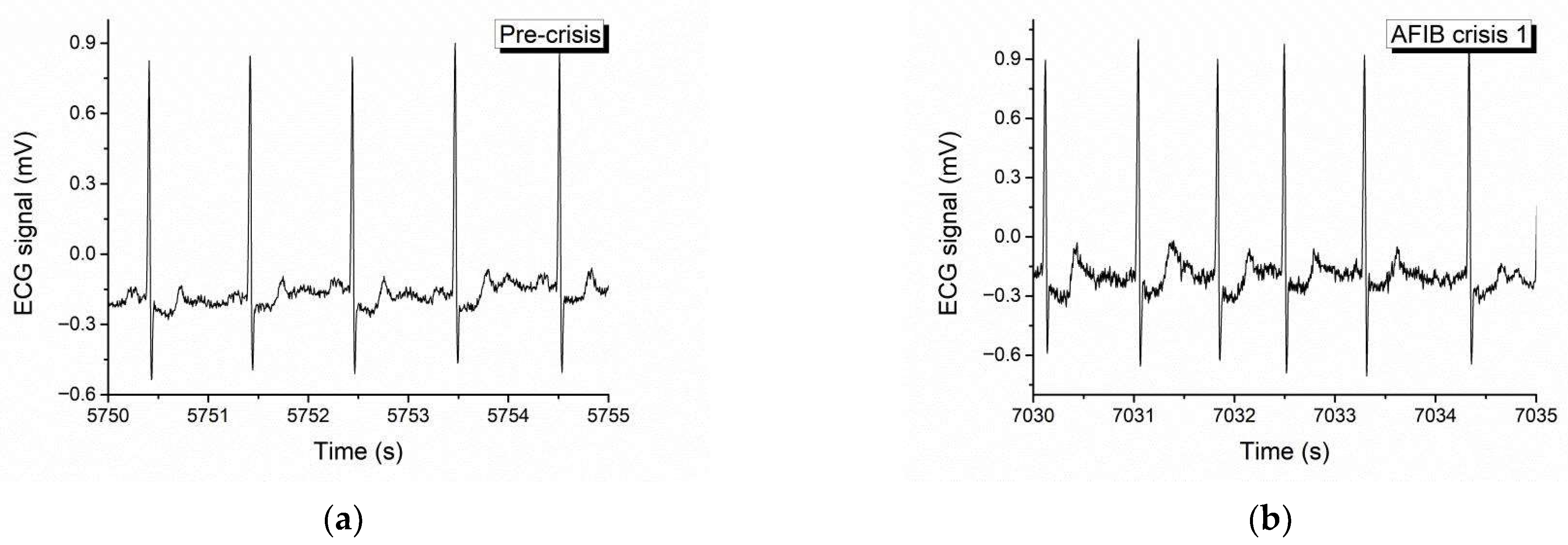
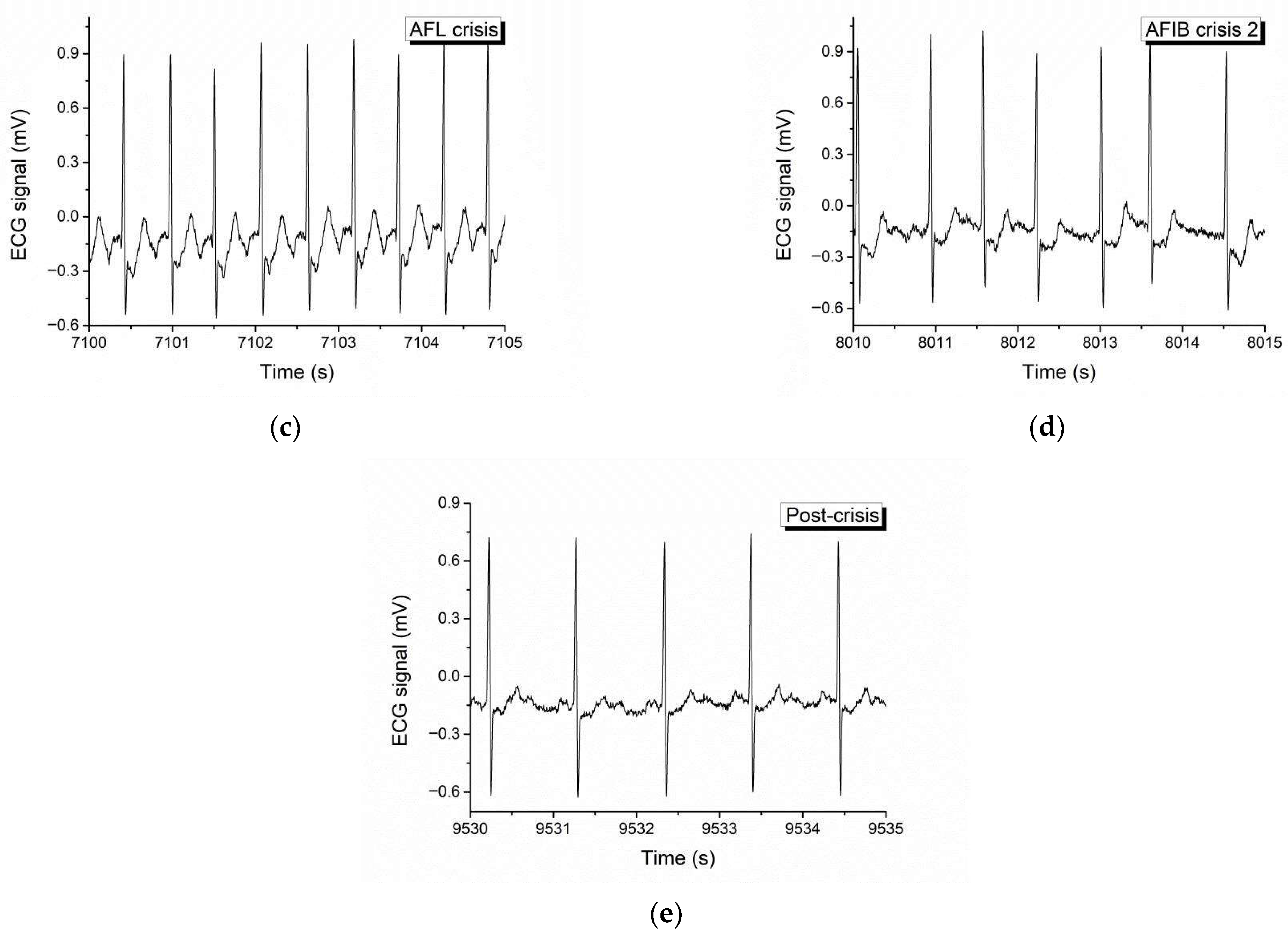
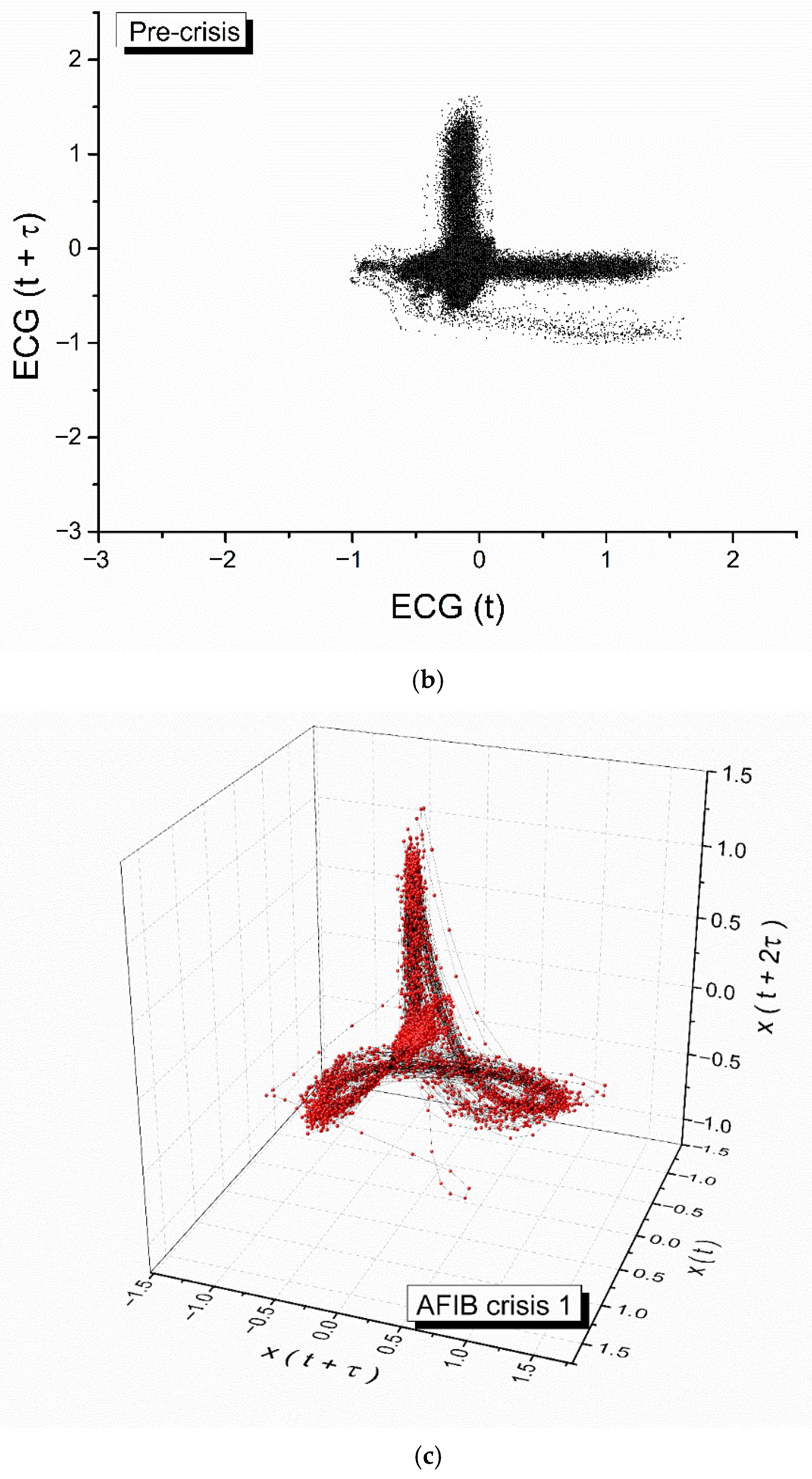
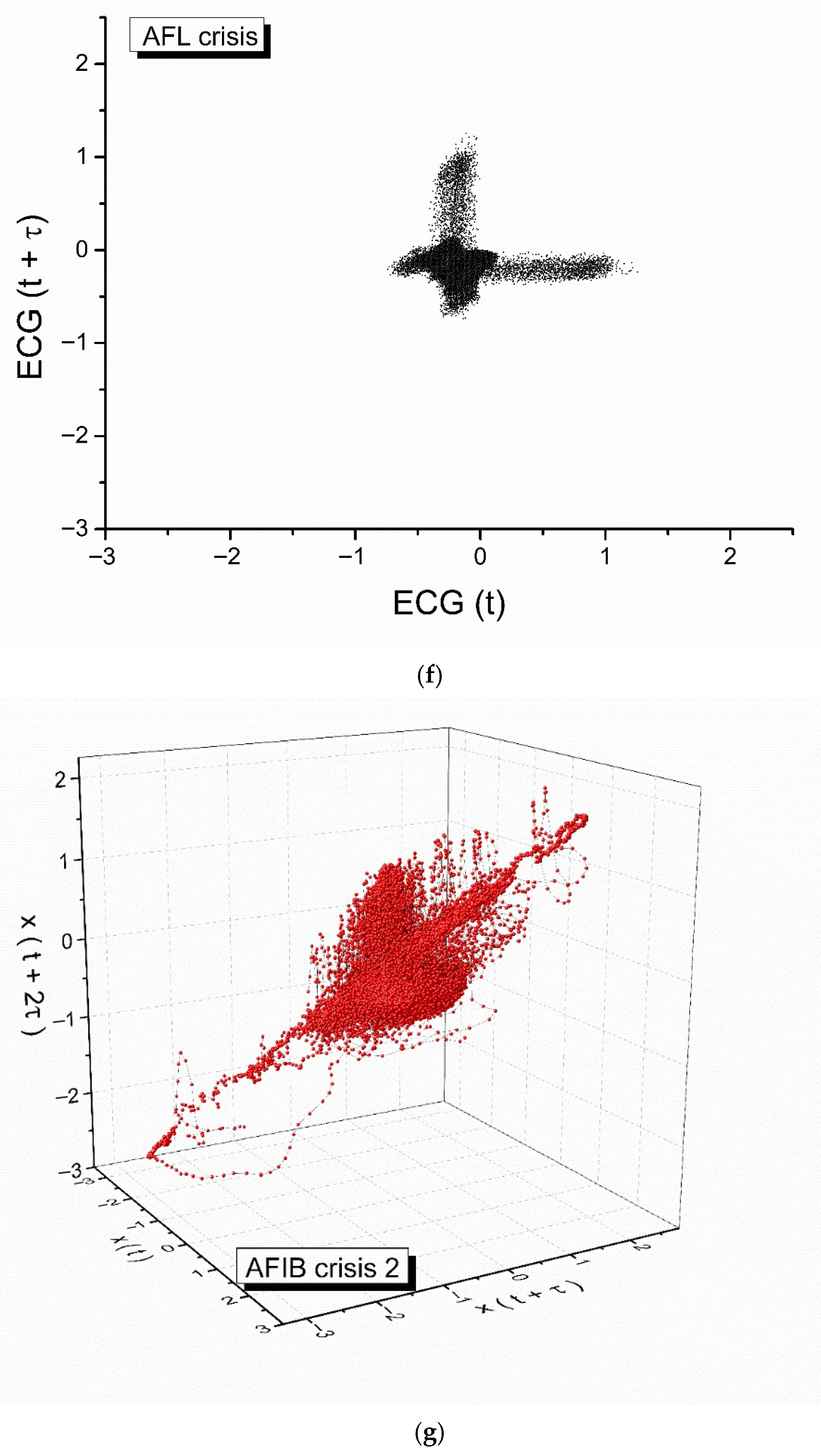
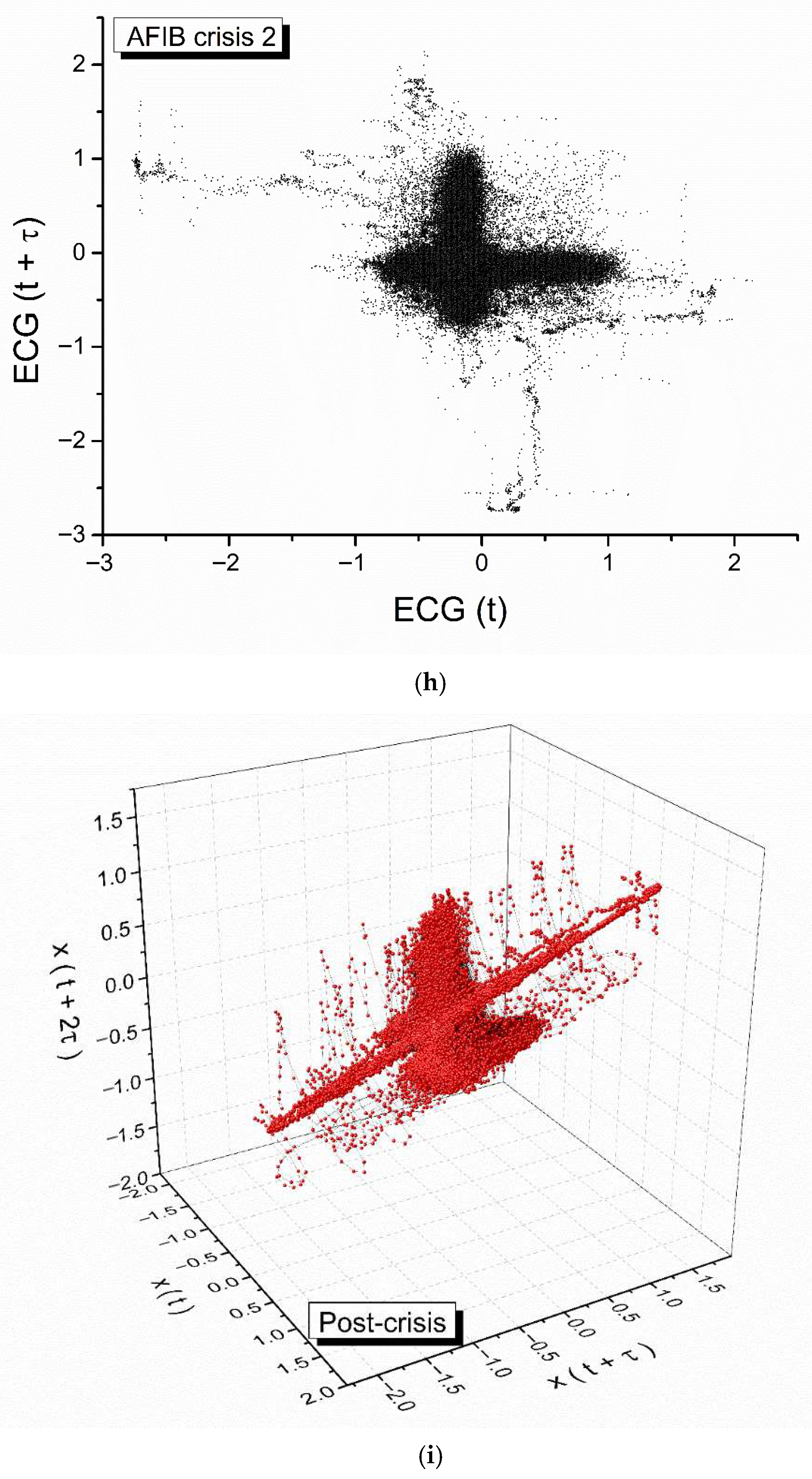
Figure 2 depicts the examination of the 1/R-R interval, which represents a single cardiac cycle. The analysis reveals three instances of crises, consisting of two atrial fibrillations and one flutter fibrillation. The analysis includes ECG fragments of 5 s each, representing the pre-crisis, first atrial fibrillation (AFIB), atrial flutter (AFL), second AFIB, and post-crisis periods.

During both the pre-crisis and post-crisis periods, the signals remain within the expected range. During the initial episode of atrial fibrillation (AFIB), the heart rate gradually rises, followed by a sudden surge in atrial flutter (AFL), and then gradually decreases again in the subsequent episode of AFIB.

We show in Figure 3 a breakdown of the ECG fragments.

By employing the auto-correlation function, we developed specific attractors within the phase space (reconstructed using the delay time approach) for each stage of the heart dynamics: pre-crisis, AFIB crises 1 and 2, AFL crisis and post-crisis. These attractors and the corresponding 2D maps are shown in Figure 4.

After we built the attractors and generated the corresponding 2D maps, we were able to calculate the Hurst exponents and fractal dimensions for each stage. They are presented in

Table 2. The calculated Hurst exponents for each stage of the heart dynamics.

Stage	Hurst Exponent	Fractal Dimension
Pre-crisis	0.7739	0.2261
AFIB crisis 1	0.6772	0.3228
AFL crisis	0.6680	0.332
AFIB crisis 2	0.7871	0.2129
Post-crisis	0.8390	0.161

.

As can be seen from Table 2, the Hurst exponent for all the stages is subunitary. These results are consistent with other published works, such as the ones from [42,43]. The fact that these Hurst exponent values are always larger than 0.5 shows the existence of long-range, self-similar, persistent correlations, that extended over all the analyzed cardiac dynamics.

Furthermore, we can observe, by means of the fractal dimension variation, that the physical processes (in our case, atrial fibrillations) that disrupt the normal functioning of the heart produce a fractal pattern in time. The largest fractal dimension is present in the AFL crisis, and the lowest obtained values are present in pre- and post-crisis, respectively. These facts show that the cardiac dynamics are strongly chaotic during the AFL crisis, while before and after the crisis, these dynamics tend to have a more regular behavior.

5.3. Limitations and Future Directions

A critical assessment of the proposed model requires an honest appraisal of its current limitations. These limitations, far from invalidating the approach, serve to highlight the most promising and necessary directions for future theoretical development.

5.3.1. Sensitivity to the Choice of Fractal Dimension

In the derivation of the scale covariant derivative (Equation (13)), we made a significant simplification by assuming a Markovian process, which effectively collapses the full multifractal spectrum $f\left(\alpha \right)$ to a single, constant fractal dimension, $D_F$ (Equation (12)). The choice of this parameter is physically significant; as previously noted, a value of $D_F<2$ is typically associated with persistent or correlative processes, while $D_F>2$ is associated with anti-persistent or non-correlative processes [14,19].

A significant limitation of the current analysis is that this value was treated as a given constant. In any rigorous application to a real-world system, the effective fractal dimension $D_F$ should not be an assumption but should be determined empirically from the data itself. Standard techniques such as Multifractal Detrended Fluctuation Analysis (MFDFA) are well-suited for this purpose, as they can extract the scaling exponents from a time series [44].

More fundamentally, the reduction to a single $D_F$ discards the rich information contained in the full multifractal spectrum. In future work, we will aim to re-introduce the singularity spectrum $f\left(\alpha \right)$ into the covariant derivative (Equation (9)). This would transform the constant diffusion coefficient $\lambda$ into a state-dependent function, $\lambda \left(\alpha \right)$, leading to a far more complex and realistic description of the system’s dynamics. Such a model could account for the fact that the nature of the “fractal diffusion” may vary depending on the local regularity of the system’s trajectory.

5.3.2. Extension to Higher-Dimensional and Non-Stationary Systems

The detailed analytical solution for the system’s attractors presented in this work was derived for a one-dimensional, stationary case. While this provides invaluable insight into the underlying principles, most complex systems of interest are neither one-dimensional nor stationary. Extending the framework to higher dimensions and time-dependent scenarios is a primary goal for our future research, but one that presents significant and non-trivial challenges.

An extension to higher dimensions is not straightforward. The SL(2ℝ) symmetry identified here is specific to the geometry of the one-dimensional problem. A higher-dimensional generalization, such as for 3D fluid dynamics, would require identifying the appropriate higher-rank symmetry group (e.g., SL(n,ℝ)) and developing the corresponding geometric formalism for the state space. This is a formidable mathematical task.

Furthermore, the mathematical literature on higher-dimensional multifractal analysis reveals that the structure of the problem changes fundamentally. The domain of the multifractal spectrum in higher dimensions is no longer a simple interval but can be a non-convex set, potentially with an empty interior [45,46]. This increased complexity would necessitate a fundamental generalization of the scale covariant derivative itself, as the simple power-law dependence on a single $D_F$ would no longer be sufficient. Similarly, addressing non-stationary systems, where the statistical properties change over time, would require a time-dependent formulation of the model’s parameters, likely leading to a scenario where the system evolves between different attractor geometries. These challenges underscore the fact that the present work is a foundational step, providing a proof of principle that can be built upon to tackle the full complexity of real-world systems.

6. Conclusions

The main conclusions of the present paper are the following:

• In traditional differential geometry, particle trajectories are represented by smooth, differentiable geodesics. By contrast, this manuscript considers particle motions as continuous but non-differentiable multifractal curves. Hence, the concept of geodesics is generalized to accommodate fractal structures, significantly broadening the scope of differential geometric analysis.
• The multifractal nature of the space–time geometry addressed in SRT necessitates replacing classical differential equations with fractal stochastic differential equations. These equations represent an advanced generalization of the classical equations used in differential geometry, incorporating stochasticity and scale-dependence explicitly into geometric and dynamic descriptions.
• The manuscript introduces scale-covariant derivatives, a generalization of the covariant derivatives of classical differential geometry. These derivatives account for variations in physical properties across scales, which classical geometries typically ignore. This approach ensures that the descriptions remain consistent and invariant under changes in scale, reflecting fractal and multifractal scaling symmetries.
• Classical differential geometry extensively uses symmetry groups (e.g., Lie groups) to describe geometric structures and transformations. Similarly, this manuscript applies multifractal analogs of classical groups (particularly the SL(2ℝ) group), identifying hidden symmetries that synchronize structural units within complex systems. Such symmetry groups facilitate an elegant and powerful geometric understanding of multifractal systems.
• The metric structure and affine connections, fundamental in classical differential geometry, are generalized to multifractal contexts. These generalized metrics, such as the multifractal-type metrics mentioned in the manuscript, permit consistent geometric interpretations of non-differentiable manifolds, enabling an enriched exploration of space-time structure and complex dynamics.