Mathematical Perspectives of a Coupled System of Nonlinear Hybrid Stochastic Fractional Differential Equations
Abstract
1. Introduction
1.1. Fractional Calculus
1.2. Coupled System and Hybrid Differential Equations
1.3. Related Literature to the Study
1.4. New Findings
- We introduce the idea of coupling neutral DEs with hybrid stochasticity, thereby advancing research in new directions by formulating a more realistic and mathematically enriched model.
- By incorporating hybrid differential structures, our model accounts for both continuous dynamics and discrete regime-switching behavior.
- Instead of relying on traditional fractional derivatives, which involve singular kernels and associated limitations, we employ the ABC derivative with a non-singular Mittag-Leffler kernel.
- We establish the mean-square Mittag-Leffler stability of the proposed system, ensuring that solutions remain bounded and decay predictably under stochastic fluctuations.
- To the best of our knowledge, mean-square stability analysis for both simple and coupled systems of FSDEs has not yet been investigated.
2. Preliminaries
- The functions satisfy with .
- The drift and diffusion terms satisfy
- Linear growth conditions hold: .
3. Results of Existence
- For
- For :
- For the stochastic term,
- We use the term from (12) instead of in the Itô calculus for simplicity.
- Putting these in the original equation, we get
3.1. Results with Lipschitz Coefficients
- Similarly, for the mild solution ,
3.2. Results Without Lipschitz Conditions
- Existence: Using Lemma (4), we represent and as the limit of the sequences and . Now, in Lemma (4), as , the RHS of (21) becomes
- Uniqueness: Assume that are two mild solutions of Equation (6). Using Lemma (4), we obtain the estimate
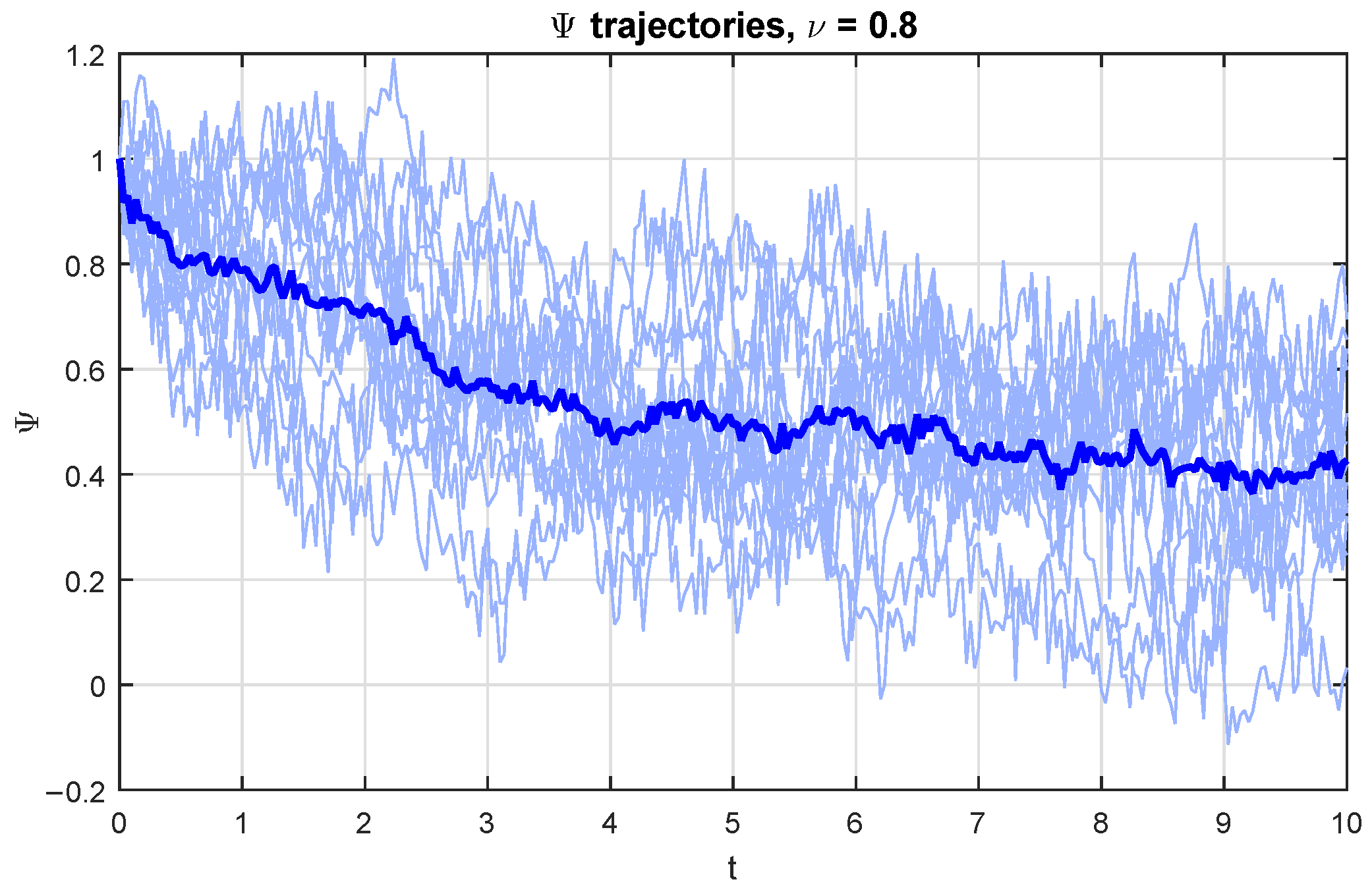
4. Mean-Square Mittag-Leffler Stability Analysis
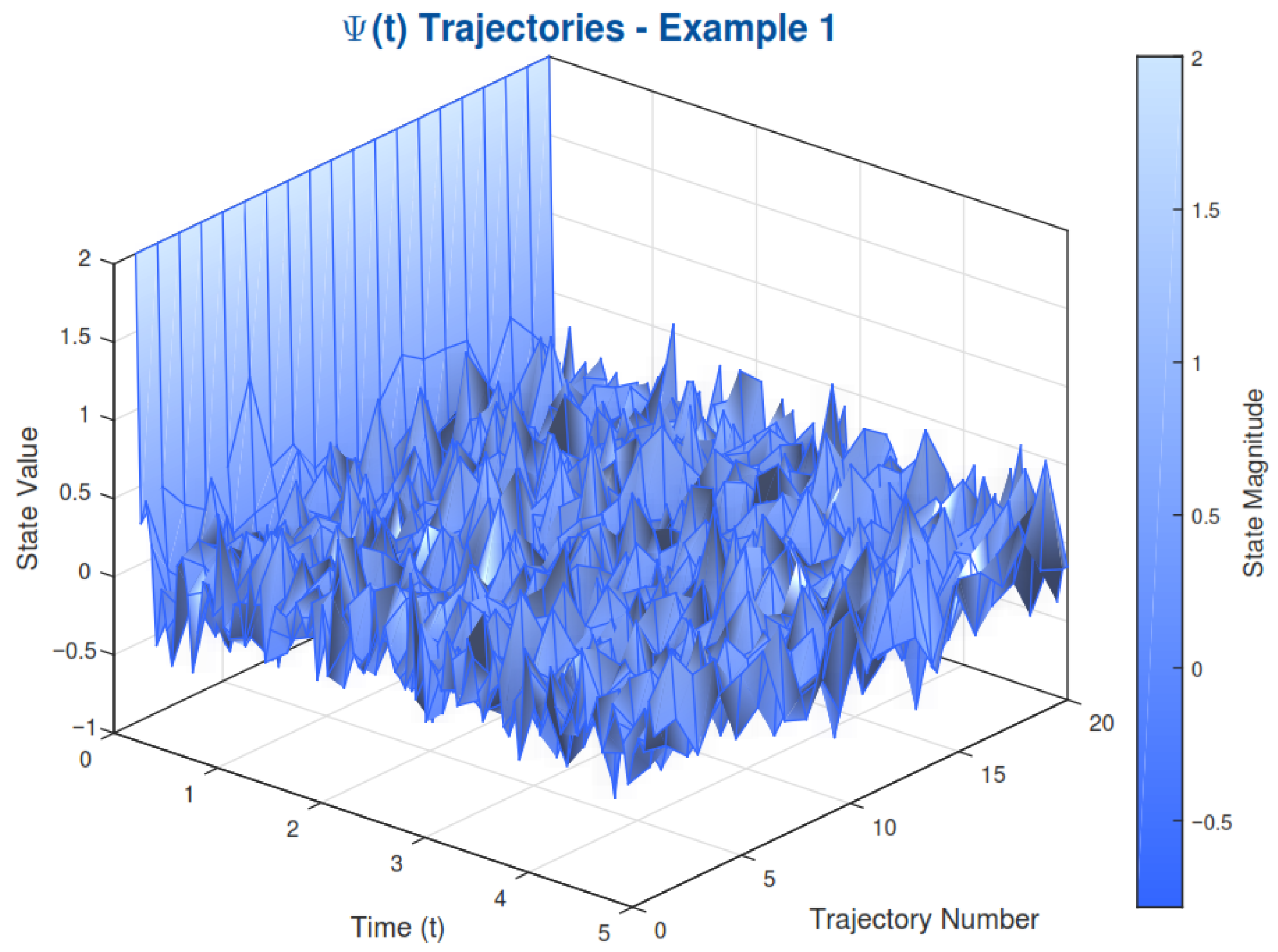
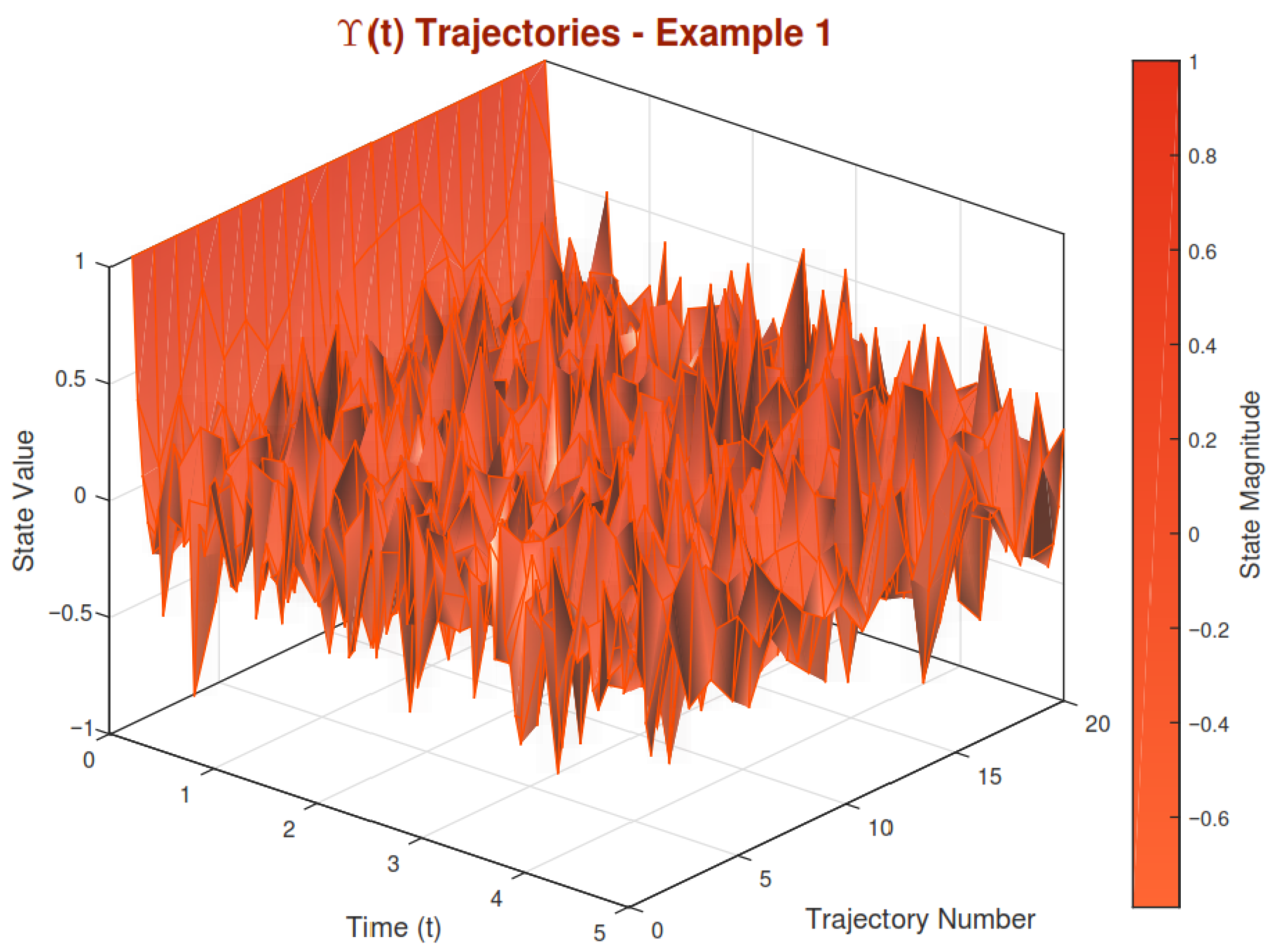
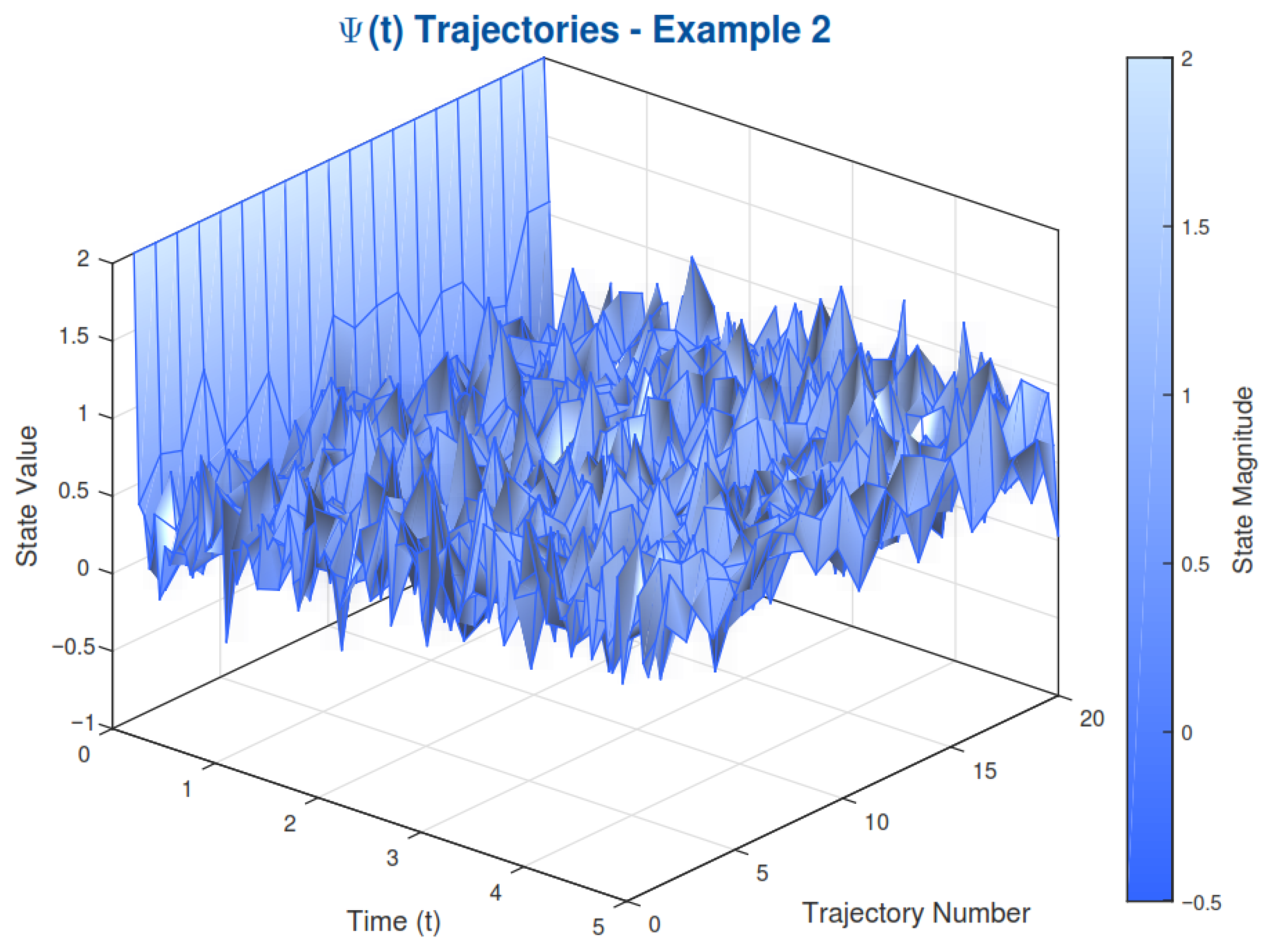
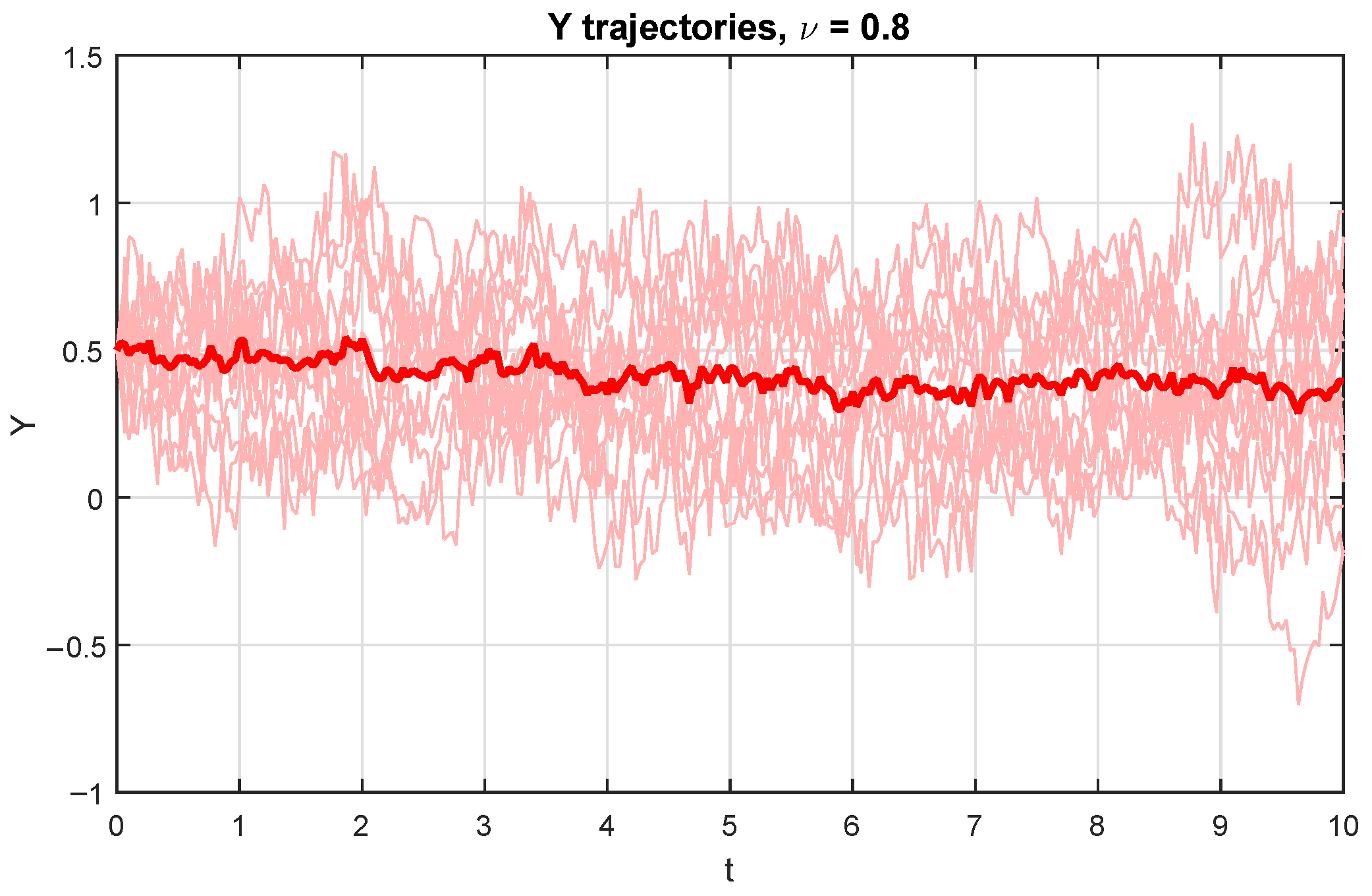
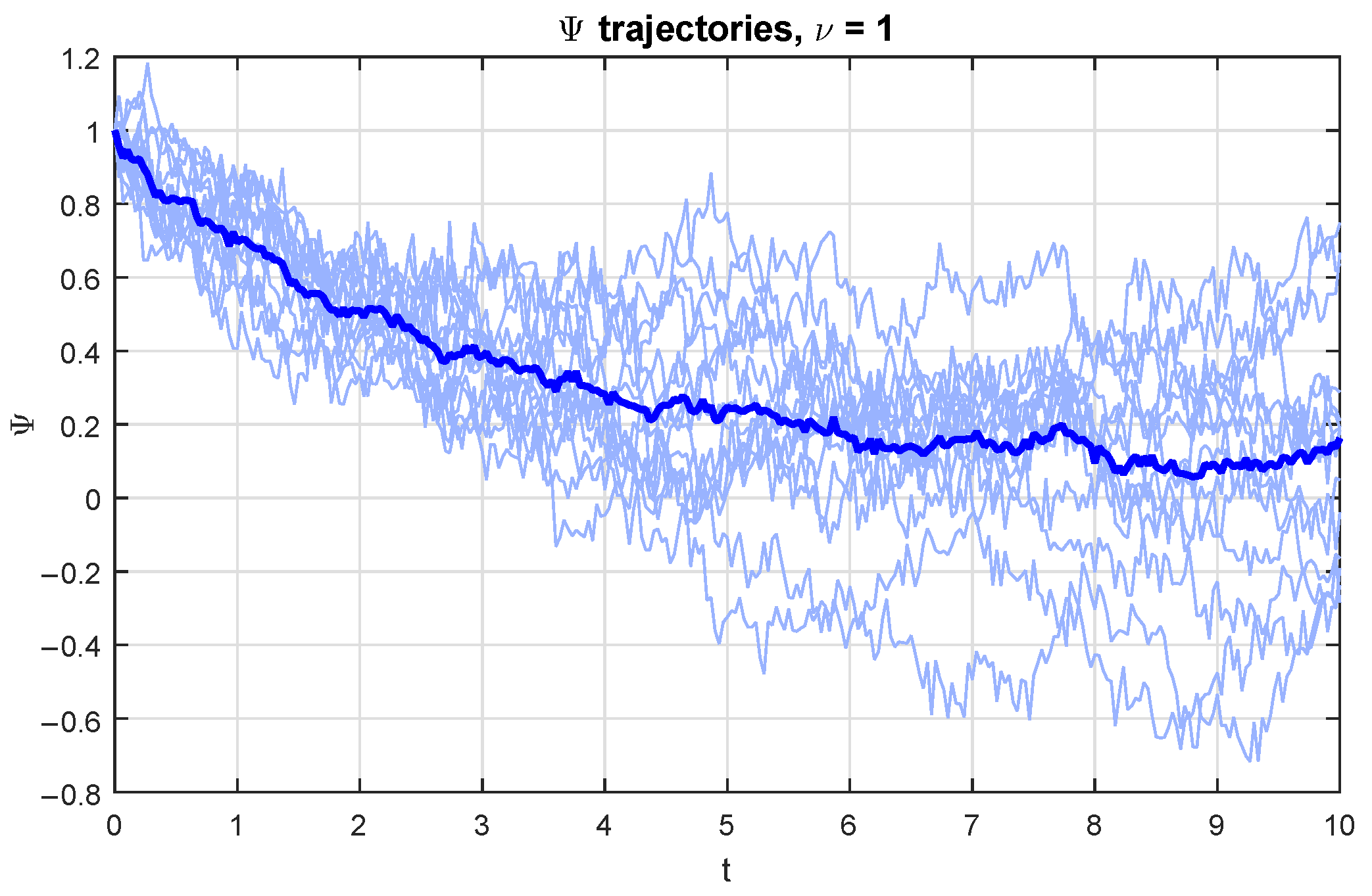
5. Examples
6. Numerical Scheme: Adams–Bashforth Method for the ABC System
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations:Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Hamza, A.E.; Osman, O.; Ali, A.; Alsulami, A.; Aldwoah, K.; Mustafa, A.; Saber, H. Fractal-fractional-order modeling of liver fibrosis disease and its mathematical results with subinterval transitions. Fractal Fract. 2024, 8, 638. [Google Scholar] [CrossRef]
- Saber, H.; Almalahi, M.A.; Albala, H.; Aldwoah, K.; Alsulami, A.; Shah, K.; Moumen, A. Investigating a nonlinear fractional evolution control model using W-piecewise hybrid derivatives: An application of a breast cancer model. Fractal Fract. 2024, 8, 735. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Jarad, F.; Uğurlu, E.; Abdeljawad, T.; Baleanu, D. On a new class of fractional operators. Adv. Differ. Equ. 2017, 2017, 247. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; World Scientific: Singapore, 2010. [Google Scholar]
- Øksendal, B. Stochastic Differential Equations: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Applications; Horwood Publishing: Chichester, UK, 2007. [Google Scholar]
- Allen, L.J.S. An Introduction to Stochastic Processes with Applications to Biology; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Alqahtani, A.M.; Akram, S.; Ahmad, J.; Aldwoah, K.A.; Rahman, M.U. Stochastic wave solutions of fractional Radhakrishnan–Kundu–Lakshmanan equation arising in optical fibers with their sensitivity analysis. J. Opt. 2024. [Google Scholar] [CrossRef]
- Lu, W.; Ahmad, J.; Akram, S.; Aldwoah, K.A. Soliton solutions and sensitive analysis to nonlinear wave model arising in optics. Phys. Scr. 2024, 99, 085230. [Google Scholar] [CrossRef]
- Hale, J.K.; Verduyn Lunel, S.M. Dynamics and Delays; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Lu, W.; Chen, G.; Cheng, D. Synchronization of coupled chaotic oscillators with time-varying delay. Chaos Solitons Fractals 2002, 14, 883–893. [Google Scholar]
- Liberzon, D. Switching in Systems and Control; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Hale, J.K.; Verduyn Lunel, S.M. Introduction to Functional Differential Equations; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Heemels, W.P.M.H.; De Schutter, B.; Van den Bosch, P.P.J. Hybrid dynamical systems: Modeling, stability, and robustness. Control Eng. Pract. 2009, 17, 1079–1087. [Google Scholar]
- Van der Schaft, A.; Schumacher, H. Introduction to Hybrid System Modeling and Control; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Mao, X.; Yuan, C.G. Stochastic Differential Equations with Markovian Switching; Imperial College Press: London, UK, 1997. [Google Scholar]
- Yan, Y.; Zhang, H.; Sun, J.; Wang, Y. Sliding mode control based on reinforcement learning for TS fuzzy fractional-order multiagent system with time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 10368–10379. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Erickson, A.M.; Henry, B.I.; McGann, A.V.; Murray, J.M.; Nichols, J.A. Fractional-Order Compartment Models for Epidemic Spread. SIAM J. Appl. Math. 2017, 77, 430–446. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Chen, P.; Wang, B.; Tian, Y.; Yang, Y. Finite-time stability of a time-delay fractional-order hydraulic turbine regulating system. IEEE Access. 2019, 7, 82613–82623. [Google Scholar] [CrossRef]
- Dong, J.; Yang, Y. Hybrid Switching in Fractional-Order Neural Networks. Neural Netw. 2021, 133. [Google Scholar]
- Zhang, S.; Yu, Y.; Wang, H. Mittag-Leffler stability of fractional-order Hopfield neural networks. Nonlinear Analysis: Hybrid Systems. 2015, 16, 104–121. [Google Scholar] [CrossRef]
- Arnold, L. Stochastic Differential Equations: Theory and Applications; Wiley: Hoboken, NJ, USA, 1974. [Google Scholar]
- Yin, G.G.; Zhang, Q. Discrete-Time Markov Chains and Applications; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Kushner, H.J. Stochastic Stability and Control; Academic Press: Cambridge, MA, USA, 1967. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Saddle River, NJ, USA, 2002. [Google Scholar]
- Banks, H.T.; Burns, J.A. Hereditary Control Problems: Numerical Methods Based on Averaging Approximations. SIAM J. Control Optim. 2006, 16, 169–208. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Prato, G.D.; Zabczyk, J. Stochastic Equations in Infinite Dimensions; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Mahmudov, N.I. Existence and uniqueness results for neutral SDEs in hilbert spaces. Stoch. Anal. Appl. 2007, 24, 79–95. [Google Scholar] [CrossRef]
- Govindan, T.E. Stability of mild solutions of stochastic evolution equations with variable delay. Stoch. Anal. Appl. 2003, 21, 1059–1077. [Google Scholar] [CrossRef]
- Taniguchi, T. Successive approximations to solutions of stochastic differential equations. J. Differ. Equ. 1992, 96, 152–169. [Google Scholar] [CrossRef]
- Yamada, T. On the successive approximation of solutions of stochastic differen- tial equations. J. Math. 1981, 21, 501–515. [Google Scholar]
- Rodkina, A.E. On existence and uniqueness of solution of stochastic differential equations with heredity. Stochastics 1984, 12, 187–200. [Google Scholar] [CrossRef]
- Balasubramaniam, P.; Vinayagam, D. Existence of solutions of nonlinear neu- tral stochastic differential inclusions in a hilbert space. Stoch. Anal. Appl. 2006, 23, 137–151. [Google Scholar] [CrossRef]
- Jiang, F.; Shen, Y. A note on the existence and uniqueness of mild solutions to neutral stochastic partial differential equations with non-Lipschitz coefficients. Comput. Math. Appl. 2011, 61, 1590–1594. [Google Scholar] [CrossRef]
- Govindan, T.E. Almost sure exponential stability for stochastic neutral partial functional differential equations. Stochastics 2005, 77, 139–154. [Google Scholar] [CrossRef]
- Ahmadova, A.; Mahmudov, N.I. Existence and uniqueness results for a class of fractional stochastic neutral differential equations. Chaos Solitons Fractals 2020, 139, 110253. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J.F. Decolonisation of fractional calculus rules: Breaking commutativity and associativity to capture more natural phenomena. Eur. Phys. J. Plus 2018, 133, 166. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Alghamdi, M.A.; El-Sayed, A.M.A.; El-Sayed, A.M.A. Mean-square stability of Riemann–Liouville fractional Hopfield’s neural networks with impulses at random times. Adv. Differ. Equ. 2021, 2021, 237. [Google Scholar] [CrossRef]
- Belhenniche, A.; Guran, L.; Benahmed, S.; Lobo Pereira, F. Solving nonlinear and dynamic programming equations on extended b-metric spaces with the fixed-point technique. Fixed Point Theory Algorithms Sci. Eng. 2022, 2022, 24. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sidaoui, R.; Alfedeel, A.H.A.; Ahmad, J.; Aldwoah, K.; Ali, A.; Osman, O.; Tedjani, A.H. Mathematical Perspectives of a Coupled System of Nonlinear Hybrid Stochastic Fractional Differential Equations. Fractal Fract. 2025, 9, 622. https://doi.org/10.3390/fractalfract9100622
Sidaoui R, Alfedeel AHA, Ahmad J, Aldwoah K, Ali A, Osman O, Tedjani AH. Mathematical Perspectives of a Coupled System of Nonlinear Hybrid Stochastic Fractional Differential Equations. Fractal and Fractional. 2025; 9(10):622. https://doi.org/10.3390/fractalfract9100622
Chicago/Turabian StyleSidaoui, Rabeb, Alnadhief H. A. Alfedeel, Jalil Ahmad, Khaled Aldwoah, Amjad Ali, Osman Osman, and Ali H. Tedjani. 2025. "Mathematical Perspectives of a Coupled System of Nonlinear Hybrid Stochastic Fractional Differential Equations" Fractal and Fractional 9, no. 10: 622. https://doi.org/10.3390/fractalfract9100622
APA StyleSidaoui, R., Alfedeel, A. H. A., Ahmad, J., Aldwoah, K., Ali, A., Osman, O., & Tedjani, A. H. (2025). Mathematical Perspectives of a Coupled System of Nonlinear Hybrid Stochastic Fractional Differential Equations. Fractal and Fractional, 9(10), 622. https://doi.org/10.3390/fractalfract9100622







