Analysis of Vehicle Vibration Considering Fractional Damping in Suspensions and Tires
Abstract
1. Introduction
2. Fractional Damping Element
2.1. Theory of Fractional Calculus
- (1)
- Linear property
- (2)
- Laplace transforms property
2.2. Fractional Damping Elements
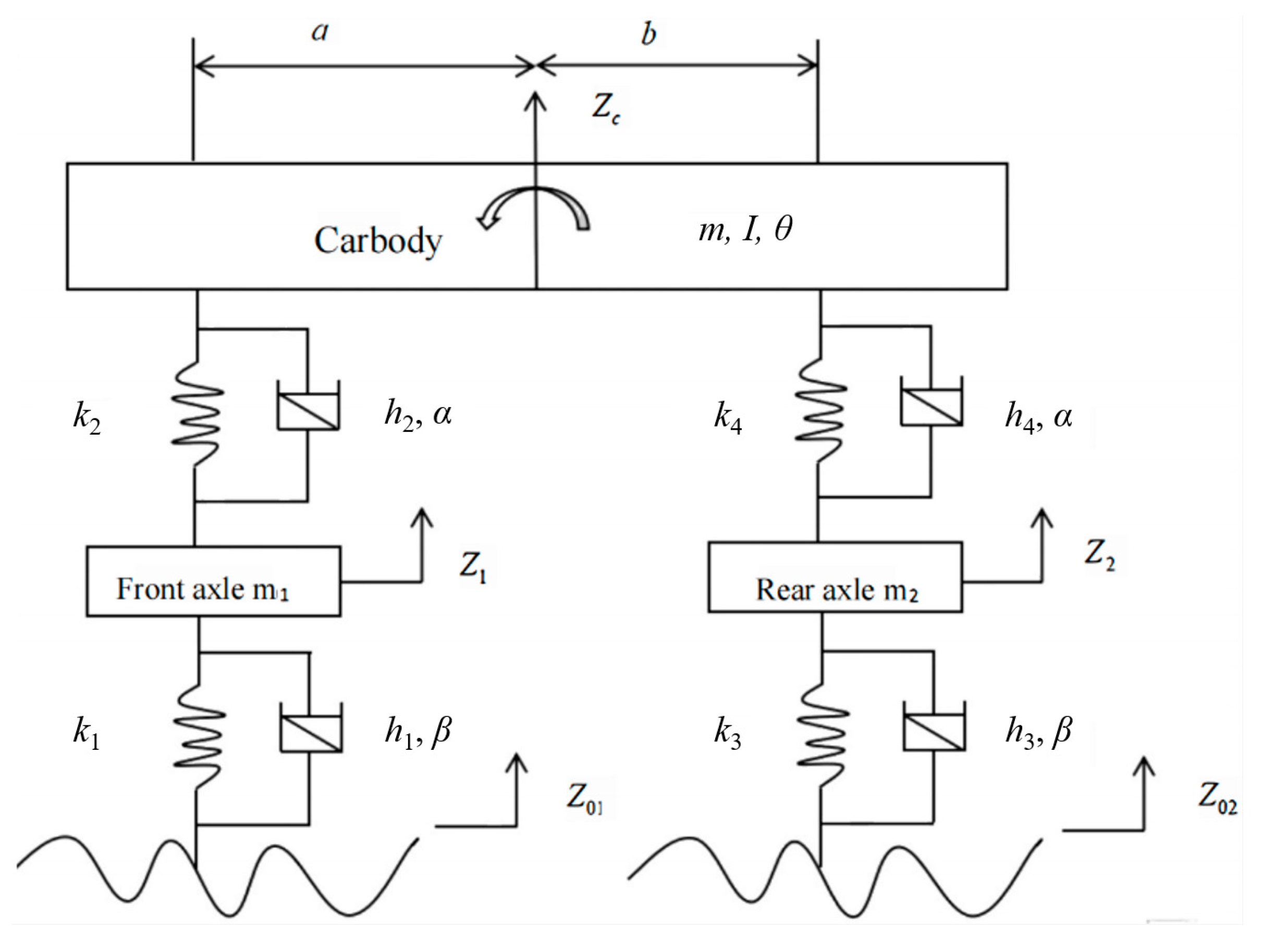
3. Modeling of Car Dynamics Based on Fractional Damping
3.1. Simplification of the Whole Car Dynamics Modeling
3.2. Modeling of Pavement Irregularities’ Excitation Signals
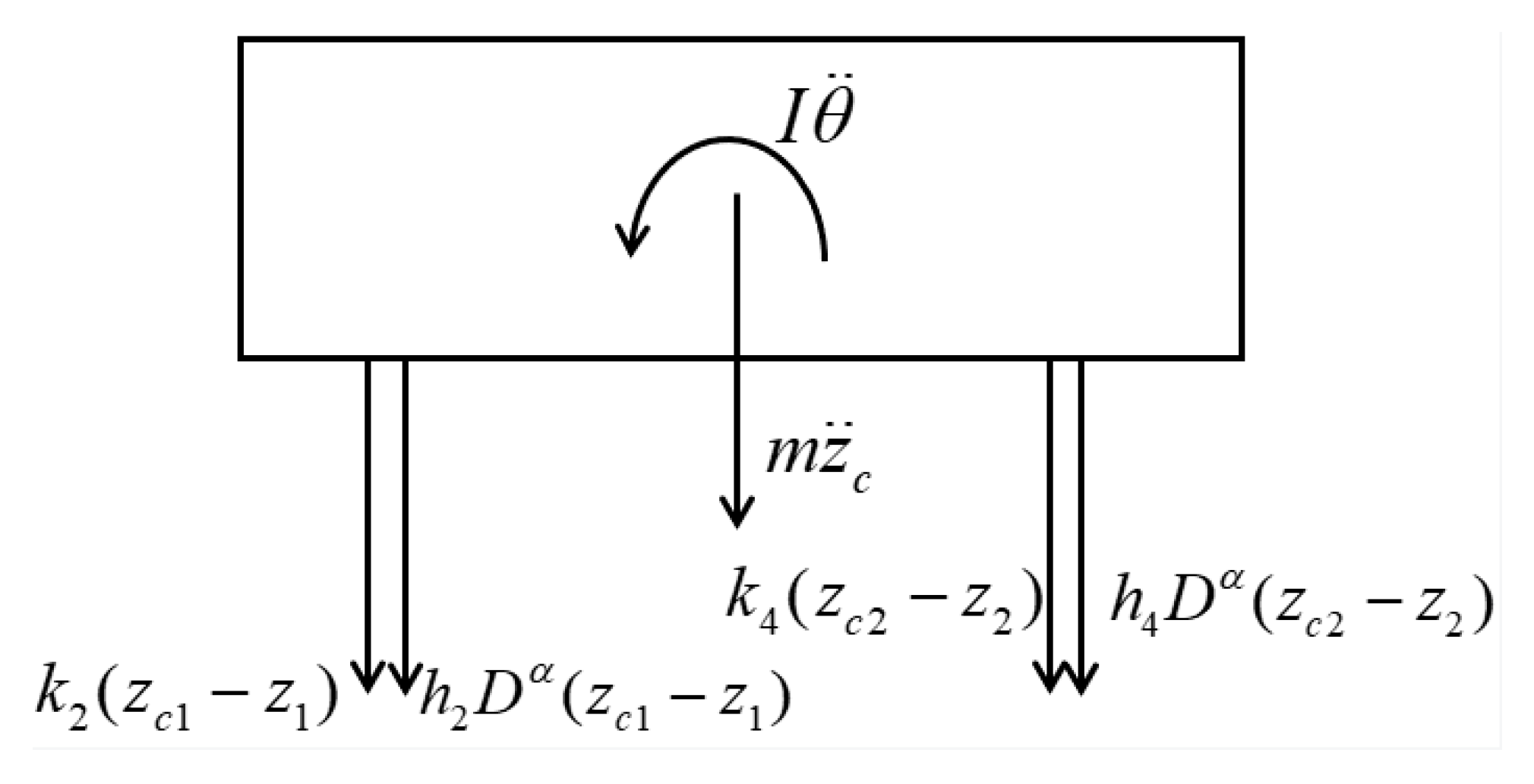
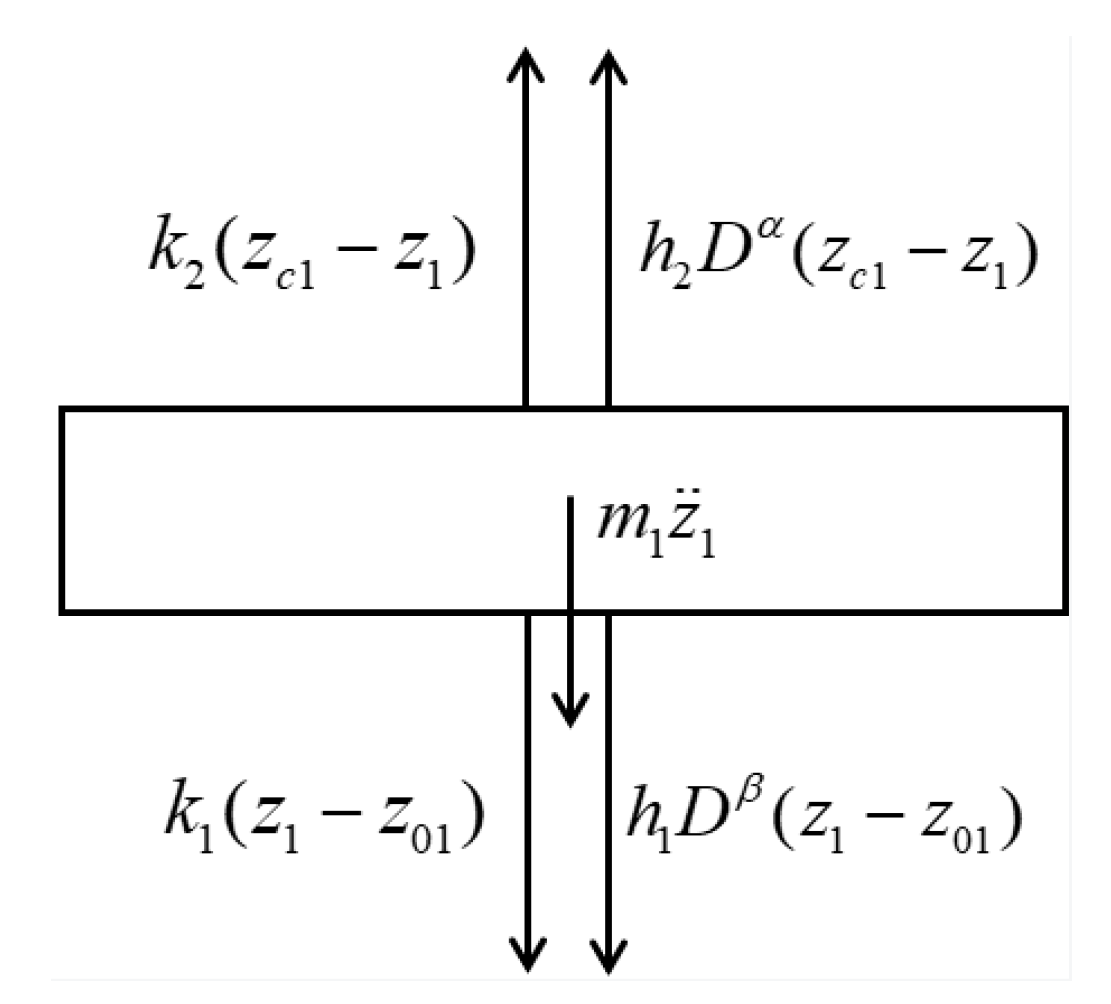
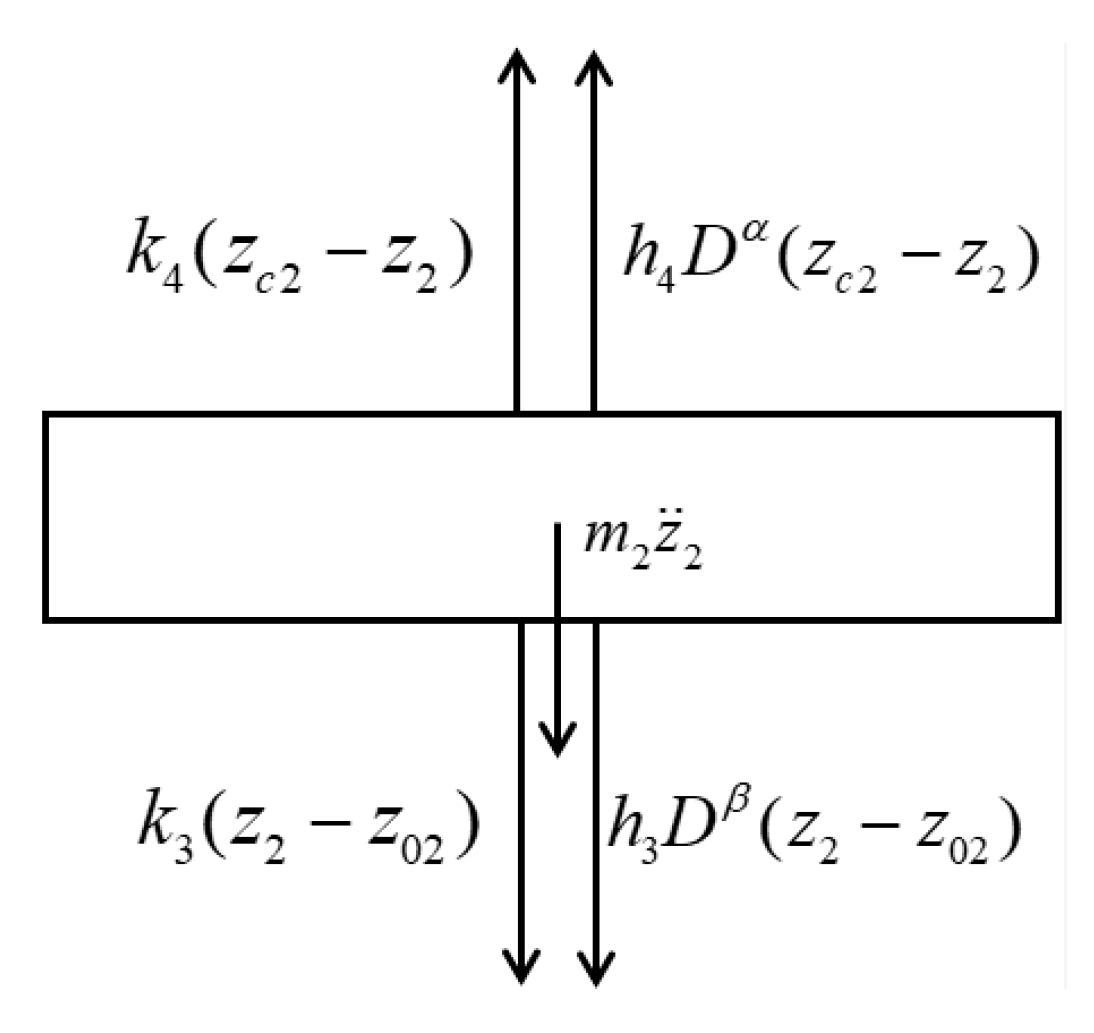
3.3. Derivation of Dynamical Equations with Fractional Damping Element
3.4. Transfer Function Representation of Vibration Response
3.5. Validation for Transfer Function Method
4. Results and Discussions
4.1. Effect of Suspensions on Car Vibration
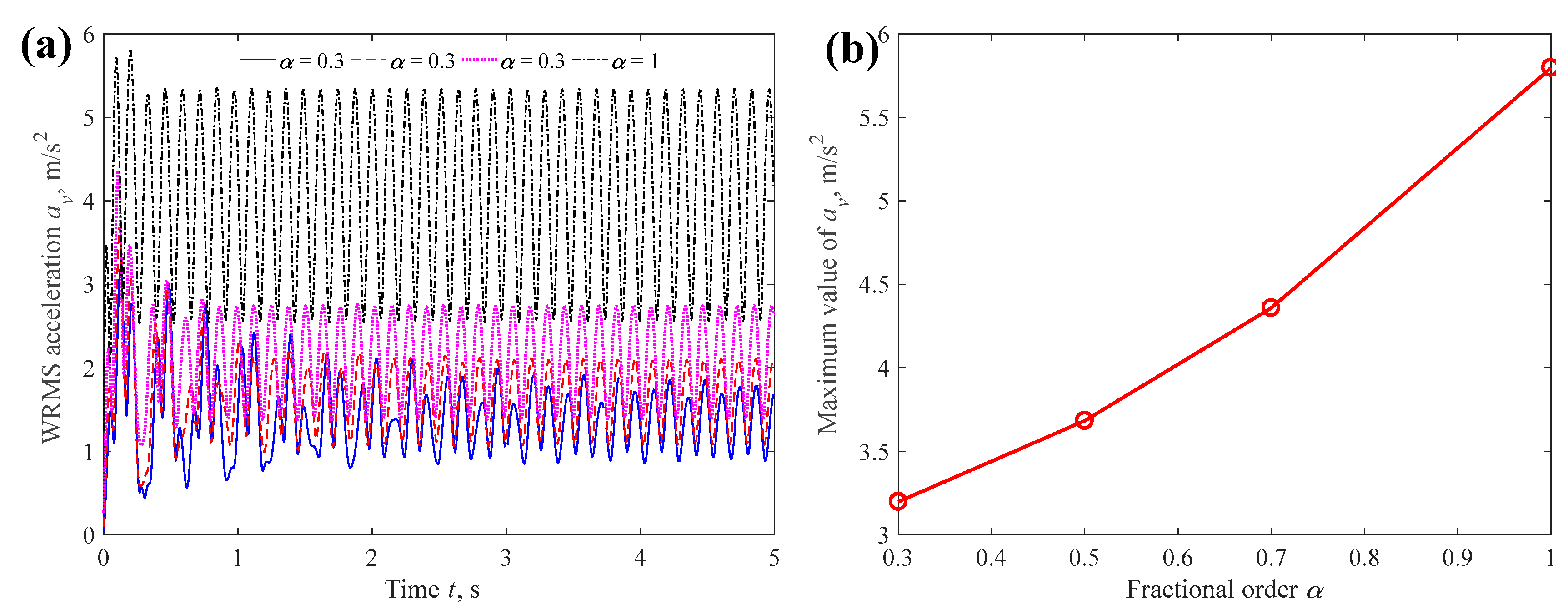
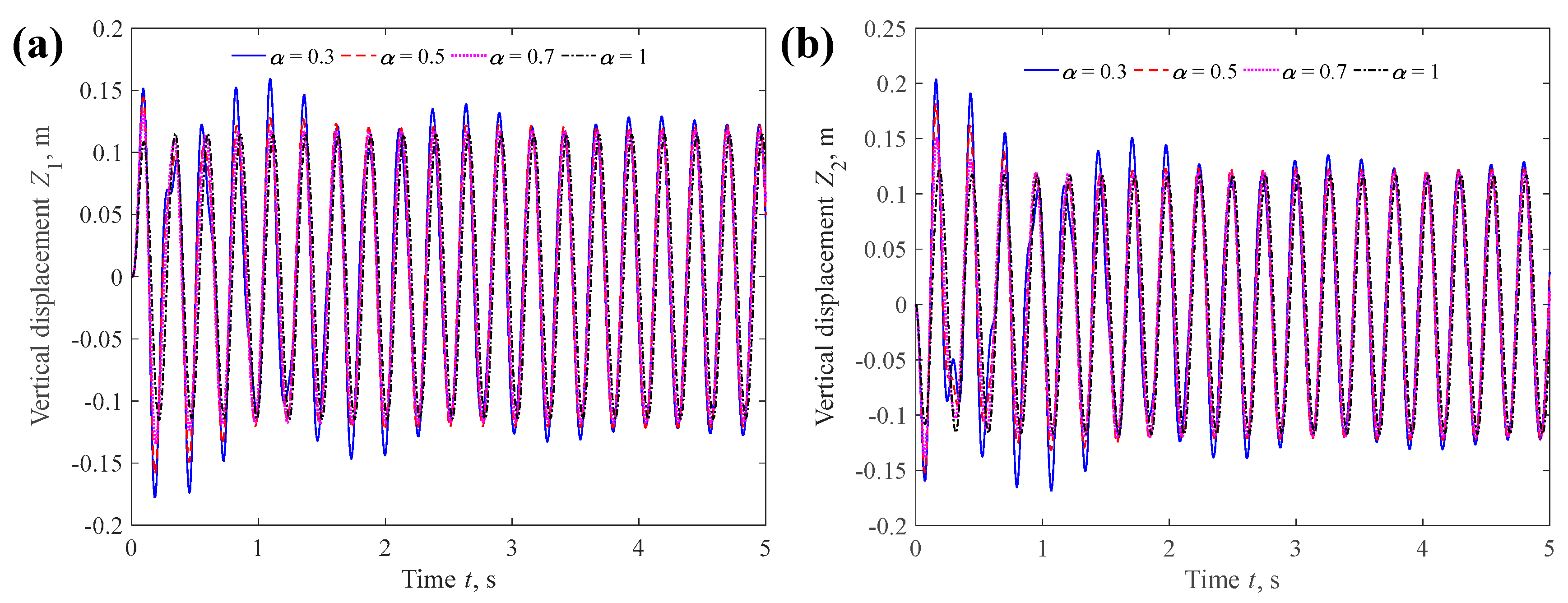
4.1.1. Fractional Order α
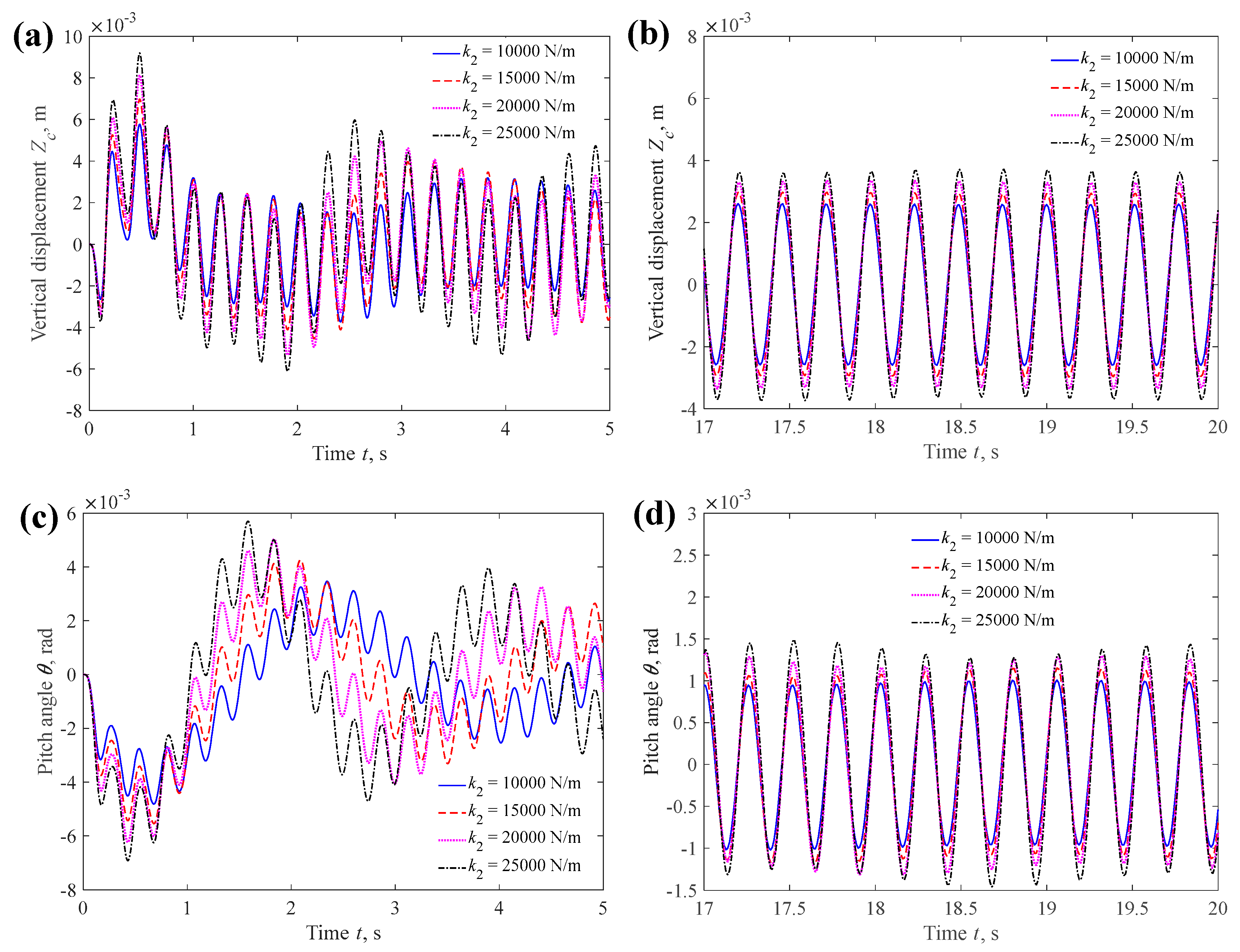
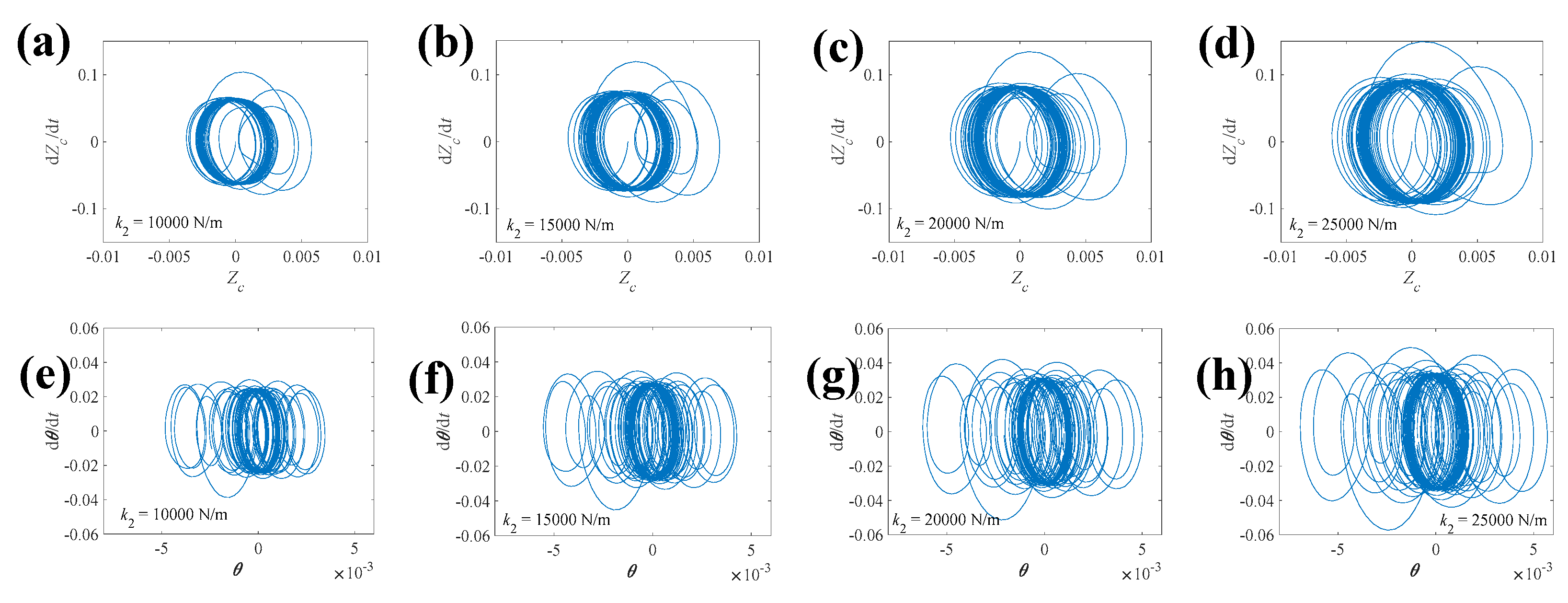
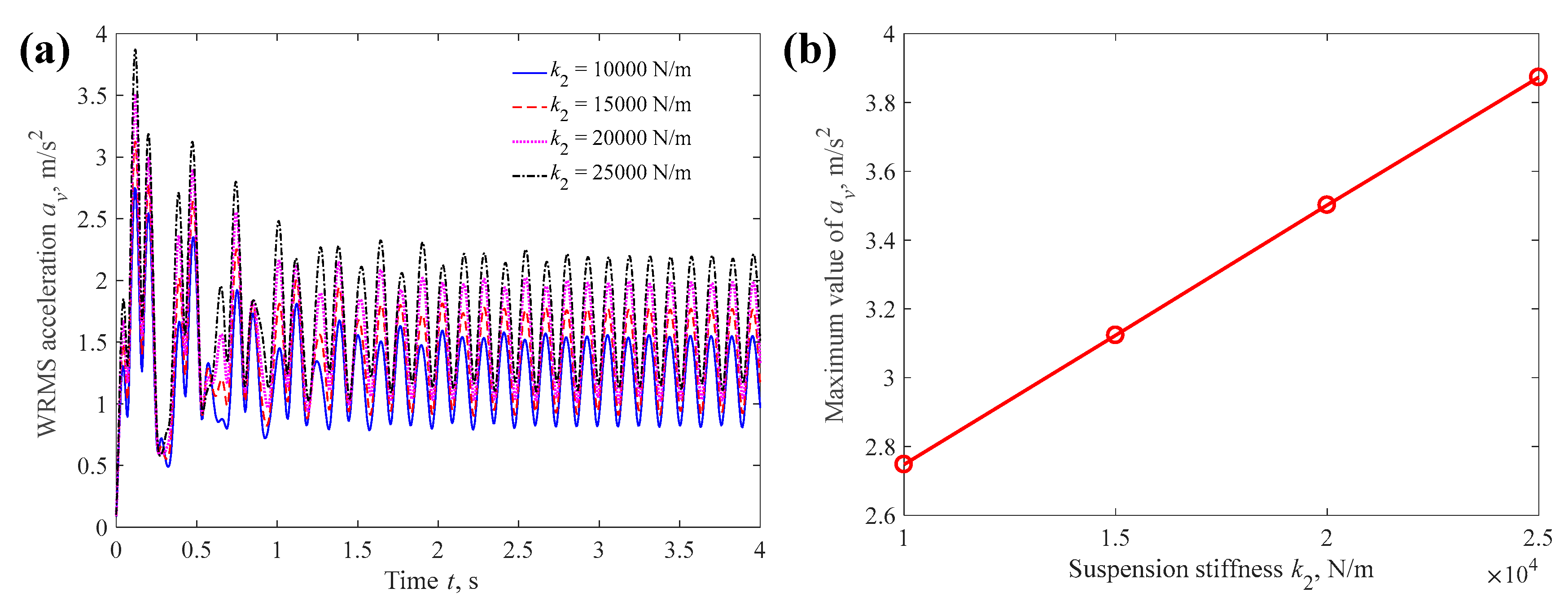
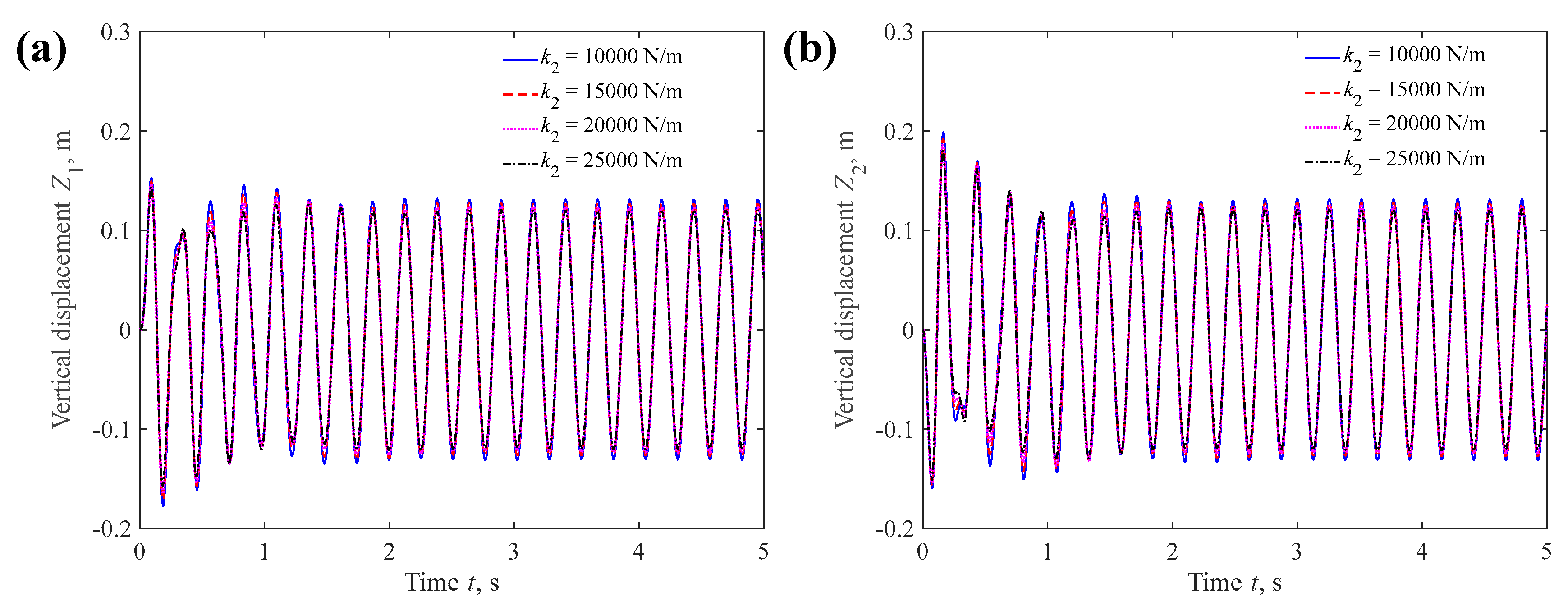
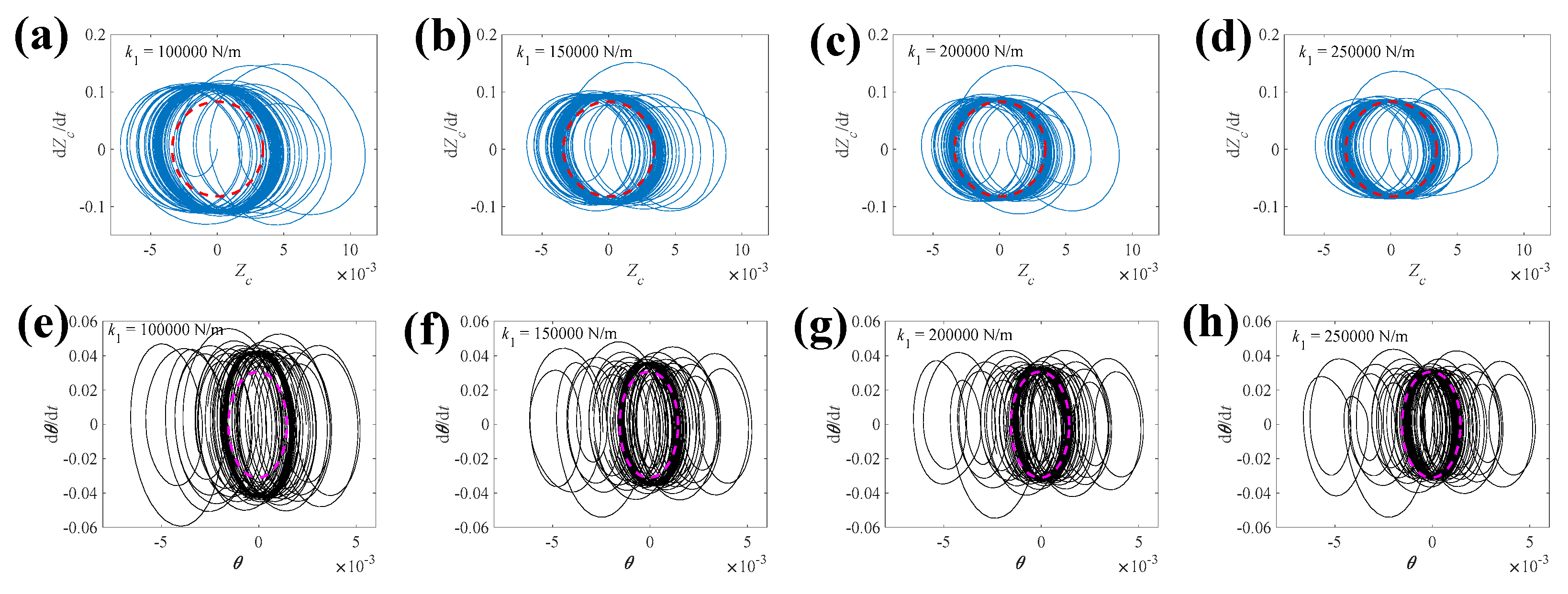
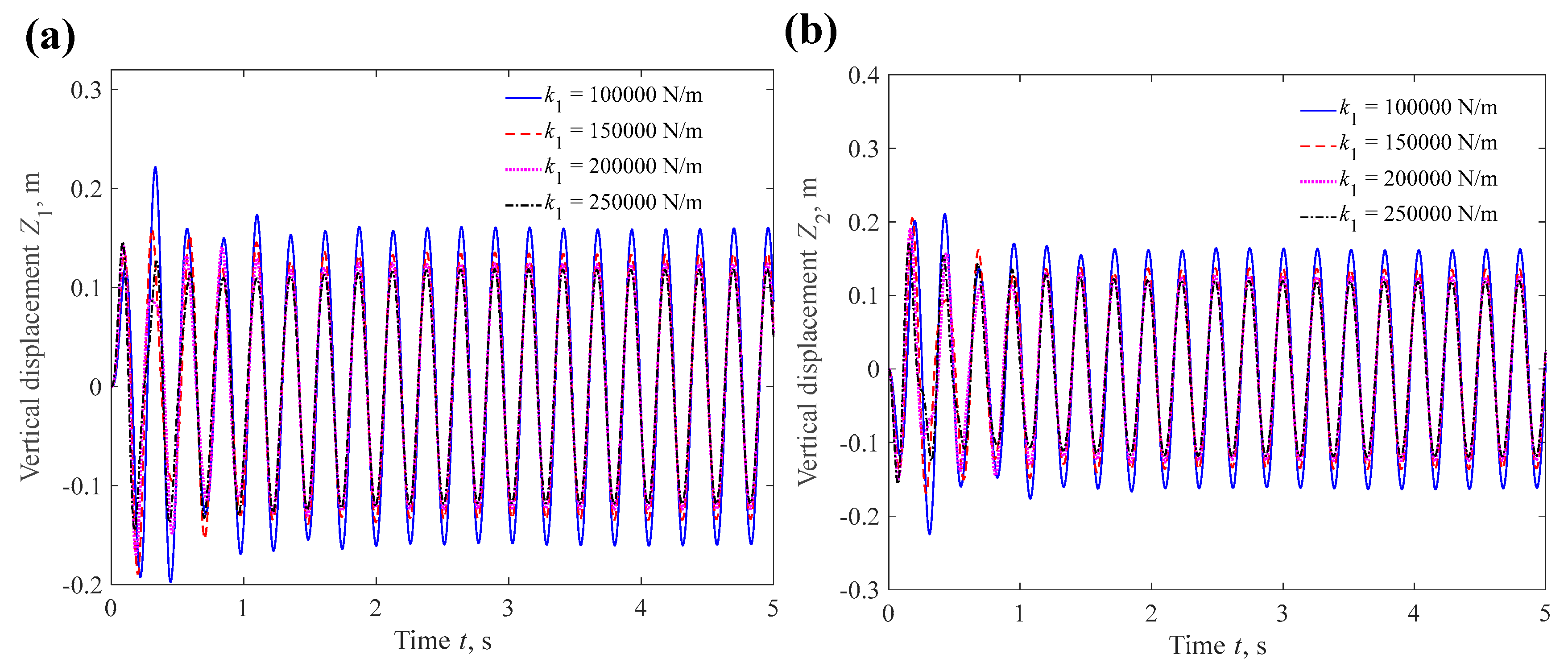
4.1.2. Suspension Stiffness
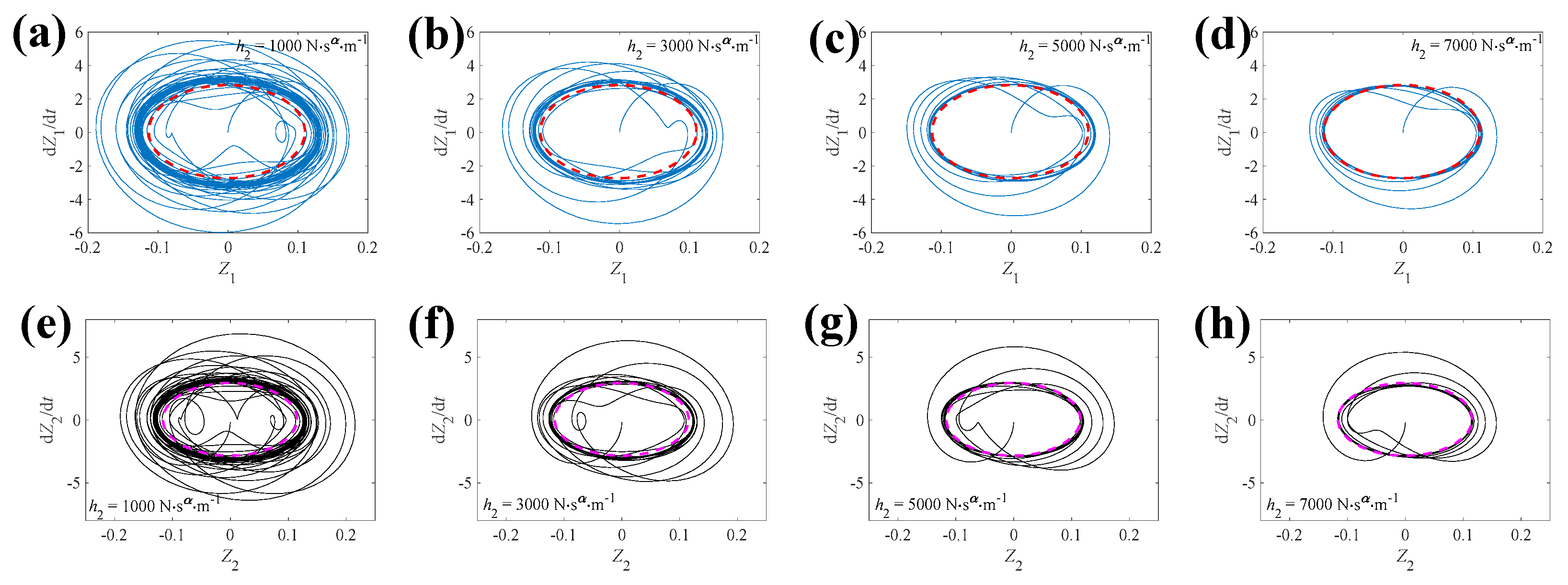
4.1.3. Suspension Damping
4.2. Effect of Tires on Car Vibration
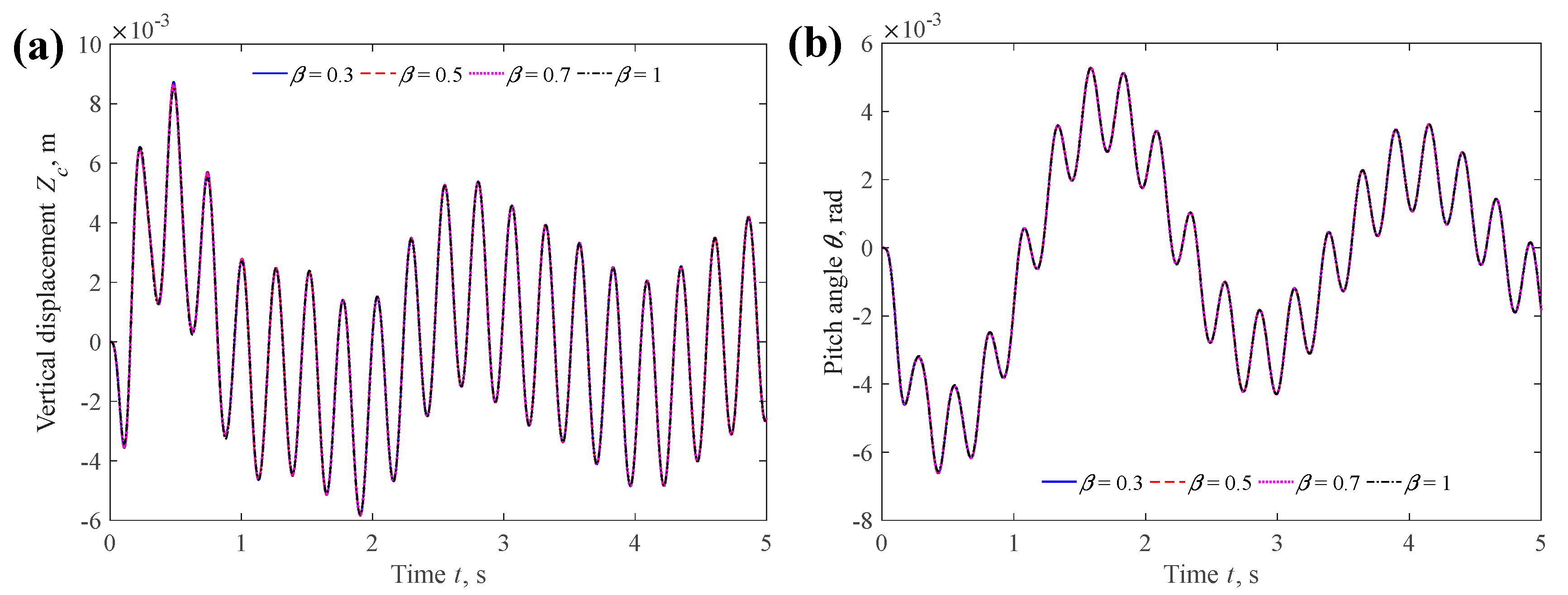
4.2.1. Fractional Order β
4.2.2. Tire Stiffness
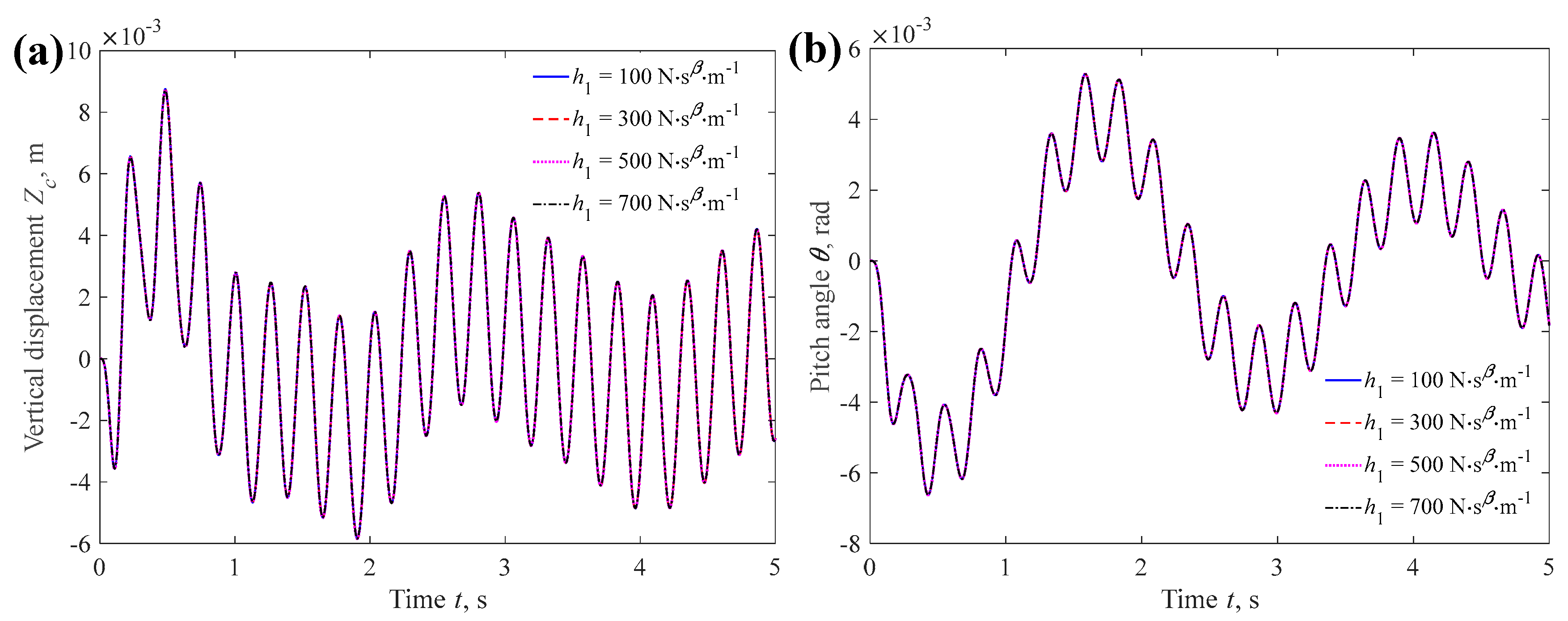
4.2.3. Tire Damping
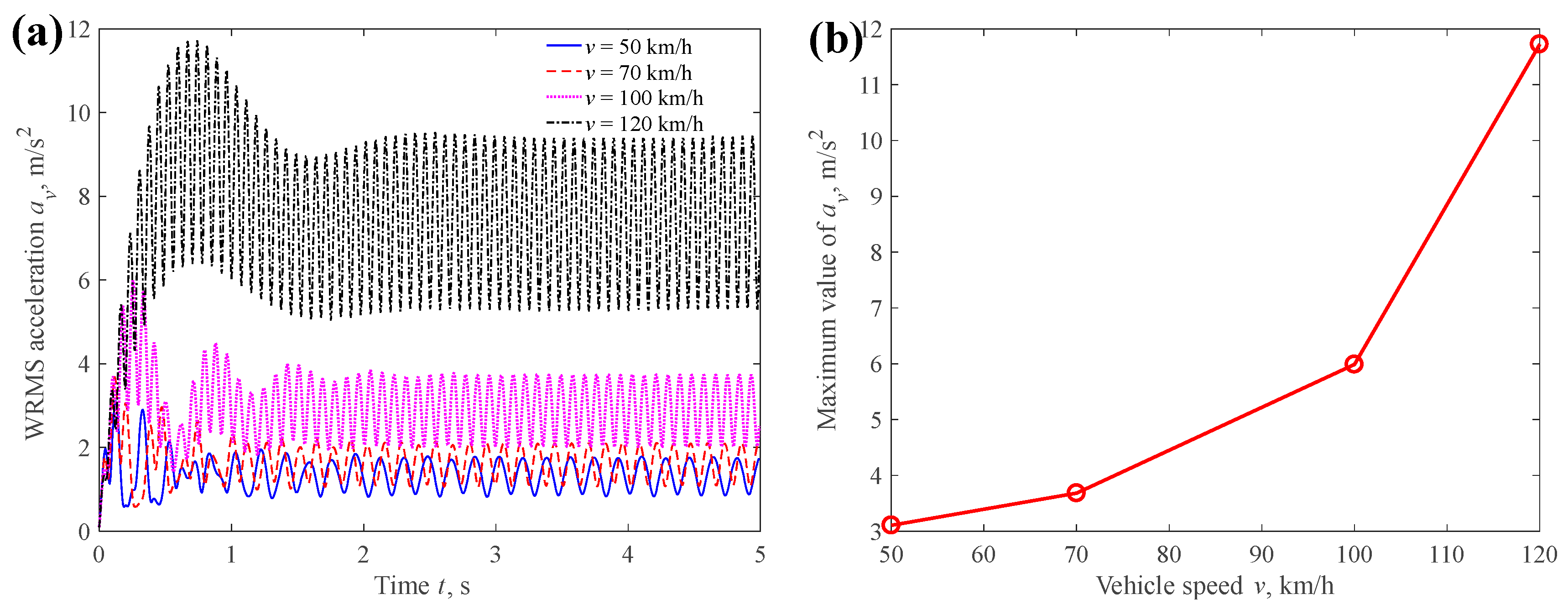
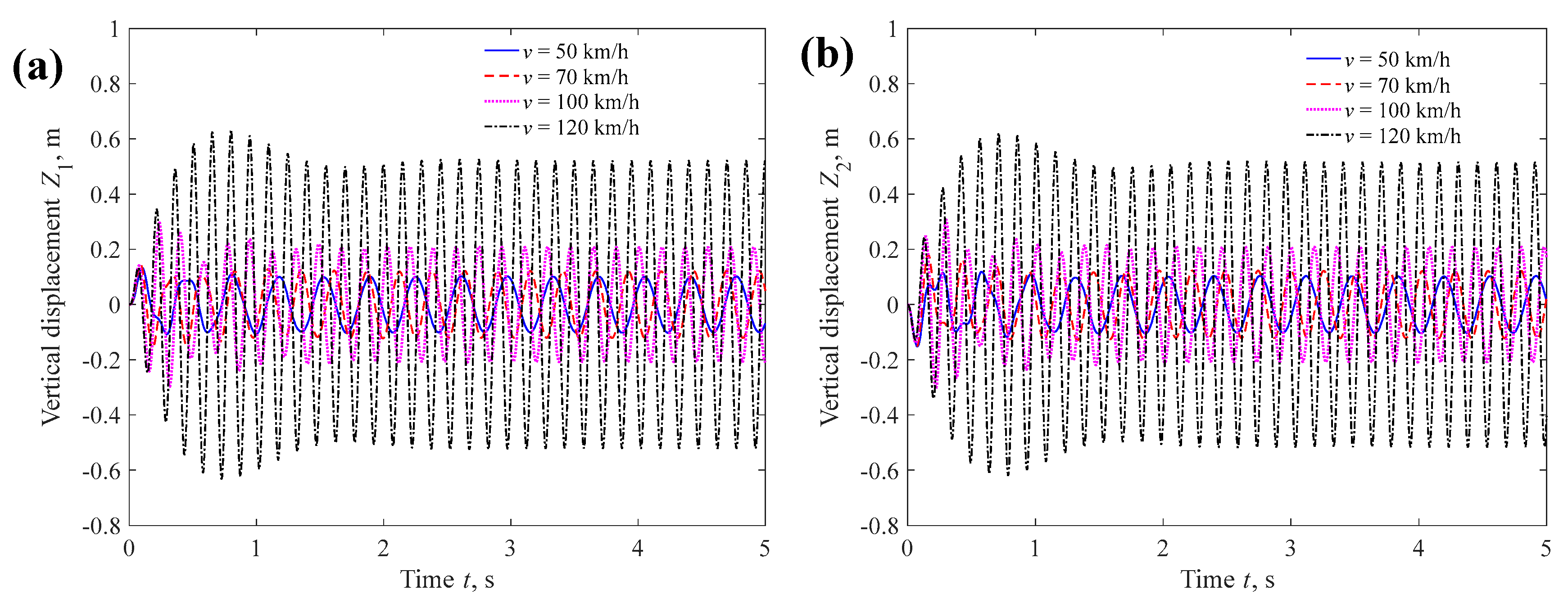
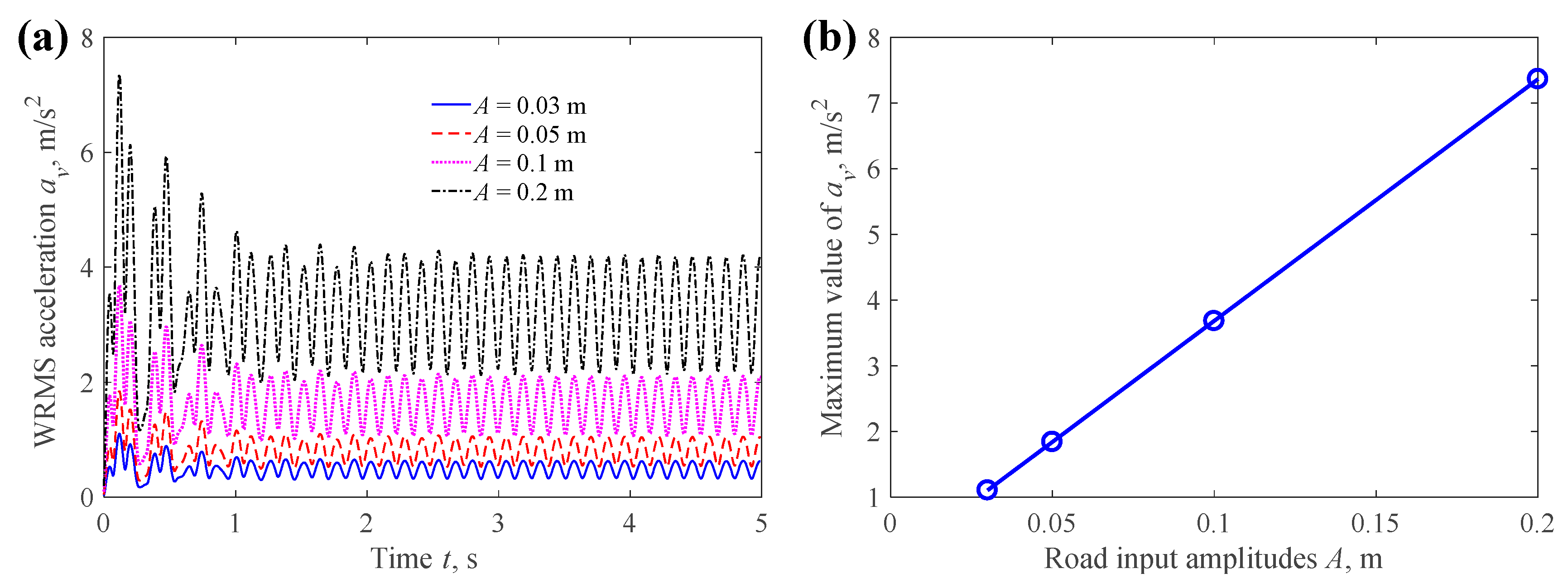
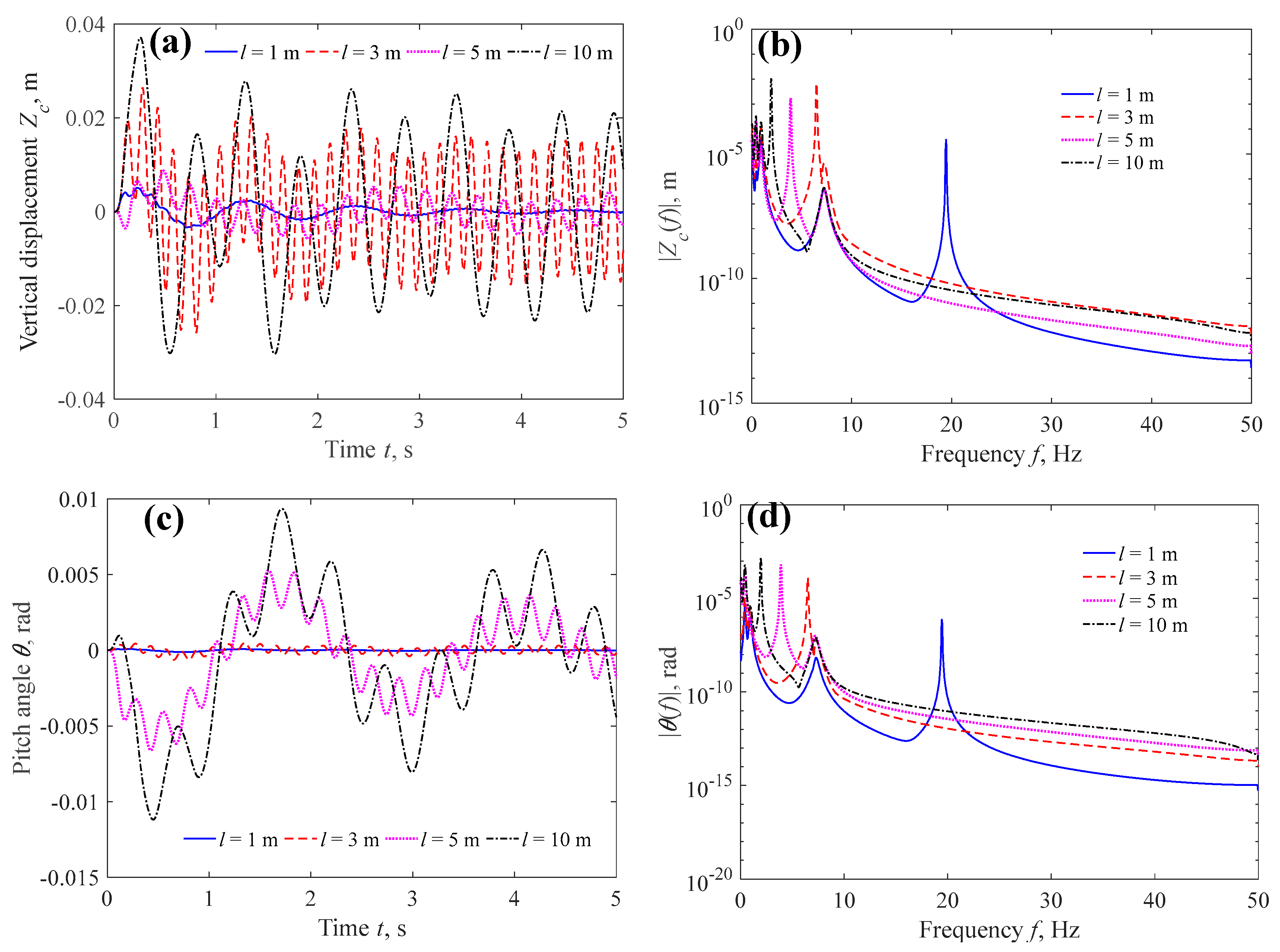
4.3. Effects of Pavement Excitation and Car Speed on Car Vibration
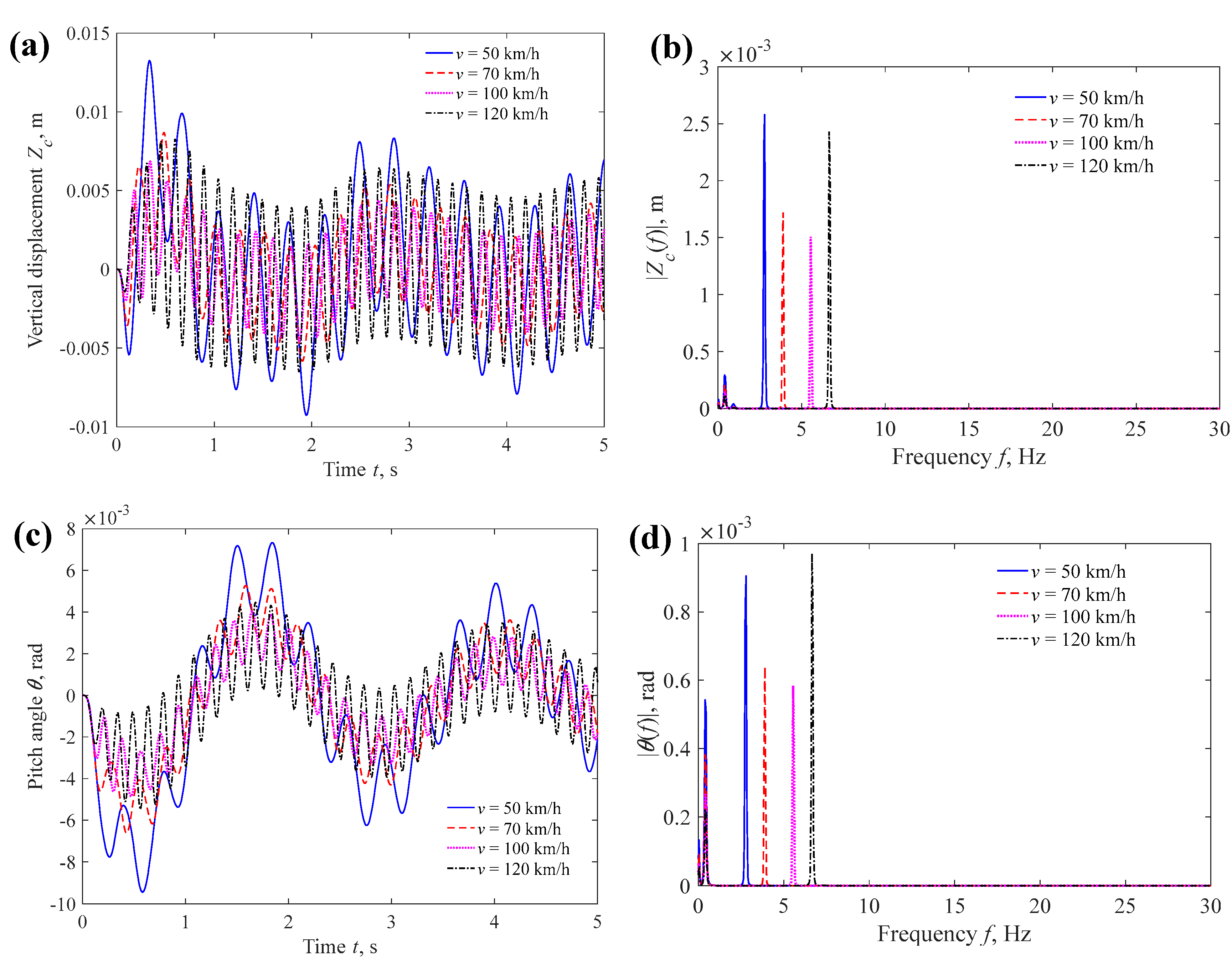
4.3.1. Car Speed
4.3.2. Pavement Input Amplitude
4.3.3. Pavement Input Length
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Attias, D. The Automobile Revolution; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Yang, S.; Lu, Y.; Li, S. An overview on vehicle dynamics. Int. J. Dyn. Control 2013, 1, 385–395. [Google Scholar] [CrossRef]
- Zhou, S.; Song, G.; Sun, M.; Ren, Z. Nonlinear dynamic analysis of a quarter vehicle system with external periodic excitation. Int. J. Nonlin. Mech. 2016, 84, 82–93. [Google Scholar] [CrossRef]
- Segel, L. An overview of developments in road vehicle dynamics: Past, present and future. In Proceedings of the IMechE Conference on Vehicle Ride and Handling, London, UK, 15–17 November 1993; pp. 1–12. [Google Scholar]
- Wang, X. Analysis and Research of Vibration Characteristics of Coach. Master’s Thesis, Hefei University of Technology, Hefei, China, 2010. [Google Scholar]
- Verros, G.; Natsiavas, S.; Papadimitriou, C. Design optimization of quarter-car models with passive and semi-active suspensions under random road excitation. J. Vib. Control 2005, 11, 581–606. [Google Scholar] [CrossRef]
- Borowiec, M.; Litak, G.; Friswell, M.I. Nonlinear response of an oscillator with a magneto-rheological damper subjected to external forcing. Appl. Mech. Mater. 2006, 5, 277–284. [Google Scholar] [CrossRef]
- Türkay, S.; Akçay, H. A study of random vibration characteristics of the quarter-car model. J. Sound Vib. 2005, 282, 111–124. [Google Scholar] [CrossRef]
- Liang, S.; Li, C.; Zhu, Q.; Xiong, Q. The influence of parameters of consecutive speed control humps. J. Vibroeng. 2011, 13, 406–413. [Google Scholar]
- Paliwal, V.; Dobriyal, R.; Kumar, P.; Manral, A.R. Effect of varying road profile amplitude on the behavior of a nonlinear quarter car model. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1149, 012015. [Google Scholar] [CrossRef]
- Yang, Z.; Liang, S.; Zhu, Q.; Sun, Y.; Zhan, S. Chaotic Vibration and Comfort Analysis of Nonlinear Half-Vehicle Mode Excited by Consecutive Speed-Control Humps. J. Robot. Mechatron. 2015, 27, 513–519. [Google Scholar] [CrossRef]
- Zhu, Q.; Ishitobi, M. Chaos and bifurcations in a nonlinear vehicle model. J. Sound Vib. 2004, 275, 1136–1146. [Google Scholar] [CrossRef]
- Zhu, Q.; Ishitobi, M. Chaotic vibration of a nonlinear full-vehicle model. Int. J. Solids Struct. 2006, 43, 747–759. [Google Scholar] [CrossRef]
- Cebon, D. Handbook of Vehicle-Road Interaction; Swets & Zeitlinger: Lisse, The Netherlands, 1999. [Google Scholar]
- Yang, S.; Chen, L.; Li, S. Dynamics of Vehicle-Road Coupled System; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Li, S.; Yang, S.; Guo, W. Investigation on chaotic motion in hysteretic non-linear suspension system with multi-frequency excitations. Mech. Res. Commun. 2004, 31, 229–236. [Google Scholar] [CrossRef]
- Dobriyal, R.; Kumar, P.; Jha, N.K.; Paliwal, V.; Gariya, N. Dynamics and optimization of a quarter car model with power law spring. AIP Conf. Proc. 2023, 2521, 020016. [Google Scholar] [CrossRef]
- Abolfathi, A. Can a nonlinear quasi-zero-stiffness spring improve the ride quality of a vehicle? Veh. Syst. Dyn. 2024, 62, 330–346. [Google Scholar] [CrossRef]
- Chen, H.; Chen, G.; Meng, Z.; Yang, D. Stochastic bifurcation and dynamic reliability analyses of nonlinear MDOF vehicle system with generalized fractional damping via DPIM. Nonlinear Dynam. 2024, 112, 5291–5316. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Singapore, 2010. [Google Scholar]
- Su, X.; Yao, D.; Xu, W. Processing of viscoelastic data via a generalized fractional model. Int. J. Eng. Sci. 2021, 161, 103465. [Google Scholar] [CrossRef]
- Su, X.; Yao, D.; Xu, W. A new method for formulating linear viscoelastic models. Int. J. Eng. Sci. 2020, 156, 103375. [Google Scholar] [CrossRef]
- Cai, W.; Wang, P. Fractional modeling of temperature-dependent mechanical behaviors for glassy polymers. Int. J. Mech. Sci. 2022, 232, 107607. [Google Scholar] [CrossRef]
- Ullah, M.Z.; Mallawi, F.; Baleanu, D.; Alshomrani, A.S. A new fractional study on the chaotic vibration and state-feedback control of a nonlinear suspension system. Chaos Soliton. Fract. 2020, 132, 109530. [Google Scholar] [CrossRef]
- Nwagoum Tuwa, P.R.; Molla, T.; Noubissie, S.; Kingni, S.T.; Rajagopal, K. Analysis of a quarter car suspension based on a Kelvin–Voigt viscoelastic model with fractional-order derivative. Int. J. Nonlin. Mech. 2021, 137, 103818. [Google Scholar] [CrossRef]
- Chang, Y.; Zhu, Y.; Li, Y.; Wang, M. Dynamical analysis of a fractional-order nonlinear two-degree-of-freedom vehicle system by incremental harmonic balance method. J. Low Freq. Noise Vib. Act. Control 2024, 43, 706–728. [Google Scholar] [CrossRef]
- Watanabe, M.; Prasad, A. Fractional delayed feedback for semi-active suspension control of nonlinear jumping quarter car model. Chaos Soliton. Fract. 2025, 199, 116973. [Google Scholar] [CrossRef]
- Molla, T.; Duraisamy, P.; Rajagopal, K.; Karthikeyan, A.; Boulaaras, S. Exploring nonlinearity in quarter car models with an experimental approach to formulating fractional order form and its dynamic analysis. Sci. Rep. 2024, 14, 12074. [Google Scholar] [CrossRef]
- Yuvapriya, T.; Lakshmi, P.; Rajendiran, S. Vibration suppression in full car active suspension system using fractional order sliding mode controller. J. Braz. Soc. Mech. Sci. 2018, 40, 217. [Google Scholar] [CrossRef]
- He, R.; Zhao, B.; Dong, H. Analysis of automobile vibration response based on MATLAB. Auto. Appl. Technol. 2018, 20, 68–70. (In Chinese) [Google Scholar] [CrossRef]
- Brancik, L. Programs for fast numerical inversion of Laplace transforms in MATLAB language environment. In Proceedings of the 7th Conference MATLAB, Prague, Czech Republic, 21 October 1999; pp. 27–39. [Google Scholar]
- Gao, S.; Shen, H. Vibration Mechanics; China Railway Press: Beijing, China, 2016. [Google Scholar]
- Wang, C. Vechicle-Pavement Coupled Vibration Response for Unmanned Driving. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2022. [Google Scholar]















| Parameters | Physical Meaning | Unit | Values [30] |
|---|---|---|---|
| m | Car body mass | kg | 1535 |
| I | Vehicle body moment of inertia about the center of mass | kg·m2 | 17,577 |
| m1 | Front axle mass | kg | 128 |
| m2 | Rear axle mass | kg | 128 |
| k1 | Front tire stiffness | N·m−1 | 220,000 |
| k2 | Front suspension stiffness | N·m−1 | 22,741 |
| k3 | Rear tire stiffness | N·m−1 | 220,000 |
| k4 | Rear suspension stiffness | N·m−1 | 22,741 |
| h1 | Front tire damping | N·sβ·m−1 | 400 |
| h2 | Front suspension damping | N·sα·m−1 | 3800 |
| h3 | Rear tire damping | N·sβ·m−1 | 400 |
| h4 | Rear suspension damping | N·sα·m−1 | 4000 |
| a | Distance from front axle to the center of mass | m | 1.300 |
| b | Distance from rear axle to the center of mass | m | 1.705 |
| α | Fractional order in suspensions | - | |
| β | Fractional order in tires | - | |
| zc | Vertical displacement of the car body | m | |
| z1/z2 | Axle vertical displacement | m | |
| z01/z02 | Pavement excitation input | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, X.; Xie, S.; Li, J. Analysis of Vehicle Vibration Considering Fractional Damping in Suspensions and Tires. Fractal Fract. 2025, 9, 620. https://doi.org/10.3390/fractalfract9100620
Su X, Xie S, Li J. Analysis of Vehicle Vibration Considering Fractional Damping in Suspensions and Tires. Fractal and Fractional. 2025; 9(10):620. https://doi.org/10.3390/fractalfract9100620
Chicago/Turabian StyleSu, Xianglong, Shuangning Xie, and Jipeng Li. 2025. "Analysis of Vehicle Vibration Considering Fractional Damping in Suspensions and Tires" Fractal and Fractional 9, no. 10: 620. https://doi.org/10.3390/fractalfract9100620
APA StyleSu, X., Xie, S., & Li, J. (2025). Analysis of Vehicle Vibration Considering Fractional Damping in Suspensions and Tires. Fractal and Fractional, 9(10), 620. https://doi.org/10.3390/fractalfract9100620





