Fractional-Order PID Control of Two-Wheeled Self-Balancing Robots via Multi-Strategy Beluga Whale Optimization

Abstract

In recent years, fractional-order controllers have garnered increasing attention due to their enhanced flexibility and superior dynamic performance in control system design. Among them, the fractional-order Proportional–Integral–Derivative (FOPID) controller offers two additional tunable parameters, $\lambda$ and $\mu$, expanding the design space and allowing for finer performance tuning. However, the increased parameter dimensionality poses significant challenges for optimisation. To address this, the present study investigates the application of FOPID controllers to a two-wheeled self-balancing robot (TWSBR), with controller parameters optimised using intelligent algorithms. A novel Multi-Strategy Improved Beluga Whale Optimization (MSBWO) algorithm is proposed, integrating chaotic mapping, elite pooling, adaptive Lévy flight, and a golden sine search mechanism to enhance global convergence and local search capability. Comparative experiments are conducted using several widely known algorithms to evaluate performance. Results demonstrate that the FOPID controller optimised via the proposed MSBWO algorithm significantly outperforms both traditional PID and FOPID controllers tuned by other optimisation strategies, achieving faster convergence, reduced overshoot, and improved stability.

1. Introduction

Recent advancements in computing, electronics, and manufacturing technologies have significantly accelerated research into mobile robotics, enabling their deployment across diverse domains. Mobile robots are increasingly utilised in hazardous environments—such as disaster response, nuclear facilities, and military reconnaissance—where human presence is either risky or infeasible [1]. Additionally, mobile robotic platforms are pivotal in space and underwater exploration, as well as in healthcare, rehabilitation, intelligent transportation, and consumer applications [2].

Among various robotic architectures, two-wheeled self-balancing robots (TWSBRs) have emerged as a distinctive category. Originally conceptualised by Professor Kazuo Yamato at Tokyo Telecom University in the late 1980s, the TWSBR design, illustrated in Figure 1a, offers unique advantages over multi-wheeled robots [3]. Its coaxial wheel structure enables zero-radius turning [4], while its continuous dynamic balancing capability provides robustness against external disturbances [5]. The compact vertical layout of TWSBRs also minimises spatial footprint, making them ideal for constrained indoor environments [6], and enhances human–robot interaction by extending the usable vertical space [7]. Prominent implementations include the Segway [8,9] and uBot platforms [10,11], as shown in Figure 1b and Figure 1c, respectively.

Despite their inherently nonlinear dynamics, two-wheeled self-balancing robots (TWSBRs) are frequently controlled using linearised models, typically justified by small-angle approximations. In this context, Proportional–Integral–Derivative (PID) controllers have remained popular due to their structural simplicity and feasibility for real-time implementation [12]. Numerous studies have demonstrated the effectiveness of PID-controlled TWSBR prototypes [13,14], including Arduino-based implementations [15,16], as well as more advanced designs incorporating laser range sensors [17] and IoT connectivity [18].

Nevertheless, the fractional-order PID (FOPID) controller, derived from fractional calculus, offers greater tuning flexibility and dynamic adaptability through the additional parameters $\lambda$ and $\mu$, extending beyond the conventional PID gains. Comparative studies have consistently demonstrated that FOPID controllers outperform their integer-order counterparts in TWSBR applications, particularly when optimised via heuristic algorithms. For example, Singh and Padhy [19] proposed a ${\mathrm{PI}}^{\lambda }{\mathrm{D}}^{\mu }$ controller optimised with a hybrid PSO–NM strategy, which achieved superior convergence and control accuracy in higher-order processes. Similarly, Zhang et al. [20] integrated fuzzy logic with fractional-order PID control for two-wheeled self-balancing robots on inclined surfaces, demonstrating enhanced robustness and adaptability. These studies underscore the effectiveness of optimisation-based fractional-order control, yet their scope is restricted by reliance on single-strategy search or case-specific implementations. To address these limitations, this work develops a Multi-Strategy Improved Beluga Whale Optimisation (MSBWO) framework that combines chaotic initialisation, elite pool selection, Lévy flight, and golden sine search, thereby enabling more effective FOPID tuning for TWSBRs subject to complex nonlinear dynamics.

The tuning of such controllers is, however, critically dependent on the underlying optimisation strategy [21]. Traditional optimisation methods include gradient descent [22], genetic algorithms [23], particle swarm optimisation (PSO) [24], and differential evolution [25]. More recently, nature-inspired metaheuristics have demonstrated strong performance, such as Dung Beetle Optimisation (DBO) [26], Whale Optimisation Algorithm (WOA) [27], Beluga Whale Optimisation (BWO) [28], and Grey Wolf Optimisation (GWO) [29].

Within the field of nonlinear TWSBR control, FOPID controllers optimised by intelligent algorithms, particularly PSO and its variants, have exhibited enhanced stability, reduced overshoot, and improved robustness against disturbances [30,31,32,33]. Indeed, the adoption of heuristic and hybrid optimisation algorithms for FOPID parameter tuning has become a research focus, given the complexity of optimising five interdependent control parameters. For example, PSO has been successfully employed for trajectory tracking of wheeled mobile robots, yielding more accurate tracking than conventional controllers [34]. Likewise, modified PSO variants have reduced tracking errors in autonomous mobile robots compared with integer-order PID controllers [35]. Beyond PSO, Genetic Algorithm (GA)-tuned FOPID controllers have demonstrated robustness to dynamic uncertainties, while fuzzy inference system (FIS)-based tuning has achieved lower integral-time-absolute-error values [36]. More recently, hybrid schemes, such as the Hybrid Whale–Grey Wolf Optimizer (HWGO), have outperformed single-strategy algorithms by achieving faster convergence and reduced overshoot [37].

Importantly, the effectiveness of FOPID controllers is not limited to simulation. Real-world implementations underscore their practical feasibility. For instance, a fuzzy fractional-order PID (FFOPID) controller was applied to a TWSBR operating on inclined surfaces, demonstrating superior disturbance rejection compared with PID, fuzzy-PID, and standard FOPID controllers. Similarly, cascade control structures combining backstepping and FOPID controllers have been validated on differential wheeled mobile robots, showing notable improvements in trajectory tracking under nonlinear dynamics and actuator saturation [38]. In addition, an Arduino-based implementation of a FOPID controller on the AlphaBot2-Ar mobile robot has confirmed its robustness and effectiveness in real hardware experiments, thereby bridging the gap between theory and practice [39]. These findings collectively confirm the suitability of FOPID-based approaches for both simulation environments and hardware platforms.

With respect to the Beluga Whale Optimizer (BWO), its applications in robotic control remain comparatively limited when set against mainstream optimisers such as PSO and GWO. Nonetheless, BWO’s exploration mechanism and adaptability make it a promising candidate, particularly when hybridised or enhanced with chaotic maps [40]. Building on this foundation, the proposed Multi-Strategy Beluga Whale Optimisation (MSBWO) integrates chaotic mapping and adaptive control factors to alleviate premature convergence and to balance exploration and exploitation. This is especially pertinent for TWSBRs, which are inherently nonlinear, underactuated, and highly sensitive to parameter variations [41,42]. The improvements in MSBWO directly address these challenges by mitigating control chattering, enhancing disturbance rejection, and ensuring smoother stabilisation—issues that conventional optimisers frequently struggle to resolve.

The main contributions of this study are summarised as follows:

1.

A Multi-Strategy Improved Beluga Whale Optimisation (MSBWO) algorithm is proposed, integrating chaotic mapping, elite selection, and hybrid search strategies to enhance both exploration and exploitation capabilities.

2.

A dynamic model of the TWSBR is formulated based on physical parameters, and both FOPID and integer-order PID controllers are designed accordingly.

3.

The MSBWO algorithm and several benchmark optimisers are applied to tune controller parameters. The performance of the optimised controllers is then compared using simulation results under identical operating conditions.

The rest of this paper is organised as follows: Section 2 details the BWO and the proposed MSBWO algorithm. Section 3 introduces the PID and FOPID controllers. Section 4 derives the dynamic model of the TWSBR. Section 5 presents comparative optimisation and control performance analyses. Section 6 concludes the paper.

2. Optimisation Algorithm

The Beluga Whale Optimization (BWO) algorithm, first introduced in 2022, is a nature-inspired metaheuristic technique derived from the social and behavioural characteristics of beluga whales. These marine mammals typically form pods consisting of 2 to 25 individuals, with an average group size of approximately 10. Similar to other metaheuristic algorithms, BWO consists of two main phases: exploration and exploitation. Notably, it also integrates a distinctive diversification mechanism inspired by the “whale fall” phenomenon observed in deep-sea ecosystems. As illustrated in Figure 2, the BWO algorithm models its search process based on three key behavioural patterns of beluga whales.

2.1. Algorithm Overview

2.1.1. Initialisation

In the exploration phase, BWO enhances global search capability by randomising beluga whale movements across the design space. In contrast, the exploitation phase focuses on local refinement. Each beluga whale represents a candidate solution, and its position is continuously updated to navigate the search landscape.

The population of beluga whales is expressed as a matrix:

$$X=\left[\begin{array}{cccc}{x}_{1,1}& x_{1,2}& \dots & x_{1,d}\\ x_{2,1}& x_{2,2}& \dots & x_{2,d}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n,1}& x_{n,2}& \dots & x_{n,d}\end{array}\right]$$

(1)

Here, n denotes the population size and d represents the dimension of the design variables. The fitness values corresponding to each whale are calculated as:

$$F_X=\left[\begin{array}{c}f(x_{1,1},\dots ,x_{1,d})\\ f(x_{2,1},\dots ,x_{2,d})\\ ⋮\\ f(x_{n,1},\dots ,x_{n,d})\end{array}\right]$$

(2)

The switching between exploration and exploitation is governed by the balance factor $B_f$, defined as:

$$B_f=B_0\left(1-{\displaystyle \frac{t}{2T}}\right)$$

(3)

where t is the current iteration, T is the maximum number of iterations, and $B_0\in (0,1)$ is a randomly generated value at each iteration. When $B_f>0.5$, the algorithm is in exploration mode; otherwise, it performs exploitation.

2.1.2. Exploration Phase

This phase mimics the synchronised swimming behaviour of belugas. The updated position of the $i\mathrm{th}$ whale in dimension j is defined as:

$$X_{i,j}^{t+1}=\left\{\begin{array}{cc}{X}_{i,p_j}^t+\left(X_{r,p_1}^t-X_{i,p_j}^t\right)(1+r_1)sin\left(2\pi r_2\right),\hfill & \mathrm{if}j\mathrm{is}\mathrm{even}\hfill \\ X_{i,p_j}^t+\left(X_{r,p_1}^t-X_{i,p_j}^t\right)(1+r_1)cos\left(2\pi r_2\right),\hfill & \mathrm{if}j\mathrm{is}\mathrm{odd}\hfill \end{array}\right.$$

(4)

Here, $X_{i,p_j}^t$ and $X_{r,p_1}^t$ denote the positions of the current and randomly selected whales, while $r_1$ and $r_2$ are random numbers in $(0,1)$ to enhance diversity.

2.1.3. Exploitation (Development) Phase

The development phase emulates belugas’ cooperative hunting. A Lévy flight-based strategy is introduced to strengthen convergence:

$$X_i^{t+1}=r_3{X}_{\mathrm{best}}^t-r_4{X}_i^t+C_1·L_F·(X_r^t-X_i^t)$$

(5)

where $X_{\mathrm{best}}^t$ is the global best position, and $r_3,r_4\in (0,1)$. The Lévy flight factor $L_F$ is computed as:

$$L_F=0.05\times {\displaystyle \frac{u·\sigma }{{\left|v\right|}^{1/\beta }}}$$

(6)

$$\sigma ={\left({\displaystyle \frac{\Gamma (1+\beta )·sin(\pi \beta /2)}{\Gamma ((1+\beta )/2)·\beta ·2^{(\beta -1)/2}}}\right)}^{1/\beta }$$

(7)

with u and v drawn from normal distributions and $\beta =1.5$.

2.1.4. Whale Fall Phase

To model the natural whale fall event, a stochastic mechanism is incorporated. When triggered, it slightly modifies whale positions:

$$X_i^{t+1}=r_5{X}_i^t-r_6{X}_r^t+r_7{X}_{\mathrm{step}}$$

(8)

The step vector $X_{\mathrm{step}}$ is defined as:

$$X_{\mathrm{step}}=(ub-lb)·exp\left(-C_2·{\displaystyle \frac{t}{T}}\right)$$

(9)

Here, $ub$ and $lb$ are the upper and lower bounds of the search space, and $C_2=2W_f·n$, with $W_f$ representing the whale fall probability:

$$W_f=0.1-0.05·{\displaystyle \frac{t}{T}}$$

(10)

This probability linearly decreases over iterations, encouraging early diversification and late convergence.

2.2. Multi-Strategy Improved Beluga Whale Optimization (MSBWO)

2.2.1. Enhanced Population Initialisation

The performance of population-based metaheuristic algorithms heavily depends on the quality and diversity of the initial population. In standard BWO, purely random initialisation may lead to uneven population distribution, limiting global exploration capability. To overcome this, chaotic mapping is integrated due to its inherent randomness and ergodicity [43].

Among several chaotic maps (e.g., Logistic, Tent, Circle), the Circle map is selected owing to its broader phase space coverage. To further enhance uniformity and improve convergence, an improved version of the Circle map is adopted, modifying its amplitude and frequency parameters [44]. In particular, the introduction of the Improved Circle chaotic map enhances the exploration capability of the proposed MSBWO algorithm. By generating a more uniformly distributed and ergodic initial population, it effectively mitigates premature convergence in the high-dimensional and strongly coupled FOPID parameter space, which is critical for stabilising the multi-variable TWSBR dynamics. Moreover, this mechanism improves the balance between global search and local exploitation, thereby enabling the controller to achieve faster convergence while maintaining robustness against parameter uncertainties and external disturbances.

The standard Circle chaotic map is defined as:

$$x_{n+1}=mod\left(x_n+0.2-{\displaystyle \frac{0.5}{3\pi }}sin\left(2\pi x_n\right),1\right)$$

(11)

The improved Circle chaotic map becomes:

$$x_{n+1}=mod\left(3.85x_n+0.4-{\displaystyle \frac{0.7}{3.85\pi }}sin\left(3.85\pi x_n\right),1\right)$$

(12)

Figure 3 illustrates the distributions generated by random initialisation, standard Circle mapping, and the improved Circle mapping. It is evident that the improved Circle map provides a more uniform distribution, which significantly enhances population diversity and facilitates broader coverage of the search space.

2.2.2. Elite Pool Strategy

In metaheuristic algorithms such as Gray Wolf Optimization (GWO), relying exclusively on the best-performing individual to guide the search process may lead to premature convergence. To overcome this limitation, GWO incorporates information from multiple elite agents to enhance exploration. Drawing inspiration from this mechanism, the proposed Multi-Strategy Beluga Whale Optimization (MSBWO) algorithm adopts an elite pool strategy, which utilises the top three candidate solutions along with their weighted average to guide the position update process [45]. Figure 4 illustrates the influence of the elite pool during the global search phase. As shown in the figure, the integration of multiple elite solutions enables a more balanced and diversified search trajectory, helping the algorithm to avoid stagnation in local optima and enhancing its global optimisation capability.The Elite pool strategy further strengthens the exploitation phase by preserving a subset of the best-performing solutions across generations. This mechanism prevents entrapment in local minima caused by the nonlinear couplings between tilt angle and position states in the TWSBR model. By reintroducing elite individuals into the evolutionary process, the algorithm maintains solution diversity and guides the search trajectory towards more promising regions of the parameter space. Consequently, the optimisation process achieves higher stability and accuracy, ensuring that the resulting FOPID controller exhibits reliable performance under strongly nonlinear and underactuated dynamics.

The elite pool vector $e^T$ is constructed as:

$$\mathrm{Elite}{e}^T=\left[X_{\mathrm{best}1}^T,X_{\mathrm{best}2}^T,X_{\mathrm{best}3}^T,X_{\mathrm{mean}}^T\right]$$

(13)

where the weighted average elite position $X_{\mathrm{mean}}^T$ is computed as:

$$X_{\mathrm{mean}}^T=\sum _{i=1}^3{\theta }_i{X}_i^T$$

(14)

The weights ${\theta }_i$ are determined based on the fitness of each elite solution:

$$w_i={\displaystyle \frac{3f_{\mathrm{best}3}-f_i}{3f_{\mathrm{best}3}-f_{\mathrm{best}1}}},{\theta }_i={\displaystyle \frac{w_i}{{\sum }_j{w}_j}}$$

(15)

where, $f_i$ is the fitness value of the ith elite individual. This approach integrates fitness-based weighting, ensuring that more promising solutions have greater influence on the search direction. As a result, the elite pool strategy not only enhances convergence speed but also improves the algorithm’s capability to escape local optima.

2.2.3. Development Stage: Integration of Adaptive Lévy Flight and Spiral Search

In the original Beluga Whale Optimization (BWO) algorithm, the development phase employs a fixed-step Lévy flight mechanism to balance exploration and exploitation. However, using a constant step size parameter, denoted as $\alpha$, may not be suitable for all iterations. Specifically, a larger $\alpha$ tends to enhance the algorithm’s global search capability but often results in reduced solution accuracy. Conversely, a smaller $\alpha$ can improve local exploitation and precision, yet may significantly slow down the convergence speed.

To illustrate this trade-off, Figure 5 shows the variation of Lévy flight step sizes and their influence on the step length distribution. The figure highlights how different values of $\alpha$ affect the spread and concentration of the search steps, thereby impacting the overall search dynamics of the algorithm. The Adaptive Lévy flight and spiral search mechanism is incorporated to dynamically balance exploration and exploitation throughout the optimisation process. By adaptively adjusting the step size and search pattern, it allows the algorithm to escape from local optima while intensifying the search around promising regions. This dual capability accelerates the transient response of the optimised controller and enhances its robustness to external disturbances and modelling uncertainties inherent in TWSBR systems. As a result, the proposed FOPID controller achieves faster convergence without sacrificing stability, even under rapidly varying or highly nonlinear operating conditions.

The Lévy flight step is modelled as:

$$\begin{array}{cc}\hfill & L^{\prime }evy=0.01\times {\displaystyle \frac{u\times \sigma }{{\left|y\right|}^{1/\beta }}}\hfill \\ \hfill & \sigma ={\left({\displaystyle \frac{\Gamma (1+\beta )sin(\pi \beta /2)}{\Gamma ((1+\beta )/2)\beta 2^{(\beta -1)/2}}}\right)}^{1/\beta }\hfill \end{array}$$

(16)

where u and y are normally distributed variables, $\beta \in (1,2)$ is the stability parameter of the Lévy distribution, and $\sigma$ is the scale parameter computed via Gamma functions.

To address dynamic exploration requirements, this paper introduces an adaptive Lévy step strategy. Early iterations adopt larger step sizes to explore globally, while smaller steps are used in later iterations for fine local tuning.

Moreover, the original BWO development phase may overlook intermediate search zones. To improve local exploitation, a spiral search mechanism, inspired by the Whale Optimization Algorithm (WOA), is integrated. This spiral model promotes directed motion between current and elite individuals based on relative distance and angular position.

The enhanced position update equation is:

$$X_i^{T+1}=r_3·{\mathrm{Elite}}^T-r_4·X_i^T+C_1·L_F·(X_r^T-X_i^T)+|{\mathrm{Elite}}^T-X_i^T|·cos\left(2\pi l\right)·e^{bl}$$

(17)

where $X_i^{T+1}$ is the updated position of the i-th agent, $X_r^T$ is a randomly chosen individual, $l\in (0,1)$ is a spiral control variable, and b controls the spiral tightness. The coefficient $C_1=2r_4(1-T/T_{max})$ and the adaptive Lévy term $L_F$ are defined as:

$$L_F=0.05\left(1-{\displaystyle \frac{T}{T_{max}}}\right)e^{-T/T_{max}}·{\displaystyle \frac{uv}{{\left|v\right|}^{1/\beta }}}$$

(18)

2.2.4. Golden Sine Strategy

The Golden Sine Algorithm (Golden-SA) [46], proposed by Tanyildizi et al., integrates the periodic behaviour of sine functions with the geometric characteristics of the golden ratio to enhance global search performance. By incorporating both nonlinear oscillatory dynamics and an optimal proportion-based search mechanism, Golden-SA enables efficient exploration of the solution space while maintaining convergence stability.

Figure 6 illustrates the mechanism by which the Golden Sine strategy is applied in the elite-based update process. The combination of sine function modulation and golden section positioning guides the search agents toward promising regions, enhancing both exploration and convergence accuracy. The Golden Sine strategy is introduced to strengthen the global search ability of the optimisation process. By exploiting the periodic and nonlinear properties of the sine function combined with the golden ratio principle, this strategy promotes a more diverse exploration of the search space and reduces the likelihood of premature convergence. Such an enhancement is particularly beneficial for handling the non-affine and underactuated nature of TWSBR dynamics, where the control design requires overcoming strong nonlinearities and limited actuation. Consequently, the integration of the Golden Sine strategy enables the proposed FOPID controller to identify more globally optimal solutions, ensuring improved stability and adaptability under complex operating scenarios.

To further enhance MSBWO’s global exploration and convergence, this strategy is incorporated into the population update process. The update rule is formulated as:

$$X_i^{T+1}=X_i^{T+1}·|sin{R}_1|+r_{1}sin\left(2\pi r_2\right)·|x_1·{\mathrm{Elite}}^T-x_2·X_i^{T+1}|$$

(19)

where $r_1,r_2\in (0,1)$ and $R_1\in [0,2\pi ]$ are random variables. The coefficients $x_1$ and $x_2$ are determined using golden ratio interpolation:

$$\begin{array}{c}{x}_1=\alpha (1-\tau )+\beta \tau ,x_2=\alpha \tau +\beta (1-\tau ),\\ \tau ={\displaystyle \frac{\sqrt{5}-1}{2}}\end{array}$$

(20)

where, $\alpha$ and $\beta$ are interval bounds for position updates. The golden ratio $\tau$ ensures balanced exploitation and exploration.

The detailed procedures of the proposed Multi-Strategy Beluga Whale Optimization (MSBWO) algorithm are outlined in Algorithm 1. The algorithm incorporates several enhanced strategies, including adaptive Lévy flight, spiral search dynamics, elite pool guidance, and the Golden Sine mechanism, in order to maintain a balanced exploration–exploitation trade-off and improve convergence performance.

In conclusion, the proposed MSBWO algorithm integrates multiple complementary mechanisms—namely, adaptive Lévy flight, spiral search, elite pool guidance, and the Golden Sine strategy—to significantly improve the balance between global exploration and local exploitation. These enhancements are specifically designed to overcome the limitations of the original BWO and to enhance convergence robustness in solving complex optimisation problems.

Figure 7 presents the overall flowchart of the MSBWO algorithm, where the proposed improvements are highlighted in red for clarity.

Algorithm 1 The pseudo code of the proposed MSBWO algorithm

Require:  Algorithmic parameters (population size, maximum iterations) Ensure:  Best solution $P^{*}$ 1:  Calculate the improved circular chaos map using Equation (12); 2:  Initialise population A, B, C, and evaluate fitness values to obtain the best solution $P^{*}$; 3:  while $T\le T_{\max }$  do 4:       Compute whale fall probability $W_f$ via Equation (10), balance factor $B_f$ via Equation (3), and update elite pool using Equation (13); 5:       for each beluga whale $X_i$ do 6:            if $B_f\left(i\right)>0.5$ then 7:                // Exploration phase 8:                Randomly generate $p_j$, where $j=1,2,\dots ,d$; 9:                Select a random beluga whale $X_r$; 10:              Update position of $X_i$ using Equation (12); 11:          else 12:               // Exploitation phase 13:               Update jump strength $C_1$ and compute adaptive Lévy flight; 14:               Update position of $X_i$ using Equation (17); 15:          end if 16:          Apply boundary checking and evaluate fitness; 17:      end for 18:      for each beluga whale $X_i$ do 19:           if $B_f\left(i\right)\le C_f$ then 20:               // Whale fall phase 21:               Update step factor $C_2$ and compute step size $X_{\mathrm{step}}$; 22:               Update position using Equation (17), then check boundaries and compute fitness; 23:           end if 24:      end for 25:      for each beluga whale $X_i$ do 26:           // Golden Sine strategy 27:           Update position using Equation (19), then check boundaries and compute fitness; 28:      end for 29:      Identify current best solution $P^{*}$; 30:      Increment iteration: $T\leftarrow T+1$; 31:  end while  32:  return Best solution $P^{*}$

3. PID and FOPID Control Design

The Fractional-Order Proportional-Integral-Derivative (FOPID) controller, denoted as ${\mathrm{PI}}^{\lambda }{\mathrm{D}}^{\mu }$, generalises the classical PID controller by extending the integral and derivative terms to arbitrary positive real orders. Its transfer function in the Laplace domain is given by:

$$C_{\mathrm{FOPID}}\left(s\right)={\displaystyle \frac{U\left(s\right)}{E\left(s\right)}}=K_p+{\displaystyle \frac{K_i}{s^{\lambda }}}+K_d{s}^{\mu },(\lambda ,\mu >0)$$

(21)

Here, $K_p$, $K_i$, and $K_d$ are the proportional, integral, and derivative gains, respectively, while $\lambda$ and $\mu$ represent the fractional orders of integration and differentiation. When both $\lambda =1$ and $\mu =1$, the controller reduces to the classical integer-order PID form:

$$C_{\mathrm{PID}}\left(s\right)={\displaystyle \frac{U\left(s\right)}{E\left(s\right)}}=K_p+{\displaystyle \frac{K_i}{s}}+K_{d}s$$

(22)

In this formulation, $U\left(s\right)$ and $E\left(s\right)$ denote the output and input signals in the Laplace domain, respectively.

3.1. Fractional Calculus Foundations

Fractional calculus is a branch of mathematical analysis that generalises traditional calculus by allowing differentiation and integration to non-integer (real or complex) orders. This extension offers improved modelling fidelity for dynamic systems exhibiting memory and hereditary properties.

The general operator for fractional calculus is defined as:

$$t_0{D}_t^k=\left\{\begin{array}{cc}{\displaystyle \frac{d^k}{d{t}^k}},\hfill & k>0\hfill \\ 1,\hfill & k=0\hfill \\ {\int }_{t_0}^t{\left(dt\right)}^{-k},\hfill & k<0\hfill \end{array}\right.$$

(23)

Several formal definitions of fractional derivatives exist, among which the Riemann-Liouville (RL), Caputo (C), and Grünwald–Letnikov (GL) formulations are most prevalent.

The Riemann–Liouville fractional derivative of order k, where $n-1<k<n$, is given by:

$${}_{t_0}{}^{\mathrm{RL}}D_t^{k}f\left(t\right)={\displaystyle \frac{1}{\Gamma (n-k)}}{\displaystyle \frac{d^n}{d{t}^n}}{\int }_{t_0}^t{\displaystyle \frac{f\left(\tau \right)}{{(t-\tau )}^{k-n+1}}}d\tau$$

(24)

The Euler Gamma function used above is defined as:

$$\Gamma \left(k\right)={\int }_0^{\infty }{e}^{-u}{u}^{k-1}du,k>0$$

(25)

The Caputo definition, often preferred in control applications due to its compatibility with physically meaningful initial conditions, is:

$${}_{t_0}{}^{\mathrm{C}}D_t^{k}f\left(t\right)={\displaystyle \frac{1}{\Gamma (n-k)}}{\int }_{t_0}^t{\displaystyle \frac{f^{\left(n\right)}\left(\tau \right)}{{(t-\tau )}^{k-n+1}}}d\tau$$

(26)

The Grünwald–Letnikov (GL) derivative is expressed as a limit:

$${}_{t_0}{}^{\mathrm{GL}}D_t^{k}f\left(t\right)=\underset{h\to 0}{lim}{\displaystyle \frac{1}{h^k}}\sum _{i=0}^{[(t-t_0)/h]}{(-1)}^i\left({\displaystyle \genfrac{}{}{0pt}{}{k}{i}}\right)f(t-ih)$$

(27)

The binomial coefficient for real k is defined using the Gamma function:

$$\left({\displaystyle \genfrac{}{}{0pt}{}{k}{i}}\right)={\displaystyle \frac{\Gamma (k+1)}{\Gamma (i+1)\Gamma (k-i+1)}}$$

(28)

3.2. Approximation of Fractional Operators

Fractional-order operators are inherently infinite-dimensional, posing challenges for real-time implementation. To address this, rational approximations such as Oustaloup’s Recursive Approximation (ORA) are widely adopted. It approximates the operator $s^{\alpha }$ over a finite frequency band:

$$s^{\alpha }\approx K\prod _{k=-N}^N{\displaystyle \frac{s+{\omega }_k^{\prime }}{s+{\omega }_k}}$$

(29)

The poles ${\omega }_k$, zeros ${\omega }_k^{\prime }$, and gain K are calculated as:

$${\omega }_k={\omega }_l{\left({\displaystyle \frac{{\omega }_h}{{\omega }_l}}\right)}^{\frac{k+N+0.5(1+\alpha )}{2N+1}}$$

(30)

$${\omega }_k^{\prime }={\omega }_l{\left({\displaystyle \frac{{\omega }_h}{{\omega }_l}}\right)}^{\frac{k+N+0.5(1-\alpha )}{2N+1}}$$

(31)

$$K={\omega }_h^{\alpha }$$

(32)

Here, $\alpha$ is the fractional order to approximate, N is the approximation order, and $({\omega }_l,{\omega }_h)$ is the target frequency range. In this study, a 4th-order Oustaloup filter is utilised over the frequency band $[{10}^{-2},{10}^2]\mathrm{rad}/\mathrm{s}$.

4. Dynamic Modelling of the TWSBR

The structural configuration of the two-wheeled self-balancing robot (TWSBR) is depicted in Figure 8a. The system consists of a central body mounted on two independently actuated wheels. As an underactuated mechanical system, the TWSBR possesses two control inputs and three degrees of freedom, allowing it to be decomposed into two decoupled subsystems for analysis and control design.

The first subsystem, referred to as the $\varphi$-subsystem, governs the yaw dynamics and is controlled by the input $u_2=v_l-v_r$, which corresponds to the differential velocities of the left and right wheels. The second subsystem, defined over the state pair $\{\theta ,\psi \}$, manages translational and pitch motions and is driven by the input $u_1=v_l+v_r$, which is primarily responsible for maintaining balance.

The reference trajectories ${\theta }_d\left(t\right)$, ${\psi }_d\left(t\right)$, and ${\varphi }_d\left(t\right)$ are assumed to be bounded and twice continuously differentiable. Higher-order dynamics are neglected in the modelling process, and appropriate smoothness conditions are imposed on ${\psi }_d\left(t\right)$ to facilitate controller design and ensure theoretical guarantees.

Figure 8b,c present the side and top views of the TWSBR, respectively, including its coordinate configuration. The physical parameters used for dynamic modelling are listed in

Table 1. Physical parameters of the two-wheeled self-balancing robot (TWSBR).

Parameter	Description
$g=9.81\mathrm{m}/{\mathrm{s}}^2$	Gravitational acceleration
$m=0.051\mathrm{kg}$	Mass of each wheel
$R=0.0325\mathrm{m}$	Radius of each wheel
$J_W={\displaystyle \frac{1}{2}}m{R}^2\mathrm{kg}·{\mathrm{m}}^2$	Moment of inertia of each wheel
$M=0.703\mathrm{kg}$	Mass of the robot body
$W=0.192\mathrm{m}$	Width of the robot body
$D=0.082\mathrm{m}$	Depth of the robot body
$H=0.112\mathrm{m}$	Height of the robot body
$L={\displaystyle \frac{H}{2}}\mathrm{m}$	Distance from wheel axle to the centre of mass
$J_{\psi }={\displaystyle \frac{1}{3}}M{L}^2\mathrm{kg}·{\mathrm{m}}^2$	Pitch moment of inertia of the body
$J_{\varphi }={\displaystyle \frac{1}{12}}M(W^2+D^2)\mathrm{kg}·{\mathrm{m}}^2$	Yaw moment of inertia of the body
$J_m=1\times {10}^{-5}\mathrm{kg}·{\mathrm{m}}^2$	Moment of inertia of the DC motor
$R_m=2.9\Omega$	Armature resistance of the DC motor
$K_b=0.024\mathrm{V}·\mathrm{s}/\mathrm{rad}$	Back electromotive force (EMF) constant
$K_t=0.025\mathrm{Nm}/\mathrm{A}$	Torque constant of the motor
$n=30$	Gear ratio
$f_m=0.0022$	Friction coefficient between motor and body
$f_W=0$	Friction coefficient between wheel and ground

. Parameters such as the motor radius $R_M$, back EMF constant $K_b$, and torque constant $K_t$ are adopted from the LEGO NXT specifications [47]. Other parameters—such as the motor inertia $J_m$, gear ratio n, and friction coefficients $f_m$ and $f_W$—are identified through experimental estimation, owing to practical measurement constraints.

4.1. Motion Equations of TWSBR

Based on the coordinate systems shown in Figure 8b,c, the motion equations of the TWSBR are derived using the Lagrangian method. Assuming that the motion direction at time $t=0$ is aligned with the positive x-axis, the following coordinate definitions are established:

$$\begin{array}{cc}\hfill & (\theta ,\varphi )=\left({\displaystyle \frac{1}{2}}({\theta }_l+{\theta }_r),{\displaystyle \frac{R}{W}}({\theta }_r-{\theta }_l)\right)\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & (x_m,y_m,z_m)=\left(\int {\dot{x}}_{m}dt,\int {\dot{y}}_{m}dt,R\right)\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & ({\dot{x}}_m,{\dot{y}}_m)=(R\dot{\theta }cos\varphi ,R\dot{\theta }sin\varphi )\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & (x_l,y_l,z_l)=(x_m-{\displaystyle \frac{W}{2}}sin\varphi ,y_m+{\displaystyle \frac{W}{2}}cos\varphi ,z_m)\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & (x_r,y_r,z_r)=(x_m+{\displaystyle \frac{W}{2}}sin\varphi ,y_m-{\displaystyle \frac{W}{2}}cos\varphi ,z_m)\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & (x_b,y_b,z_b)=(x_m+Lsin\psi cos\varphi ,y_m+Lsin\psi sin\varphi ,z_m+Lcos\psi )\hfill \end{array}$$

(38)

$\psi$ denotes the body pitch angle, ${\theta }_{l,r}$ are the angular positions of the left and right wheels, and ${\theta }_{m_{l,r}}$ represent the DC motor angles. The coordinates $(x_m,y_m,z_m)$, $(x_l,y_l,z_l)$, $(x_r,y_r,z_r)$, and $(x_b,y_b,z_b)$ correspond to the center of the TWSBR, the left wheel, the right wheel, and the center of gravity, respectively.

The translational kinetic energy $T_1$, rotational kinetic energy $T_2$, and potential energy U are given as:

$$\begin{array}{cc}\hfill T_1& ={\displaystyle \frac{1}{2}}m({\dot{x}}_l^2+{\dot{y}}_l^2+{\dot{z}}_l^2)+{\displaystyle \frac{1}{2}}m({\dot{x}}_r^2+{\dot{y}}_r^2+{\dot{z}}_r^2)+{\displaystyle \frac{1}{2}}M({\dot{x}}_b^2+{\dot{y}}_b^2+{\dot{z}}_b^2)\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill T_2& ={\displaystyle \frac{1}{2}}{J}_w{\dot{\theta }}_l^2+{\displaystyle \frac{1}{2}}{J}_w{\dot{\theta }}_r^2+{\displaystyle \frac{1}{2}}{J}_{\psi }{\dot{\psi }}^2+{\displaystyle \frac{1}{2}}{J}_{\varphi }{\dot{\varphi }}^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{n}^2{J}_m{({\dot{\theta }}_l-\dot{\psi })}^2+{\displaystyle \frac{1}{2}}{n}^2{J}_m{({\dot{\theta }}_r-\dot{\psi })}^2\hfill \end{array}$$

(40)

$$\begin{array}{c}\hfill U=mg{z}_l+mg{z}_r+Mg{z}_b\end{array}$$

(41)

The fifth and sixth terms in $T_2$ correspond to the rotational kinetic energy of the armature in the left and right DC motors. The Lagrangian L is then defined as:

$$\begin{array}{c}\hfill L=T_1+T_2+U\end{array}$$

(42)

The generalised coordinates used are $\theta$ (average wheel angle), $\psi$ (body pitch angle), and $\varphi$ (yaw angle). The corresponding Lagrange equations are:

$${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial \dot{\theta }}}\right)-{\displaystyle \frac{\partial L}{\partial \theta }}=F_{\theta }$$

(43)

$${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial \dot{\psi }}}\right)-{\displaystyle \frac{\partial L}{\partial \psi }}=F_{\psi }$$

(44)

$${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial L}{\partial \dot{\varphi }}}\right)-{\displaystyle \frac{\partial L}{\partial \varphi }}=F_{\varphi }$$

(45)

The following dynamic equations are derived by applying the Euler–Lagrange method to Equations (43)–(45):

$$\begin{array}{cc}\hfill & \left[(2m+M)R^2+2J_w+2n^2{J}_m\right]\ddot{\theta }+(MLRcos\psi -2n^2{J}_m)\ddot{\psi }\hfill \\ \hfill & -MLR{\dot{\psi }}^{2}sin\psi =F_{\theta }\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill & (MLRcos\psi -2n^2{J}_m)\ddot{\theta }+(M{L}^2+J_{\psi }+2n^2{J}_m)\ddot{\psi }\hfill \\ \hfill & -MgLsin\psi -M{L}^2{\dot{\varphi }}^{2}sin\psi cos\psi =F_{\psi }\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill & \left[\frac{1}{2}m{W}^2+J_{\varphi }+\frac{W^2}{2R^2}(J_w+n^2{J}_m)+M{L}^2{sin}^2\psi \right]\ddot{\varphi }\hfill \\ \hfill & +2M{L}^2\dot{\psi }\dot{\varphi }sin\psi cos\psi =F_{\varphi }\hfill \end{array}$$

(48)

Considering the torques generated by the DC motors and viscous friction, the generalised forces are expressed as:

$$\begin{array}{c}\hfill (F_{\theta },F_{\psi },F_{\varphi })=\left(F_l+F_r,F_{\psi },{\displaystyle \frac{W}{2R}}(F_r-F_l)\right)\end{array}$$

(49)

The torques from the left and right motors are modelled as:

$$\begin{array}{c}\hfill F_l=n{K}_t{i}_l+f_m(\dot{\psi }-{\dot{\theta }}_l)-f_w{\dot{\theta }}_l\end{array}$$

(50)

$$\begin{array}{c}\hfill F_r=n{K}_t{i}_r+f_m(\dot{\psi }-{\dot{\theta }}_r)-f_w{\dot{\theta }}_r\end{array}$$

(51)

$$\begin{array}{c}\hfill F_{\psi }=-n{K}_t(i_l+i_r)-f_m(2\dot{\psi }-{\dot{\theta }}_l-{\dot{\theta }}_r)\end{array}$$

(52)

Here, $i_{l,r}$ represent the currents of the DC motors. Since DC motors are voltage-driven via pulse-width modulation (PWM), current is indirectly controlled through motor voltage. Assuming negligible motor inductance, the motor model becomes:

$$\begin{array}{c}\hfill L_m{\dot{i}}_{l,r}=v_{l,r}+K_b(\dot{\psi }-{\dot{\theta }}_{l,r})-R_m{i}_{l,r}\end{array}$$

(53)

Neglecting the inductance ($L_m\approx 0$), the steady-state current is:

$$\begin{array}{c}\hfill i_{l,r}={\displaystyle \frac{v_{l,r}+K_b(\dot{\psi }-{\dot{\theta }}_{l,r})}{R_m}}\end{array}$$

(54)

Substituting into the generalised force equations yields:

$$\begin{array}{c}\hfill F_{\theta }=\alpha (v_l+v_r)-2(\beta +f_w)\dot{\theta }+2\beta \dot{\psi }\end{array}$$

(55)

$$\begin{array}{c}\hfill F_{\psi }=-\alpha (v_l+v_r)+2\beta \dot{\theta }-2\beta \dot{\psi }\end{array}$$

(56)

$$\begin{array}{c}\hfill F_{\varphi }={\displaystyle \frac{W}{2R}}\alpha (v_r-v_l)-{\displaystyle \frac{W^2}{2R^2}}(\beta +f_w)\dot{\varphi }\end{array}$$

(57)

The parameters $\alpha$ and $\beta$ are defined as:

$$\begin{array}{c}\hfill \alpha ={\displaystyle \frac{n{K}_t}{R_m}},\beta ={\displaystyle \frac{n{K}_t{K}_b}{R_m}}+f_m\end{array}$$

(58)

4.2. State Equations of TWSBR

The state equations of the TWSBR are derived using modern control theory by linearising the nonlinear dynamics around the upright equilibrium point. Specifically, under the assumption that the tilt angle $\psi$ is small (i.e., $\psi \to 0$), we apply the approximations $sin\psi \approx \psi$ and $cos\psi \approx 1$. Neglecting second-order nonlinear terms such as ${\dot{\psi }}^2$, the simplified motion equations from Equations (46)–(48) become:

$$\begin{array}{cc}\hfill & \left(2m+M\right)R^2+2J_w+2n^2{J}_m\ddot{\theta }\hfill \\ \hfill & +\left(MLR-2n^2{J}_m\right)\ddot{\psi }=F_{\theta }\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill & \left(MLR-2n^2{J}_m\right)\ddot{\theta }+\left(M{L}^2+J_{\psi }+2n^2{J}_m\right)\ddot{\psi }\hfill \\ \hfill & -MgL\psi =F_{\psi }\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill & \left[{\displaystyle \frac{1}{2}}m{W}^2+J_{\varphi }+{\displaystyle \frac{W^2}{2R^2}}\left(J_w+n^2{J}_m\right)\right]\ddot{\varphi }=F_{\varphi }\hfill \end{array}$$

(61)

Equations (59) and (60) form a coupled subsystem in terms of $\theta$ and $\psi$, while Equation (61) is decoupled and contains only $\varphi$.

The system can be expressed in a compact matrix form as:

$$E\left[\begin{array}{c}\ddot{\theta }\\ \ddot{\psi }\end{array}\right]+F\left[\begin{array}{c}\dot{\theta }\\ \dot{\psi }\end{array}\right]+G\left[\begin{array}{c}\theta \\ \psi \end{array}\right]=H\left[\begin{array}{c}{v}_l\hfill \\ v_r\hfill \end{array}\right]$$

(62)

where the coefficient matrices are defined as:

$$E=\left[\begin{array}{cc}(2m+M)R^2+2J_w+2n^2{J}_m& MLR-2n^2{J}_m\\ MLR-2n^2{J}_m& M{L}^2+J_{\psi }+2n^2{J}_m\end{array}\right],$$

$$F=2\left[\begin{array}{cc}\beta +f_w& -\beta \\ -\beta & \beta \end{array}\right],G=\left[\begin{array}{cc}0& 0\\ 0& -MgL\end{array}\right],$$

$$H=\left[\begin{array}{cc}\alpha & \alpha \\ -\alpha & -\alpha \end{array}\right]$$

Let the state vector ${\mathbf{x}}_1$ and input vector $\mathbf{u}$ be defined as:

$${\mathbf{x}}_1={\left[\begin{array}{cccc}\theta ,\hfill & \psi ,\hfill & \dot{\theta },\hfill & \dot{\psi }\hfill \end{array}\right]}^T,\mathbf{u}={\left[\begin{array}{cc}{v}_l,\hfill & v_r\hfill \end{array}\right]}^T$$

The state-space representation of the TWSBR becomes:

$$\begin{array}{cc}\hfill & {\dot{\mathbf{x}}}_1=A_1{\mathbf{x}}_1+B_1\mathbf{u}\hfill \end{array}$$

(63)

where

$$\begin{array}{c}\hfill A_1=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& A_1(3,2)& A_1(3,3)& A_1(3,4)\\ 0& A_1(4,2)& A_1(4,3)& A_1(4,4)\end{array}\right]\end{array}$$

(64)

$$\begin{array}{c}\hfill B_1=\left[\begin{array}{cc}0& 0\\ 0& 0\\ B_1\left(3\right)& B_1\left(3\right)\\ B_1\left(4\right)& B_1\left(4\right)\end{array}\right]\end{array}$$

(65)

The symbolic expressions are as follows:

$$\begin{array}{cc}\hfill & A_1(3,2)=-gMLE(1,2)/det\left(E\right),\hfill \\ \hfill & A_1(4,2)=gMLE(1,1)/det\left(E\right),\hfill \\ \hfill & A_1(3,3)=-2[(\beta +f_w)E(2,2)+\beta E(1,2)]/det\left(E\right),\hfill \\ \hfill & A_1(4,3)=2[(\beta +f_w)E(1,2)+\beta E(1,1)]/det\left(E\right),\hfill \\ \hfill & A_1(3,4)=2\beta [E(2,2)+E(1,2)]/det\left(E\right),\hfill \\ \hfill & A_1(4,4)=-2\beta [E(1,1)+E(1,2)]/det\left(E\right),\hfill \\ \hfill & B_1\left(3\right)=\alpha [E(2,2)+E(1,2)]/det\left(E\right),\hfill \\ \hfill & B_1\left(4\right)=-\alpha [E(1,1)+E(1,2)]/det\left(E\right),\hfill \\ \hfill & det\left(E\right)=E(1,1)E(2,2)-E{(1,2)}^2\hfill \end{array}$$

Substituting the system parameters from Table 1, the balanced subsystem is given as:

$$\begin{gathered} \left[\begin{array}{c}\dot{\theta }\\ \dot{\psi }\\ \ddot{\theta }\\ \ddot{\psi }\end{array}\right]=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& 55.540& -0.610& 0.610\\ 0& 62.794& 0.316& -0.316\end{array}\right]\left[\begin{array}{c}\theta \\ \psi \\ \dot{\theta }\\ \dot{\psi }\end{array}\right] \\ +\left[\begin{array}{cc}0& 0\\ 0& 0\\ 9.385& 9.385\\ -4.857& -4.857\end{array}\right]\left[\begin{array}{c}{v}_l\\ v_r\end{array}\right] \end{gathered}$$

(66)

From the derived state-space form, it can be verified that the system is both fully controllable and observable.

5. Simulations

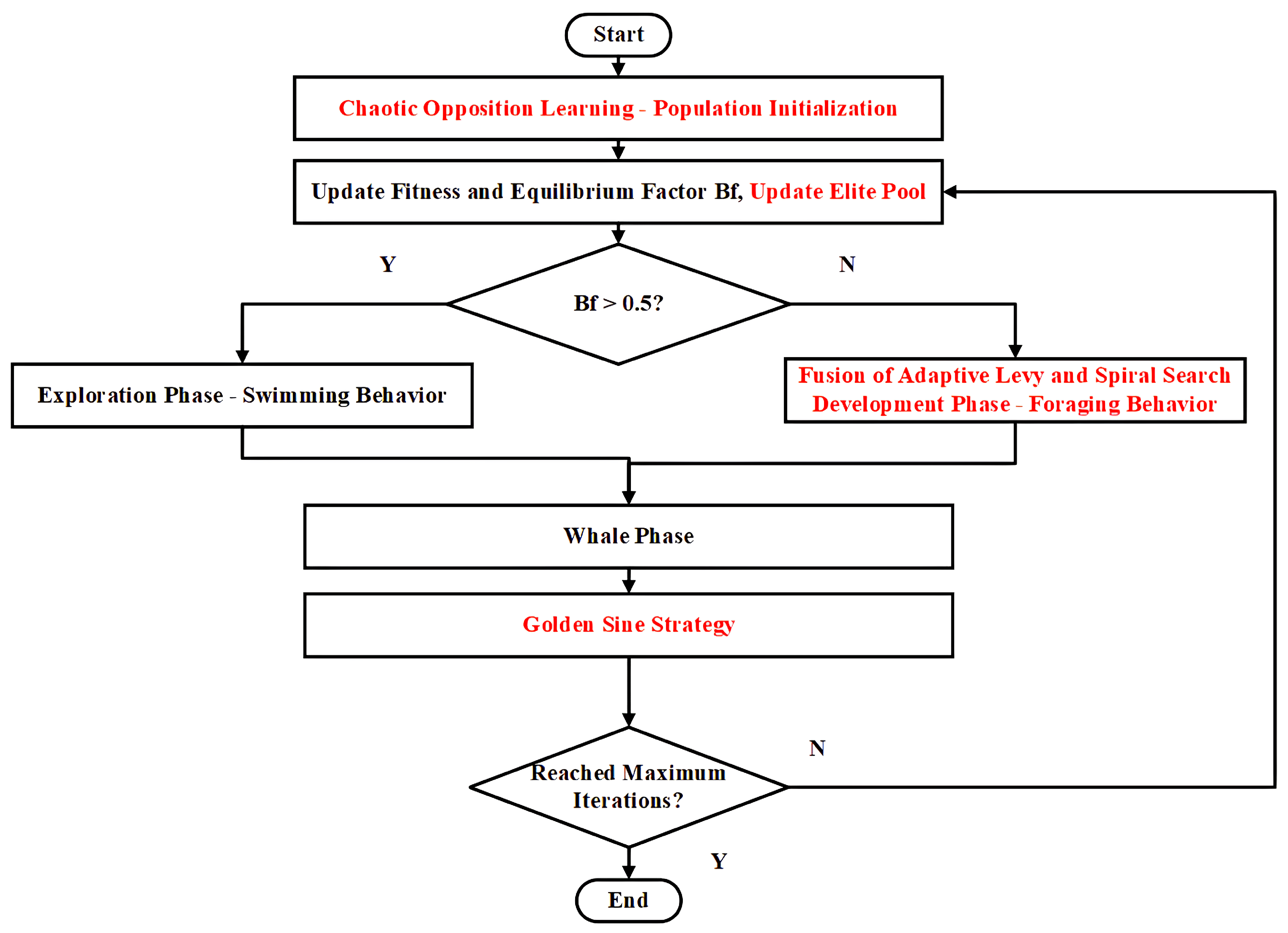
5.1. Performance of the MSBWO Algorithm

In this study, several well-established swarm intelligence algorithms were selected for performance comparison with the proposed Multi-Strategy Improved Beluga Whale Optimization (MSBWO) algorithm. The benchmark algorithms include Particle Swarm Optimization (PSO), Whale Optimization Algorithm (WOA), Dung Beetle Optimization (DBO), Gray Wolf Optimization (GWO), and the original Beluga Whale Optimization (BWO). All of these approaches are nature-inspired metaheuristic algorithms derived from the collective behaviours of animals. These algorithms were chosen due to their popularity, demonstrated effectiveness, and relevance in solving complex optimisation problems.

Table 2. Key hyperparameters of the proposed MSBWO algorithm.

Parameter	Value
Population size	30
Max iterations (PID)	200
Max iterations (FOPID)	400
Lévy flight index $\beta$	1.5
Whale fall probability $W_f$	0.1
Spiral control factor b	1
Elite pool size	Top 3 candidates + weighted average
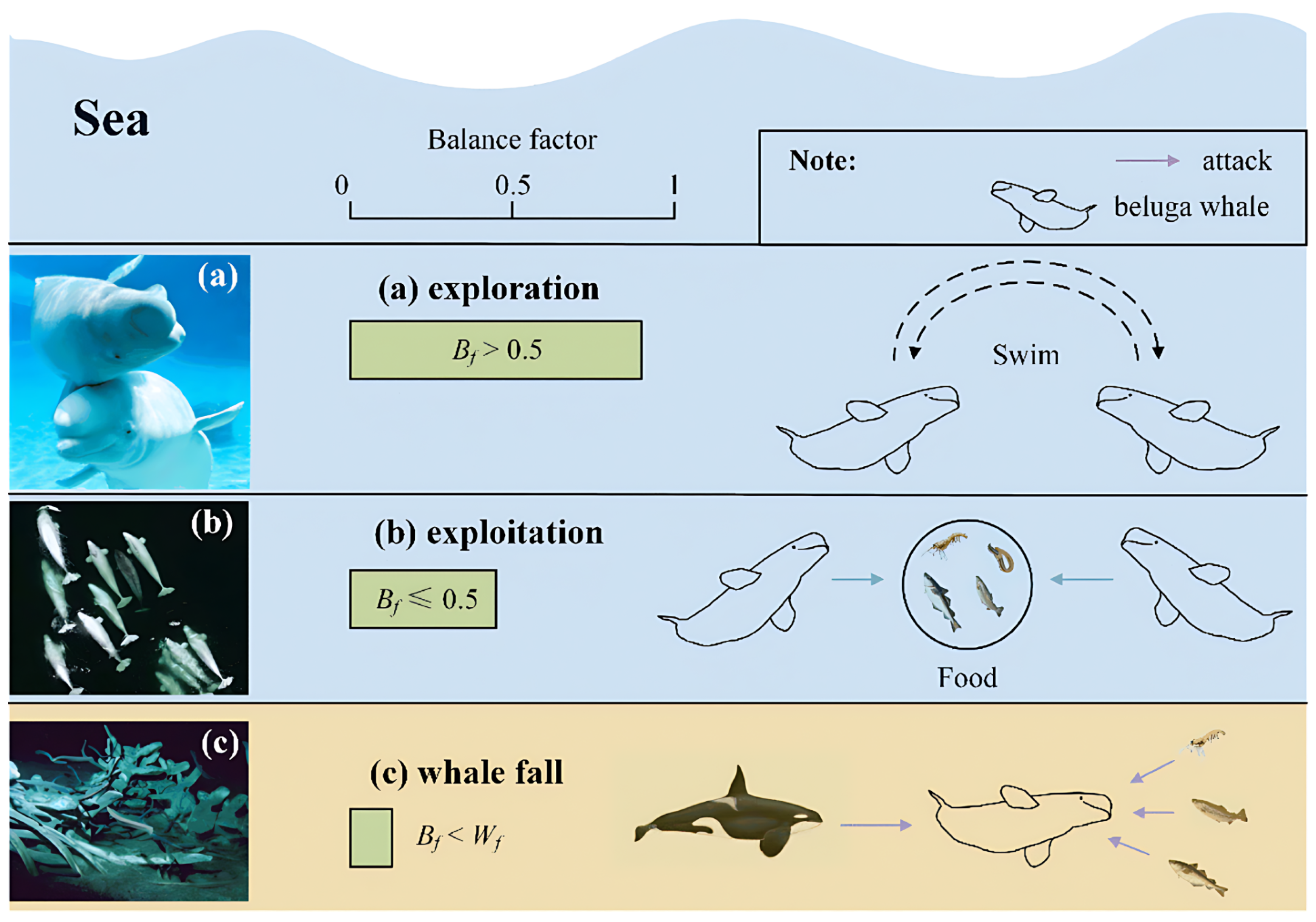
Chaotic map	Improved Circle map

summarises the key hyperparameters used in the proposed Multi-Strategy Beluga Whale Optimization (MSBWO) algorithm. These parameters include the population size, maximum iterations for both PID and FOPID tuning, and the specific values for the Lévy flight index $\beta$, whale fall probability $W_f$, and spiral control factor b. Additionally, the table lists the elite pool size, which is set to the top 3 candidates plus a weighted average, and the chaotic map used for initialisation, which is the improved Circle map. These hyperparameters were carefully chosen to balance exploration and exploitation in the optimisation process, contributing to the algorithm’s performance.

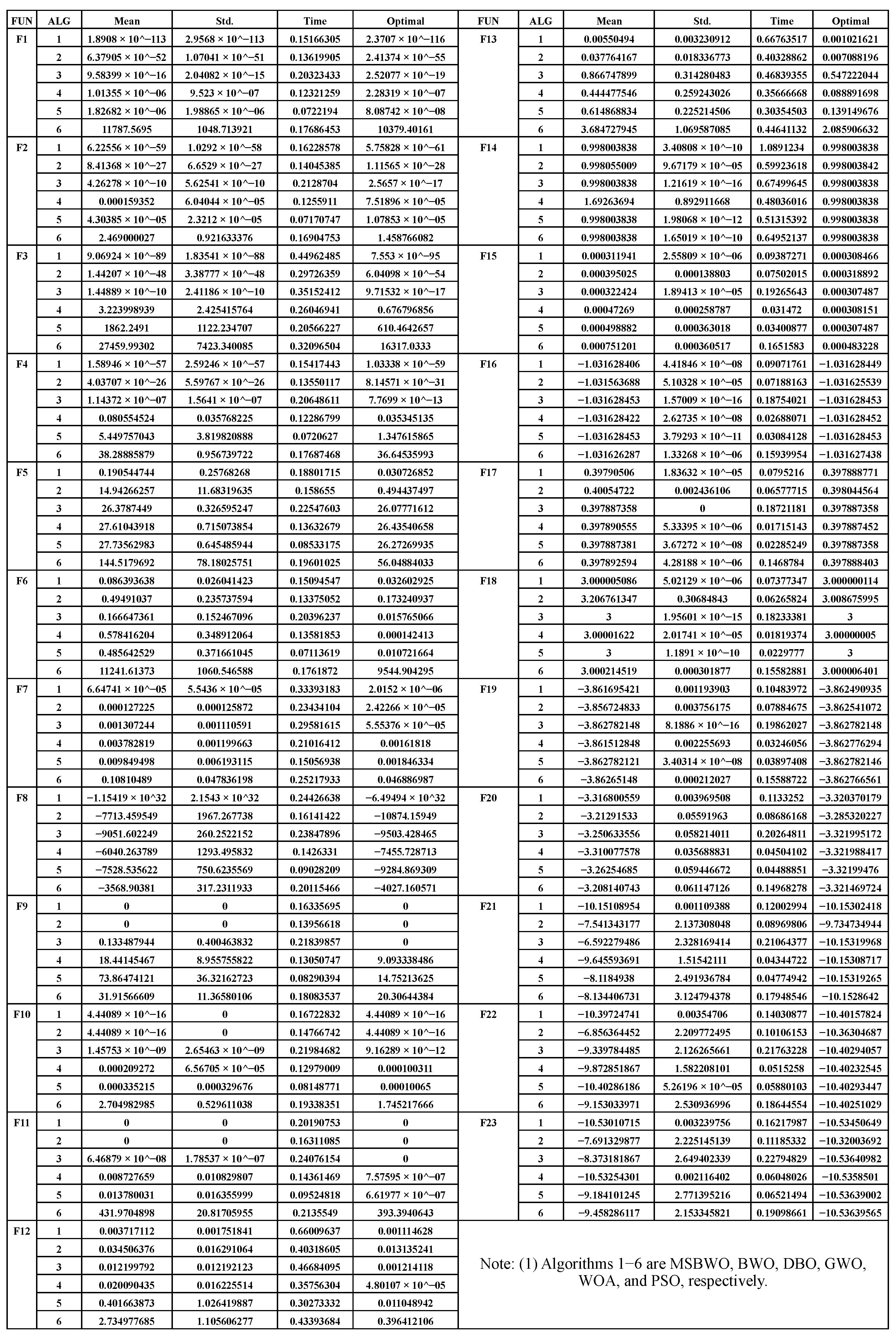
Figure 9 illustrates the convergence performance of the compared algorithms across the 23 test functions. In terms of convergence speed, the MSBWO algorithm demonstrates superior performance in most cases (e.g., F1, F2, F3, F4, F6, F10, F12). Although PSO and WOA exhibit competitive convergence rates on functions such as F7, F8, and F14, they generally lag behind MSBWO. Regarding global optimum accuracy, MSBWO achieves high precision on functions including F1, F2, F3, F4, F8, F10, and F12. While other algorithms like BWO and GWO show good performance on certain benchmarks, their effectiveness is not as widespread. In terms of stability, MSBWO consistently approaches the global optimum across most test functions. Although GWO and PSO display robustness on selected cases, their overall consistency remains inferior to MSBWO.

Based on this comprehensive evaluation, MSBWO exhibits the best overall performance among the tested algorithms, excelling in convergence speed, global accuracy, and solution stability.

Figure 10 presents box plots comparing the fitness distribution of the optimisation algorithms across the same 23 benchmark functions. The results reveal varying algorithmic performances. For instance, on functions F1, F3, F4, F5, F6, F7, F9, F10, F11, F12, F13, F15, and F18, PSO yields significantly higher fitness values, suggesting subpar performance. In contrast, MSBWO, along with BWO, DBO, GWO, and WOA, generally achieves lower and more stable fitness results on these benchmarks. On F2, all algorithms show relatively low fitness values, indicating limited difficulty. On F14, DBO performs the worst, while others maintain acceptable fitness. For F16, F17, F19, and F20, MSBWO again achieves the best performance with the lowest fitness values, followed by GWO, DBO, and WOA, while PSO continues to underperform.

In summary, MSBWO delivers superior performance on most benchmark functions in the CEC2005 suite, outperforming other algorithms in terms of accuracy and consistency. These results suggest that MSBWO is well-suited for similar complex optimisation problems. Conversely, PSO demonstrates limitations and may require enhancements or replacement with more effective methods in these scenarios. For detailed numerical results, please refer to Appendix Figure A1.

5.2. Performance of the TWSBR Control System

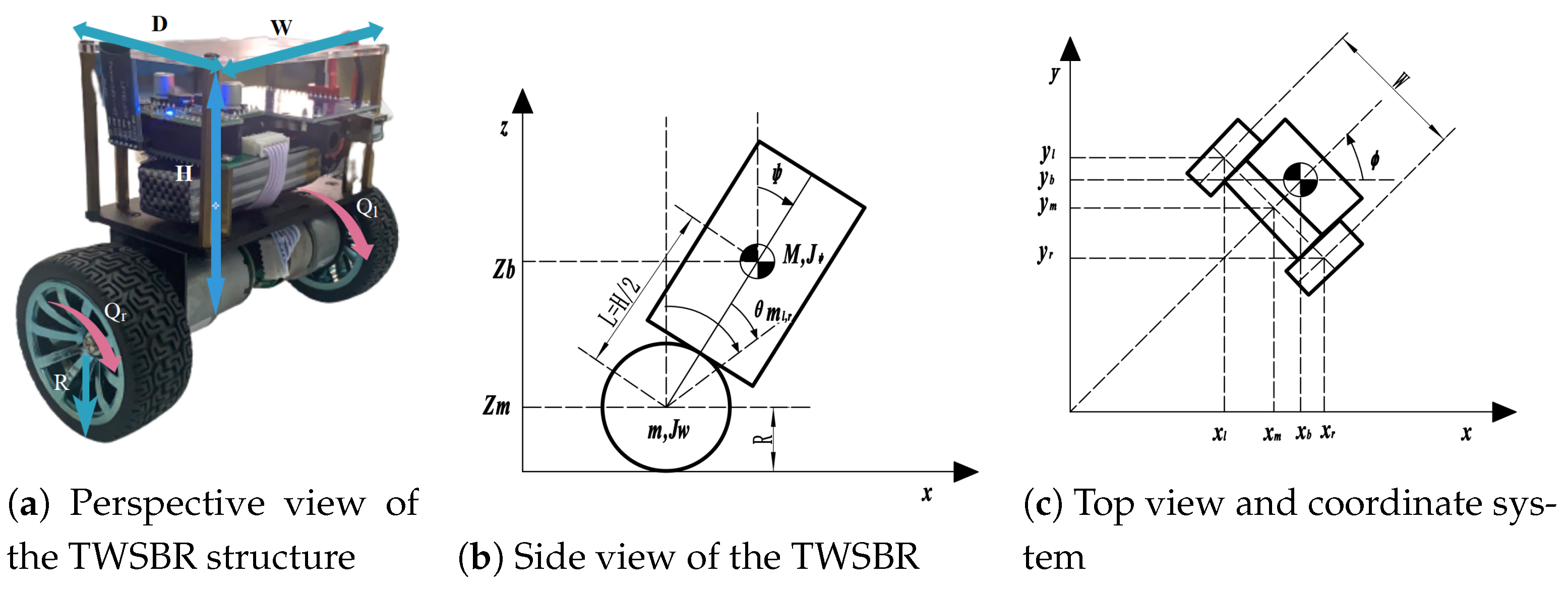
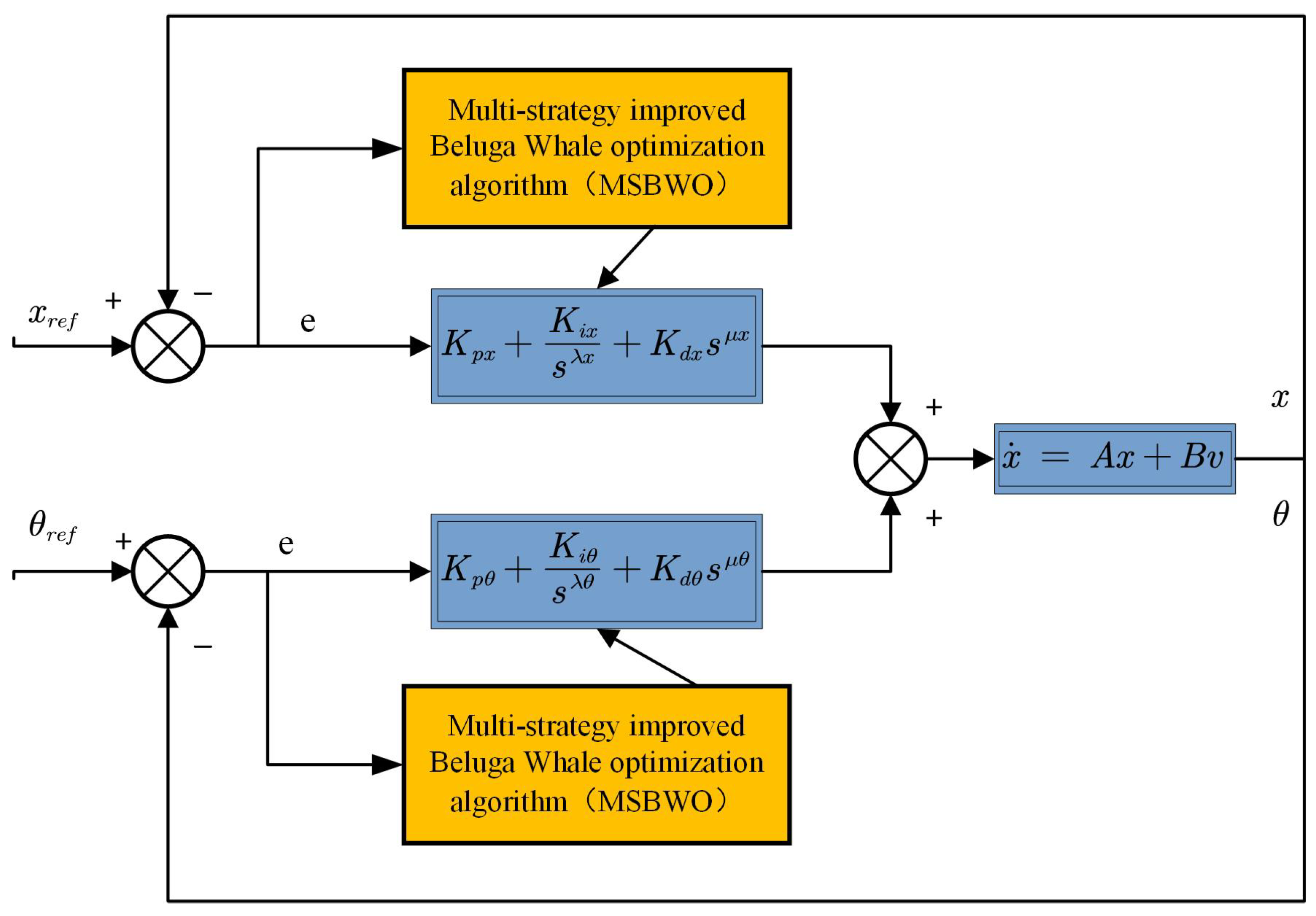
In this study, a TWSBR model with integrated DC motor dynamics was developed, and both FOPID and traditional integer-order PID controllers were designed for balance and position control. Notably, when the FOPID parameters $\lambda =\mu =1$, the controller reduces to a classic PID. The overall control structure is illustrated in Figure 11, where two independent controllers are responsible for regulating the position (X) and tilt angle ($\theta$), respectively. However, since both controllers function similarly, this analysis focuses on tilt angle ($\theta$) regulation, which is critical to the robot’s balance.

The control input is derived from the difference between the two controller outputs. The input to the physical system, modelled as a DC motor, is voltage. All simulations and controller optimisations were implemented in MATLAB 2023b with a sampling interval of ${10}^{-3}$ seconds. A step disturbance of 0.2 amplitude was applied at $t=1$ s, and the reference angle was set to $0°$. The system dynamics follow the state-space model defined in Equation (66).

Table 3. Notation used in the dynamic modelling and control design.

Symbol	Description
$\theta$	Body tilt angle of the robot (pitch angle)
X	Wheel position
$K_p,K_i,K_d$	PID controller parameters
$\lambda ,\mu$	Fractional integral and derivative orders of FOPID
$0°$	Reference tilt angle (setpoint)
$0.2$	Step disturbance amplitude applied at $t=1$ s
${10}^{-3}$ s	Sampling interval used in simulations
V	Voltage input to the DC motor (control input)
$u_1$	Control input for forward motion ($v_l+v_r$)
$u_2$	Control input for yaw motion ($v_l-v_r$)

summarises the key notations used in the dynamic modelling and control design of the two-wheeled self-balancing robot (TWSBR).

The FOPID controller has five tunable parameters, in contrast to the three of the conventional PID controller. Proper tuning is critical to ensure fast settling time, minimal overshoot, and low angular fluctuation in $\theta$. To determine optimal parameters, six metaheuristic algorithms were applied: PSO, WOA, DBO, GWO, BWO, and MSBWO. Both PID and FOPID controllers were optimised using each algorithm and evaluated based on their system response and overall output error.

For the PID controller, each algorithm employed a population size of 30 and 200 iterations. For the more complex FOPID, the population size was 30 with 400 iterations to accommodate the increased search space. These settings were chosen empirically to balance performance and computational efficiency. Parameter bounds were $[0,{10}^6]$ for $K_p$, $K_i$, and $K_d$ (PID), and $[0,{10}^5]$ for $K_p$, $K_i$, $K_d$, $\lambda$, and $\mu$ (FOPID).

Controller tuning was guided by standard performance metrics: IAE, ISE, ITAE, and ITSE:

$$\begin{array}{cc}\hfill & \mathrm{IAE}={\int }_0^{\infty }\left|e\left(t\right)\right|dt,\mathrm{ISE}={\int }_0^{\infty }{e}^2\left(t\right)dt,\hfill \\ \hfill & ITAE={\int }_0^{\infty }t\left|e\left(t\right)\right|dt,\mathrm{ITSE}={\int }_0^{\infty }t{e}^2\left(t\right)dt\hfill \end{array}$$

(67)

Various objective functions combining these metrics were tested, including weighted sums incorporating overshoot and peak velocity. Coefficients were chosen via empirical tuning:

$$\begin{array}{cc}\hfill & f_1={\mathrm{ITAE}}_{\theta },\hfill \\ \hfill & f_2={\mathrm{IAE}}_{\theta }+{\mathrm{ITAE}}_{\theta },\hfill \\ \hfill & f_3={\mathrm{IAE}}_{\theta }+{\mathrm{ITAE}}_{\theta }+{\mathrm{ISE}}_{\theta }+{\mathrm{ITSE}}_{\theta },\hfill \\ \hfill & f_4={100}^2{\mathrm{IAE}}_{\theta }+{100}^2{\mathrm{ITAE}}_{\theta }+{10}^{2}O{S}_{\theta }+{10}^{2}max\left(\dot{\theta }\right)\hfill \end{array}$$

(68)

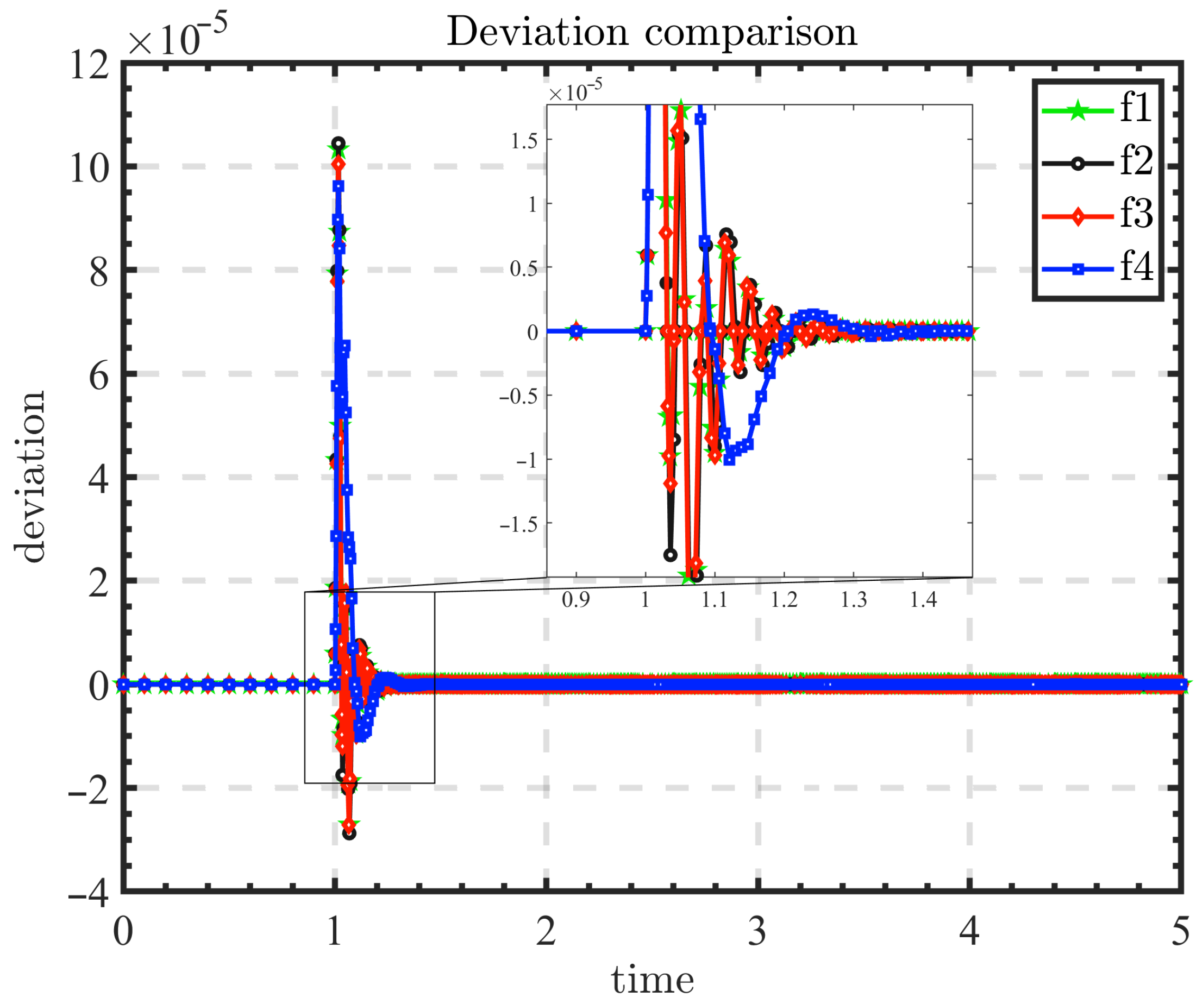
Figure 12 shows that the objective function $f_4$ achieves the best performance in terms of both convergence and stability. Specifically, it converges rapidly to a near-zero value and maintains a consistently low deviation, even in the presence of initial oscillations. The robustness of $f_4$ is evident, as it consistently outperforms other objective functions in reducing the steady-state error while minimizing overshoot. Consequently, $f_4$ was selected as the preferred objective function for controller parameter optimisation in this study due to its superior performance in terms of both convergence speed and steady-state accuracy. As illustrated in Figure 13, the fitness values demonstrate iterative convergence when optimising with different objective functions. Among them, $f_4$ achieves the most stable and rapid convergence, further confirming its effectiveness for controller parameter optimisation.

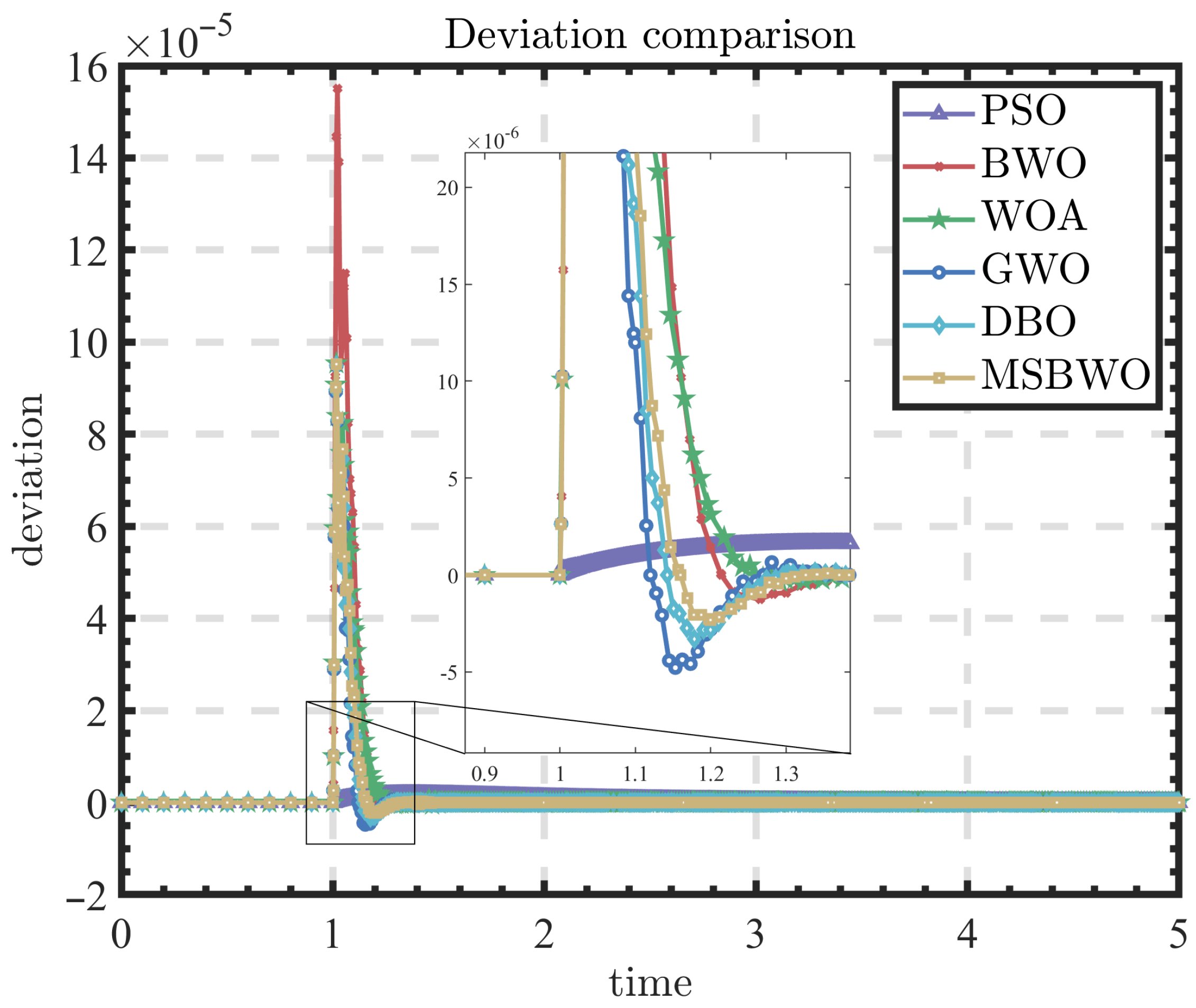
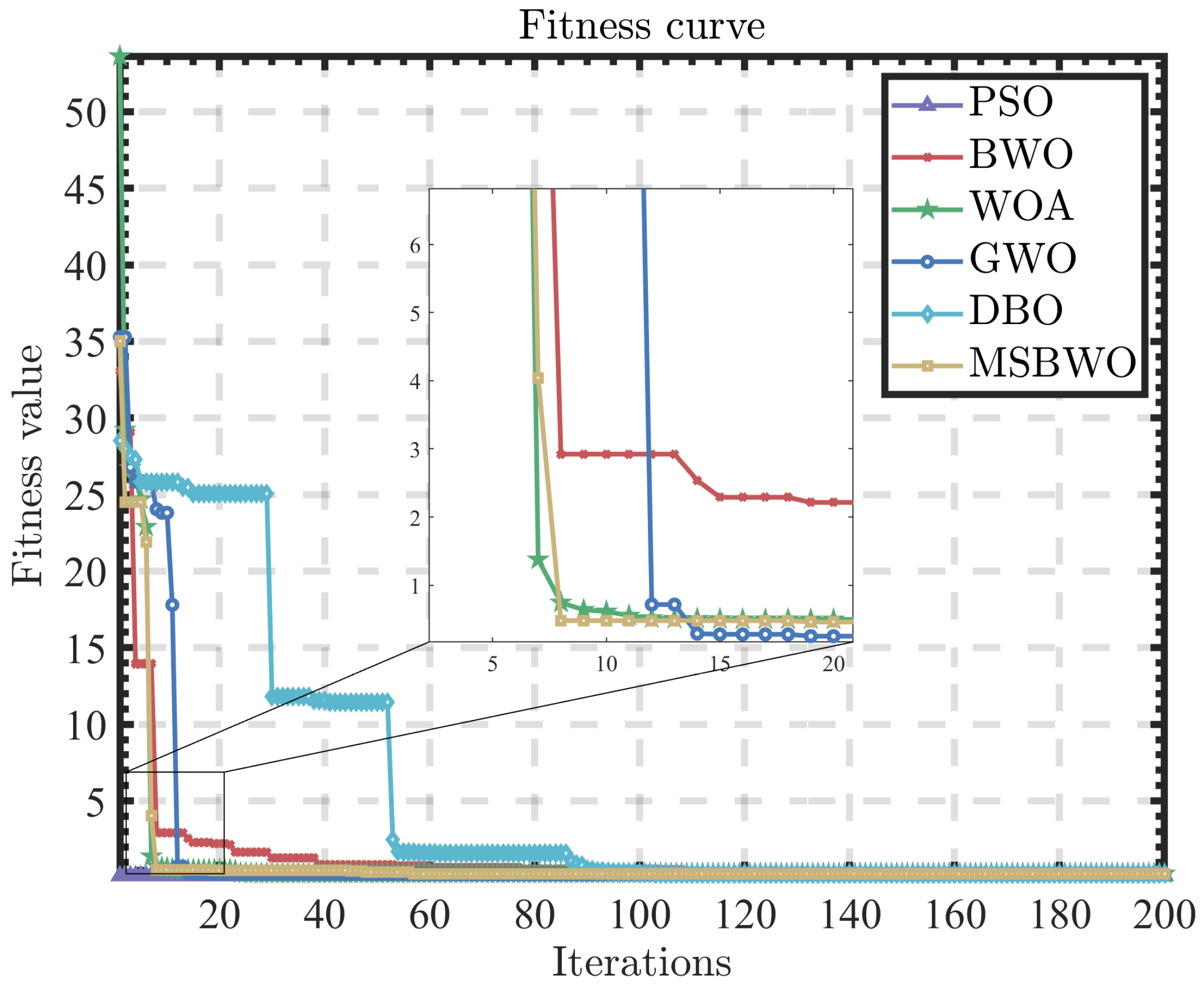
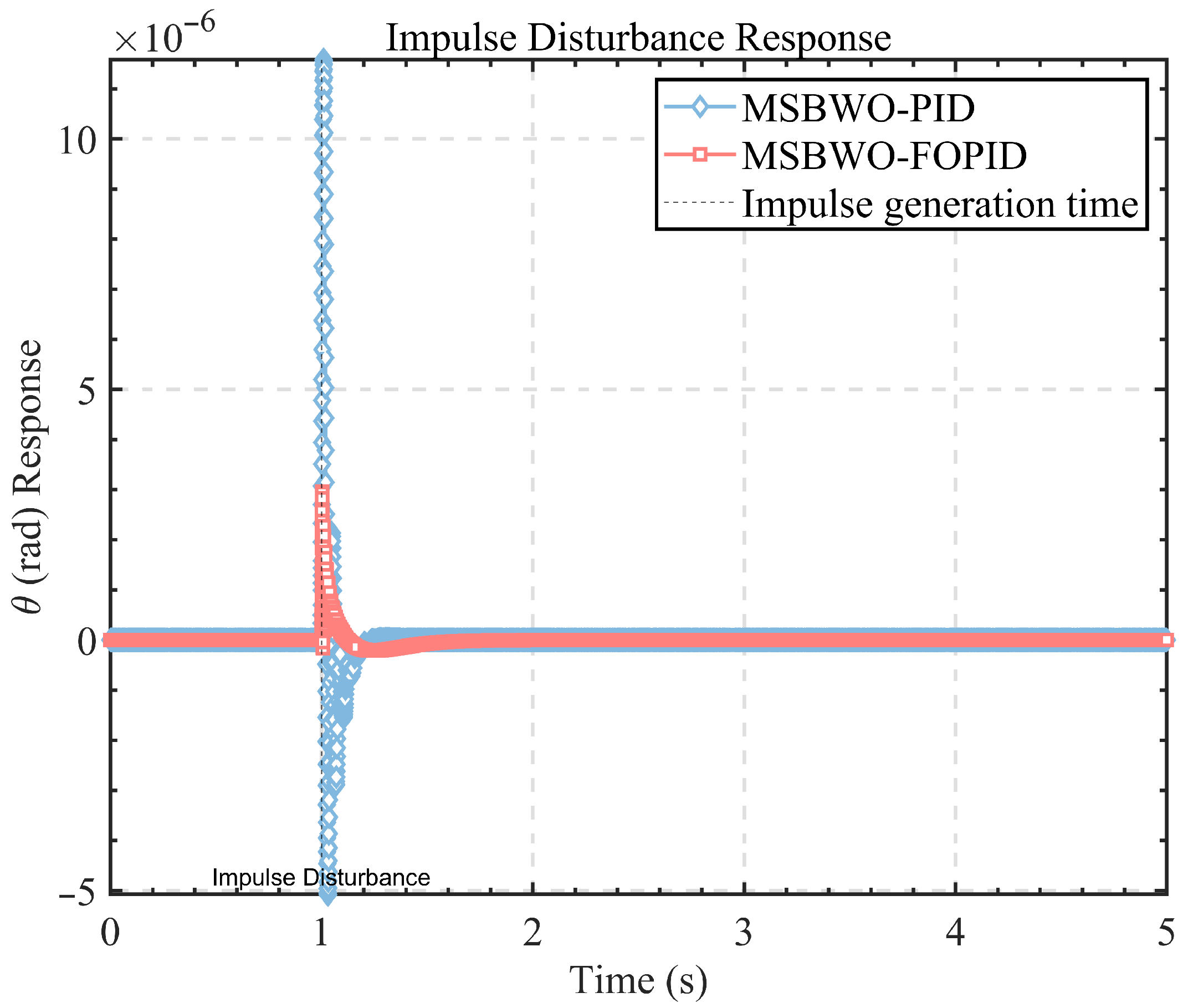
By analysing the variation in system deviation over time (Figure 14) and the evolution of fitness values over iterations (Figure 15), a detailed comparative analysis was conducted for each algorithm based on key performance indicators, including overshoot, convergence time, and steady-state error.

Figure 14 shows that the MSBWO-PID algorithm demonstrated the best performance, exhibiting the smallest overshoot, the shortest convergence time, and rapid attainment of zero steady-state error. In contrast, the PSO-PID algorithm failed to converge properly, resulting in significant errors. Consequently,

Table 4. Objective function value and iteration numbers for various PID control strategies.

Controller	Objective Values	Iteration Numbers
PSO-PID	–	–
BWO-PID	0.3723	109
WOA-PID	0.2556	24
GWO-PID	0.2349	14
DBO-PID	0.2347	103
MSBWO-PID	0.2389	57

does not report its target value or iteration count. The GWO-PID algorithm exhibited relatively large overshoot and extended convergence time, while the BWO-PID and WOA-PID algorithms experienced large initial fluctuations and convergence times comparable to GWO. Among all, the DBO-PID algorithm yielded the poorest performance, with the largest overshoot and the slowest convergence.

Figure 15 shows that the MSBWO-PID algorithm again achieved superior results. It displayed the fastest initial decline within the first 20 iterations and reached the lowest final fitness value, approaching zero. In contrast, the PSO-PID, BWO-PID, WOA-PID, and GWO-PID algorithms showed slower convergence and higher final fitness values. The DBO-PID algorithm exhibited the slowest convergence and the highest final fitness value.

In summary, the MSBWO-PID algorithm outperformed all other methods in tuning the PID controller parameters for the TWSBR. It achieved minimal overshoot, the fastest convergence, the lowest steady-state error, the steepest initial fitness decline, and the lowest final fitness value. Conversely, the other algorithms suffered from varying degrees of fluctuation, significant overshoot, and sluggish convergence. Therefore, the MSBWO-PID algorithm is validated as the most effective approach for PID parameter optimisation in TWSBR applications.

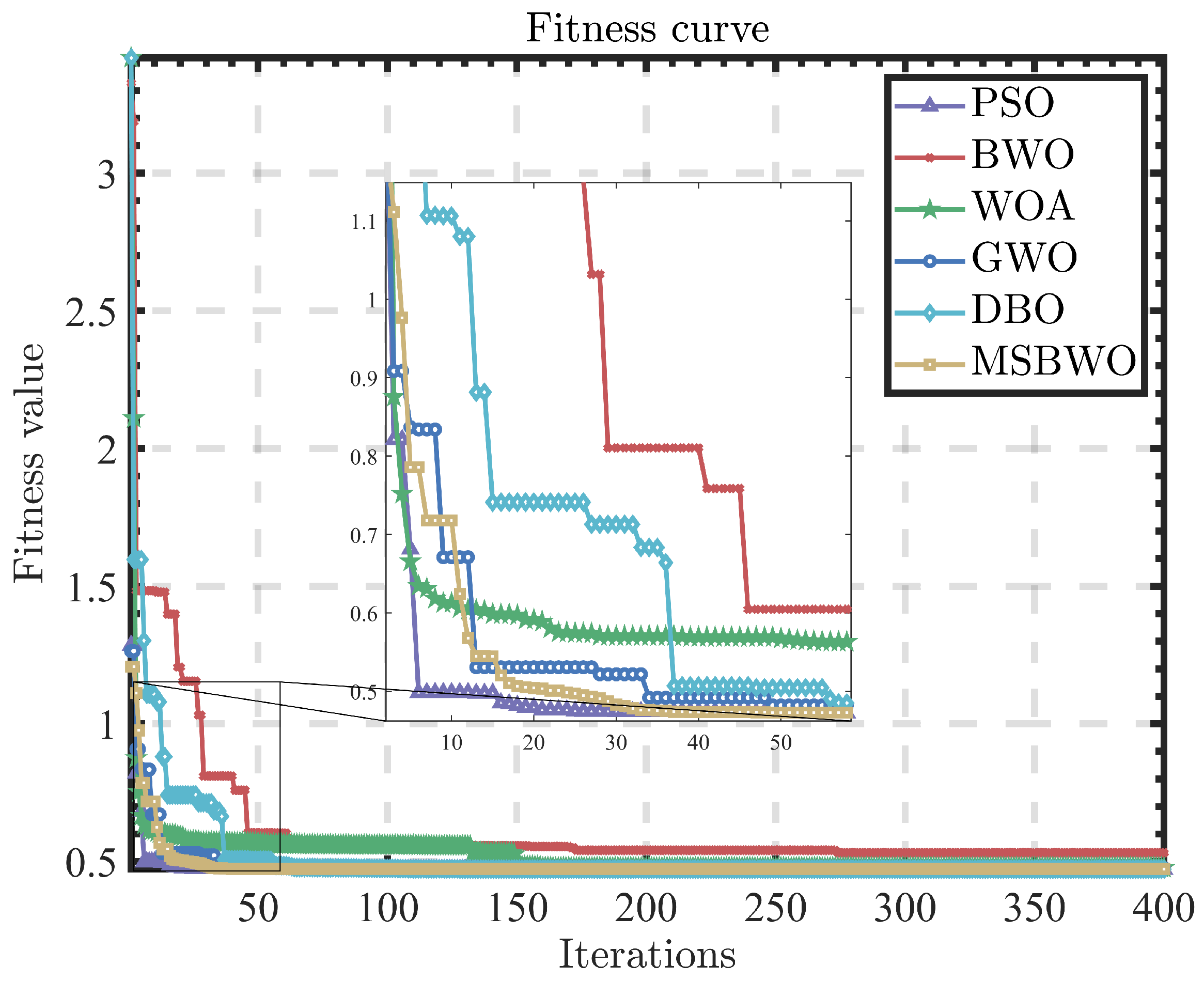
By analysing the deviation of the system over time (Figure 16) and the evolution of the fitness value across iterations (Figure 17), a detailed comparison was conducted among the algorithms based on key indicators such as overshoot, convergence time, and steady-state error. The results of TWSBR FOPID parameter tuning show that the MSBWO-FOPID algorithm outperforms the others in terms of convergence speed, control stability, and optimal fitness value. Specifically, it achieves the fastest convergence and the smallest deviation.

Figure 16 shows that the MSBWO-FOPID algorithm exhibits the lowest overshoot and the shortest steady-state time. The deviation decreases rapidly and stabilises within approximately one second, which is significantly faster than the other algorithms. In contrast, the BWO-FOPID and WOA-FOPID algorithms show slower convergence and longer settling times, while the GWO-FOPID and DBO-FOPID algorithms display moderate convergence and stabilisation performance.

Figure 17 shows that the MSBWO-FOPID algorithm again demonstrates superior performance, with its fitness value decreasing rapidly and stabilising after approximately 50 iterations, reflecting strong optimisation capability and fast convergence. Although the PSO-FOPID and DBO-FOPID algorithms also exhibit relatively fast convergence, their fitness fluctuations are minimal. Meanwhile, the BWO-FOPID and WOA-FOPID algorithms display significant fluctuations and slower convergence.

In summary, the MSBWO-FOPID algorithm achieves the best overall performance in terms of overshoot, steady-state time, convergence speed, and fitness value. Therefore, it is recommended as the preferred method for optimising FOPID parameters in TWSBR control applications.

Table 4 and

Table 5. Objective function values and iteration numbers for FOPID controllers.

Controller	Objective Values	Iteration Numbers
PSO-FOPID	0.4716	50
BWO-FOPID	0.5313	274
WOA-FOPID	0.4772	151
GWO-FOPID	0.4776	113
DBO-FOPID	0.4716	63
MSBWO-FOPID	0.4726	36

present the objective function values and iteration counts for PID and FOPID control, respectively. In Table 4, the performance of each optimisation algorithm for PID control is summarised. GWO-PID and DBO-PID achieve the lowest objective values of 0.2349 and 0.2347, respectively, with GWO-PID requiring only 14 iterations, indicating the fastest convergence. However, as shown in Figure 14, both GWO-PID and DBO-PID exhibit substantial overshoot. The MSBWO-PID algorithm also demonstrates strong overall performance, achieving an objective value of 0.2389 within 57 iterations, reflecting a good balance between accuracy and convergence.

In Table 5, the FOPID control results indicate that MSBWO-FOPID outperforms other algorithms, achieving the lowest objective value of 0.4726 with only 36 iterations. This highlights the MSBWO algorithm’s effectiveness in tuning FOPID controllers, enabling rapid convergence with fewer iterations.

Table 6. Performance evaluation indicators for PID controllers.

Controller	IAE	ITAE	ISE	ITSE	OS.	ST.
PSO-PID	$2.085\times {10}^{-6}$	$4.109\times {10}^{-6}$	$2.178\times {10}^{-12}$	$3.621\times {10}^{-12}$	$1.628\times {10}^{-6}$	4.000
BWO-PID	$1.128\times {10}^{-5}$	$1.207\times {10}^{-5}$	$1.026\times {10}^{-9}$	$1.075\times {10}^{-9}$	$1.550\times {10}^{-4}$	0.616
WOA-PID	$7.545\times {10}^{-6}$	$8.136\times {10}^{-6}$	$4.169\times {10}^{-10}$	$4.374\times {10}^{-10}$	$9.538\times {10}^{-5}$	0.531
GWO-PID	$5.150\times {10}^{-6}$	$5.445\times {10}^{-6}$	$2.773\times {10}^{-10}$	$2.871\times {10}^{-10}$	$9.491\times {10}^{-5}$	0.519
DBO-PID	$5.588\times {10}^{-6}$	$5.933\times {10}^{-6}$	$3.056\times {10}^{-10}$	$3.172\times {10}^{-10}$	$9.500\times {10}^{-5}$	0.401
MSBWO-PID	$5.926\times {10}^{-6}$	$6.286\times {10}^{-6}$	$3.274\times {10}^{-10}$	$3.405\times {10}^{-10}$	$9.521\times {10}^{-5}$	0.319

and

Table 7. Performance evaluation indicators for FOPID controllers.

Controller	IAE	ITAE	ISE	ITSE	OS.	ST.
PSO-FOPID	$1.998\times {10}^{-5}$	$2.440\times {10}^{-5}$	$9.077\times {10}^{-10}$	$1.066\times {10}^{-9}$	$6.494\times {10}^{-5}$	0.950
BWO-FOPID	$1.821\times {10}^{-5}$	$3.222\times {10}^{-5}$	$2.066\times {10}^{-10}$	$2.978\times {10}^{-10}$	$2.333\times {10}^{-5}$	2.500
WOA-FOPID	$2.004\times {10}^{-5}$	$2.579\times {10}^{-5}$	$6.799\times {10}^{-10}$	$7.981\times {10}^{-10}$	$2.333\times {10}^{-5}$	1.478
GWO-FOPID	$2.002\times {10}^{-5}$	$2.478\times {10}^{-5}$	$8.295\times {10}^{-10}$	$9.449\times {10}^{-10}$	$6.905\times {10}^{-5}$	1.252
DBO-FOPID	$1.998\times {10}^{-5}$	$2.447\times {10}^{-5}$	$8.935\times {10}^{-10}$	$1.050\times {10}^{-9}$	$6.425\times {10}^{-5}$	0.948
MSBWO-FOPID	$1.998\times {10}^{-5}$	$2.423\times {10}^{-5}$	$9.416\times {10}^{-10}$	$1.092\times {10}^{-9}$	$6.896\times {10}^{-5}$	0.852

report detailed performance indicators for PID and FOPID controllers. According to Table 6, PSO-PID performs best in terms of IAE, ITAE, ISE, and ITSE. However, it lacks convergence characteristics and requires the longest time to reach steady state. In contrast, GWO-PID and MSBWO-PID are superior in overshoot (OS) and steady-state time (ST), with MSBWO-PID achieving the shortest ST of just 0.319 s, demonstrating rapid dynamic response.

For FOPID control, Table 7 shows that although BWO-FOPID performs well in IAE, ITAE, ISE, and ITSE, its stabilisation time is excessively long, as also evidenced in Figure 16. The MSBWO-FOPID algorithm achieves the lowest overshoot ($6.896\times {10}^{-5}$) and shortest steady-state time (0.852 s), further confirming its superior performance.

Table 8. Controller parameters for PID controllers.

Controller	${\mathbf{K}}_{\mathbf{p}}$	${\mathbf{K}}_{\mathbf{d}}$	${\mathbf{K}}_{\mathbf{i}}$
PSO-PID	95,751	95,022	14,929
BWO-PID	1080	18,204	22
WOA-PID	1766	26,873	33
GWO-PID	1532	44,979	36
DBO-PID	1605	39,492	35
MSBWO-PID	1641	36,266	34

and

Table 9. Controller parameters for FOPID controllers.

Controller	${\mathbf{K}}_{\mathbf{p}}$	${\mathbf{K}}_{\mathbf{d}}$	${\mathbf{K}}_{\mathbf{i}}$	$\mathit{\lambda }$	$\mathit{\mu }$
PSO-FOPID	2224	9999	137	1.0001	1.0126
BWO-FOPID	10,000	9921	7	1.1025	1.3628
WOA-FOPID	2813	9999	125	1.0000	0.7891
GWO-FOPID	2369	10,000	26	1.0001	0.8583
DBO-FOPID	2250	9999	139	1.0001	1.0083
MSBWO-FOPID	2123	10,000	114	1.0000	0.9982

list the controller parameter values for PID and FOPID controllers, respectively, under different optimisation algorithms.

The numerical results in Table 4 and Table 5 present the objective function values for PID and FOPID controllers, respectively. These values are meaningful only within the same controller category (i.e., PID vs. PID, or FOPID vs. FOPID). Direct cross-comparison between Table 4 and Table 5 is inappropriate, as the inclusion of fractional orders $(\lambda ,\mu )$ in the FOPID introduces additional design flexibility, primarily enhancing robustness and frequency-domain characteristics rather than minimising the time-domain aggregated objective. Similarly, the error-based indicators in Table 6 and Table 7 (IAE, ITAE, ISE, ITSE) are intended for intra-category evaluation and should be interpreted within this context.

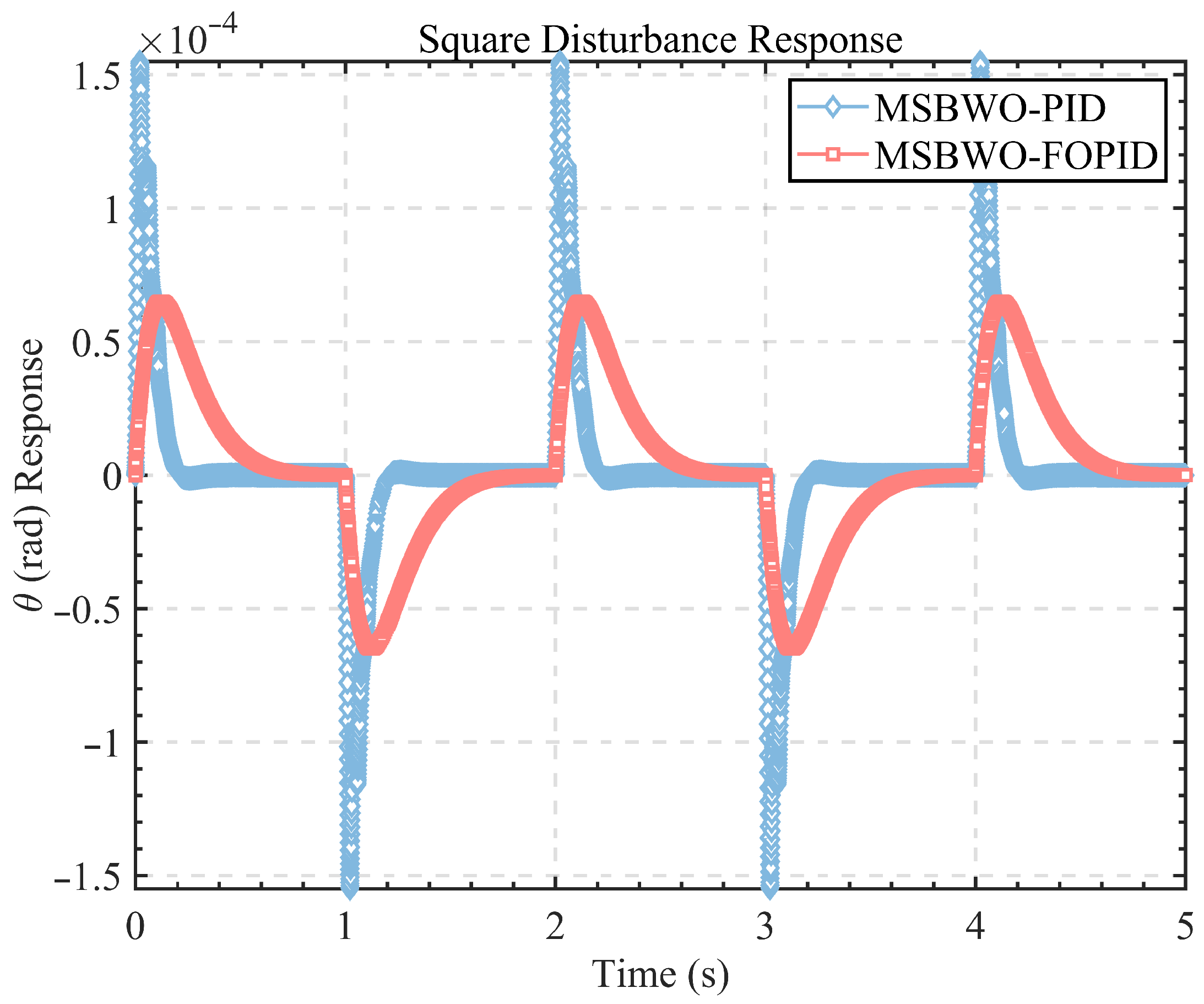
In the performance comparison, we focus on transient metrics such as overshoot (OS) and settling time (ST), as well as system responses shown in Figure 14 and Figure 16. For instance, Table 6 indicates that the best PID design (MSBWO-PID) achieves a settling time of $0.319$ s but suffers from an overshoot of $9.521\times {10}^{-5}$. In contrast, Table 7 and Figure 16 show that the MSBWO-FOPID achieves the lowest overshoot ($6.896\times {10}^{-5}$) and smooth recovery, confirming its superior robustness and dynamic stability. The trajectory responses in Figure 14 and Figure 16 further highlight that FOPID controllers, when optimised by MSBWO, exhibit faster damping of deviations and more reliable disturbance rejection. Although the FOPID controller may require slightly more time to reach steady state, it maintains smaller deviation fluctuations and greater stability, particularly in dynamic and disturbed environments.

In conclusion, the integration of the FOPID controller with the MSBWO optimisation algorithm results in significant improvements in control accuracy, stability, and robustness, making it highly suitable for complex systems with stringent performance requirements. While the conventional PID controller demonstrates strong performance, the FOPID controller, particularly when optimised using the MSBWO algorithm, offers substantial advantages in deviation suppression, convergence speed, and overall optimisation effectiveness.

5.3. Disturbance Rejection Analysis

In addition to the step response analysis discussed above, three disturbance scenarios were further investigated to comprehensively assess the robustness of the proposed controllers. Specifically, random noise, square-wave, and impulse disturbances were introduced into the system, and the corresponding responses are presented in Figure 18, Figure 19 and Figure 20. These disturbance tests provide deeper insights into the resilience of the MSBWO-PID and MSBWO-FOPID controllers under different types of external perturbations.

Under random noise disturbance (Figure 18), the MSBWO-PID controller exhibits significant oscillations and sensitivity to high-frequency fluctuations. In contrast, the MSBWO-FOPID controller demonstrates a smoother response with smaller amplitude deviations, indicating superior noise attenuation capability. This implies that the fractional-order parameters provide additional flexibility in shaping the frequency response, thereby enhancing robustness against stochastic disturbances.

For the square-wave disturbance (Figure 19), both controllers are able to track the disturbance changes; however, the MSBWO-FOPID yields smaller overshoot and faster recovery after each switching instant. This highlights its advantage in handling abrupt external perturbations while maintaining system stability.

In the case of the impulse disturbance (Figure 20), introduced at $t=1$ s, the MSBWO-PID controller suffers from a large instantaneous deviation, whereas the MSBWO-FOPID significantly reduces the peak response and achieves faster settling to the equilibrium state. The enhanced transient suppression clearly reflects the improved robustness and disturbance rejection property of the fractional-order controller.

Overall, the comparative analysis demonstrates that the MSBWO-FOPID controller consistently outperforms the MSBWO-PID controller under all tested disturbance conditions. The results validate the effectiveness of integrating fractional-order dynamics with the multi-strategy Beluga Whale Optimisation algorithm for achieving resilient and stable control of nonlinear robotic systems.

6. Conclusions

The results of this study indicate that the proposed MSBWO algorithm exhibits superior performance in optimising FOPID parameters for two-wheeled self-balancing robots (TWSBRs). Compared with other optimisation algorithms, MSBWO consistently achieves faster convergence, improved stability, and better fitness values. In particular, it delivers the smallest deviation, reduced overshoot, and shorter steady-state time, confirming its effectiveness in enhancing dynamic response. Furthermore, the FOPID controller tuned by MSBWO consistently outperforms its integer-order PID counterpart, thereby reaffirming the advantages of incorporating fractional-order parameters $(\lambda ,\mu )$ in control system design.

Therefore, the MSBWO algorithm can be recommended as an effective and robust method for tuning FOPID controllers in TWSBR applications. Nevertheless, this study has been limited to simulation-based validation. As future work, we plan to extend the framework to hardware-in-the-loop testing and experimental implementation on a physical TWSBR platform, in order to further demonstrate practical feasibility and real-world performance. In addition, we will investigate the ISO-dampingproperty as a frequency-domain robustness criterion, which will complement the present time-domain disturbance analyses and provide a more comprehensive evaluation of system stability.