Exploring Solitons Solutions of a (3+1)-Dimensional Fractional mKdV-ZK Equation
Abstract
1. Introduction
2. Methodology
| Sr. No. | ||||
| 1 | 1 | or | ||
| 2 | ||||
| 3 | −1 | |||
| 4 | 1 | or | ||
| 5 | ||||
| 6 | −1 | |||
| 7 | 1 | |||
| 8 | 1 | |||
| 9 | 1 | |||
| 10 | 1 | |||
| 11 | or | |||
| 12 | ||||
| 13 | ||||
| 14 |
| function | function | ||||
| 1 | 1 | ||||
| 1 | 1 | ||||
3. Implementation of the Expansion Method
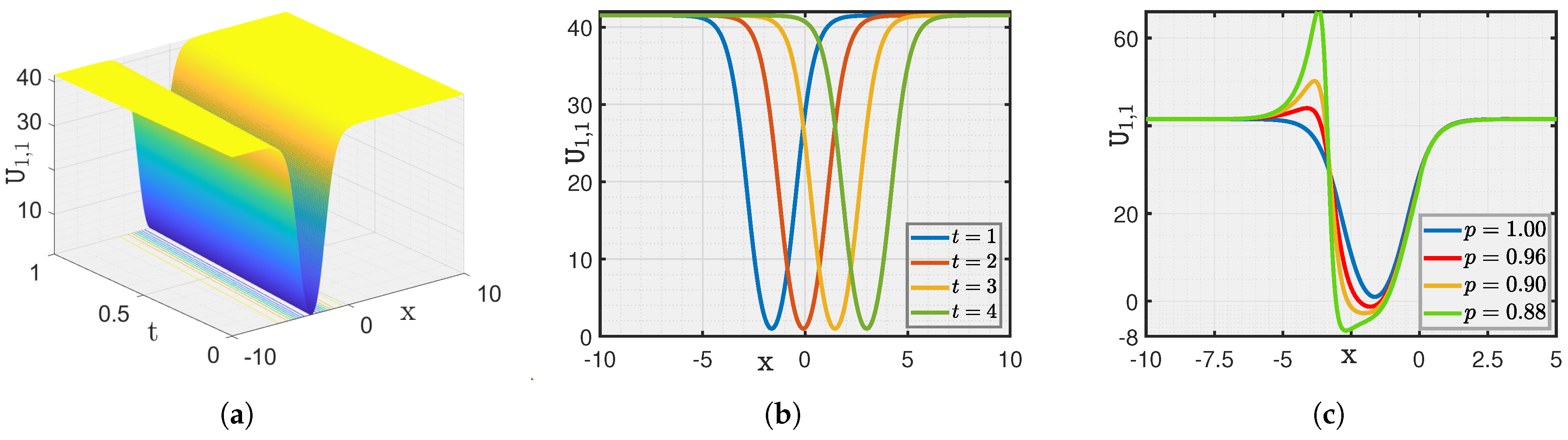
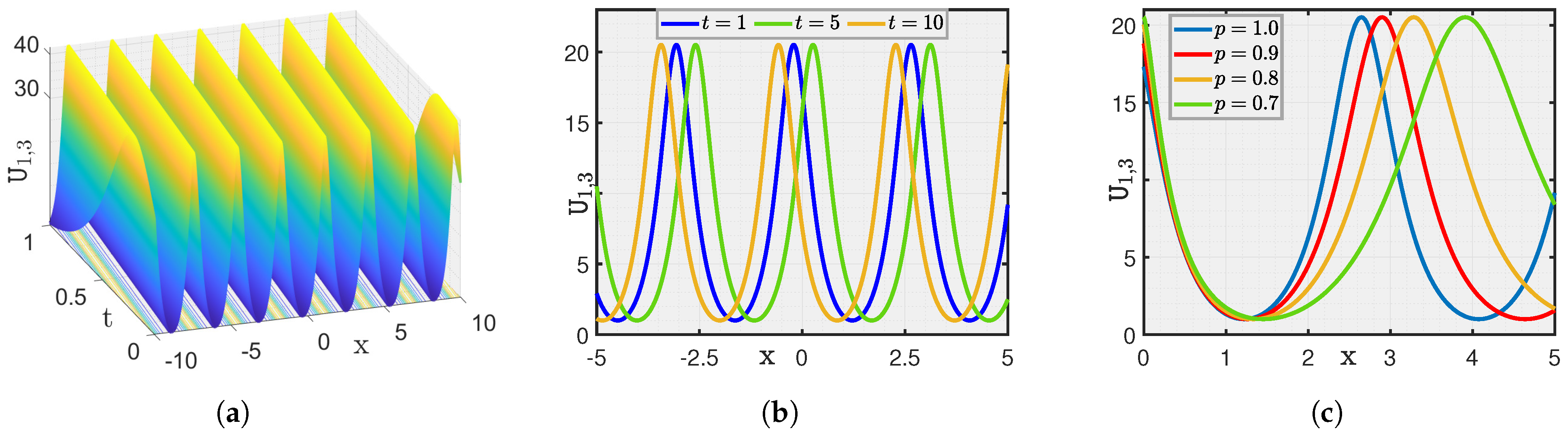
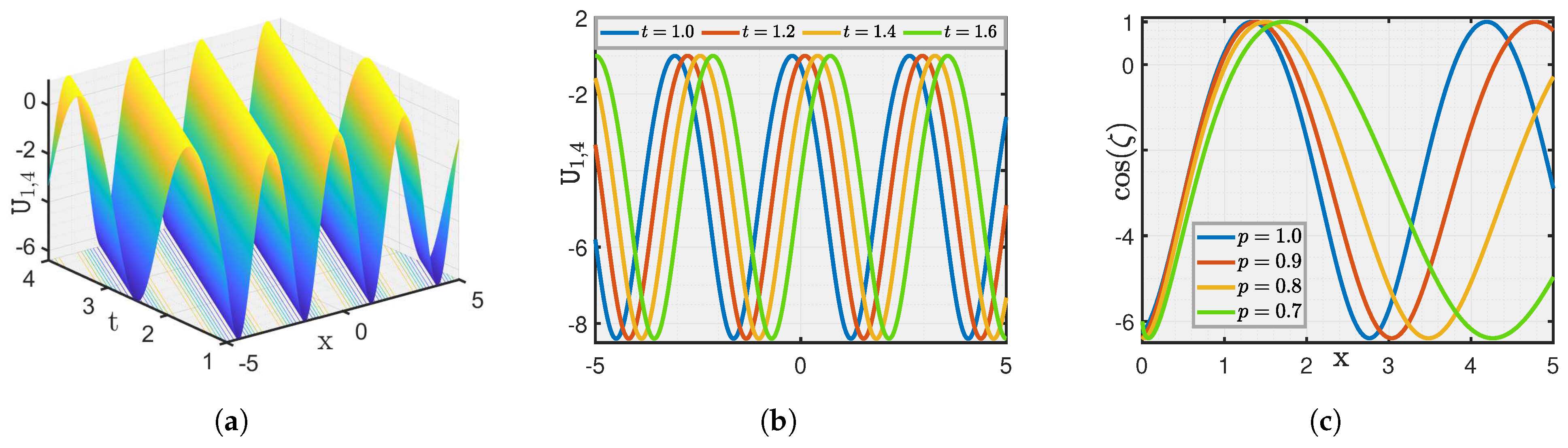
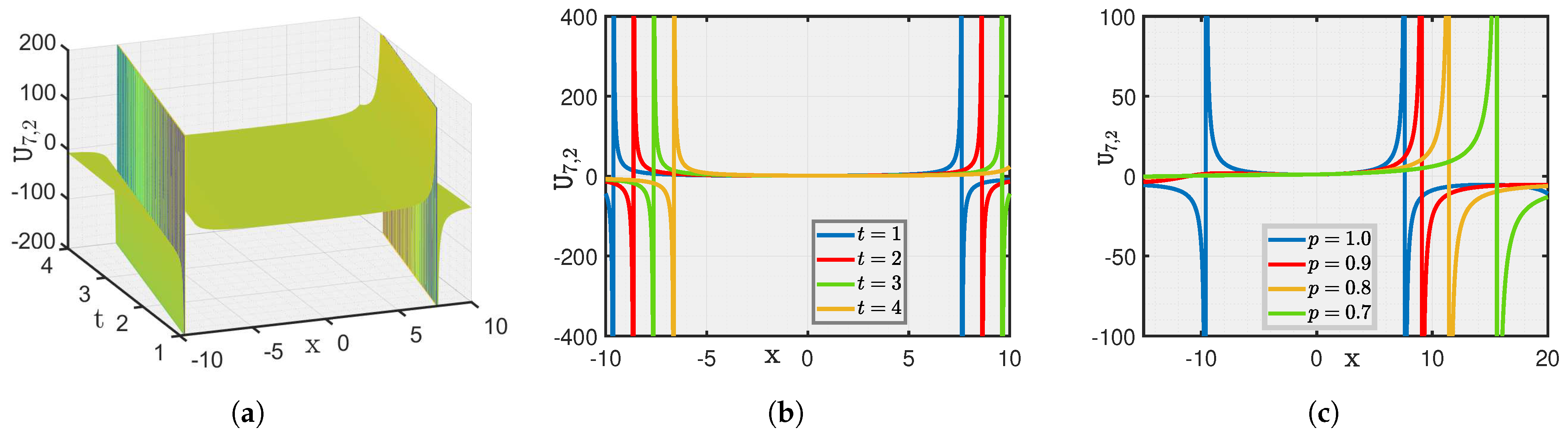
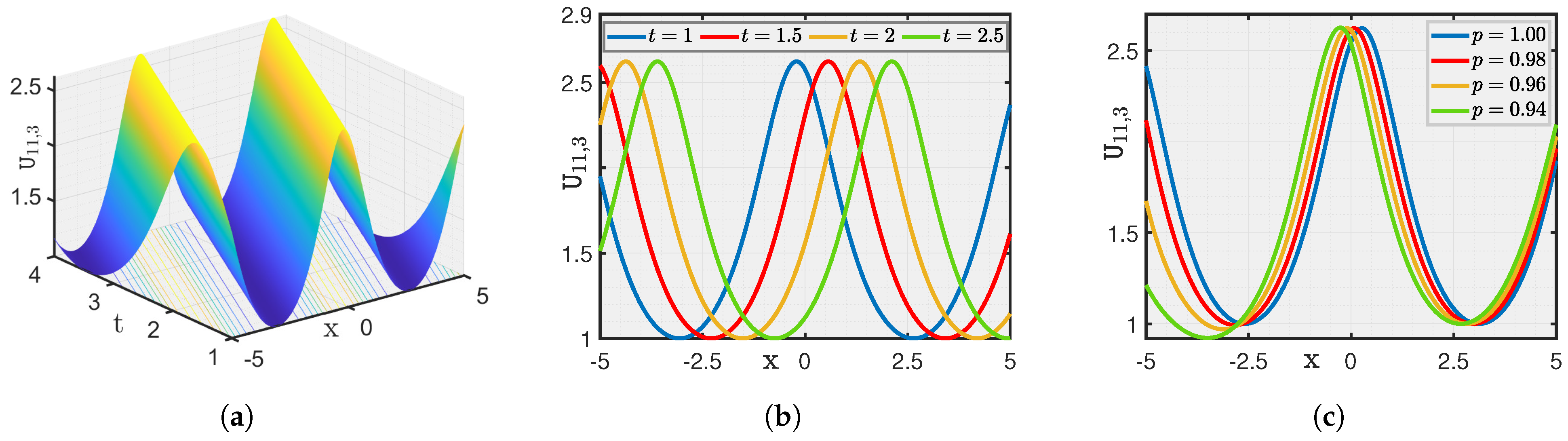
4. Graphical Illustration and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, C.; Zhu, C.X.; Zhang, N.; Sui, S.H.; Zhao, J.B. Free vibration of self-powered nanoribbons subjected to thermal-mechanical-electrical fields based on a nonlocal strain gradient theory. Appl. Math. Model. 2022, 110, 583–602. [Google Scholar] [CrossRef]
- Zhu, C.; Chen, Y.; Zhao, J.; Li, C.; Lei, Z. On Nonlocal Vertical and Horizontal Bending of a Micro-Beam. Math. Probl. Eng. 2022, 2022, 5121377. [Google Scholar] [CrossRef]
- Xu, C.; Farman, M.; Shehzad, A. Analysis and chaotic behavior of a fish farming model with singular and non-singular kernel. Int. J. Biomath. 2023. [Google Scholar] [CrossRef]
- Xu, C.; Liao, M.; Farman, M.; Shehzad, A. Hydrogenolysis of glycerol by heterogeneous ca-talysis: A fractional order kinetic model with analysis. MATCH Commun. Math. Comput. Chem. 2024, 91, 635–664. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Sutradhar, T.; Datta, B.K.; Bera, R.K. Analytical solution of the time fractional Fokker-Planck equation. Int. J. Appl. Mech. Eng. 2014, 19, 435–440. [Google Scholar] [CrossRef]
- Khan, A.; Akram, T.; Khan, A.; Ahmad, S.; Nonlaopon, K. Investigation of time fractional nonlinear KdV-Burgers equation under fractional operators with nonsingular kernels. AIMS Math 2023, 8, 1251–1268. [Google Scholar] [CrossRef]
- Guo, L.; Li, C.; Zhao, J. Existence of Monotone Positive Solutions for Caputo–Hadamard Nonlinear Fractional Differential Equation with Infinite-Point Boundary Value Conditions. Symmetry 2023, 15, 970. [Google Scholar] [CrossRef]
- Nieto, J.J.; Khastan, A.; Ivaz, K. Numerical solution of fuzzy differential equations under generalized differentiability. Nonlinear Anal. Hybrid Syst. 2009, 3, 700–707. [Google Scholar] [CrossRef]
- Collegari, R.; Federson, M.; Frasson, M. Linear FDEs in the frame of general-ized ODEs: Variation-of-constants formula. Czechoslov. Math. J. 2018, 68, 889–920. [Google Scholar] [CrossRef]
- Khan, A.; Ali, A.; Ahmad, S.; Saifullah, S.; Nonlaopon, K.; Akgül, A. Nonlinear Schrö-dinger equation under non-singular fractional operators: A computational study. Results Phys. 2022, 43, 106062. [Google Scholar] [CrossRef]
- Duan, J.S.; Rach, R.; Baleanu, D.; Wazwaz, A.M. A review of the Adomian de-composition method and its applications to fractional differential equations. Commun. Fract. Calc. 2012, 3, 73–99. [Google Scholar]
- He, J.-H. Recent development of the homotopy perturbation method. Topol. Methods Nonlinear Anal. 2008, 31, 205–209. [Google Scholar]
- Abdou, M.A.; Soliman, A.A. New applications of variational iteration method. Phys. D Nonlinear Phenom. 2005, 211, 1–8. [Google Scholar] [CrossRef]
- Podlubny, I.; Chechkin, A.; Skovranek, T.; Chen, Y.; Jara, B.M. Matrix approach to discrete fractional calculus II: Partial fractional differential equations. J. Comput. Phys. 2009, 228, 3137–3153. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Miah, M.M.; Ali, H.S.; Shahen, N.H.M.; Deifalla, A. New applications of the fractional derivative to extract abundant soliton solutions of the fractional order PDEs in mathematics physics. Partial. Differ. Equ. Appl. Math. 2024, 9, 100597. [Google Scholar] [CrossRef]
- Younas, U.; Yao, F.; Nasreen, N.; Khan, A.; Abdeljawad, T. On the dynamics of soliton solutions for the nonlinear fractional dynamical system: Application in ultrasound imaging. Results Phys. 2024, 57, 107349. [Google Scholar] [CrossRef]
- Yasin, S.; Khan, A.; Ahmad, S.; Osman, M.S. New exact solutions of (3+1)-dimensional modified KdV-Zakharov-Kuznetsov equation by Sardar-subequation method. Opt. Quantum Electron. 2024, 56, 90. [Google Scholar] [CrossRef]
- Khan, A.; Khan, A.U.; Ahmad, S. Investigation of fractal fractional nonlinear Korteweg-de-Vries-Schrödinger system with power law kernel. Phys. Scr. 2023, 98, 085202. [Google Scholar] [CrossRef]
- Baber, M.Z.; Ahmed, N.; Xu, C.; Iqbal, M.S.; Sulaiman, T.A. A computational scheme and its comparison with optical soliton solutions for the stochastic Chen–Lee–Liu equation with sensitivity analysis. Mod. Phys. Lett. B 2024, 2450376. [Google Scholar] [CrossRef]
- Li, P.; Shi, S.; Xu, C.; ur Rahman, M. Bifurcations, chaotic behavior, sensitivity analysis and new optical solitons solutions of Sasa-Satsuma equation. Nonlinear Dyn. 2024, 112, 7405–7415. [Google Scholar] [CrossRef]
- Akram, W.; Ullah, A.; Ali, S.; Ahmad, S. Exploration of soliton solution of coupled Drinfel’d–Sokolov–Wilson equation under conformable differential operator. Partial. Differ. Equ. Appl. Math. 2024, 10, 100708. [Google Scholar] [CrossRef]
- Saifullah, S.; Ahmad, S.; Khan, M.A.; ur Rahman, M. Multiple solitons with fission and multi waves interaction solutions of a (3+1)-dimensional combined pKP-BKP integrable equation. Phys. Scr. 2024, 99, 065242. [Google Scholar] [CrossRef]
- Zhu, C.; Al-Dossari, M.; Rezapour, S.; Alsallami, S.A.M.; Gunay, B. Bifurcations, chaotic be-havior, and optical solutions for the complex Ginzburg–Landau equation. Results Phys. 2024, 59, 107601. [Google Scholar] [CrossRef]
- Zhu, C.; Al-Dossari, M.; Rezapour, S.; Gunay, B. On the exact soliton solutions and different wave structures to the (2+1) dimensional Chaffee–Infante equation. Results Phys. 2024, 57, 107431. [Google Scholar] [CrossRef]
- Zhu, C.; Al-Dossari, M.; Rezapour, S.; Shateyi, S.; Gunay, B. Analytical optical solutions to the nonlinear Zakharov system via logarithmic transformation. Results Phys. 2024, 56, 107298. [Google Scholar] [CrossRef]
- Kai, Y.; Ji, J.; Yin, Z. Study of the generalization of regularized long-wave equation. Nonlinear Dyn. 2022, 107, 2745–2752. [Google Scholar] [CrossRef]
- Kai, Y.; Yin, Z. Linear structure and soliton molecules of Sharma-Tasso-Olver-Burgers equation. Phys. Lett. A 2022, 452, 128430. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S. Improved fractional sub-equation method for (3+1)-dimensional generalized fractional KdV–Zakharov–Kuznetsov equations. Comput. Math. Appl. 2015, 70, 158–166. [Google Scholar] [CrossRef]
- Guner, O. New exact solutions to the space–time fractional nonlinear wave equation obtained by the ansatz and functional variable methods. Opt. Quantum Electron. 2018, 50, 38. [Google Scholar] [CrossRef]
- Christiano, L.J. Solving dynamic equilibrium models by a method of unde-termined coefficients. Comput. Econ. 2002, 20, 21–55. [Google Scholar] [CrossRef]
- Park, C.; Nuruddeen, R.I.; Ali, K.K.; Muhammad, L.; Osman, M.S.; Baleanu, D. Novel hyperbolic and exponential ansatz methods to the fractional fifth-order Korteweg–de Vries equations. Adv. Differ. Equ. 2020, 2020, 627. [Google Scholar] [CrossRef]
- Liu, W.; Chen, K. The functional variable method for finding exact solutions of some nonlinear time-fractional differential equations. Pramana 2013, 81, 377–384. [Google Scholar] [CrossRef]
- Nisar, K.S.; Ilhan, O.A.; Abdulazeez, S.T.; Manafian, J.; Mohammed, S.A.; Osman, M.S. Novel multiple soliton solutions for some nonlinear PDEs via multiple Exp-function method. Results Phys. 2021, 21, 103769. [Google Scholar] [CrossRef]
- Jumarie, G. Modified Riemann–Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput. Math. Appl. 2006, 51, 1367–1376. [Google Scholar] [CrossRef]
- Jumarie, G. Table of some basic fractional calculus formulae derived from a mod-ified Riemann–Liouvillie derivative for nondifferentiable functions. Appl. Math. Lett. 2009, 22, 378–385. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamza, A.E.; Osman, O.; Sarwar, M.U.; Aldwoah, K.; Saber, H.; Hleili, M. Exploring Solitons Solutions of a (3+1)-Dimensional Fractional mKdV-ZK Equation. Fractal Fract. 2024, 8, 498. https://doi.org/10.3390/fractalfract8090498
Hamza AE, Osman O, Sarwar MU, Aldwoah K, Saber H, Hleili M. Exploring Solitons Solutions of a (3+1)-Dimensional Fractional mKdV-ZK Equation. Fractal and Fractional. 2024; 8(9):498. https://doi.org/10.3390/fractalfract8090498
Chicago/Turabian StyleHamza, Amjad E., Osman Osman, Muhammad Umair Sarwar, Khaled Aldwoah, Hicham Saber, and Manel Hleili. 2024. "Exploring Solitons Solutions of a (3+1)-Dimensional Fractional mKdV-ZK Equation" Fractal and Fractional 8, no. 9: 498. https://doi.org/10.3390/fractalfract8090498
APA StyleHamza, A. E., Osman, O., Sarwar, M. U., Aldwoah, K., Saber, H., & Hleili, M. (2024). Exploring Solitons Solutions of a (3+1)-Dimensional Fractional mKdV-ZK Equation. Fractal and Fractional, 8(9), 498. https://doi.org/10.3390/fractalfract8090498







