Feedback Control Design Strategy for Stabilization of Delayed Descriptor Fractional Neutral Systems with Order 0 < ϱ < 1 in the Presence of Time-Varying Parametric Uncertainty
Abstract
1. Introduction
- •
- The L-K functional technique is adopted to study the asymptotical stability of FDSs with neutral-type delay subject to time-varying delays and parametric uncertainties.
- •
- Static state- and output-feedback controllers are designed to ensure regularity and impulse-free properties together, and delay-dependent and order-dependent conditions are achieved in the form of LMIs for the existence of such controllers.
2. Theoretical Background
3. Formulation of the Problem
General Assumptions and Control Goals
- A1: The uncertainty terms satisfywhere the real constant matrices and , are known and have compatible sizes, and the time-varying matrix is real, unknown and satisfies .
- A2: The delay is continuous with bounded derivative satisfyingin which and are constants.
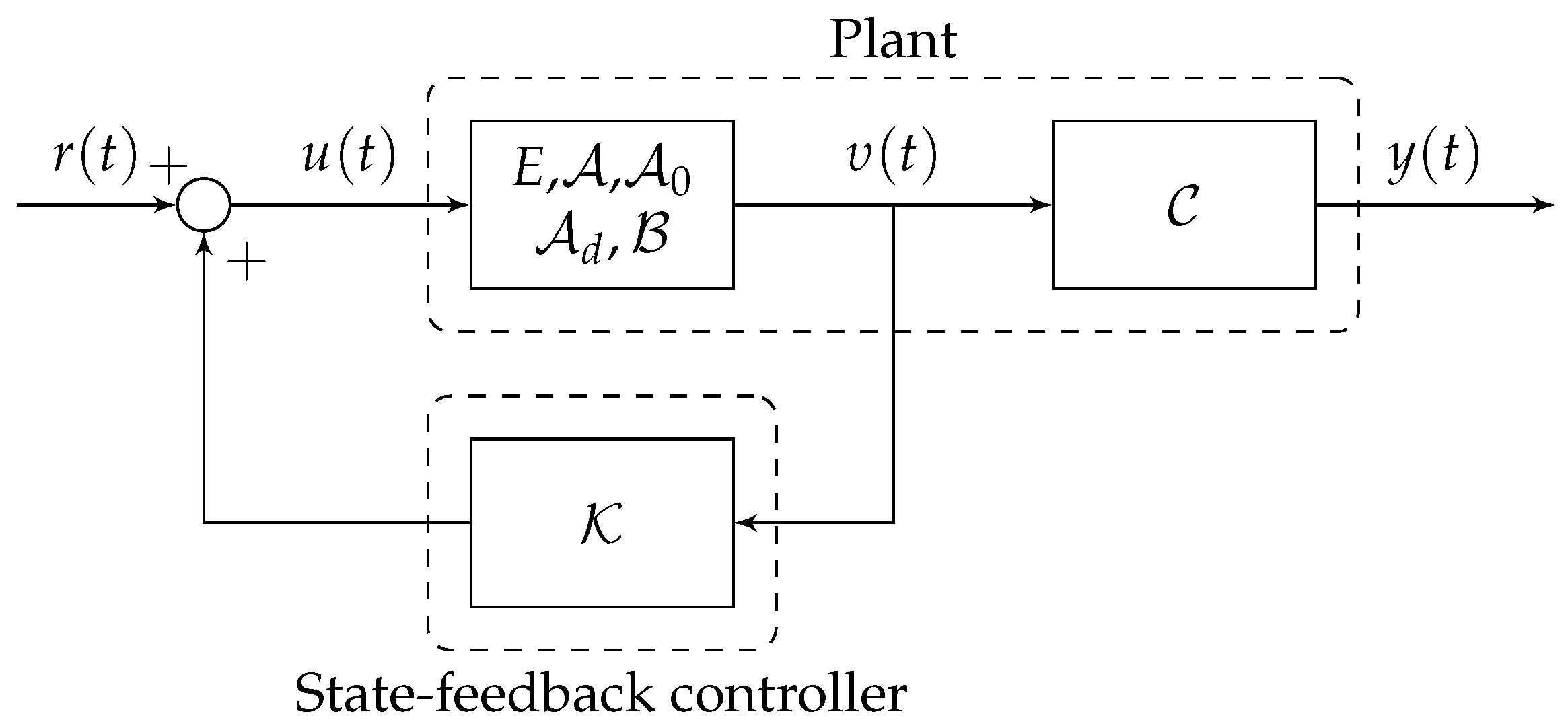
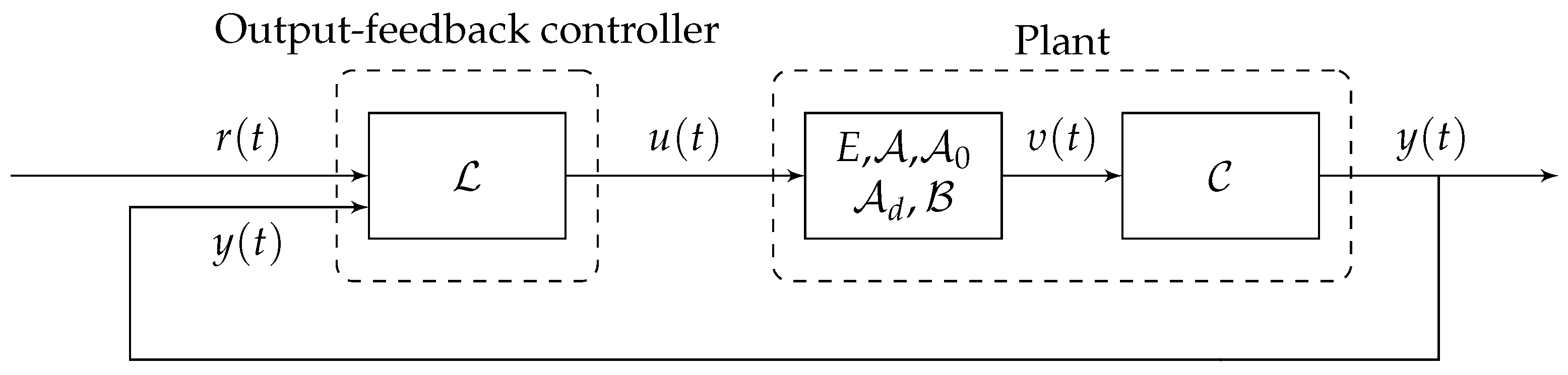
- A3: The static state- and output-feedback techniques are adopted for control, which are given bywhere and denote the state and output controller gains, respectively, which are computed based on LMI conditions.
4. Stability Analysis
4.1. Nominal Stability
4.2. Robust Stability
5. Control Design
5.1. Nominal Stabilization
5.2. Robust Stabilization
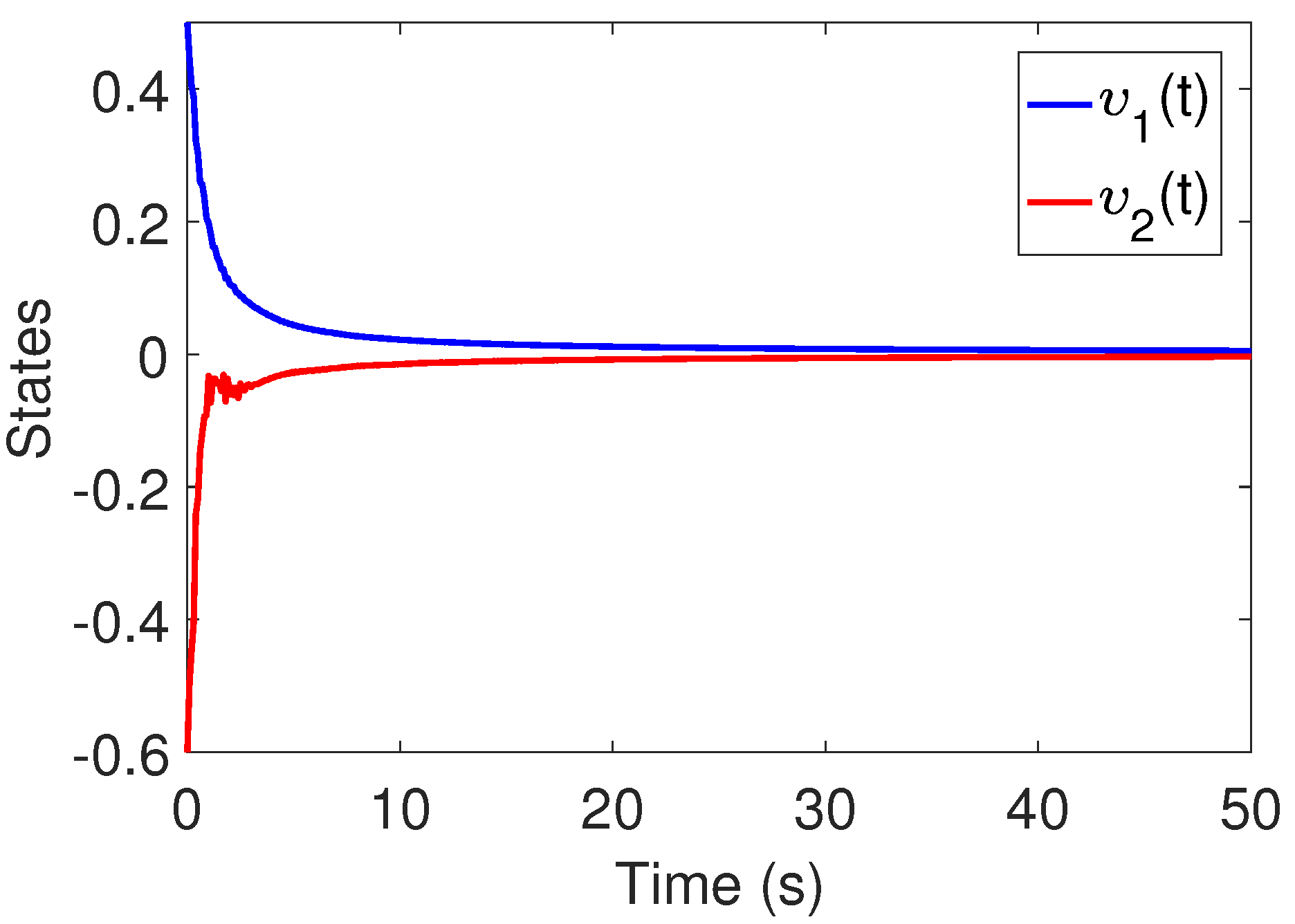
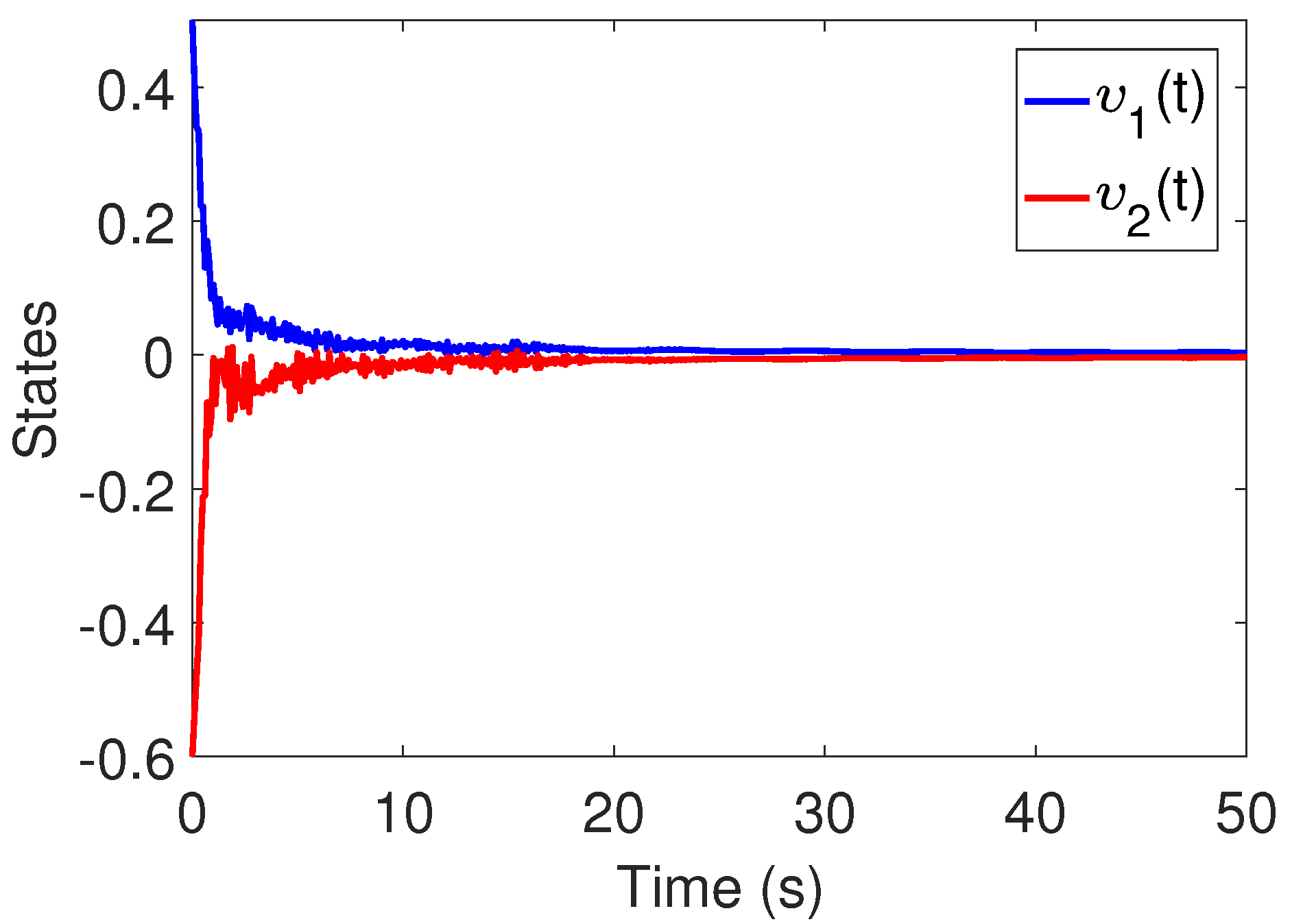
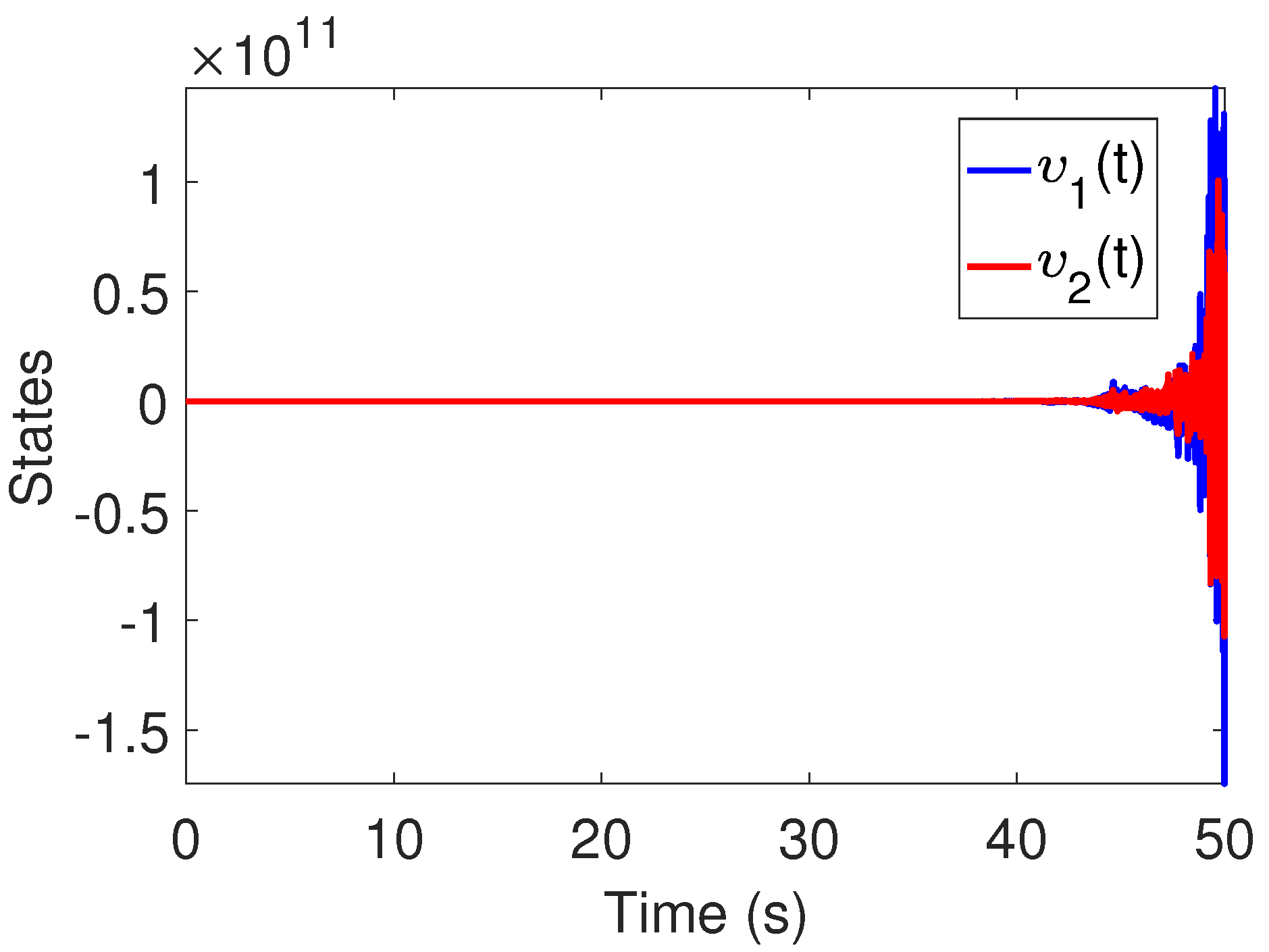
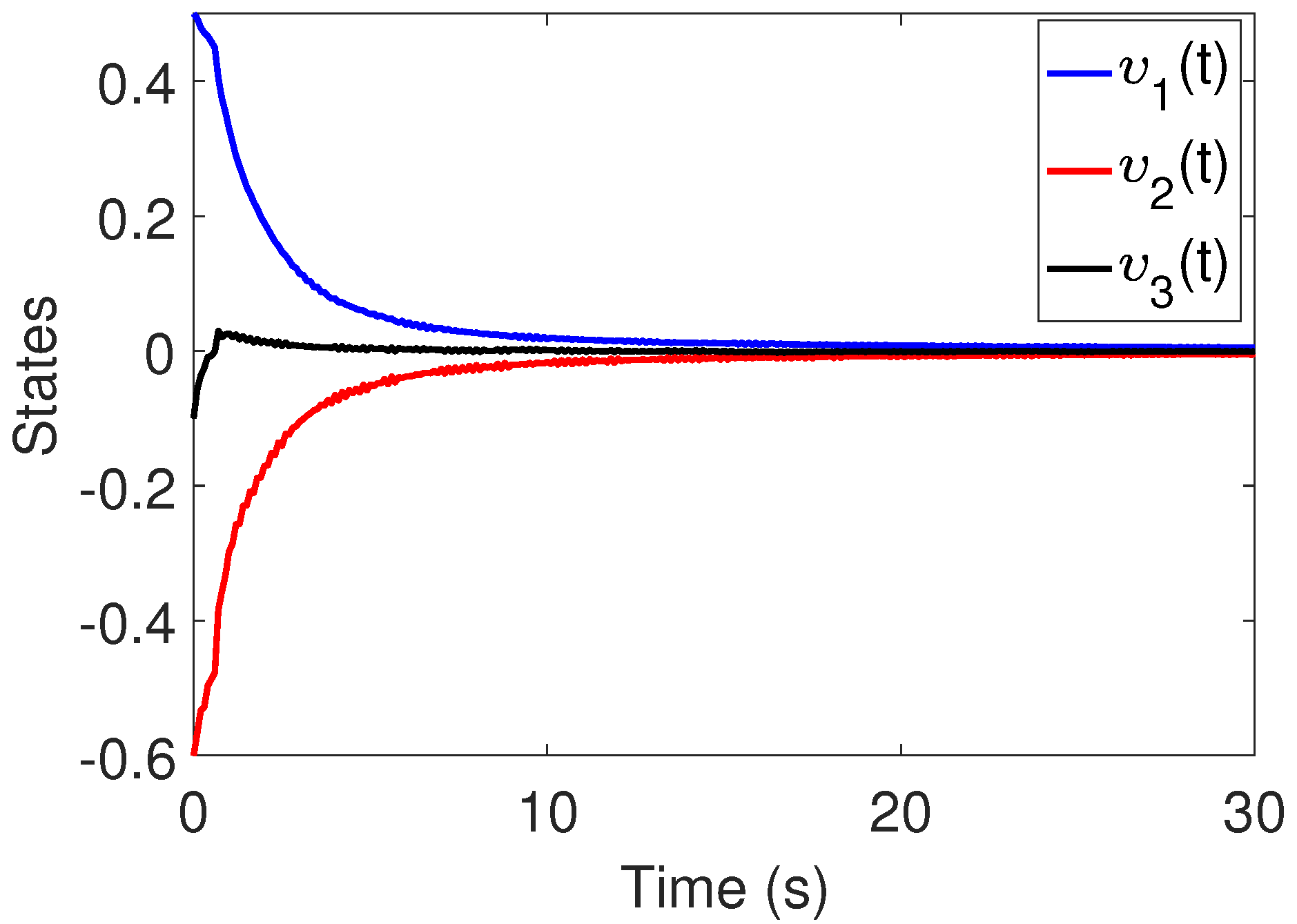
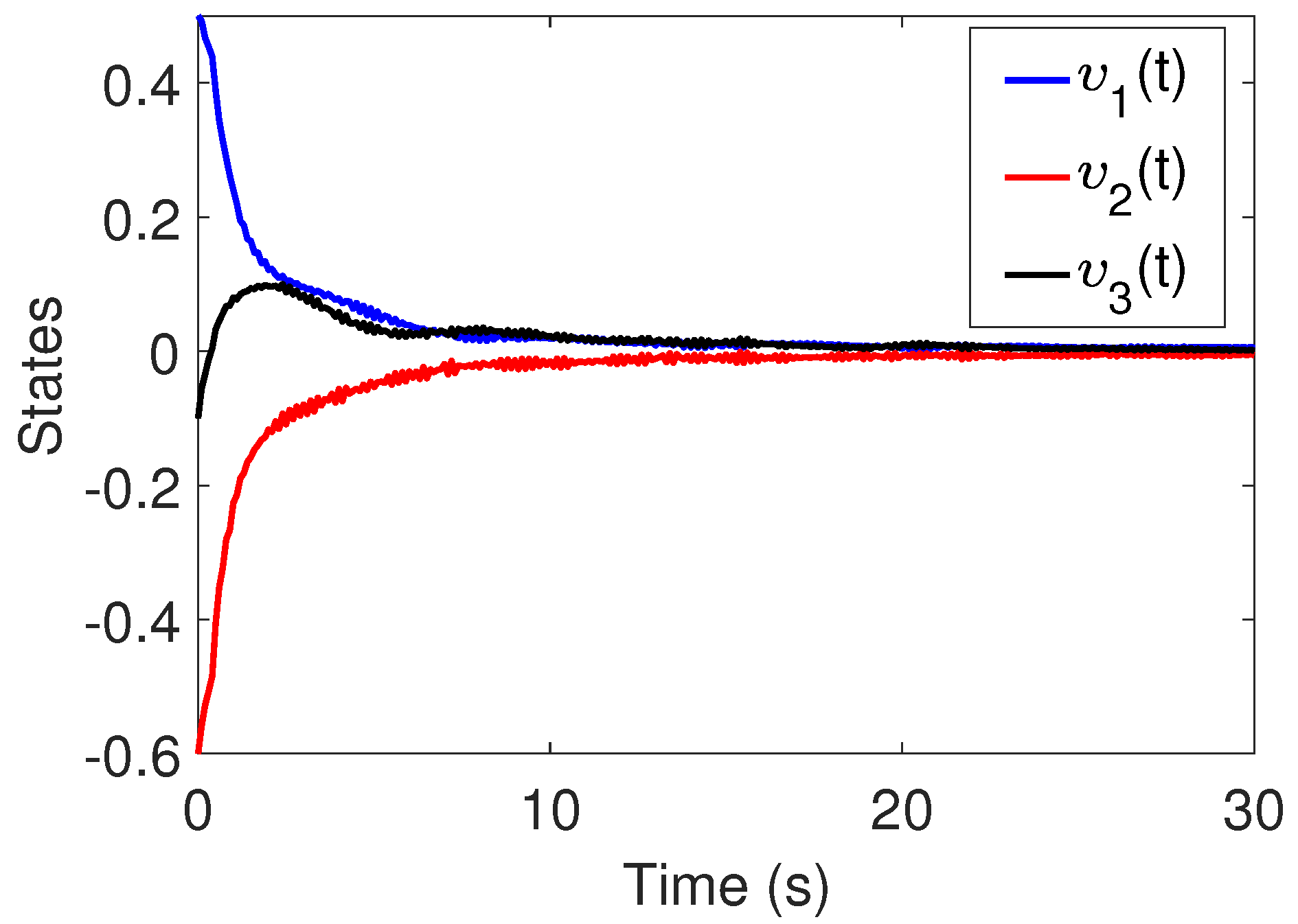
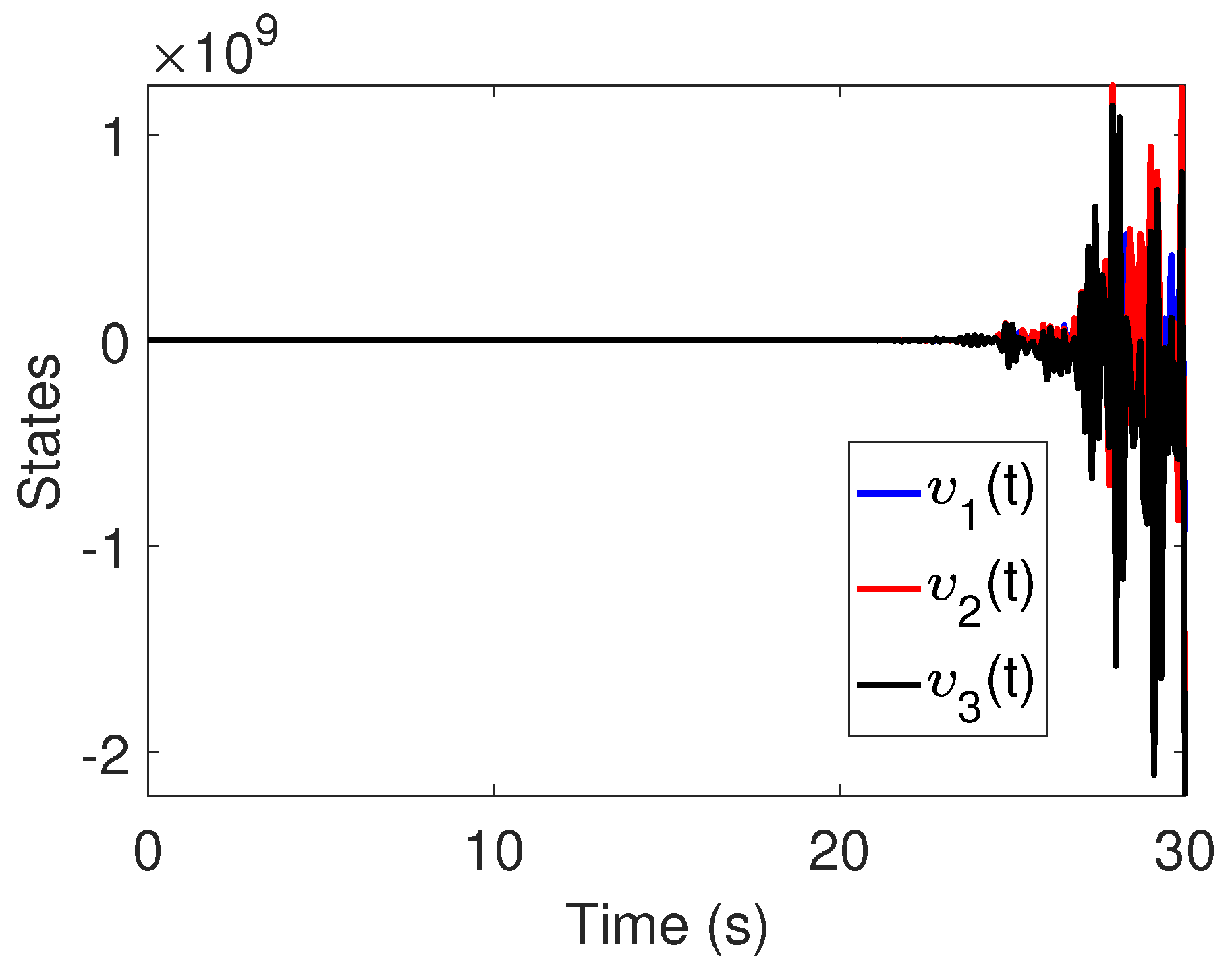
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dai, L. Singular Control Systems; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Xu, S.; Lam, J. Robust Control and Filtering of Singular Systems; Springer: Berlin/Heidelberg, Germany, 2006; Volume 332. [Google Scholar]
- Di, Y.; Zhang, J.X.; Zhang, X. Alternate admissibility LMI criteria for descriptor fractional order systems with 0 < α < 2. Fractal Fract. 2023, 7, 577. [Google Scholar]
- Yang, H.; Si, X.; Ivanov, I.G. Constrained State Regulation Problem of Descriptor Fractional-Order Linear Continuous-Time Systems. Fractal Fract. 2024, 8, 255. [Google Scholar] [CrossRef]
- Lewis, F.L. A survey of linear singular systems. Circuits Syst. Signal Process. 1986, 5, 3–36. [Google Scholar] [CrossRef]
- Feng, Y.; Yagoubi, M. Robust Control of Linear Descriptor Systems; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kaczorek, T.; Borawski, K. Descriptor Systems of Integer and Fractional Orders; Springer: Berlin/Heidelberg, Germany, 2021; Volume 367. [Google Scholar]
- Zhuang, G.; Ma, Q.; Zhang, B.; Xu, S.; Xia, J. Admissibility and stabilization of stochastic singular Markovian jump systems with time delays. Syst. Control. Lett. 2018, 114, 1–10. [Google Scholar] [CrossRef]
- Wang, H.; Xue, A.; Lu, R. Absolute stability criteria for a class of nonlinear singular systems with time delay. Nonlinear Anal. Theory Methods Appl. 2009, 70, 621–630. [Google Scholar] [CrossRef]
- Long, S.; Zhong, S. Improved results for stochastic stabilization of a class of discrete-time singular Markovian jump systems with time-varying delay. Nonlinear Anal. Hybrid Syst. 2017, 23, 11–26. [Google Scholar] [CrossRef]
- Liu, G. New results on stability analysis of singular time-delay systems. Int. J. Syst. Sci. 2017, 48, 1395–1403. [Google Scholar] [CrossRef]
- Aghayan, Z.S.; Alfi, A.; Machado, J.T. Delay-dependent robust stability analysis of uncertain fractional-order neutral systems with distributed delays and nonlinear perturbations subject to input saturation. Int. J. Nonlinear Sci. Numer. Simul. 2023, 24, 329–347. [Google Scholar] [CrossRef]
- Salamon, D. Control and Observation of Neutral Systems; Number 91; Pitman Advanced Publishing Program: Boston, MA, USA, 1984. [Google Scholar]
- Han, Q.L. Stability analysis for a partial element equivalent circuit (PEEC) model of neutral type. Int. J. Circuit Theory Appl. 2005, 33, 321–332. [Google Scholar] [CrossRef]
- Cui, K.; Lu, J.; Li, C.; He, Z.; Chu, Y.M. Almost sure synchronization criteria of neutral-type neural networks with Lévy noise and sampled-data loss via event-triggered control. Neurocomputing 2019, 325, 113–120. [Google Scholar] [CrossRef]
- Kuang, Y. Delay Differential Equations: With Applications in Population Dynamics; Academic Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Chen, W.; Zhuang, G.; Xu, S.; Liu, G.; Li, Y.; Zhang, Z. New results on stabilization for neutral type descriptor hybrid systems with time-varying delays. Nonlinear Anal. Hybrid Syst. 2022, 45, 101172. [Google Scholar] [CrossRef]
- Chen, W.b.; Gao, F. New results on stability analysis for a kind of neutral singular systems with mixed delays. Eur. J. Control 2020, 53, 59–67. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Q.; Xiao, D.; Bai, F. Robust stability analysis and stabilisation of uncertain neutral singular systems. Int. J. Syst. Sci. 2016, 47, 3762–3771. [Google Scholar] [CrossRef]
- Guo, Y.; Li, T. Fractional-order modeling and optimal control of a new online game addiction model based on real data. Commun. Nonlinear Sci. Numer. Simul. 2023, 121, 107221. [Google Scholar] [CrossRef]
- Chen, Y.; Lv, Z. A fractional optimal control model for a simple cash balance problem. Commun. Nonlinear Sci. Numer. Simul. 2023, 120, 107194. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. The 21st century systems: An updated vision of continuous-time fractional models. IEEE Circuits Syst. Mag. 2022, 22, 36–56. [Google Scholar] [CrossRef]
- Abdoon, M.A.; Saadeh, R.; Berir, M.; Guma, F.E.; ali, M. Analysis, modeling and simulation of a fractional-order influenza model. Alex. Eng. J. 2023, 74, 231–240. [Google Scholar] [CrossRef]
- Yunus, A.O.; Olayiwola, M.O.; Omoloye, M.A.; Oladapo, A.O. A fractional order model of lassa disease using the Laplace-adomian decomposition method. Healthc. Anal. 2023, 3, 100167. [Google Scholar] [CrossRef]
- Mok, R.; Ahmad, M.A. Smoothed functional algorithm with norm-limited update vector for identification of continuous-time fractional-order Hammerstein models. IETE J. Res. 2024, 70, 1814–1832. [Google Scholar] [CrossRef]
- Baleanu, D.; Sadat Sajjadi, S.; Jajarmi, A.; Asad, J.H. New features of the fractional Euler-Lagrange equations for a physical system within non-singular derivative operator. Eur. Phys. J. Plus 2019, 134, 1–10. [Google Scholar] [CrossRef]
- Valério, D.; Ortigueira, M.D.; Lopes, A.M. How many fractional derivatives are there? Mathematics 2022, 10, 737. [Google Scholar] [CrossRef]
- Yakoub, Z.; Aoun, M.; Amairi, M.; Chetoui, M. Identification of continuous-time fractional models from noisy input and output signals. In Fractional Order Systems—Control Theory and Applications: Fundamentals and Applications; Springer: Cham, Switzerland, 2022; pp. 181–216. [Google Scholar]
- Ortigueira, M.D.; Ionescu, C.M.; Machado, J.T.; Trujillo, J.J. Fractional signal processing and applications. Signal Process. 2015, 107, 197. [Google Scholar] [CrossRef]
- Ostalczyk, P. Discrete Fractional Calculus: Applications in Control and Image Processing; World Scientific: Singapore, 2015; Volume 4. [Google Scholar]
- Safaei, M.; Tavakoli, S. Smith predictor based fractional-order control design for time-delay integer-order systems. Int. J. Dyn. Control 2018, 6, 179–187. [Google Scholar] [CrossRef]
- Modiri, A.; Mobayen, S. Adaptive terminal sliding mode control scheme for synchronization of fractional-order uncertain chaotic systems. ISA Trans. 2020, 105, 33–50. [Google Scholar] [CrossRef]
- Baishya, C.; Premakumari, R.; Samei, M.E.; Naik, M.K. Chaos control of fractional order nonlinear Bloch equation by utilizing sliding mode controller. Chaos Solitons Fractals 2023, 174, 113773. [Google Scholar] [CrossRef]
- Caponetto, R. Fractional Order Systems: Modeling and Control Applications; World Scientific: Singapore, 2010; Volume 72. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Wei, Y.; Zhao, L.; Wei, Y.; Cao, J. Lyapunov theorem for stability analysis of nonlinear nabla fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2023, 126, 107443. [Google Scholar] [CrossRef]
- Čermák, J.; Kisela, T. Stabilization and destabilization of fractional oscillators via a delayed feedback control. Commun. Nonlinear Sci. Numer. Simul. 2023, 117, 106960. [Google Scholar] [CrossRef]
- Jia, J.; Huang, X.; Li, Y.; Cao, J.; Alsaedi, A. Global stabilization of fractional-order memristor-based neural networks with time delay. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 997–1009. [Google Scholar] [CrossRef] [PubMed]
- Hei, X.; Wu, R. Finite-time stability of impulsive fractional-order systems with time-delay. Appl. Math. Model. 2016, 40, 4285–4290. [Google Scholar] [CrossRef]
- Yu, R.; Wang, D. Structural properties and poles assignability of LTI singular systems under output feedback. Automatica 2003, 39, 685–692. [Google Scholar] [CrossRef]
- Chen, W.H.; Zheng, W.X.; Lu, X. Impulsive stabilization of a class of singular systems with time-delays. Automatica 2017, 83, 28–36. [Google Scholar] [CrossRef]
- Sadati, M.; Hosseinzadeh, M.; Shafiee, M. Modelling and analysis of quadruped walking robot using singular system theory. In Proceedings of the 2013 21st Iranian Conference on Electrical Engineering (ICEE), Mashhad, Iran, 14–16 May 2013; pp. 1–6. [Google Scholar]
- Luenberger, D.G.; Arbel, A. Singular dynamic Leontief systems. Econom. J. Econom. Soc. 1977, 45, 991–995. [Google Scholar] [CrossRef]
- Stott, B. Power system dynamic response calculations. Proc. IEEE 1979, 67, 219–241. [Google Scholar] [CrossRef]
- Sell, G.R. Stability theory and Lyapunov’s second method. Arch. Ration. Mech. Anal. 1963, 14, 108–126. [Google Scholar] [CrossRef]
- Zhang, H.; Ye, R.; Liu, S.; Cao, J.; Alsaedi, A.; Li, X. LMI-based approach to stability analysis for fractional-order neural networks with discrete and distributed delays. Int. J. Syst. Sci. 2018, 49, 537–545. [Google Scholar] [CrossRef]
- Chaibi, N.; Tissir, E.H. Delay dependent robust stability of singular systems with time-varying delay. Int. J. Control. Autom. Syst. 2012, 10, 632–638. [Google Scholar] [CrossRef]
- Long, S.; Wu, Y.; Zhong, S.; Zhang, D. Stability analysis for a class of neutral type singular systems with time-varying delay. Appl. Math. Comput. 2018, 339, 113–131. [Google Scholar] [CrossRef]
- Li, D.; Wei, L.; Song, T.; Jin, Q. Study on asymptotic stability of fractional singular systems with time delay. Int. J. Control Autom. Syst. 2020, 18, 1002–1011. [Google Scholar] [CrossRef]
- Liu, X.; Wang, P.; Anderson, D.R. On stability and feedback control of discrete fractional order singular systems with multiple time-varying delays. Chaos Solitons Fractals 2022, 155, 111740. [Google Scholar] [CrossRef]
- Mathiyalagan, K.; Balachandran, K. Finite-time stability of fractional-order stochastic singular systems with time delay and white noise. Complexity 2016, 21, 370–379. [Google Scholar] [CrossRef]
- Qiu, H.; Wang, H.; Pan, Y.; Cao, J.; Liu, H. Stability and L∞-Gain of Positive Fractional-Order Singular Systems with Time-Varying Delays. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 3534–3538. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Zhang, F. The Schur Complement and Its Applications; Springer Science & Business Media: Berlin, Germany, 2006; Volume 4. [Google Scholar]
- Liu, S.; Jiang, W.; Li, X.; Zhou, X.F. Lyapunov stability analysis of fractional nonlinear systems. Appl. Math. Lett. 2016, 51, 13–19. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, M.; Jiang, P. Robust H∞ dynamic output feedback control of linear time-varying periodic fractional order singular systems. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 3066–3071. [Google Scholar]
- Aghayan, Z.S.; Alfi, A.; Machado, J.T. Robust stability of uncertain fractional order systems of neutral type with distributed delays and control input saturation. ISA Trans. 2021, 111, 144–155. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chen, Y. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0 < α <1 case. ISA Trans. 2018, 82, 42–50. [Google Scholar] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aghayan, Z.S.; Alfi, A.; Pahnehkolaei, S.M.A.; Lopes, A.M. Feedback Control Design Strategy for Stabilization of Delayed Descriptor Fractional Neutral Systems with Order 0 < ϱ < 1 in the Presence of Time-Varying Parametric Uncertainty. Fractal Fract. 2024, 8, 481. https://doi.org/10.3390/fractalfract8080481
Aghayan ZS, Alfi A, Pahnehkolaei SMA, Lopes AM. Feedback Control Design Strategy for Stabilization of Delayed Descriptor Fractional Neutral Systems with Order 0 < ϱ < 1 in the Presence of Time-Varying Parametric Uncertainty. Fractal and Fractional. 2024; 8(8):481. https://doi.org/10.3390/fractalfract8080481
Chicago/Turabian StyleAghayan, Zahra Sadat, Alireza Alfi, Seyed Mehdi Abedi Pahnehkolaei, and António M. Lopes. 2024. "Feedback Control Design Strategy for Stabilization of Delayed Descriptor Fractional Neutral Systems with Order 0 < ϱ < 1 in the Presence of Time-Varying Parametric Uncertainty" Fractal and Fractional 8, no. 8: 481. https://doi.org/10.3390/fractalfract8080481
APA StyleAghayan, Z. S., Alfi, A., Pahnehkolaei, S. M. A., & Lopes, A. M. (2024). Feedback Control Design Strategy for Stabilization of Delayed Descriptor Fractional Neutral Systems with Order 0 < ϱ < 1 in the Presence of Time-Varying Parametric Uncertainty. Fractal and Fractional, 8(8), 481. https://doi.org/10.3390/fractalfract8080481









