Advanced Observation-Based Bipartite Containment Control of Fractional-Order Multi-Agent Systems Considering Hostile Environments, Nonlinear Delayed Dynamics, and Disturbance Compensation
Abstract
1. Introduction
- As compared to [29], we use a fractional-order multi-agent system instead of an integer-order derivative; our work contributes to the field by providing a more general and flexible framework for modeling and controlling dynamic behaviors in complex networks.
- By incorporating disturbances into the controller, our work enhances the robustness and practical applicability of the control strategy for fractional-order multi-agent systems, addressing real-world uncertainties.
- By incorporating a nonlinear delayed function in the dynamics, our work provides a more accurate and comprehensive framework for modeling and controlling fractional-order multi-agent systems, capturing complex temporal interactions and delays that have not been addressed in previous studies [29].
- 1.
- Section 1 is the introduction of the paper.
- 2.
- Section 2 presents the foundational knowledge that is useful for our main results.
- 3.
- Observation-based analyses of bipartite containment control for fixed and switching signed digraphs are discussed in Section 3.2 and Section 4.
- 4.
- Numerical examples are presented in Section 5.
- 5.
- The paper is summarized in Section 6.
2. Foundational Knowledge
2.1. Graph Theory
2.2. Basic Lemmas and Fractional Operators
3. Observation-Based Bipartite Containment Control Analysis
3.1. Model Building
3.2. Observation-Based Analysis of Bipartite Multi-Agent System for Fixed Signed Digraph
- , where:
- -
- -
- , where:
- -
- -
4. Observation-Based Analysis of Bipartite Containment Control for Switching Signed Digraph
- , where:
- -
- -
- , where:
- -
- -
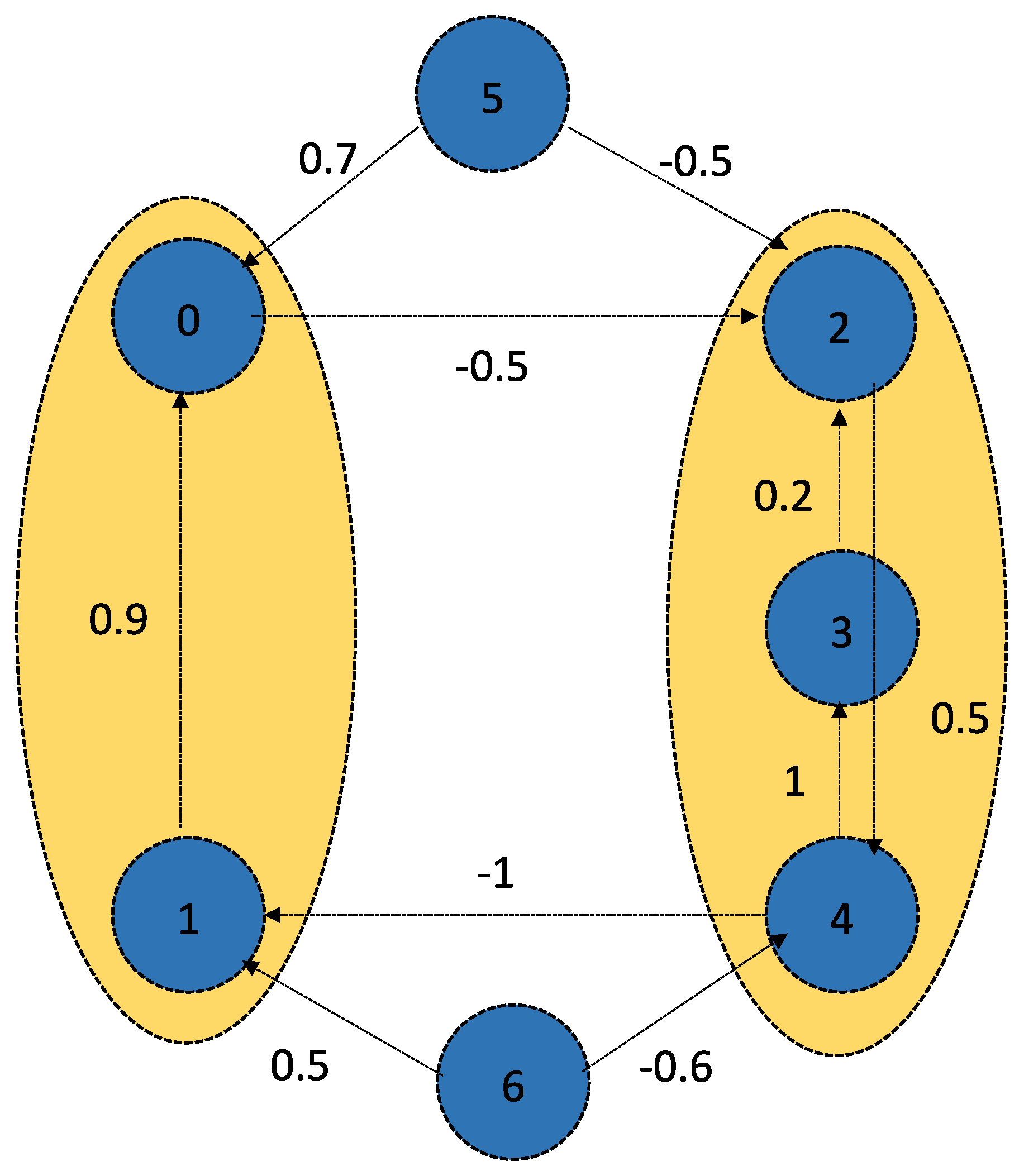
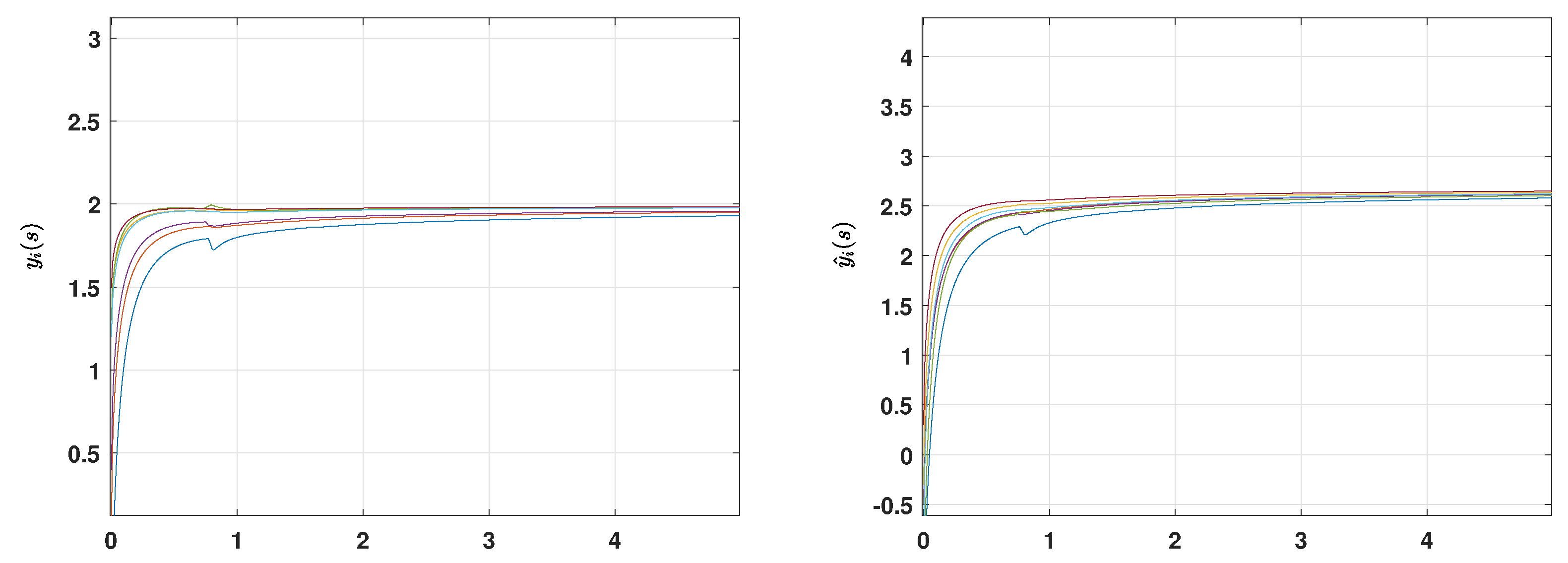
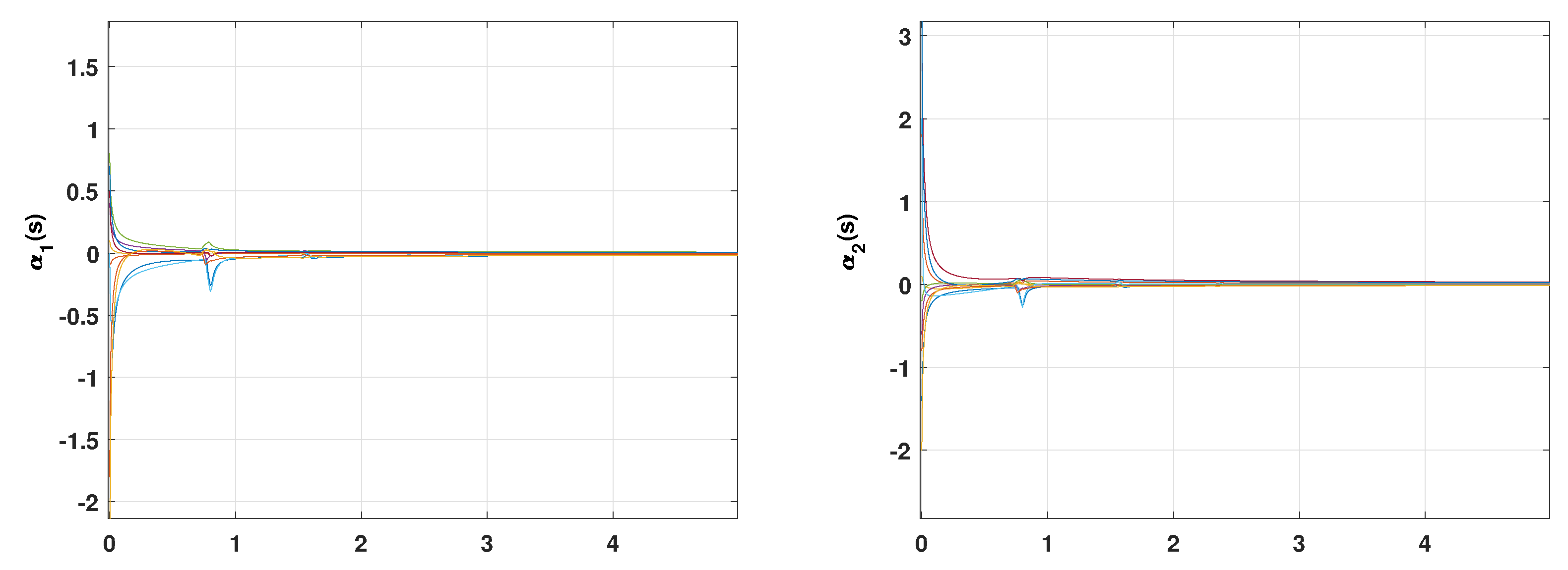
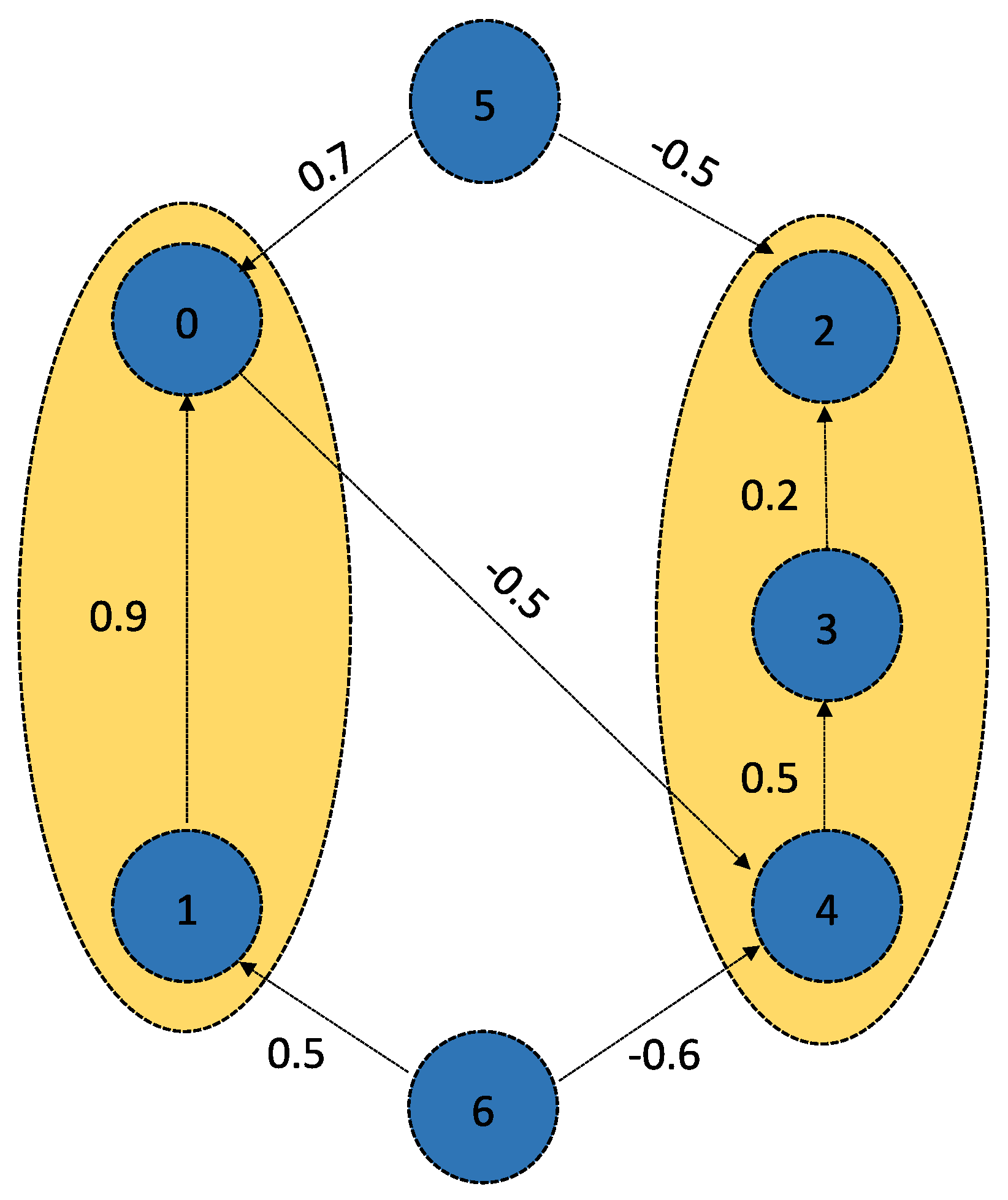
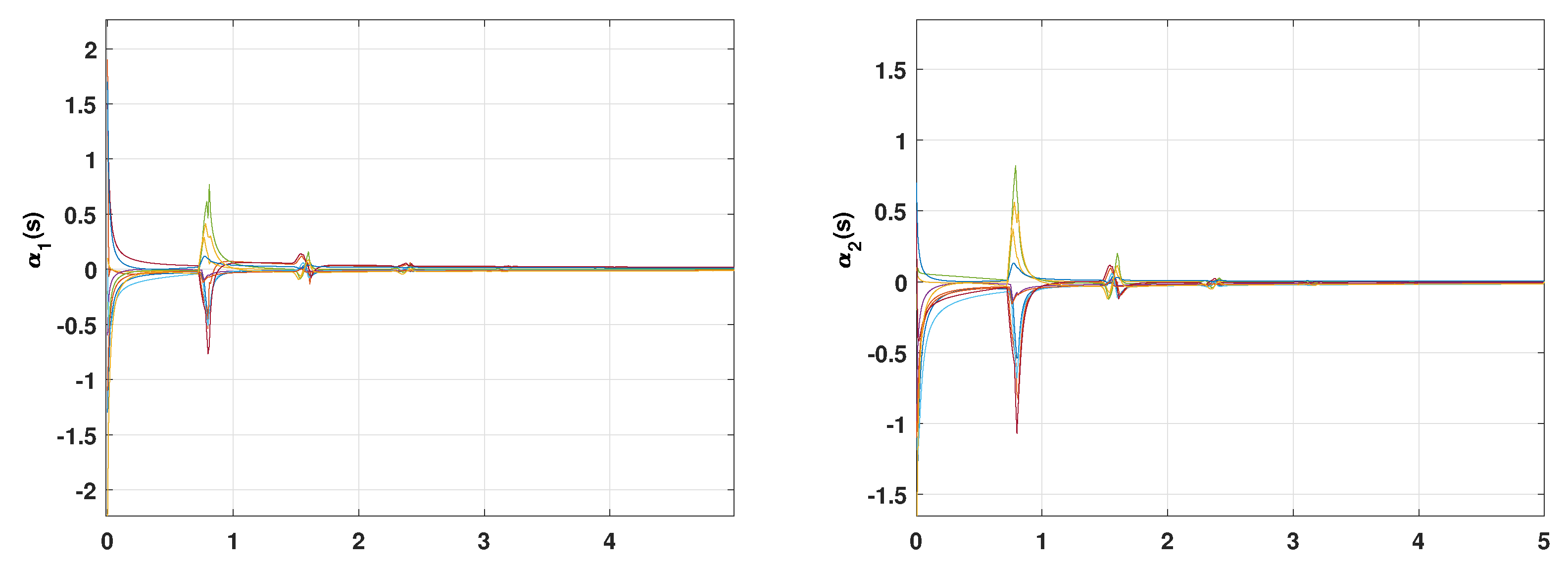
5. Numerical Illustrations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dai, J.; Guo, G. Event-triggered leader-following consensus for multi-agent systems with semi-Markov switching topologies. Inf. Sci. 2018, 459, 290–301. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, S. Exponential Consensus of Multi-Agent Systems under Event-Triggered Impulsive Control with Actuation Delays. Entropy 2023, 25, 877. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.; Wang, F.; Chen, Z. Rotating Consensus for Leader-Follower Multi-Agent Systems with a Smart Leader. In Proceedings of the 2023 42nd Chinese Control Conference (CCC), Tianjin, China, 24–26 July 2023; pp. 5719–5724. [Google Scholar]
- Ali, M.S.; Agalya, R.; Orman, Z.; Arik, S. Leader-following consensus of non-linear multi-agent systems with interval time-varying delay via impulsive control. Neural Process. Lett. 2021, 53, 69–83. [Google Scholar] [CrossRef]
- Ali, M.S.; Agalya, R.; Shekher, V.; Joo, Y.H. Non–fragile sampled data control for stabilization of non-linear multi-agent system with additive time varying delays, Markovian jump and uncertain parameters. Nonlinear Anal. Hybrid Syst. 2020, 36, 100830. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, X.; Yu, J.; Shi, P. Output feedback-based neural adaptive finite-time containment control of non-strict feedback nonlinear multi-agent systems. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 69, 847–858. [Google Scholar] [CrossRef]
- Mohammed, K.S.; Pata, U.K. Linking the utilization of mineral resources and climate change: A novel approach with frequency domain analysis. Geosci. Front. 2024, 15, 101683. [Google Scholar] [CrossRef]
- Jiang, Y.; Fan, J.; Gao, W.; Chai, T.; Lewis, F.L. Cooperative adaptive optimal output regulation of nonlinear discrete-time multi-agent systems. Automatica 2020, 121, 109149. [Google Scholar] [CrossRef]
- Khan, A.; Niazi, A.U.K.; Rehman, S.; Ahmed, S. Hostile-based bipartite containment control of nonlinear fractional multi-agent systems with input delays: A signed graph approach under disturbance and switching networks. AIMS Math. 2024, 9, 12678–12699. [Google Scholar] [CrossRef]
- Yang, R.; Liu, S.; Li, X.; Xiao, J. Bipartite containment control of fractional multi-agent systems with input delay on switching signed directed networks. ISA Trans. 2023, 135, 130–137. [Google Scholar] [CrossRef]
- Yin, M.; Liu, L.; Cheng, L.; Li, Z.; Tu, Y. A novel group multi-criteria sorting approach integrating social network analysis for ability assessment of health rumor-refutation accounts. Expert Syst. Appl. 2024, 238, 121894. [Google Scholar] [CrossRef]
- Madridano, Á.; Al-Kaff, A.; Martín, D.; De La Escalera, A. Trajectory planning for multi-robot systems: Methods and applications. Expert Syst. Appl. 2021, 173, 114660. [Google Scholar] [CrossRef]
- Meng, X.; Gao, H. High-order bipartite containment control in multi-agent systems over time-varying cooperation-competition networks. Neurocomputing 2019, 359, 509–516. [Google Scholar] [CrossRef]
- Liu, Z.; Zhan, X.; Han, T.; Yan, H. Distributed adaptive finite-time bipartite containment control of linear multi-agent systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4354–4358. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Hu, B.; Guan, Z.H.; Zhang, D.X.; Li, T. Observer-based bipartite containment control for singular multi-agent systems over signed digraphs. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 68, 444–457. [Google Scholar] [CrossRef]
- Ahsan, M.; Ma, Q. Bipartite containment control of multi-agent systems. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 895–900. [Google Scholar]
- Wang, L.; Han, T.; Zhan, X.S.; Wu, J.; Yan, H. Bipartite containment for linear multi-agent systems subject to unknown exogenous disturbances. Asian J. Control 2022, 24, 1836–1845. [Google Scholar] [CrossRef]
- Zuo, S.; Song, Y.L.; Lewis, F.; Davoudi, A. Bipartite output containment of general linear heterogeneous multi-agent systems on signed digraphs. IET Control Theory Appl. 2018, 12, 1180–1188. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, H.; Yu, L.; Sun, S. Cooperative bipartite containment control for heterogeneous networks with structurally balanced graph. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2885–2889. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, W.; Liang, H.; Basin, M.V.; Wang, B. Observer-based event-triggered fuzzy adaptive bipartite containment control of multiagent systems with input quantization. IEEE Trans. Fuzzy Syst. 2019, 29, 372–384. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, H.; Zhang, J.; He, Q. Distributed bipartite leader-following consensus of linear multi-agent systems with input time delay based on event-triggered transmission mechanism. ISA Trans. 2020, 100, 221–234. [Google Scholar] [CrossRef]
- Rahman, R.U.; Hammouch, Z.; Alsubaie, A.S.A.; Mahmoud, K.H.; Alshehri, A.; Az-Zo’bi, E.A.; Osman, M.S. Dynamical behavior of fractional nonlinear dispersive equation in Murnaghan’s rod materials. Results Phys. 2024, 56, 107207. [Google Scholar] [CrossRef]
- Di Paola, M.; Alotta, G.; Burlon, A.; Failla, G. A novel approach to nonlinear variable-order fractional viscoelasticity. Philos. Trans. R. Soc. A 2020, 378, 20190296. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Hassan, W.U.; Manzor, A.; Ahmed, S.; Niazi, A.U.K. Strengthening stability with centralized event-triggered control system with the disturbances and artificial time delay in wireless connected vehicle platooning (CVSs). Syst. Sci. Control Eng. 2024, 12, 2342818. [Google Scholar] [CrossRef]
- Wenlong, Y.; Ruiliang, D.; Weixian, Z.; Zongying, S.; Yisheng, Z. Fully Distributed Robust Adaptive Formation Control for Linear Multi-agent System with Uncertainties and Communication Delays. IFAC-PapersOnLine 2023, 56, 9227–9232. [Google Scholar] [CrossRef]
- Luo, L.; Mi, W.; Zhong, S. Adaptive consensus control of fractional multi-agent systems by distributed event-triggered strategy. Nonlinear Dyn. 2020, 100, 1327–1341. [Google Scholar] [CrossRef]
- Hua, Y.; Dong, X.; Li, Q.; Ren, Z. Distributed time-varying formation robust tracking for general linear multiagent systems with parameter uncertainties and external disturbances. IEEE Trans. Cybern. 2017, 47, 1959–1969. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Wu, M.; Yang, W.; Ji, J. A system decomposition method for region tracking control of a non-holonomic mobile robot with dynamic parameter uncertainties. Asian J. Control 2024, 26, 1459–1471. [Google Scholar] [CrossRef]
- Yang, R.; Liu, S.; Li, X. Observer-based bipartite containment control of fractional multi-agent systems with mixed delays. Inf. Sci. 2023, 626, 204–222. [Google Scholar] [CrossRef]
- Zhou, Y. Basic Theory of Fractional Differential Equations; World Scientific: Singapore, 2023. [Google Scholar]
- Sevinik Adigüzel, R.; Aksoy, Ã.; Karapinar, E.; Erhan, Ä.M. On the solution of a boundary value problem associated with a fractional differential equation. Math. Methods Appl. Sci. 2020. early view. [Google Scholar] [CrossRef]
- Huseynov, I.T.; Ahmadova, A.; Mahmudov, N.I. Fractional Leibniz integral rules for Riemann-Liouville and Caputo fractional derivatives and their applications. arXiv 2020, arXiv:2012.11360. [Google Scholar]
- Wen, Y.; Zhou, X.F.; Zhang, Z.; Liu, S. Lyapunov method for nonlinear fractional differential systems with delay. Nonlinear Dyn. 2015, 82, 1015–1025. [Google Scholar] [CrossRef]
- Arık, I.A.; Araz, S.I. Delay differential equations with fractional differential operators: Existence, uniqueness and applications to chaos. Commun. Anal. Mech. 2024, 16, 169–192. [Google Scholar] [CrossRef]
- Ye, Y.; Wei, H.; Lu, R.; Su, H.; Wu, Y. Containment control for networked fractional-order systems with sampled position data. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3881–3889. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, A.; Javeed, M.A.; Rehman, S.; Niazi, A.U.K.; Zhong, Y. Advanced Observation-Based Bipartite Containment Control of Fractional-Order Multi-Agent Systems Considering Hostile Environments, Nonlinear Delayed Dynamics, and Disturbance Compensation. Fractal Fract. 2024, 8, 473. https://doi.org/10.3390/fractalfract8080473
Khan A, Javeed MA, Rehman S, Niazi AUK, Zhong Y. Advanced Observation-Based Bipartite Containment Control of Fractional-Order Multi-Agent Systems Considering Hostile Environments, Nonlinear Delayed Dynamics, and Disturbance Compensation. Fractal and Fractional. 2024; 8(8):473. https://doi.org/10.3390/fractalfract8080473
Chicago/Turabian StyleKhan, Asad, Muhammad Awais Javeed, Saadia Rehman, Azmat Ullah Khan Niazi, and Yubin Zhong. 2024. "Advanced Observation-Based Bipartite Containment Control of Fractional-Order Multi-Agent Systems Considering Hostile Environments, Nonlinear Delayed Dynamics, and Disturbance Compensation" Fractal and Fractional 8, no. 8: 473. https://doi.org/10.3390/fractalfract8080473
APA StyleKhan, A., Javeed, M. A., Rehman, S., Niazi, A. U. K., & Zhong, Y. (2024). Advanced Observation-Based Bipartite Containment Control of Fractional-Order Multi-Agent Systems Considering Hostile Environments, Nonlinear Delayed Dynamics, and Disturbance Compensation. Fractal and Fractional, 8(8), 473. https://doi.org/10.3390/fractalfract8080473







