Adaptive Synchronization of Fractional-Order Uncertain Complex-Valued Competitive Neural Networks under the Non-Decomposition Method
Abstract
1. Introduction
- (1)
- A novel FOUCVCNNs model is proposed, and its dynamics have been analyzed based on non-decomposition method.
- (2)
- A new adaptive controller is designed to realize the synchronization of FOUCVCNNs.
- (3)
- By means of the fractional Lyapunov approach and the inequality technique, some effective synchronization results for FOUCVCNNs have been obtained, which can be further extended to deal with the dynamical study of integer-order one.
2. Model Description and Preliminaries
- (i)
- (ii)
- (iii)
- (iv)
3. Main Results
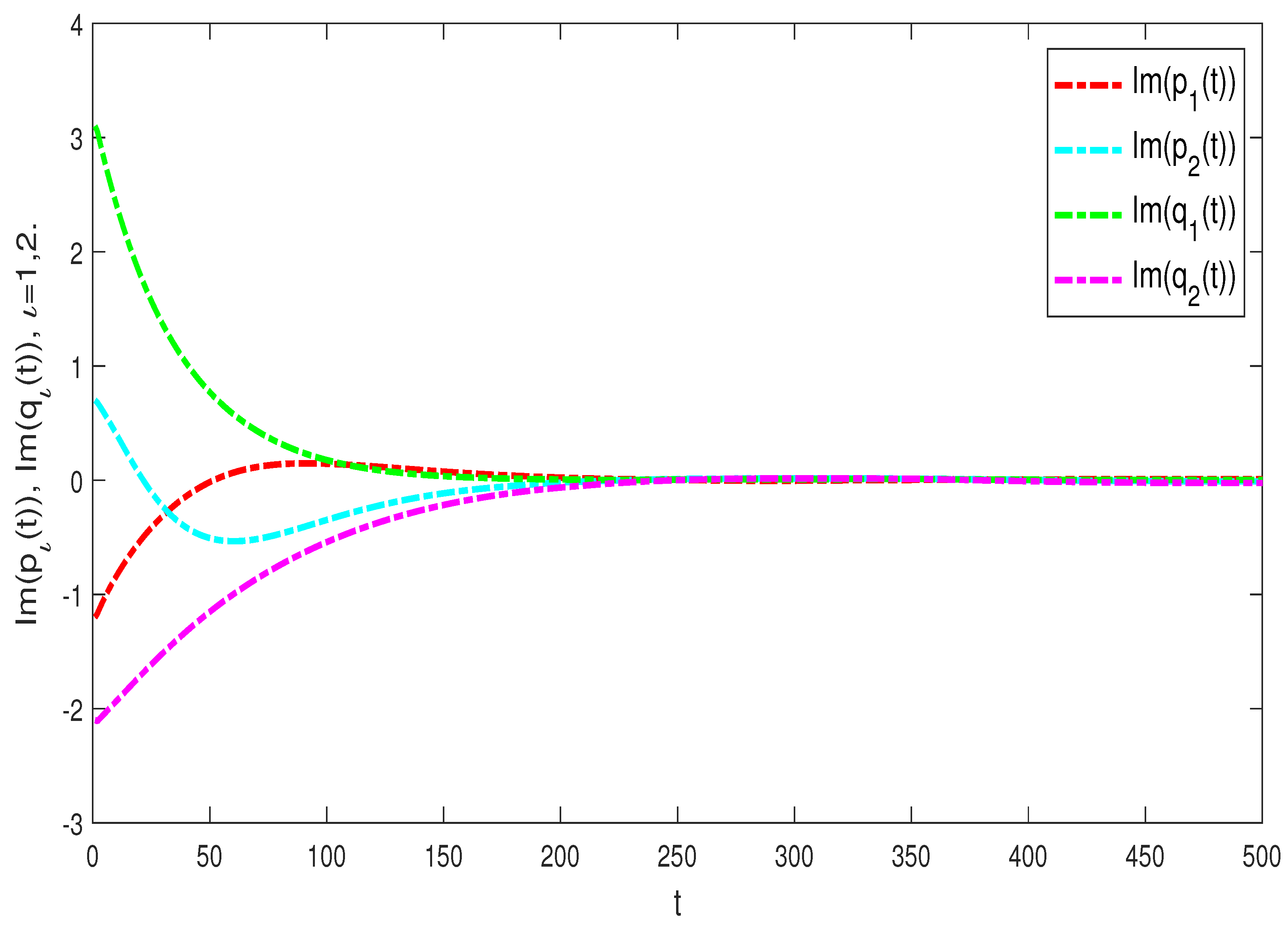
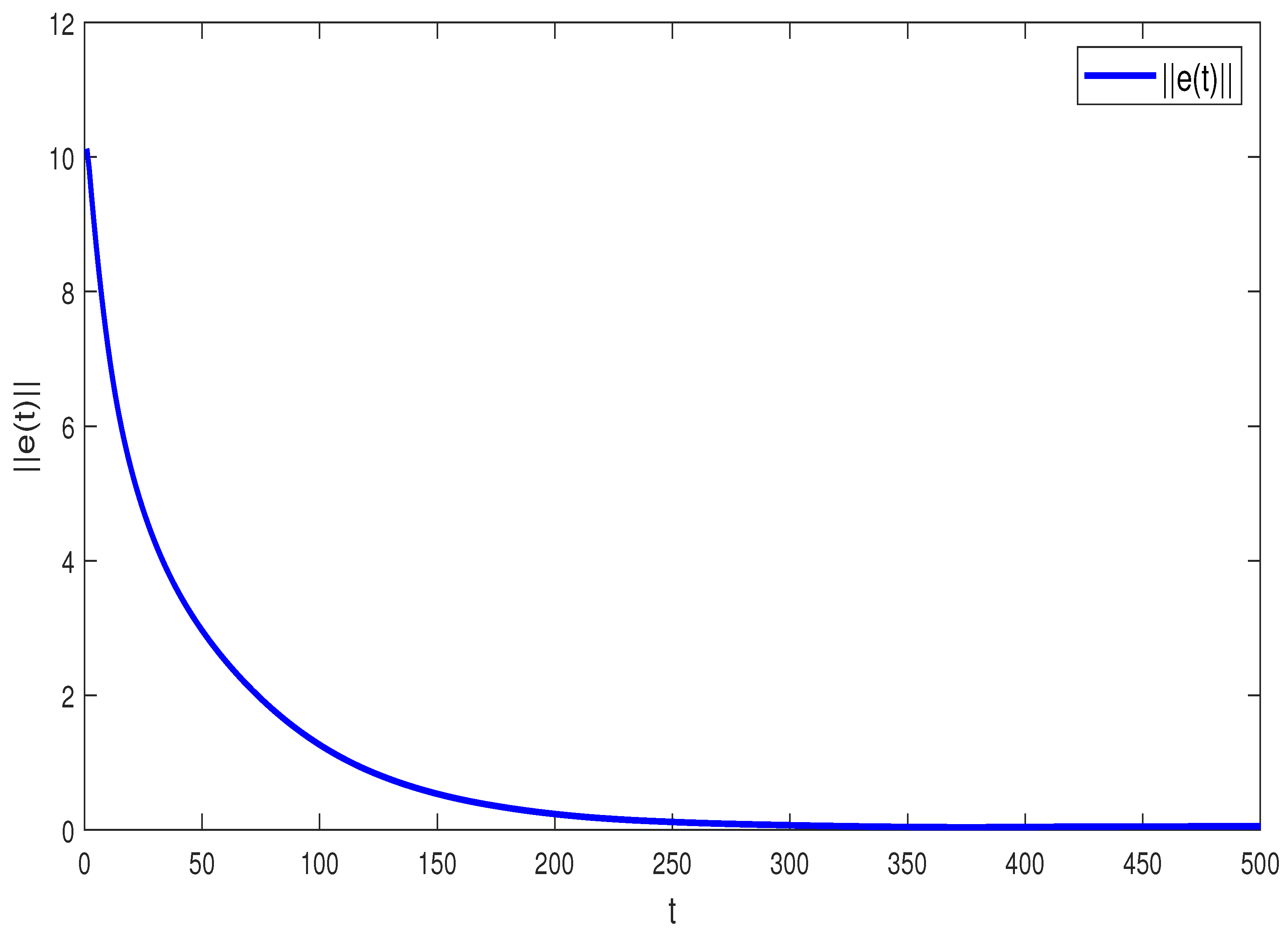
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Proof of Theorem 1
Appendix B. The Proof of Corollary 1
Appendix C. The Proof of Corollary 2
Appendix D. The Proof of Corollary 3
References
- Hu, M.; Huang, X.; Shi, Q.; Yuan, F. Design and analysis of a memristive Hopfield switching neural network and application to privacy protection. Nonlinear Dyn. 2024, 112, 12485–12505. [Google Scholar] [CrossRef]
- Cao, J.; Stamov, F.; Stamov, G.; Stamova, I. Impulsive controllers design for the practical stability analysis of gene regulatory networks with distributed delays. Fractal Fract. 2023, 7, 847. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, Z. Finite-time synchronization for delayed BAM neural networks by the approach of the same structural functions. Chaos Solitons Fractals 2022, 164, 112655. [Google Scholar] [CrossRef]
- Aili, A.; Chen, S.; Zhang, S. Event-triggered synchronization of coupled neural networks with reaction-diffusion terms. Mathematics 2024, 12, 1409. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, Q.; Huang, T. Global polynomial synchronization of proportional delayed inertial neural networks. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4487–4497. [Google Scholar]
- Wang, L.; Zhang, C. Exponential synchronization of memristor-based competitive neural networks with reaction-diffusions and infinite distributed delays. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 745–758. [Google Scholar] [CrossRef] [PubMed]
- Cohen, M.; Grossberg, S. Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans. Syst. Man Cybern. 1983, 13, 815–825. [Google Scholar] [CrossRef]
- Adhira, B.; Nagamani, G. Exponentially finite-time dissipative discrete state estimator for delayed competitive neural networks via semi-discretization approach. Chaos Solitons Fractals 2023, 176, 114162. [Google Scholar] [CrossRef]
- Xu, C.; Jiang, M.; Hu, J. Mean-square finite-time synchronization of stochastic competitive neural networks with infinite time-varying delays and reaction-diffusion terms. Commun. Nonlinear Sci. Numer. Simulat. 2023, 127, 107535. [Google Scholar] [CrossRef]
- Wang, L.; Tan, X.; Wang, Q.; Hu, J. Multiple finite-time synchronization and settling-time estimation of delayed competitive neural networks. Neurocomputing 2023, 552, 126555. [Google Scholar] [CrossRef]
- Yu, J.; Hu, C.; Jiang, H. Corrigendum to projective synchronization for fractional neural networks. Neural Netw. 2015, 67, 152–154. [Google Scholar] [CrossRef]
- Chen, S.; Li, H.; Wang, L.; Hu, C.; Jiang, H.; Li, Z. Finite-time adaptive synchronization of fractional-order delayed quaternion-valued fuzzy neural networks. Nonlinear Anal. Model. Control 2023, 28, 804–823. [Google Scholar] [CrossRef]
- Zhang, S.; Du, F.; Chen, D. New approach to quasi-synchronization of fractional-order delayed neural networks. Fractal Fract. 2023, 7, 825. [Google Scholar] [CrossRef]
- Li, H.; Hu, C.; Cao, J.; Jiang, H.; Alsaedi, A. Quasi-projective and complete synchronization of fractional-order complex-valued neural networks with time delays. Neural Netw. 2019, 118, 102–109. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Li, H.; Kao, Y.; Zhang, L.; Hu, C. Finite-time stabilization of fractional-order fuzzy quaternion-valued BAM neural networks via direct quaternion approach. J. Frankl. Inst. 2021, 358, 7650–7673. [Google Scholar] [CrossRef]
- Rajchakit, G.; Chanthorn, P.; Niezabitowski, M.; Raja, R.; Baleanu, D.; Pratap, A. Impulsive effects on stability and passivity analysis of memristor-based fractional-order competitive neural networks. Neurocomputing 2020, 417, 290–301. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, T.; Wu, Q.; Zeng, Z. Multistability of delayed fractional-order competitive neural networks. Neural Netw. 2021, 140, 325–335. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Yu, J.; Li, W.; Feng, J. Global asymptotic stability of fractional-order competitive neural networks with multiple time-varying-delay links. Appl. Math. Comput. 2021, 389, 125498. [Google Scholar] [CrossRef]
- Wu, Z.; Nie, X.; Cao, B. Coexistence and local stability of multiple equilibrium points for fractional-order state-dependent switched competitive neural networks with time-varying delays. Neural Netw. 2023, 160, 132–147. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Cao, J.; Rajchakit, G.; Fardoun, H. Stability and synchronization criteria for fractional order competitive neural networks with time delays: An asymptotic expansion of Mittag Leffler function. J. Frankl. Inst. 2019, 356, 2212–2239. [Google Scholar] [CrossRef]
- Gao, P.; Ye, R.; Zhang, H.; Stamova, I.; Cao, J. Asymptotic stability and quantitative synchronization of fractional competitive neural networks with multiple restrictions. Math. Comput. Simul. 2024, 217, 338–353. [Google Scholar] [CrossRef]
- Wang, S.; Jian, J. Predefined-time synchronization of incommensurate fractional-order competitive neural networks with time-varying delays. Chaos Solitons Fractals 2023, 177, 114216. [Google Scholar] [CrossRef]
- Yang, S.; Jiang, H.; Hu, C.; Yu, J. Synchronization for fractional-order reaction-diffusion competitive neural networks with leakage and discrete delays. Neurocomputing 2021, 436, 47–57. [Google Scholar] [CrossRef]
- Shafiya, M.; Nagamani, G.; Dafik, D. Global synchronization of uncertain fractional-order BAM neural networks with time delay via improved fractional-order integral inequality. Math. Comput. Simul. 2022, 191, 168–186. [Google Scholar] [CrossRef]
- Chen, S.; Yang, J.; Li, Z.; Li, H.; Hu, C. New results for dynamical analysis of fractional-order gene regulatory networks with time delay and uncertain parameters. Chaos Solitons Fractals 2023, 175, 114041. [Google Scholar] [CrossRef]
- Ali, M.S.; Hymavathi, M.; Kauser, S.; Rajchakit, G.; Hammachukiattikul, P.; Boonsatit, N. Synchronization of fractional order uncertain BAM competitive neural networks. Fractal Fract. 2022, 6, 14. [Google Scholar]
- Li, H.; Kao, Y.; Bao, H.; Chen, Y. Uniform stability of complex-valued neural networks of fractional order with linear impulses and fixed time delays. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5321–5331. [Google Scholar] [CrossRef] [PubMed]
- Panda, S.; Nagy, A.; Vijayakumar, V.; Hazarika, B. Stability analysis for complex-valued neural networks with fractional order. Chaos Solitons Fractals 2023, 175, 114045. [Google Scholar] [CrossRef]
- Xu, D.; Tan, M. Multistability of delayed complex-valued competitive neural networks with discontinuous non-monotonic piecewise nonlinear activation functions. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 352–377. [Google Scholar] [CrossRef]
- Zheng, B.; Hu, C.; Yu, J.; Jiang, H. Finite-time synchronization of fully complex-valued neural networks with fractional-order. Neurocomputing 2020, 373, 70–80. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, H.; Zhang, W.; Zhang, H. Quasi-projective synchronization for Caputo type fractional-order complex-valued neural networks with mixed delays. Int. J. Control Autom. 2022, 20, 1723–1734. [Google Scholar] [CrossRef]
- Xu, Y.; Li, H.; Yang, J.; Zhang, L. Quasi-projective synchronization of discrete-time fractional-order complex-valued BAM fuzzy neural networks via quantized control. Fractal Fract. 2024, 8, 263. [Google Scholar] [CrossRef]
- Chen, S.; Li, H.; Bao, H.; Zhang, L.; Jiang, H.; Li, Z. Global Mittag-Leffler stability and synchronization of discrete-time fractional-order delayed quaternion-valued neural networks. Neurocomputing 2022, 511, 290–298. [Google Scholar] [CrossRef]
- Hu, X.; Wang, L.; Zhang, C.; Wan, X.; He, Y. Fixed-time stabilization of discontinuous spatiotemporal neural networks with time-varying coefficients via aperiodically switching control. Sci. China Inf. Sci. 2023, 66, 152204. [Google Scholar] [CrossRef]
- Zhu, S.; Lü, J. Further on pinning synchronization of dynamical networks with coupling delay. SAIM J. Control Optim. 2024, 62, 1933–1952. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Application of Fractional Differential Equations; Elsevier: New York, NY, USA, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Xu, C.; Liao, M.; Wang, C.; Sun, J.; Lin, H. Memristive competitive hopfield neural network for image segmentation application. Cogn. Neurodynamics 2023, 17, 1061–1077. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, T.; Wu, A.; Zeng, Z. Mittag-Leffler stability and application of delayed fractional-order competitive neural networks. Neural Netw. 2024, 179, 106501. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Luo, X.; Yang, J.; Li, Z.; Li, H. Adaptive Synchronization of Fractional-Order Uncertain Complex-Valued Competitive Neural Networks under the Non-Decomposition Method. Fractal Fract. 2024, 8, 449. https://doi.org/10.3390/fractalfract8080449
Chen S, Luo X, Yang J, Li Z, Li H. Adaptive Synchronization of Fractional-Order Uncertain Complex-Valued Competitive Neural Networks under the Non-Decomposition Method. Fractal and Fractional. 2024; 8(8):449. https://doi.org/10.3390/fractalfract8080449
Chicago/Turabian StyleChen, Shenglong, Xupeng Luo, Jikai Yang, Zhiming Li, and Hongli Li. 2024. "Adaptive Synchronization of Fractional-Order Uncertain Complex-Valued Competitive Neural Networks under the Non-Decomposition Method" Fractal and Fractional 8, no. 8: 449. https://doi.org/10.3390/fractalfract8080449
APA StyleChen, S., Luo, X., Yang, J., Li, Z., & Li, H. (2024). Adaptive Synchronization of Fractional-Order Uncertain Complex-Valued Competitive Neural Networks under the Non-Decomposition Method. Fractal and Fractional, 8(8), 449. https://doi.org/10.3390/fractalfract8080449





